近似公式在航天测控中的应用
2016-08-12李晓勇王旭良袁小江
倪 兴,李晓勇,杨 磊,王旭良,袁小江
(中国卫星海上测控部,江苏 江阴 214431)
近似公式在航天测控中的应用
倪兴,李晓勇,杨磊,王旭良,袁小江
(中国卫星海上测控部,江苏 江阴214431)
摘要:航天测控中,需要避免过于复杂的运算过程,提高计算速度时,常常运用一些近似公式。分析了近似公式的作用、来源,以及在航天测控中的一些应用情况。提出了一种航天测量船实战使用的简化的大气折射修正公式,并对事后使用的精确公式进行了对比分析,结果表明,运用简化的大气折射修正公式处理后的数据在定轨精度上满足要求,同时满足了实时数据处理对计算速度的要求。
关键词:航天测控;近似公式;大气折射
本文引用格式:倪兴,李晓勇,杨磊,等.近似公式在航天测控中的应用[J].兵器装备工程学报,2016(6):174-176.
Citation format:NI Xing, LI Xiao-yong,YANG Lei, et al.Application of Approximate Formula on TT&C System[J].Journal of Ordnance Equipment Engineering,2016(6):174-176.
在航天测控中,尤其是在数据处理中,为了获取高精度的数据,一些数学模型和计算手段比较复杂,处理时间相对较长,但在实时的数据处理中,要求尽可能快地将数据处理完毕,需要避免过于繁复的运算过程,提高计算速度,因此在保证一定精度要求的前提下,应用一些近似公式。有时为了估算或预报某些参数,利用近似公式。
1 近似公式的来源
获取近似公式,大致有以下几种方法。
1.1Tailer公式
如果函数f(x)满足条件:① 在区间[a,b]上有定义;② 在此闭区间上有一直到n阶的连续导数f′(x),…,f(n)(x);③ 当a 式中 常用的由Tailer公式而来的近似公式有 这些公式中,x的值越小,则结果越精确。 1.2精确公式的简化 有些近似公式,是对计算条件做某种近似假设或将精确公式做适当化简,例如,在计算飞行目标的地面高度时,便需要假设地球是个球形,设地球半径为a,雷达的测量元素为R、E、A,由几何关系和余弦定理可得 (a+h)2=a2+R2-2aRcos(90°+E) 对于航天器入轨段或低轨航天器运行段,有h≪a,于是得近似公式 (1) 1.3经验公式 还有一部分近似公式是根据试验结果或观测数据拟合的经验公式,由于试验结果不可避免含有误差,因此与试验曲线对应的经验公式也都是近似公式。 例如,计算电波折射指数的史密斯—文特劳公式 (2) 便是一个经验公式。 经验公式不仅在工程运用上具有实用价值,而且在理论分析上具有一定的价值。建立经验公式的主要步骤是配置公式类型、决定公式中的系数、对公式进行检验3个过程。配置经验公式,并无一般的通用方法,其具体形式的确定,是根据理论的推断或从试验数据变化的趋势推测而来。常用的决定系数的方法有图解法、平均法、最小二乘法、相关分析法[2]。检验经验公式时,可将已测知的自变量的值代入函数中,看计算出的函数值与实测值相差多少,若误差太大,则需对经验公式适当修改。 近似公式在航天测控中有着广泛的应用,如用于数据处理、精度分析、实时计算等。 2.1数据处理 数据处理中应用的近似公式很多,如表示三维空间中的旋转矩阵 (3) 当旋转角度很小时,由Tailer公式sinα≈α、cosα≈1可得 (4) 其中A是一个反对称矩阵 (5) 这种极小旋转坐标变换公式在航天测控中是很多的,如地心固连坐标系与准地心固连坐标系之间的差别是极移的影响,这两个坐标系之间的转换矩阵为 (6) 由于极移量很小,于是其转换矩阵可写为 (7) 在数据处理中,有时候空间大地直角坐标与大地坐标需要互相转换,由大地坐标转换为大地直角坐标的公式是[3] (8) 式中,N,e2为卯酉圈曲率半径和参考椭球第一偏心率。 而由大地直角坐标转换为大地坐标的公式是 (9) 从上式的第二式可以知道,大地纬度B的计算公式是一个隐函数,不能直接求解,只能通过迭代法逐步求解。而由近似公式 (10) 式中 (11) (12) (13) (14) 则可以直接求得大地纬度B,经测算,当H<10 km时,公式的精度不低于0.000 01″,对一般数据处理而言,精度已足够。 2.2精度估计 我国大部分雷达设备是使用极坐标的单站定位体制,主要的测量元素为R、E、A,对陆站而言,其设备位置可以通过大地测量精确获得,并且固定不变,其定位精度就是测控设备的精度,而航天测量船在海上执行测控任务时是运动的,另外受风、浪、涌的影响,会产生船摇、变形,船载测控设备同样受此影响,因此,测量船的误差是测控设备、船摇、变形、船位误差的合成[4]。即 (15) 式中:σP为总误差;σPl为雷达位置误差;σPy为船摇位置误差;σPb为变形位置误差;σPw为船位位置误差。 测量船船位是由惯导系统实时获得的,精度较低,是海上测量的主要误差源之一。船位误差对目标误差的影响是一种平移偏倚误差,因地球曲率而被放大,可以用下面的近似公式估计[5] (16) 式中:d站址误差;D为站址误差引起的目标位置误差;Re为地球平均半径;h为目标高度。由式(1)可得 (17) 船摇姿态误差和船体变形误差可以等效成设备的方位和俯仰角误差,如果存在船体姿态误差Δkc,Δφc,Δθc,产生的测量设备方位和俯仰角等效误差为 (18) 于是有 (19) 若纵摇与横摇等精度测量,即σφc=σθc,由船摇引起的目标位置误差为 (20) 同样,由变形引起的目标位置误差为 (21) 雷达本身的目标位置误差为 (22) 将式(17)、式(20)、式(21)、式(22)代入式(15)便可得测量船定位精度的近似估计。 2.3实时计算 电波射线在真空中以光速传播,但在地球上空大气中传播时,由于空间各处大气成分、湿度、温度、密度和电离程度都不相同,介质特性也极其复杂,因此其传播速度发生了改变,轨迹也发生了弯曲,因此电波传播的路径是曲线,即发生了折射[6-8]。空间目标的定位是用光学或无线电方法确定其方位、仰角、距离,由于大气折射的影响,折射误差可以远大于设备本身的测量误差,因此,必须修正大气折射误差。常用的精度较高的大气折射修正有射线描迹法、高斯分层法,在航天测量船的实时数据处理中,对时间有严格的要求,如果要采用高斯分层法精确修正电波折射,随着精度的提高和观测仰角的不同,计算速度将会有所变化,无法满足实时处理对计算速度的要求,因此采用以下简化的电波折射误差修正公式。假设未修正折射误差的斜距和仰角分别为Re和Ee,而修正电波折射误差后的观测量分别为R和E,则电波折射误差修正量为 ΔR=0.007 16N0cotEe(h/(h+5 000m)) (23) ΔE=N0cotEe(h/(h+10 000 m))10-6 (24) 式中:h为目标离测站地面的高度;N0为测站地面的电波折射指数。 由式(23)、式(24)两式,则得到电波折射修正后的观测量为 R=Re-ΔR E=Ee-ΔE 而外测数据事后处理采用的大气折射修正为高斯分层法,较为复杂,感兴趣者可查阅相关资料。分别利用实时简化修正的处理数据和事后高斯分层修正的处理数据定轨,再与精轨做比较,结果如表1所示。 从统计结果看,事后高斯分层修正后的数据定轨精度略高,但在量级上两种方法大致相当,而简化大气折射修正满足实时处理对计算速度的要求,因而被广泛地使用在实时数据处理中。 表1 两种电波折射修正定轨结果与精轨差异结果统计 近似公式在航天测控中有着广泛的运用,可以根据实际工作的需要,导出具有一定精度的近似公式,给分析问题带来方便。 参考文献: [1]《数学手册》编写组.数学手册[M].北京:高等教育出版社,2009. [2]张普庆.经验公式的系数计算及类型配置[J].山东师大学报:自然科学版,1987,2(2):158-165. [3]严莘稼,曾启雄.空间大地直角坐标直接结算大地纬度的近似公式[J].北京建筑工程学院学报,1991(2):55-58. [4]倪兴,李晓勇,薛国虎,等.测量船姿态误差影响分析[J].四川兵工学报,2014,35(5):149-151. [5]简仕龙,费加兵,刘冰,等.航天测量船海上测控技术概论[M].北京:国防工业出版社,2009. [6]刘利生,张玉祥,李杰,等.外弹道测量数据处理[M].北京:国防工业出版社,2002. [7]李辉芬,席震东,薛国虎,等.低仰角大气折射误差对初轨精度的影响分析[J].飞行器测控学报,2012,31(3):54-57. [8]张瑜,张洁寒.全国大气折射率剖面预测方法[J].电光与控制,2011,18(7):46-48. (责任编辑杨继森) doi:10.11809/scbgxb2016.06.041 收稿日期:2015-12-25;修回日期:2016-01-15 作者简介:倪兴(1976—),男,工程师,主要从事海上测量数据处理与精度分析研究。 中图分类号:TJ01;V557 文献标识码:A 文章编号:2096-2304(2016)06-0174-03 Application of Approximate Formula on TT&C System NI Xing, LI Xiao-yong,YANG Lei, WANG Xu-liang, YUAN Xiao-jiang (China Satellite Maritime Tracking and Controling Department, Jiangyin 214431, China) Abstract:The approximate formula is often adopted to enhance the computation speed and avoid the complicated calculation. We briefly discussed the source and applications of the related approximate formulae in space-tracking engineering. At last, a new method of a simplified formula about atmospheric refraction correction used on TT&C ship was proposed, and then we compared it with an accurate formula used on accurate handling. The result shows that the accuracy of initial orbit based on simplified formula is satisfied and the speed of compute is satisfied. Key words:spaceflight test control; approximate formula; atmospheric refraction2 近似公式在航天测控中的应用
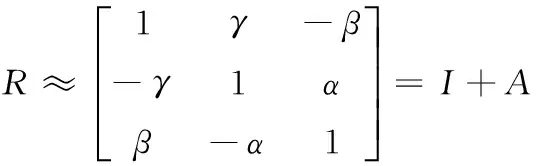


3 结束语
