光电跟踪系统前馈速度求解方法
2016-08-12刘启辉董琦昕
文 云,刘启辉,董琦昕
(中国兵器工业第五八研究所,四川 绵阳 621000)
光电跟踪系统前馈速度求解方法
文云,刘启辉,董琦昕
(中国兵器工业第五八研究所,四川 绵阳621000)
摘要:针对脱靶量滞后引起系统误差导致光电跟踪系统不能准确测距的问题,提出了加入前馈速度提高跟踪系统无差度的复合控制策略;以等效正弦和目标模拟航路为仿真模型,通过基于最小二乘的多项拟合算法对目标航迹实时预测以及跟踪微分器或差分低通滤波器求解目标前馈速度,对前馈速度求解算法进行了软件仿真,仿真结果表明:航迹误差与前馈速度误差均满足实际系统要求;将此算法应用于某型光电跟踪系统,在外场试验中对特定目标的稳定最大跟踪误差在0.4 m以内。
关键词:脱靶量滞后;复合控制;前馈速度;模拟航路;多项拟合;跟踪微分器
本文引用格式:文云,刘启辉,董琦昕.光电跟踪系统前馈速度求解方法[J].兵器装备工程学报,2016(6):29-34.
Citationformat:WENYun,LIUQi-hui,DONGQi-xin.SolvingMethodofFeedForwardVelocityinPhotoelectricTrackingSystem[J].JournalofOrdnanceEquipmentEngineering,2016(6):29-34.
在光电跟踪系统中,图像处理分系统提取红外图像中目标偏离视场中心的偏差量(脱靶量)作为伺服跟踪分系统的控制输入[1],实现对目标的闭环跟踪。由于红外探头图像生成、图像传输、图像处理板目标提取和脱靶量输出过程均不可避免的消耗时间,导致伺服跟踪分系统的目标反馈输入滞后于实际目标位置,表现为目标在视场内产生脱靶量系统误差。脱靶量滞后时间越长,目标的机动性越强,系统误差越大[2]。当脱靶量较大时,光电跟踪系统的激光测距设备将无法照射目标产生回波输出目标距离信息,不能将目标从转台极坐标系转换到炮塔直角坐标系下实现“光电带炮”目标打击。李亚宁等[3-4]基于多项式拟合算法对空中目标进行了预测,取得较好的效果,但未将该算法应用于实际跟踪系统中。本文以光电跟踪控制系统为研究对象,将目标预测和系统跟踪相结合进行了研究。
1 复合控制
为提高系统的无差度,伺服跟踪系统采用复合控制策略[5],其原理图如图1。Gv(s)为速度闭环传递函数,Cp(s)为位置环校正器,Gf(s)为前馈传递函数。
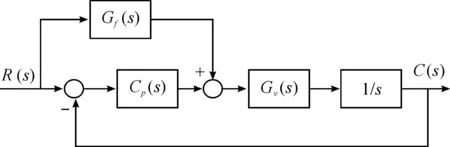
图1 复合控制原理图
无前馈时,跟踪系统的开环传递函数为
(1)
加入前馈后,系统的闭环传递函数为
(2)
其等效开环传递函数为
(3)
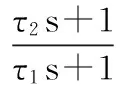
(4)
此时系统为I型系统,仅能实现位置无差。加入前馈速度后Gf(s)=s,代入式(2)和(3)得到系统的等效开环传递函数为
(5)
系统变为II型系统,位置和速度误差均为零,由此可见,加入前馈速度能在保证系统稳定性前提下提高系统的无差度,消除速度误差提高伺服系统跟踪精度。前馈函数同时加入加速度时,可将系统变为III型系统,实现加速度误差,但由于测量和过程噪声的影响使加速度精度较低,不能保持系统稳定,因此工程中通常加入前馈速度作为复合控制输入。
2 目标仿真模型
机动目标模型要求能充分反映运动目标的机动特征,常见的数学模型有导数多项式模型、辛格模型和当前统计模型等,导数多项式模型根据多项式在有限区间可以任意精度逼近一个连续函数,模拟目标航迹;辛格模型以二阶导数多项式模型进行改进,假定目标机动加速度概率密度函数呈均匀分布,且机动加速度均值为零;当前统计模型以辛格模型进行改进,认为目标以某加速度运动时,下一时刻加速度在当前加速度值的某一领域内[6]。本文根据某型光电跟踪系统的主要跟踪目标为研究对象分别建立了等效正弦模型和模拟航路模型。
2.1等效正弦模型
根据运动目标的机动特性,采用速度为20°/s,加速度为20°/s2的等效正弦曲线,工程中采用密位(m)单位,得到位置正弦曲线为Y=333.4sint,如图2所示。
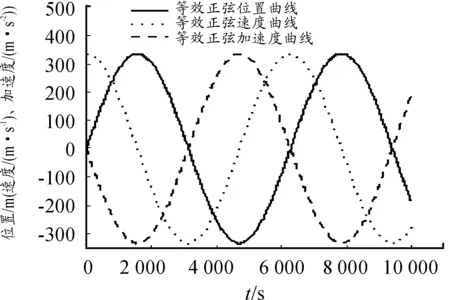
图2 等效正弦模型
2.2模拟航路模型
如图3所示为目标模拟航路示意图,目标由8km外的空域匀速飞行,飞行高度h=300m,飞行速度v=230m/s,航路捷径为x=250m,根据航迹解算,得到目标在转台极坐标系下的位置和速度公式:
(6)
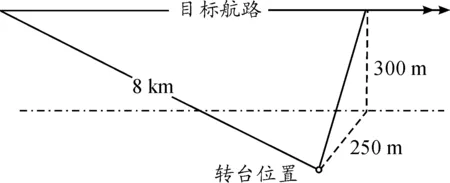
图3 目标模拟航路
得到转台坐标系下方位和俯仰轴的目标位置和速度曲线分别如图4所示。
3 航迹预测与速度求解
实时预测算法主要有最小二乘递推法、维纳滤波法和卡尔曼滤波算法等[7-8],最小二乘法是经典的参数估计方法,在许多算法中起主导作用[9],考虑到算法计算量和实时性要求,本文采用限定记忆型最小二乘递推算法,在选择预测模型时,采用多项式拟合模型逼近航迹序列,并对算法和实际运算进行优化和简化,以提高预测的精度。

图4 模拟航路航迹
3.1航迹预测
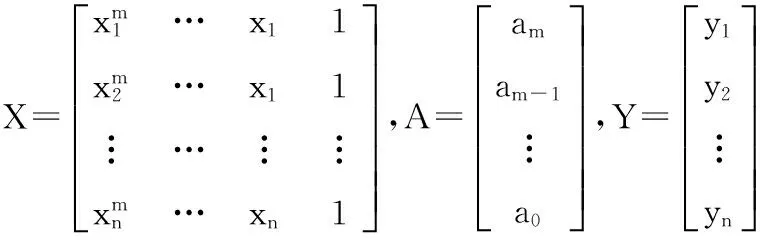
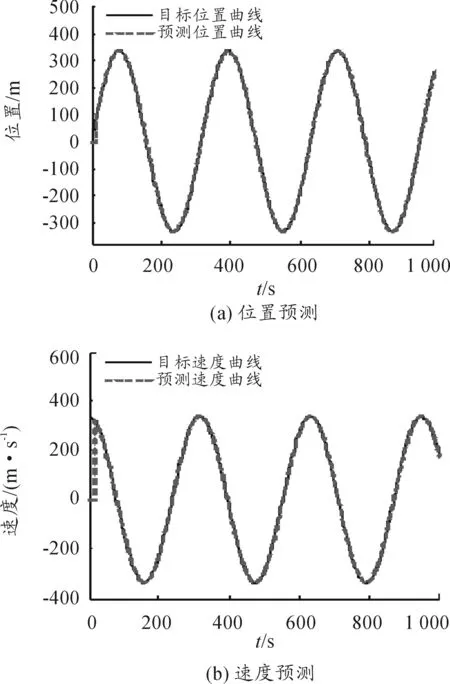
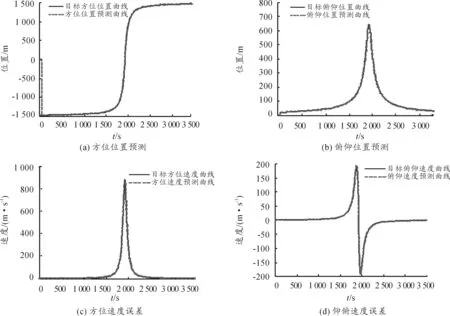
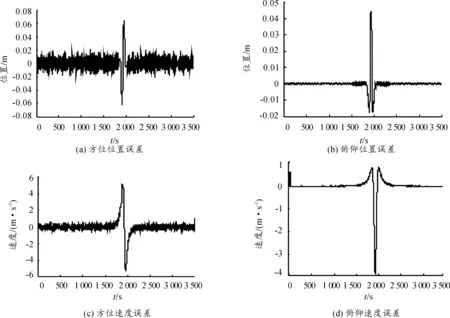
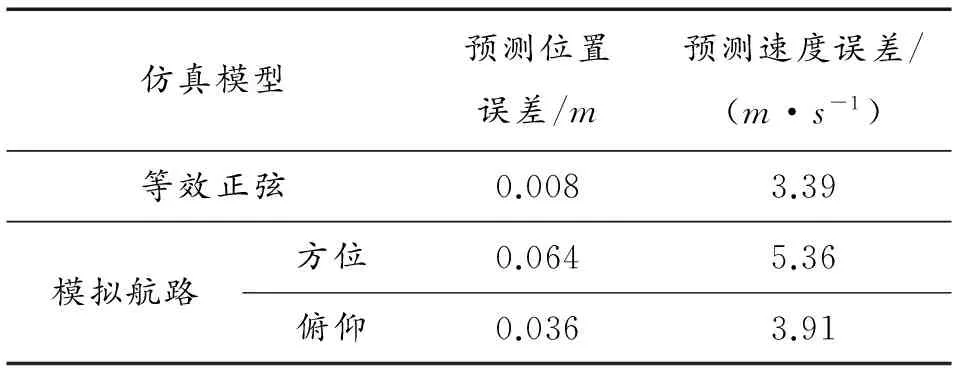
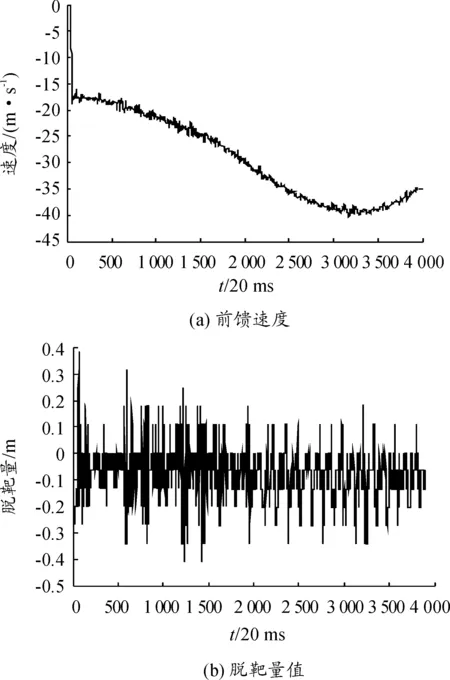
设有n个序列点(xi,yi)(i=1,2,…,n),存在一个m(m (7) 设Ri(i=1,2,…,n)为多项式P(x)与yi(i=1,2,…,n)的差值,有: (8) 即是 (9) 曲线P(x)并非通过所有序列点(xi,yi),故Ri(i=1,2,…,n)不全为零。最小二乘法就是选择aj(j=1,2,…,m),使σ有最小值,其中: (10) 式(10)的解可以用矩阵XA=Y的解来表示,其中: A=W-1XTY (11) 3.2前馈速度求解 多项式预测算法得到目标航迹后,目标的前馈速度可以通过跟踪微分器或对位置数据进行差分求解出目标前馈速度。采用跟踪微分器时,设Gc(s)为位置环校正器,Gv(s)为速度闭环传递函数,得到跟踪微分系统输入输出系统框图如图5,求得系统的闭环传递函数为 (12) 图5 跟踪微分器系统框图 采用位置数据差分求解前馈速度时,差分放大过程含有较大的过程噪声,通过采用低通滤波器对速度数据进行滤波[11],选择低通带宽较高时,不能有效滤除速度噪声,选择低通带宽较低时,会带来严重滞后,加大速度误差,脱靶量输出的帧频为50Hz,这里选择带宽为10rad/s求取低通后的前馈速度。数据处理低通滤波器采用“tustin”法离散化,得到离散方程为 (13) 光电跟踪系统的红外探头工作频率为50Hz,加上图像传输、图像处理和脱靶量输出消耗的时间,这里假定脱靶量滞后时间为40ms。 4.1等效正弦仿真 以速度为20°/s,加速度为20°/s2的等效正弦曲线为仿真模型,采用多项拟合预测算法得到位置和速度预测曲线如图6所示,预测航路在300ms后建航成功,开始输出预测曲线。 将目标位置和速度曲线与预测位置和预测速度曲线作差,得到等效正弦仿真模型的位置和速度误差曲线如图7所示。 从位置和速度误差曲线知,等效正弦仿真模型下预测位置与目标实际位置最大误差为8.38×10-3m,预测速度与目标实际速度最大误差为3.39m/s。 图6 等效正弦位置和速度预测 4.2模拟航路仿真 以2.2节模拟航路作仿真模型,分别得到方位和俯仰轴的位置和速度预测曲线如图8所示。 将目标位置和速度曲线与预测位置和预测速度曲线作差,分别得到模拟航路仿真模型的位置和速度误差曲线如图9所示。 图8 模拟航路位置和速度预测 图9 模拟航路位置和速度预测误差 从位置和速度误差曲线知,模拟航路模型下方位轴预测位置与目标实际位置最大位置误差为0.064,预测速度与目标实际速度的最大速度误差为5.36m/s;俯仰轴预测位置与目标实际位置最大位置误差为0.036m,预测速度与目标实际速度的最大速度误差为3.91m/s。 采用等效正弦和模拟航路进行仿真,得到仿真结果如表1所示。而红外探头视场大小为50m×37.5m,由此可见通过多项拟合法预测目标航迹输出前馈速度的算法精度可靠,可以用于实际工程中。 表1 仿真结果 4.2算法实现 将本文的目标航迹预测和前馈速度求解算法应用于某型光电跟踪系统,外场试验以某机动目标为对象,进行实时跟踪。记录前馈速度曲线和脱靶量数据曲线如图10所示,表明当目标运动速度不大于40m/s时,最大跟踪误差能保持在0.4m以内,跟踪误差均方差为0.095m。 图10 跟踪试验数据 求解过程中,采用多项拟合目标航迹预测加跟踪微分器(或差分低通)的方法得到前馈速度,并以等效正弦和模拟航路为模型进行了Matlab软件仿真,结果表明预测精度可靠。将该算法应用于实际系统中,通过外场试验检验,取得了良好的跟踪效果。 参考文献: [1]徐庆飞,张新,李卫民.二维空间中目标轨迹预测算法研究与分析[J].航空电子技术,2012,43(1):10-14. [2]安凯,马佳光,傅承毓.运动目标位置预测模型[J].系统工程与电子技术,2001(12):4-7. [3]李亚宁.基于多项式拟合法的空中目标实时位置预测研究[J].计算机与数字工程,2015,43(3):404-407. [4]徐智勇,傅承毓,王满意,等.用拟合函数法准确预测运动目标的轨迹[J].光电工程,2000,27(1):17-19. [5]陈明俊,李长红,杨燕.武器伺服系统工程实践[M].北京:国防工业出版社,2013:62-65. [6]李文军.复合轴光电跟踪系统控制策略的研究[D].长春:中国科学院长春精密机械与物理研究所,2006. [7]徐庆飞,张新,李卫民.二维空间中目标轨迹与测算法研究与分析[J].航空电子技术,2012(1):33-37. [8]杨晨,袁博,杨军,等.目标飞行航迹预测算法研究[J].弹箭与制导学报,2005,25(3):215-217. [9]张尚剑,刘永智.用滑动窗多项式拟合法实时预测运动目标轨迹[J].光电工程,2003,30(4):24-27. [10]邵伟,孟秋池,龚丹丹.多传感器数据融合与航迹预测[J].数学的实践与认识,2010,40(15):151-159. [11]黄知涛,郑龙席.高性能数据采集系统中信号的低通滤波原理及实践[J].测控技术,1999,18(5):55-56. [12]李璀,张钊,周勇.当前统计模型下的目标状态鲁棒H∞预估算法[J].兵工自动化,2014(9):83-85. (责任编辑周江川) doi:10.11809/scbgxb2016.06.007 收稿日期:2015-12-01;修回日期:2016-01-06 作者简介:文云(1987—),男,硕士,工程师,主要从事伺服稳定跟踪控制研究。 中图分类号:TN510 文献标识码:A 文章编号:2096-2304(2016)06-0029-06 SolvingMethodofFeedForwardVelocityinPhotoelectricTrackingSystem WENYun,LIUQi-hui,DONGQi-xin (No.58ResearchInstituteofChinaOrdnanceIndustries,Mianyang621000,China) Abstract:Aiming at the problem that photoelectric tracking system can’t measure distance accurately because of the system error caused by miss distance delay, the strategy of combined control based on feed forward velocity to raise the indiscrimination degree was proposed. This paper took equivalent sine and simulated route as models, and put forward polynomial fitting that based on least square to predict target trajectory in real time and solved feed forward velocity by tracking differentiator or differential and low-pass filter. Then a software simulation has done, and the results show that the trajectory and feed forward velocity error satisfies requirement in actual system. Takes the algorithm in a photoelectric tracking system, the maximum tracking error of field test is within 0.4 mils. Key words:miss distance delay; combined control; feed forward velocity; simulated route; polynomial fitting; tracking differentiator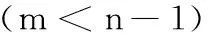

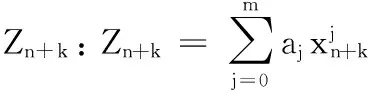

4 仿真与应用
5 结束语
