借助拉格朗日乘数法优化社会扩大再生产

■陶为群

借助拉格朗日乘数法优化社会扩大再生产

■陶为群

文章提出一种借助拉格朗日乘数法优化两大部类社会扩大再生产的方法。运用拉格朗日函数法，将获得扩大再生产的最优解析解问题，转化成目标函数在定义域边界点上的若干取值比较和判定问题，使问题变得很简单、明确。进而容易地确定扩大再生产的最优解所处的边界点，获得最优解。借助马克思《资本论》中的一个举例，对此方法做了计算验证。

扩大再生产；优化；拉格朗日乘数法；边界点；最优解

最优化是经济学的基本思想。马克思的社会扩大再生产的优化，是指对于马克思的社会扩大再生产公式获得最优解。研究解决社会扩大再生产的优化问题，对于深化马克思社会再生产理论以及对现实经济宏观调控的指导，都具有重要的理论意义。虽然已经有研究运用价值系数法和图解法解决了马克思的社会扩大再生产的优化问题（陶为群、陶川，2013；陶为群，2015），［1-2］但是这些数学方法在经济学当中还没有被比较普遍运用。鉴于此，本文提出借助在经济学当中比较普遍运用的拉格朗日乘数法，来优化马克思的社会扩大再生产。通过运用拉格朗日函数法，［3］可

以判定扩大再生产的目标函数最优值只能够在定义域边界点上取得，从而将获得扩大再生产的最优解析解问题转化成目标函数在定义域边界点上的一些取值比较和判定问题，进而较容易地确定扩大再生产的最优解所处的边界点，获得最优解。

一、马克思的社会扩大再生产优化的约束条件和目标函数

按照马克思社会再生产理论，社会生产部门划分成生产资料、消费资料的两个部类，分别记为第Ⅰ、Ⅱ部类。第j部类（j=Ⅰ，Ⅱ。下同）在t年初时点的总资本分解成用于购买生产资料的不变资本、购买劳动力的可变资本两个部分，分别记为都是每年周转一次；当年作为中间消耗转移到产品当中在产品当中新创造出来，并带来它的剩余价值。第j部类产品当中消耗的不变资本对于可变资本的固定不变倍数hj表示该部类的资本有机构成。剩余价值与可变资本之间保持固定不变的比率，以ej表示，是第j部类的剩余价值率。以分别表示第j部类的新创造价值、总产值，对确定了含义的字母前面加符号Δ表示在当年再生产过程中所形成的增量，以表示第j部类企业所有者把本部类的剩余价值中用于个人消费的部分。那么，社会再生产公式中有剩余价值使用的行为方程：

根据每个部类不变资本与可变资本的比例固定不变，从式（1）可以得到:

根据式（2）确定社会再生产对于待定变量有约束条件：

和

已经有研究用“图解法”证明了扩大再生产的充分必要条件是：

并且根据政治经济学教科书中指出的社会再生产的生产资料、消费资料实现条件，获得社会再生产的资本积累均衡方程：［4］

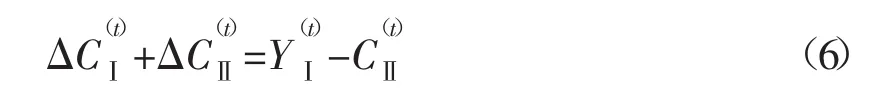
扩大再生产的最一般结果就是有新增的社会产品。由于每个部类所生产的新增的社会产品的价值构成是固定不变的，所以本部类新增的社会产品中的任何一个部分，都能够一般地代表整个新增的社会产品。为了便于和现代经济模型中的产品或者产出概念衔接，这里以第j部类新增的新创造价值（产品）一般地代表该部类新增的社会产品也就是产出。那么，下一年相对于本年两个部类新增的产出总和△Y（t）是：

ΔY（t）能够最一般地表示扩大再生产的结果。根据每个部类的新创造价值与不变资本之间的比例固定不变，有:

把式（8）代入式（7），得到：

新增的新创造价值（产品）总和ΔY（t）是待定变量的函数，它的定义域由式（2）、式

（3）、式（4）、式（6）和式（5）所确定。前面的分析已经说明，优化社会扩大再生产就是选取两个部类积累的一个匹配，使新增的新创造价值（产品）总和ΔY（t）取得最大值。那么，可以把式（9）所表示的ΔY（t）取得最大值作为扩大再生产的目标函数。式（2）、式（3）、式（4）、式（6）和式（5）就是待定变量的约束条件。所以扩大再生产的优化问题是有约束条件的函数最大值问题。

二、借助拉格朗日乘数法转化求函数的最大值问题

待定变量的约束条件式（3）、式（4）、式（6）和式（5）表明，待定变量的定义域是有界的。根据有界定义域的函数的最大值理论，如函数最大值存在，只能够在定义域内的极大值点或者在定义域的边界点上取得。而拉格朗日乘数法是确定函数有无有极大值点的有效方法。因此，使用目标函数式（9）和等式约束条件式（2）与式（6），构造如下拉格朗日函数λ3）。［3］

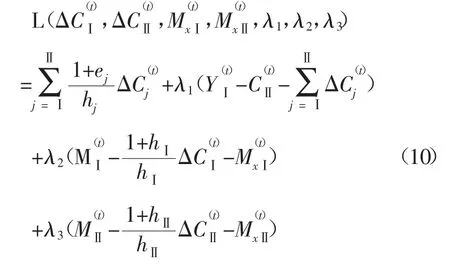
目标函数式（9）的极大值点必定是拉格朗日函数的驻点，也就是对于其中变量的偏导数函数数值为零的点，所以将拉格朗日函数对于其中的各个变量分别求偏导数并令其等于零。即：

由式（10）和式（11）得到：

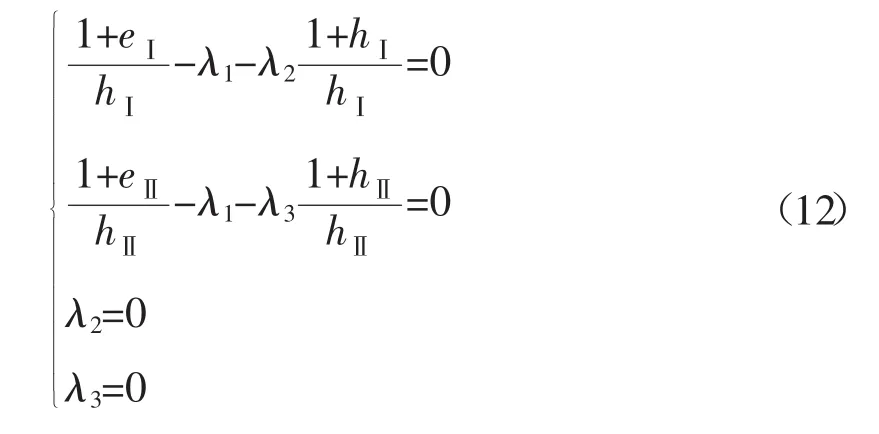
根据每个部类的新创造价值与不变资本之间的固定比例关系，第j部类的不变资本产出率是（1+ej）/hj。只要两个部类的不变资本产出率不相同即（1+eⅠ）/hⅠ≠（1+eⅡ）/hⅡ，式（12）就是一个矛盾方程组，不存在满足方程组的拉格朗日乘数λ1。所以拉格朗日函数没有驻点，从而目标函数式（9）也就没有极大值。于是，如果目标函数式（9）有最大值，就只能在定义域的边界点上取得。至此，就借助拉格朗日乘数法，把目标函数式（9）的最大值问题，转化成目标函数在定义域边界点上的若干取值的比较和判定问题，变得很简单、明确。

三、确定扩大再生产的最优解所处的边界点

只要两个部类的不变资本产出率不相同，就能够区别它们不变资本产出率大小比较的两种不同情形，分别确定在目标函数式（9）在定义域边界点上取得最大值。

在第Ⅰ部类的不变资本产出率高即（1+eⅠ）/ hⅠ＞（1+eⅡ）/hⅡ情形下，根据约束条件式（6），可以把目标函数式（9）变换成：

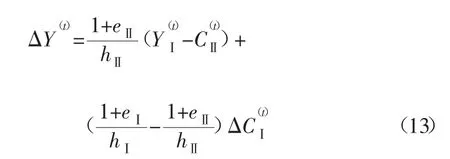
根据式（2）、式（3）、式（4）和式（6），在式（13）中变量取最小值或者最大值就是目标函数

比较式（13）和式（14）容易确定，式（14）确实是式（13）的最大值。所以，目标函数式（9）在边界点上取得最大值。而根据约束条件式（3）和式（6），能够确定：

其中

将式（15）和式（16）代入式（14）以及等式约束条件式（6）和式（2），可以在第Ⅰ部类的不变资本产出率高情形下，区分状态变量数在约束条件式（5）下处于两个不同的区间段时，扩大再生产的最优解所处的边界点和目标函数最大值。

目标函数最大值是:

时，最优解所处的边界点是:

目标函数最大值是:

同样道理，在第Ⅱ部类的不变资本产出率高即（1+eⅠ）/hⅠ＜（1+eⅡ）/hⅡ情形下，在目标函数式（13）中只有变量取最小值，目标函数可能取得最大值。

目标函数最大值是:

目标函数最大值是：

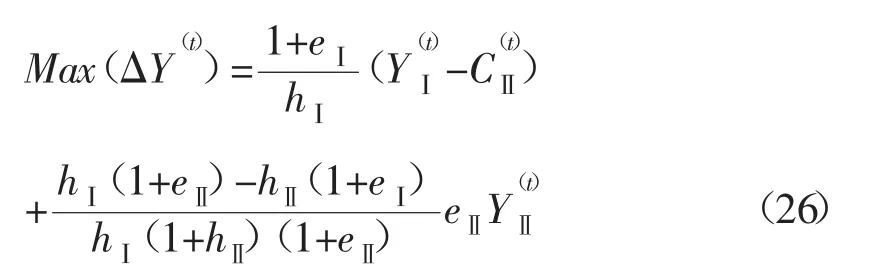
至此，优化扩大再生产问题获得解决。以上借助拉格朗日乘数法获得的社会扩大再生产的最优解，与运用“图解法”获得的最优解完全相同。［2］

四、借助《资本论》中的举例计算验证最优解

下面引用和借鉴马克思《资本论》第二卷第二十一章中的第二例验证社会扩大再生产的最优解。该例对应的条件是，目标函数中第Ⅰ部类的不变资本产出率高即（1+eⅠ）/hⅠ＞（1+eⅡ）/hⅡ。直接引用该例中的第2年（起始年份的下1年）数据，作为一般情形的扩大再生产。［4］此年份状态参数处于的区间是将此年份的有关具体数据代入式（17）、式（18），就计算出最优解所处的边界点和目标函数最大值数值。列在表1。

表1 借助《资本论》第二卷第二十一章中第二例的计算验证最优解

综合本文的全部论析以及算例验证，说明可以借助朗日函数法，判定扩大再生产的目标函数最优值只能够在定义域边界点上取得，从而将获得扩大再生产的最优解析解问题转化成目标函数在定义域边界点上的一些取值比较和判定问

题，变得很简单、明确。进而容易地确定扩大再生产的所处的边界点和目标函数最大值。

［1］陶为群，陶川.两大部类扩大再生产中的广义拉格朗日乘子［J］.经济数学，2013，30（4）.

［2］陶为群.马克思的社会扩大再生产优化的图解法［J］.创新，2015（6）.

［3］霍伊，利弗诺，麦克纳，等.经济数学（第二版）［M］.北京:中国人民大学出版社，2006：441-449.

［4］马克思.资本论：第2卷［M］.北京：人民出版社，2014：579-585.

［责任编辑：杨 彧］

The Optimization of the Social Expanded Reproduction with the Help of Lagrange Multiplier Method

Tao Weiqun

The paper presented a m ethod of optim ization of the tw o-sector social expanded reproduction w ith the help of Lagrange M ultiplier m ethod. B y use of Lagrange M ultiplier m ethod， a problem of getting optim al solution to the expanded reproduction w as converted to a problem of com paring and deciding several values of an objective function only at several frontier points of its definition， so that the problem becom es very sim ple and explicit. A nd then both of the frontier points w here are just the optim al solution to the expanded reproduction and the optim al solutions them selves w ere determ ined. A n exam ple from M arx's "D as kapital" w as draw n upon to verify the m ethod in a calculative w ay.

E xpanded R eproduction； O ptim ization； Lagrange M ultiplier M ethod； Frontier Point；O ptim al Solution

F091.91

A

1673-8616（2016）04-0033-06

2015-12-14

国家社科基金后期资助项目“马克思社会再生产理论深化与拓展的数理分析”（15FJL008）

陶为群，中国人民银行南京分行研究员、安徽财经大学兼职教授（江苏南京，210004）。