相参海杂波建模与建模和仿真研究
2016-08-11苟川杰何方敏
高 鑫,苟川杰,张 磊,何方敏
(海军工程大学,武汉430033)
相参海杂波建模与建模和仿真研究
高鑫,苟川杰,张磊,何方敏
(海军工程大学,武汉430033)
本文采用零记忆非线性变换法和球不变随机过程法对海杂波进行了建模和仿真研究,实现了相参Rayleigh分布、相参Weibull分布和相参K分布杂波的模拟,并对建模和仿真数据进行了检验,验证了建模和仿真方法的有效性。本次建模的特色之处在于考虑了杂波的相参性,并建立了三种杂波的概率分布模型和功率谱模型。
海杂波相参零记忆非线性变换法球不变随机过程法
0引言
随着探测水平、建模和仿真技术的发展,人们对海杂波的了解越来越深入。海杂波属于一种环境噪声,存在会严重影响舰船的电磁环境。最早研究者们常采用Rayleigh分布模型来描述产生的起伏属于均匀分布的海面杂波,但在分析高雷达分辨率的实验数据后发现,海面杂波的分布经常是非Rayleigh型的,所以相参对数正态分布和相参Weibull分布的统计模型被提出,但是这些模型并没有真正考虑到杂波在时间和空间上的相参性。为了更好的模拟海面杂波,一些新的杂波模型被不断提出[1]。近年来,任双桥做了更深入的研究,推导出了相参K分布海杂波的高阶自相关函数以及相参Guass序列与广义相参K分布序列的相关函数间的非线性关系,并采用ZMNL法对广义相参K分布杂波进行建模和仿真,求出了广义相参K分布序列。本文研究了海面杂波的概率分布模型和功率谱分布特征[2],对杂波进行了建模和仿真研究,实现了相参Rayleigh分布、相参Weibull分布和相参K分布杂波的建模和仿真并分析了各自优缺点。
1海面噪声的建模和仿真方法
1.1球不变随机过程法
球不变随机过程法(SIRP)的基本思路[6]是:先产生一个随机的相参Gauss序列,然后用所需的条件特征进行调制。SIRP的原理框图如下:
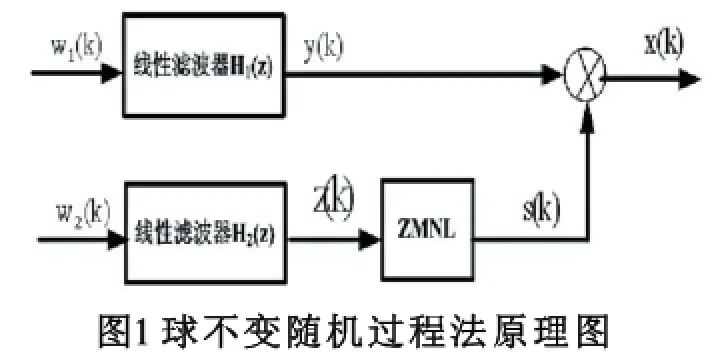
1.2零记忆非线性变换法
基于ZMNL法[12]产生满足条件的随机变量的步骤如下:先产生Guass白噪声序列再通过一个线性的数字滤波器H(z)可以得到序列,然后经过ZMNL得到通过研究ZMNL输入和输出的相参函数和的关系:
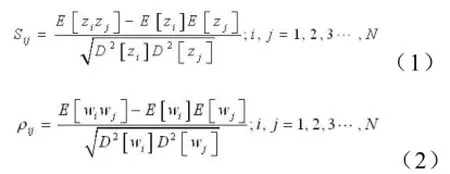
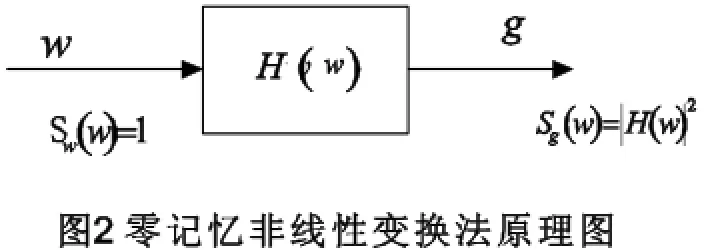
2常见海面噪声的建模与仿真
2.1相参Rayleigh分布杂波
由于Guass随机过程经过数次线性变换后得到的仍为Guass随机过程,因而Rayleigh分布的海面杂波的建模与仿真可通过下图所示的系统框图来实现。其中为复Guass随机过程,是一个线性滤波器。
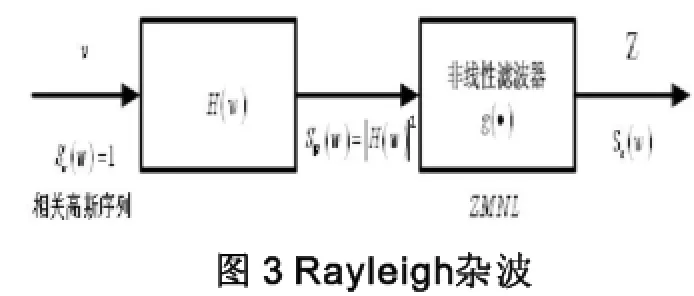
2.2相参Weibull分布
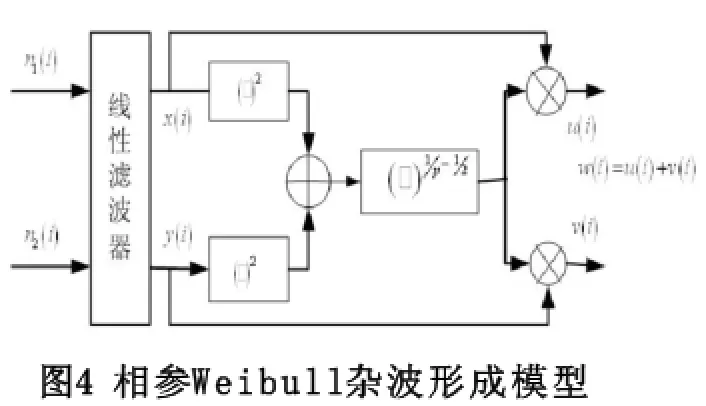
下图为相参Weibull分布的海面杂波仿真模型[12],图中:为两个正交的白Guass噪声序列;为理想条件下的正交Guass序列;为输出的复信号。
2.3采用ZMNL方法构造广义相参K分布序列
广义K分布杂波与上述两个杂波模型不同,其幅度统计特征可用两个独立随机变量的乘积来表述[12],
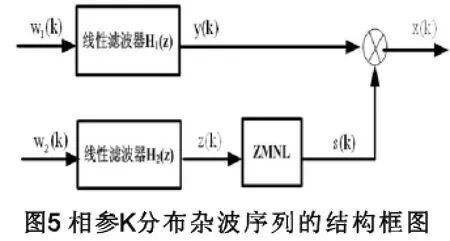
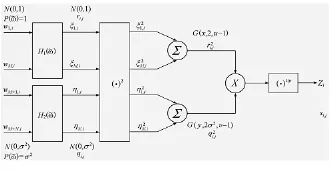
图6相参广义K分布序列流程图

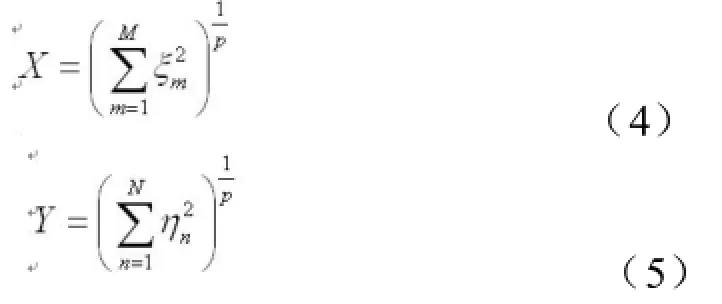
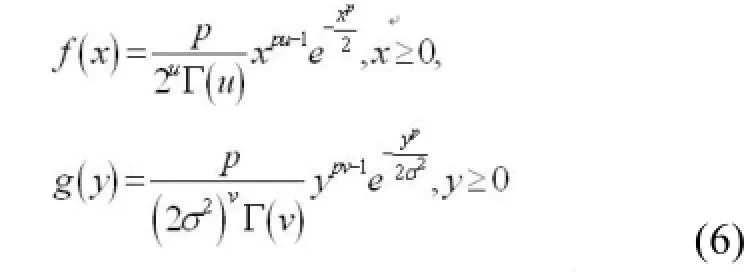
其中,M=2μN=2v,由Bayes公式知
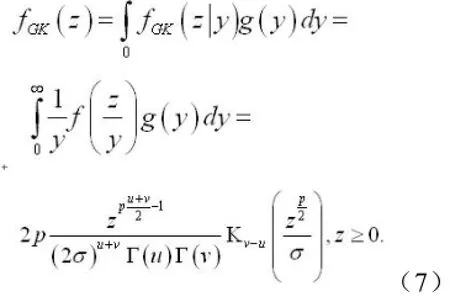
上式是广义K分布海面杂波模型的概率密度函数。其中,μ,v为形状参数,σ为尺度参数,为Gamma函数,为第二类修正的v阶 Bessel函数.当时,上式就是复合型K分布海杂波的密度函数。其步骤可分为两部分:
1)设计线性滤波器。根据已知相参广义K分布杂波的自相关函数确定其功率谱密度。再进行采样后并经过归一化处理,可得自相关函数序列通过插值法可得到对应的自相关系数和最后由自相关系数和归一化处理可得到线性滤波器和
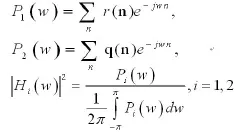
2)生成相参的广义随机K分布序列.其中基于ZMNL方法产生相参广义K分布序列流程如图3.3所示。
2.4基于SIRP法的相参K分布海面杂波的建模和仿真
下图给出了基于SIRP法构造相参K分布杂波序列的结构框图。图中,是一个复Guass白噪声,线性滤波器可由 ()x k的相关函数的来决定,为与互相独立的实Guass白噪声。根据图3.4所示的流程框图进行建模和仿真,来产生符合广义K分布的
3建模和仿真结果
1)杂波幅度分布
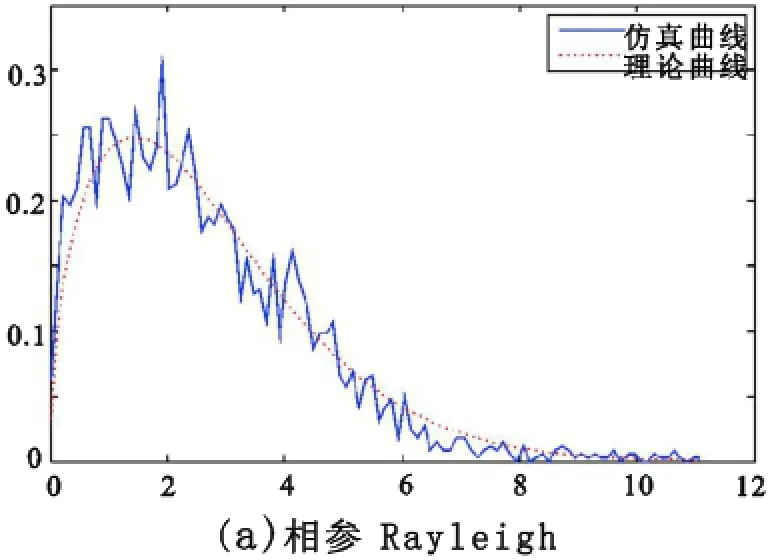
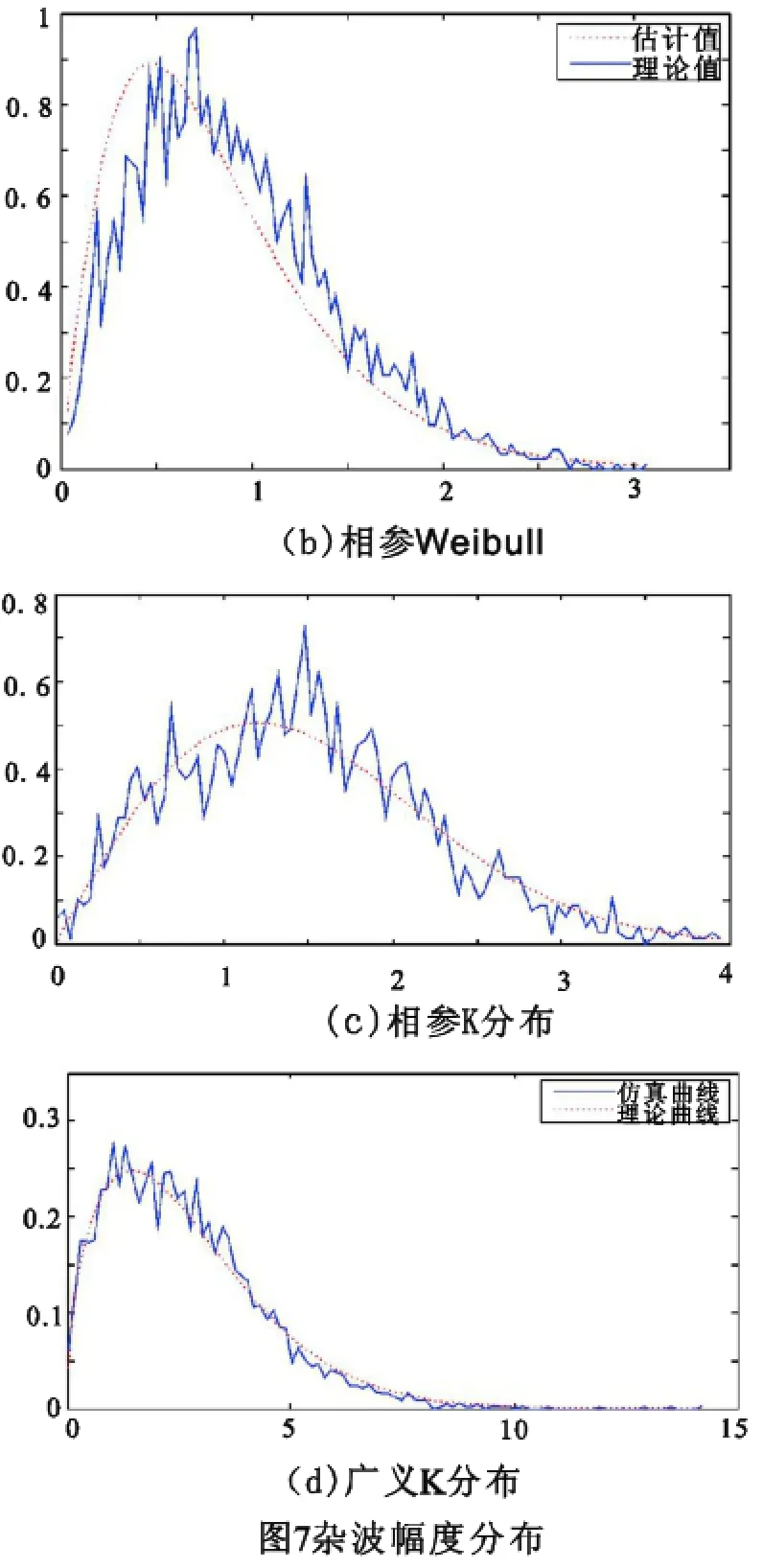
从上述四图可以看出:四种杂波的幅度分布都较好的与理论曲线拟合,且由于广义K发布的调制分量:
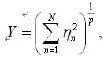
为N维,比相参K发布更加符合于K分布所以从上图可看出广义K分布拟合度更高,建模和仿真流程更加符合。
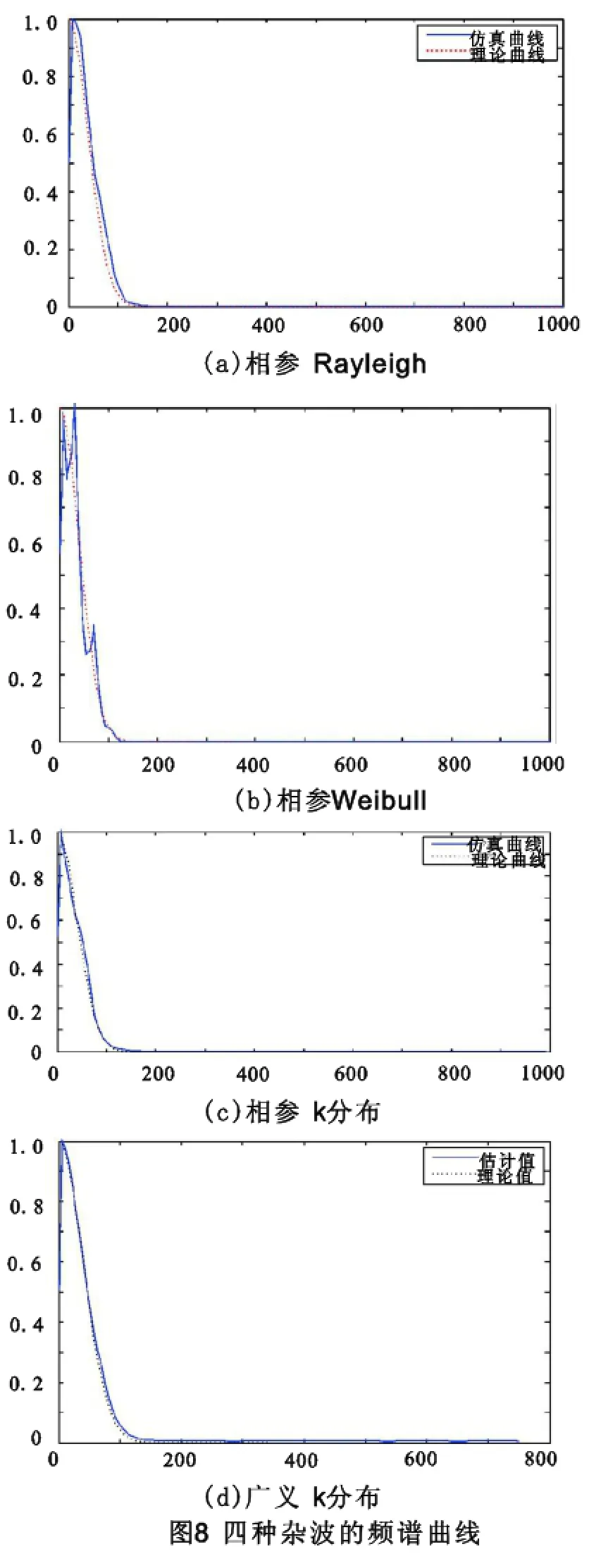
2)四种杂波的频谱曲线
从图8我们可以发现:杂波的频谱曲线与理论值保持一致。综上所述,本次课题设计的模型可信,建模和仿真方法正确。
4结束语
海面噪声的特征研究一直是我国为克服目前复杂电磁环境的重要项目,也是研究干扰对消必考虑的环境因素。而利用Matlab等数学软件结合各类参数来绘制海面噪声曲线是环境分析的重要方法。为了验证该模型的可行性,通过对该模型进行了编程建模和仿真,最终结果达到了预计的效果后,验证了模型的可信性。
[1]WardKD.Compoundrepresentationofhigh resolution sea clutter.Electronics Letters.1981,17(16):561-563.
[2]Jing Hu,Wen Wen Tung,Jian—Bo Gao.Modeling sea clutter as a nonstationary and nonextensive random process.IEEE International Radar Conference,2006:412-416.
[3]杨凤风,周智敏.基于ZMNL法的雷达杂波建模和仿真.现代雷达,2003,25(9):22-24.
[4]杨俊岭,吕韶呈,万建伟.一种新的相参k分布模型及其在海面噪声建模和仿真中的应用.系统建模和仿真报,2007,19(2):250-253.
[5]Matia,Ashkenazy Y.Multifractal properties of price fluctuations of stocks and commodities.2003,61(3):422-428.
[6]Kwapien,POswiecimka, andS.Drozdz. Components of ultifractality in high—frequency stock returns.Physics A,2005,35(10):466-474.
Simulation of Correlated Radar Clutter Based on ZMNL and SPIR
Gao Xin,Gou Chuanjie,Zhang Lei,He Fangmin
(Naval Univ.of Engineering,Wuhan 430033,China)
This paper researches sea clutter modeling from two aspects:zero memory nonlinearity,spherically invariant random process.First,coherent Rayleigh,coherent Weibull and Coherent K clutter are simulated with zero memory nonlinearity transform and spherically invariant random process,and the accuracy of these model compared with the theories is verified in the thesis.Considering the relativity of sea clutter and building up three model of power spectrum density and PDF are the features of this thesis.
sea clutter;coherent;ZMNL;SIRP
TP15
A
1003-4862(2016)07-0024-04
2015-12-08
高鑫(1992-),男,硕士。研究方向:电磁兼容。
