基于最优控制的一类忆阻混沌系统的同步

常文亭，李玉霞，黄　霞，张琳琳

(山东科技大学 电气与自动化工程学院,山东 青岛 266590)



基于最优控制的一类忆阻混沌系统的同步

常文亭，李玉霞，黄霞，张琳琳

(山东科技大学 电气与自动化工程学院,山东 青岛 266590)

摘要：本文基于线性二次型问题的最优控制理论，研究了蔡氏忆阻混沌系统的同步问题，提出了一种实现蔡氏忆阻混沌系统同步的方案。并利用李雅普诺夫稳定性定理证明了两个同构蔡氏忆阻混沌系统达到同步的充分条件。该方法能够实现控制能量消耗和同步误差的综合最优。数值仿真结果验证了文中所给方法的有效性。

关键词：混沌同步；忆阻混沌系统；最优控制；渐近稳定

自Pecora和Carroll[1]提出具有划时代意义的混沌同步以来，混沌同步在混沌保密通信、金融系统、生物医学等领域[2-6]得到了广泛的应用，许多新的混沌同步的方法相继产生，如自适应方法、神经网络方法、滑模控制方法等[7-10]。近年来，由于忆阻器具有非易失性、纳米尺寸及低功耗性[11-12]等优良特性，使得忆阻混沌系统的同步控制方法成为一个新的热点问题。文献[13]提出了一类四阶蔡氏忆阻混沌系统，并研究了其复杂的非线性行为。文献[14]通过采用脉冲控制的方法实现了四阶蔡氏忆阻混沌系统的同步，提高了忆阻混沌系统的工程应用潜力。然而，正如文献[15]指出：对于一个实际的物理系统，控制器的能量总是有限的。在实现混沌同步的过程中，就必须要考虑系统的控制能量最终要能够实现控制能量消耗及同步误差的综合最优[16]。因此，基于最优控制的混沌同步方法具有更高的应用价值。

本文对于蔡氏忆阻混沌系统的同步问题，考虑到控制能量的消耗，首先将性能指标确立为状态变量和控制变量的二次型函数，接着对该线性二次型问题求出其最优解，即得到系统所需的最优控制率，最后将最优控制率耦合到忆阻混沌系统实现了混沌同步，对于同一系统而且在相同初始条件下，与文献[14]脉冲同步相比，同步效果基本一致，但是本文同时实现了忆阻混沌系统的控制能量消耗和同步误差的综合最优。进一步的理论分析和数值仿真都证实了该方法的有效性。

图1　四维蔡氏忆阻混沌系统

1蔡氏忆阻混沌系统

文献[13]通过采用一个负电导-G与无源二端口光滑磁控忆阻器构成的有源忆阻电路代替蔡氏电路中的蔡氏二极管建立了一个四维自治蔡氏忆阻混沌系统(如图1)。

图1电路的动力学方程为：

(1)

式中，v1和 v2分别为电容 C1和 C2两端的电压，i3为流过电感 L 的电流，φ 是忆阻器的内部磁通，且w(φ)=m1+3m2φ2，m1、m2是大于零的实常数。

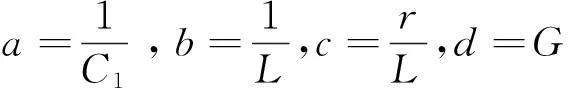
(2)

2蔡氏忆阻混沌系统的同步

2.1蔡氏忆阻混沌系统的最优控制率设计

假设驱动系统和响应系统，其状态变量分别用 (x1,x2,x3,x4),(y1,y2,y3,y4)来表示。驱动系统的状态方程用矩阵形式表示为：

(3)

参数 a，b，c，d，m1，m2均为大于零的实常数。类似地，响应系统为：

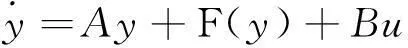
(4)

其中，控制向量u=-K(y-x)，K=R-1BTP，P>0。

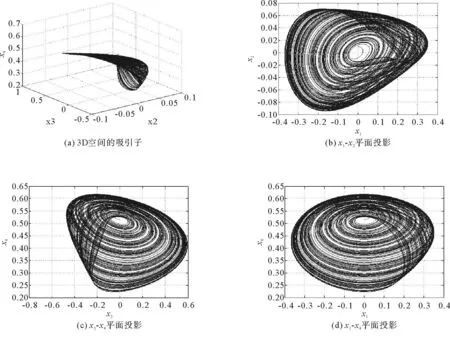
图2　系统(2)的混沌吸引子

定义同步误差向量e=y-x，由系统(9)和(10)，获得如下的同步误差系统：

(5)

因此，系统(3)和(4)的同步问题，转化为系统(5)的稳定性问题，只要保证系统(5)的平衡点是全局渐近稳定的，就可以实现系统(3)和(4)的同步。为衡量系统同步所消耗能量的大小，对系统 (5) 定义性能指标

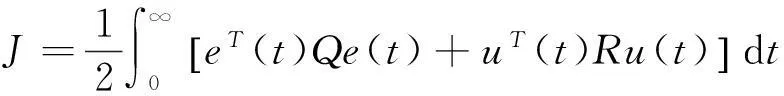
(6)

其中 Q∈R4×4，R∈R4×4是正定对称矩阵。下面给出主要结果。

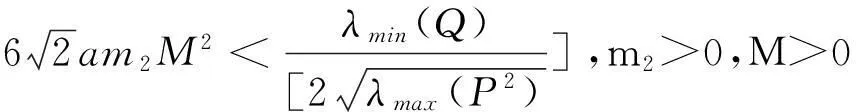
证明：对系统(5)，取Lyapunov函数

V(e)=eTPe，

(7)

其中P是对称正定矩阵。式(7)对时间t的导数为

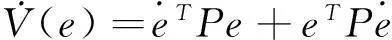
将式(5)及Riccati方程代入上式中有

-eT(Q+PBR-1BTP)e+2eTP[F(y)-F(x)]=

-eT(PBR-1BTP)e+eT(-Q)e+2eTP[F(y)-F(x)]

令V1=-eT(PBR-1BTP)e，V2=eT(-Q)e+2eTP[F(y)-F(x)]，

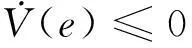
系统(2)为耗散系统，所以其状态轨迹是有界的，且由图2和图3可以明显得观察到。

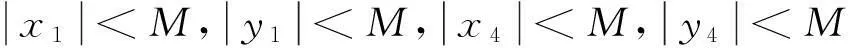
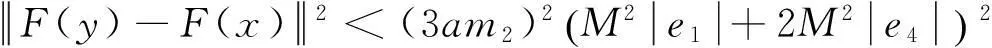
8M4(3am2)2‖e‖2

2eTP[F(y)-F(x)]≤2‖eTP‖·‖F(y)-F(x)‖=

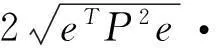
式中，λmax(P2)表示矩阵P的最大特征根。

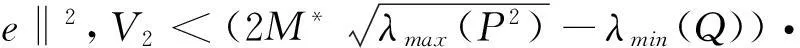
由李雅普诺夫稳定性定理知，系统(5)是全局渐近稳定的，即系统(3)和(4)是全局渐进稳定的，

定理得证。

基于前面的讨论，反馈增益矩阵K的算法总结如下：

(b) 选择合适的矩阵Q和矩阵R，结合矩阵A和B，求解Riccati方程得到矩阵P。如果P>0，则

把求得的矩阵P代入计算反馈增益矩阵K。

(c) 把矩阵K代入到系统(4)中，即可实现两个同步蔡氏忆阻混沌系统。

2.2仿真实验

显然 P>0。

进而算出增益矩阵

(8)

最优控制率为

(9)

性能指标最小值为

(10)

实现了忆阻混沌系统的控制能量消耗和同步误差的综合最优。

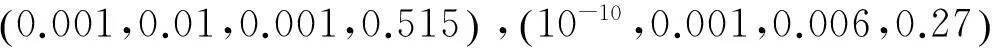
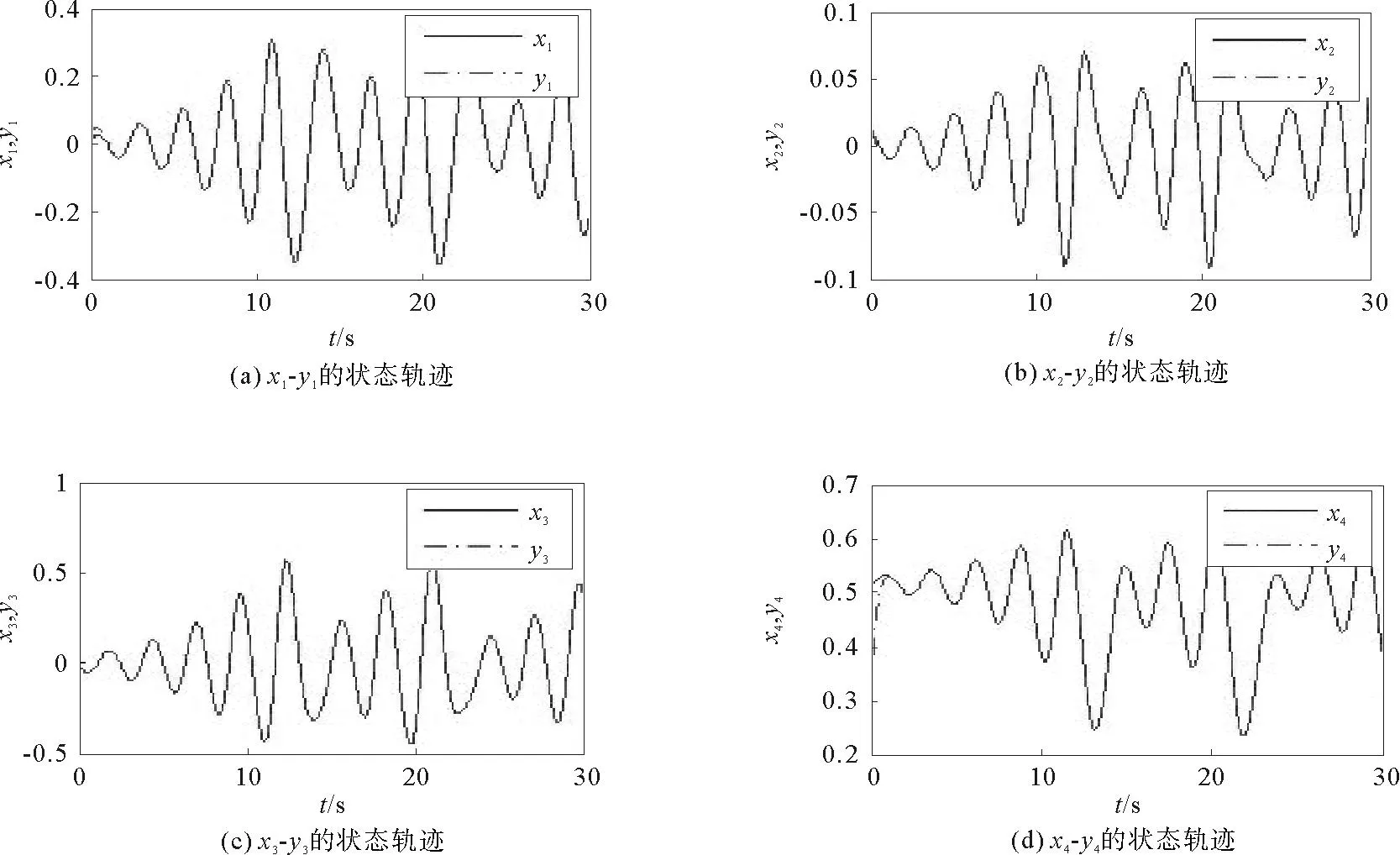
图3　蔡氏忆阻混沌电路驱动系统和响应系统的状态轨迹

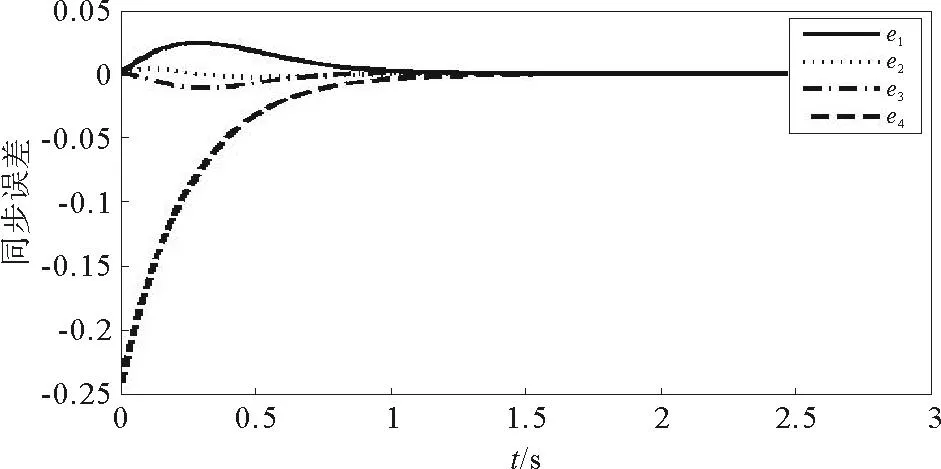
图4　两个同构蔡氏忆阻混沌系统的同步误差仿真结果

由图3和图4可以看出，当驱动系统和响应系统受到最优状态调节器的控制后，在系统运行最初的几秒内二者即实现了同步，并且同步效果明显。

3结论

本文针对文献[13]中提出的蔡氏忆阻混沌系统，利用线性二次型最优控制理论，研究了两个同构忆阻混沌系统的同步问题。根据李雅普诺夫稳定性定理，得到了使两个忆阻混沌系统同步的充分条件，并通过数值仿真验证了系统的同步行为，证明了该方法的可行性。而且，该方法实现了忆阻混沌系统的控制能量消耗和同步误差的综合最优。该系统中同步方法在增强通信系统保密性方面有很高的实用价值。

参考文献：

[1]PECORA L M,CARROLL T L.Synchronization in chaotic system[J].Physical Review Letters,1990,64(8):821-824.

[2]关新平.混沌控制及其在保密通信中的应用[M].北京：国防工业出版社，2002:226-271.

[3]黄登仕，李后强.非线性经济学的理论和方法[M].成都：四川大学出版社，1993:55-60.

[4]STROGATZ S H.Nonlinear dynamics and chaos:with applications to physics,biology,chemistry and engineering[M].Boston:Addison Wesley Publish,2001:15.

[5]MA J,CHEN Z,WANG Z,et al.A four-wing hyper-chaotic attractor generated from a 4-D memristive system with a line equilibrium[J].Nonlinear Dynamics,2015,81(3):1275-1288.

[6]PHAM V,VOLOS C,GAMBUZZA L.A memristive hyperchaotic system without equilibrium[J].The Scientific World Journal,2014,368986:9 .

[7]CHEN G,DONG X.On feedback control of chaotic continuous time system[J].IEEE Transaction on Circuits and Systems-I,1993,40(9):591-601.

[8]LI Y,LIU X,WANG G.Adaptive synchronization of hyperchaotic Lorenz systems based on parameter identification[J].Complex System and Applications：Modeling Control and Simulations,2007,14(S2):540-544.

[9]LIU X,LI Y.Synchronization of two different hyperchaotic systems using nonlinear control[J].Complex System and Applications—Modeling Control and Simulations,2007,14(S2):545-549.

[10]HUANG X,CAO J.Synchronization criteria for Lur’e systems by dynamic output feedback with time-delay[J].International Journal of bifurcation and chaos,2006,16(8):2293-2307.

[11]LI X,ZENG H,LI J.Hyperchaos in a 4-D memristive circuit with infinitely many stable equilibria[J].Nonlinear Dynamics,2015,79(4):2295-2308.

[12]包伯成.混沌电路导论[M].北京：科学出版社,2013:199.

[13]包伯成,刘中,许建平.忆阻混沌振荡器的动力学分析[J].物理学报，2010,59(6):3785-3793.

BAO Bocheng,LIU Zhong,XU Jianping.Dynamical analysis of memristor chaotic oscillator[J].Chinese Journal of Physics,2010,59(6):3785-3793.

[14]武花干,陈胜垚,包伯成.忆阻混沌系统的脉冲同步与初值影响研究[J].物理学报,2015,64(3):030501.

WU Huagan,CHEN Shengyao,BAO Bocheng.Impulsive synchronization and initial value effect for a memristor-based chaotic system[J].Chinese Journal of Physics,2015,64(3):030501.

[15]朱少平,钱富才,刘丁.不确定动态混沌系统的最优控制[J].物理学报,2010,59(4):225006.

ZHU Shaoping,QIAN Fucai,LIU Ding.Optimal control for uncertainty dynamic chaotic systems[J].Chinese Journal of Physics,2010,59(4):225006.

[16]郑大钟.线性系统理论[M].北京：清华大学出版社,2002:324.

(责任编辑：傅游)

收稿日期：2016-01-11

基金项目：国家自然科学基金项目(61473177,61473178)；教育部博士点基金项目(20133718110011).

作者简介：常文亭(1992—)，女，山东嘉祥人，硕士研究生，主要从事忆阻混沌电路的研究.E-mail：jnydcwt@163.com 李玉霞(1968—)，女，山东滨州人，教授，博士生导师，主要从事控制理论及机器人技术等方面的研究，本文通信作者.E-mail：yuxiali2004@126.com

中图分类号：N941.7

文献标志码：A

文章编号：1672-3767(2016)04-0093-06

Synchronization of Chua’s-Circuit-Based Memristive Chaotic Systems Based on Optimal Control

CHANG Wenting,LI Yuxia,HUANG Xia,ZHANG Linlin

(College of Electrical Engineering and Automation,Shandong University of Science and Technology,Qingdao,Shandong 266590,China)

Abstract:This paper studies the synchronization of two identical Chua’s-circuit-based memristive chaotic systems based on linear quadratic optimal control.A scheme is proposed to synchronize the two chaotic systems.The Lyapunov stability theorem was adopted to prove the sufficient conditions for the synchronization of the two systems.With this method,the optimization on both energy consumption and synchronization error could be realized synthetically.Finally,the simulation results testified the effectiveness of the proposed method.

Key words:Chaos synchronization;memristive chaotic systems;optimal control;asymptotically stable