寄生参数对SiC MOSFET栅源极电压影响的研究

巴腾飞　李　艳　梁　美（北京交通大学电气工程学院　北京　100044）



寄生参数对SiC MOSFET栅源极电压影响的研究

巴腾飞李艳梁美
（北京交通大学电气工程学院北京100044）

为分析寄生参数对开关过程中碳化硅（SiC）MOSFET栅源极电压的影响，首先建立了基于同步Buck变换器的SiC MOSFET开通和关断过程的数学模型；然后通过仿真和实验结果对比，验证了寄生参数带来的影响；最后分析了开关过程中各寄生参数对SiC MOSFET栅源极电压的影响。

SiC MOSFET寄生参数开关模型栅源极电压

0　引言

新型宽禁带半导体器件碳化硅（Silicon Carbide，SiC）MOSFET以其高速开关能力、低通态电阻、高结温、高耐压等特点［1-4］得到广泛应用。其优良的开关性能有利于减小开关损耗及死区时间，提高开关频率，减小变换器中无源元件的体积，有效提高变换器的功率密度［5-8］。而随着开关频率的提高，开关速度也进一步提升，开关过程中产生更高的 dv/dt［9］。同时SiC MOSFET的阈值电压较低［7］，栅源极能承受的最大负向电压较小，且栅极内阻较大，在桥式电路中应用SiC MOSFET受其他开关管开关动作的影响会更容易出现误导通或栅源极击穿，制约了SiC MOSFET的应用。

在高频电路中寄生参数对开关管开关特性的影响越发明显。文献［10，11］分析了寄生电容和栅极阻抗对MOSFET栅源极电压的影响，并进行了仿真对比，但未进行实验验证。文献［12］研究了共源电感对MOSFET栅源极电压的影响，但并未考虑开关回路中其他寄生电感的影响。二极管的反向恢复特性对开关管的开关过程也具有重要影响［13，14］。文献［15］不仅考虑了开关回路的寄生电容和寄生电感，还考虑了MOSFET的寄生二极管反向恢复特性的影响。但主要分析了寄生参数对MOSFET误导通的影响，而没有研究寄生参数对MOSFET栅源极击穿的影响。本文将对上述两种现象进行具体的分析研究，讨论各寄生参数对MOSFET栅源极电压的影响。

为了研究各寄生参数对MOSFET栅源极电压的影响，还需要建立仿真模型进行仿真分析。文献［16］给出了SiC MOSFET的物理模型，但此模型不能用于分析SiC MOSFET的开关过程。文献［17］中的数学模型计算复杂，为简化计算忽略了部分寄生参数的影响，不能准确反映某些寄生参数的影响。文献［15］中基于同步Buck变换器的数学模型不仅包含了开关回路中所有的寄生参数，而且求解简单，但仅分析了MOSFET的开通过程，并未分析MOSFET的关断过程。由于同步Buck变换器中两只MOSFET的结构类似于桥式结构，在主开关管开关过程中也会造成同步开关管的栅源极电压变化，且变换器结构简单，利于分析研究，因此本文建立了基于同步Buck变换器的SiC MOSFET开通和关断过程的数学模型。利用此数学模型不仅能分析SiC MOSFET的开通和关断过程以及其栅源极电压发生变化的具体原因，还能对寄生参数的影响进行仿真验证。

为了研究寄生参数对SiC MOSFET栅源极电压的影响，本文首先建立了基于同步Buck变换器的主开关管开通和关断过程的数学模型，分阶段分析SiC MOSFET的开通和关断过程及其栅源极电压发生变化的具体原因；然后通过实验和仿真对比来验证寄生参数的影响；最后分析了开关回路中各寄生参数对SiC MOSFET栅源极电压的影响。

1　开关过程的数学模型

考虑寄生参数的同步Buck变换器电路如图1所示。图中虚线框中表示带封装的开关管Q1和Q2。Q1的寄生参数包括极间寄生电容 Cgs1、Cgd1、Cds1，寄生电感 Lg1_in、Ld1_in、Ls1_in以及栅极内部电阻Rg1_in。Q2的寄生参数包括极间寄生电容 Cgs2、Cgd2、Cds2，寄生电感 Lg2_in、Ld2_in、Ls2_in以及栅极内部电阻Rg2_in。外电路中的寄生参数包括 PCB引线中的寄生电感 Lg1_ex、Ld1_ex、Ls1_ex、Lg2_ex、Ld2_ex、Ls2_ex。除此之外，驱动电路中的驱动电阻包括 Q1的开通电阻Rg1_on和关断电阻Rg1_off以及Q2的开通电阻 Rg2_on和关断电阻 Rg2_off。为简化计算，令 Lg1= Lg1_in+Lg1_ex，Ld1=Ld1_in+Ld1_ex，Ls1=Ls1_in+Ls1_ex；Lg2=Lg2_in+Lg2_ex，Ld2=Ld2_in+Ld2_ex，Ls2=Ls2_in+ Ls2_ex。从图1中可知，id1为 Q1的漏极电流，ig1为 Q1的栅极电流，ich1为Q1的沟道电流；vgs1为g1端和s1端之间的电压，vgd1为g1端和d1端之间的电压，vds1为d1端和s1端之间的电压，vGS1为G1端和 S1端之间的电压；id2为Q2的漏极电流，ig2为Q2的栅极电流，if为流过 VDb2的电流；vgs2为 g2端和 s2端之间的电压，vgd2为 g2端和 d2端之间的电压，vds2为 d2端和 s2端之间的电压，vGS2为 G2端和 S2端之间的电压；Vpulse1和 Vpulse2为驱动电源，VDC为输入电压，IL为负载电流。

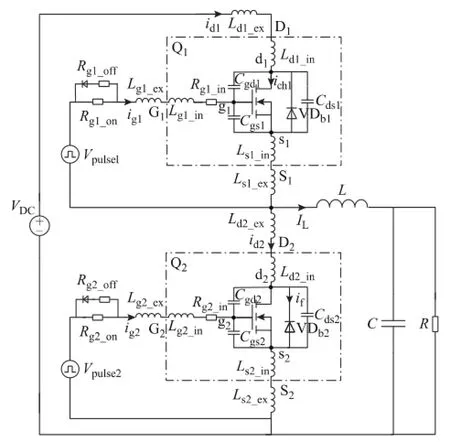
图1　考虑寄生参数的同步Buck变换器Fig.1　Synchronous Buck converter considering parasitic elements

利用图1给出的电路建立SiC MOSFET开关过程的数学模型，用于仿真分析开关过程中寄生参数对SiC MOSFET栅源极电压的影响。在建立开关过程数学模型的过程中利用微分状态方程求解各变量的数学表达式，微分状态方程的通用表达式为

式（1）可近似简化为

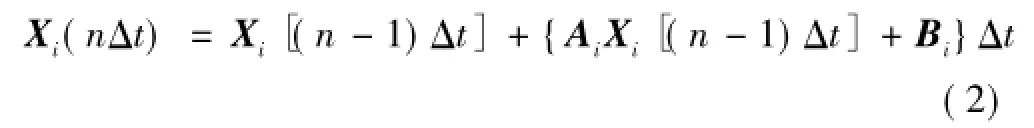
式中，n=1，2，3，…；Δt为求解步长；i=1～4分别表示Q1开通过程的第1～第4阶段，i=5～9分别表示Q1关断过程的第1～第5阶段。各阶段的Xi的表达式不同，但都可以利用此方法进行求解，且Ai和Bi的表达式如附录所示。

1.1Q1开通过程的数学模型

Q1的开通过程可划分为4个阶段，相关变量的波形如图2所示。Q1的开通过程如下:

1）第1阶段（t0～t1）

在t0时刻，Q1的驱动信号变为高电平，vgs1由关断电压VG2开始上升，直至vgs1上升至阈值电压 Vth1。在此过程中，Q2的寄生二极管VDb2续流，Q1仍处于截止状态，漏源极电压vds1保持不变，漏极电流id1=0。可建立式（3）～式（5），并列写状态方程，i=1。其中，X1=［ig1vgs1］T。

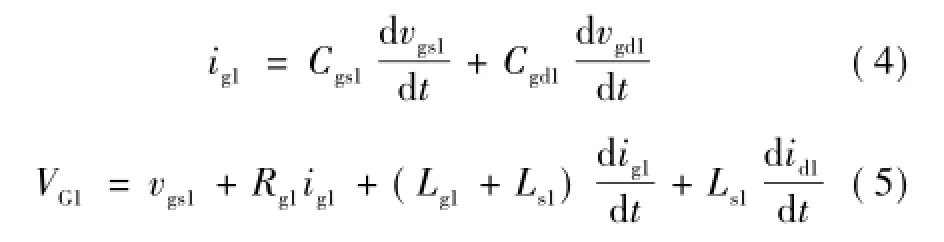
式中，VG1为Q1的驱动开通电压；Vth1为Q1的阈值电压，V；Rg1=Rg1_on+Rg1_in，Ω。

2）第二阶段（t1～t2）

在t1时刻，vgs1上升到Vth1，Q1开始导通，其漏极电流 id1从零开始线性增大，同时 id2负向减小。由于寄生电感 Ld1、Ls1、Ld2及 Ls2上有压降，Q1的漏源极电压 vds1降低。id1增大至负载电流 IL时，寄生二极管 VDb2进入反向恢复阶段，id1继续线性上升，当流过VDb2的电流达到负向恢复电流峰值IRR时此阶段结束。可建立式（6）～式（12），式（3）～式（5）仍然成立，列写状态方程，i=2。其中，

式中，gfs1为 Q1的跨导系数，S；Rg2=Rg2_off+Rg2_in，Ω；VG2为Q2的驱动关断电压，V。

3）第三阶段（t2～t3）

在t2时刻，寄生二极管VDb2的反向恢复电流if达到峰值电流IRR。此后，if逐渐减小，vds1迅速下降，且vds2迅速上升，其变化率为 dvds2/dt。此过程中 Cgd2充电，Cgd2上的电流近似为Cgd2dvds2/dt，此电流流经Q2的栅极并流过Q2的寄生电感Cgs2，造成Q2的栅极电位升高，其栅源极电压vgs2正向增大。随着vds2的上升，Cgs2持续充电，栅源极电压vgs2继续增大。直至vds2上升至母线电压VDC时此阶段结束。建立式（13）和式（14），式（3）～式（12）仍然成立，列写状态方程，i=3。其中，X3=［id1ig1vgs1vds1ig2vgs2vds2］T。

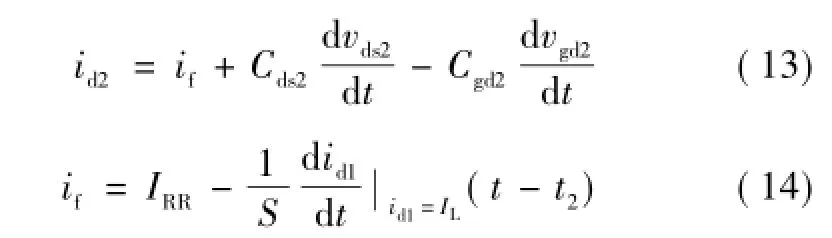
式中，IRR为Q2的寄生二极管VDb2的反向恢复峰值电流，A；S为Q2的寄生二极管VDb2的软因子。

4）第四阶段（t3～t4）

在t3时刻，vds1下降至通态电压，vgs1继续上升至VG1。在此过程中，由于寄生电容和寄生电感的影响，vds2发生过冲及振荡。当vds2达到峰值时，Q2的栅源极电压vgs2达到峰值。建立式（15），式（3）～式（14）仍然成立，i=4。其中，X4=［id1ig1vgs1ig2vgs2vds2］T。

vds1=Rds1id1（15）

式中，Rds1为Q1的沟道通态电阻，Ω。

在t5时刻，当vgs1到达开通电压VG1时，Q1完全导通，其开通过程结束。

图2　Q1开关过程中的主要波形Fig.2　Key waveforms during switching transient of Q1

1.2Q1关断过程的数学模型

Q1的关断过程划分为5个阶段，关断过程中相关变量的波形如图2所示。Q1的关断过程如下:

1）第一阶段（t5～t6）

在t5时刻，当开关管Q1的驱动信号变成低电平时，Q1的栅源极电压vgs1开始下降，vgs1下降至密勒电压Vmiller前，Q1仍处于饱和导通状态。建立式（16），式（3）和式（4）仍然成立，并列写状态方程，i=5。其中，X5=［ig1vgs1］T。

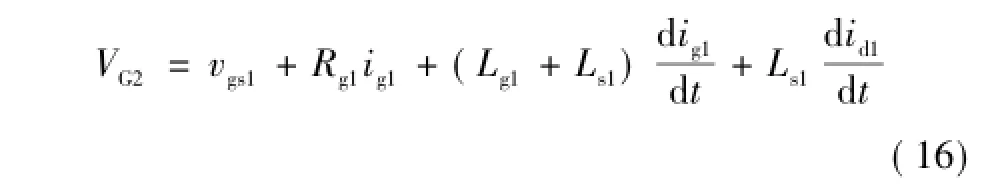
式中，VG2为 Q1的驱动关断电压，V；Rg1=Rg1_in+ Rg1_off//Rg1_on，Ω。

2）第二阶段（t6～t7）

在t6时刻，当vgs1降至Vmiller时，漏源极电压vds1由通态电压开始上升，在此过程中vgs1维持在Vmiller不变。此阶段式（3）、式（4）、式（16）仍然成立，列写状态方程，i=6。其中，X6=［ig1vds1］T。

3）第三阶段（t7～t8）

在t7时刻，Q1进入放大区后，漏源极电压vds1开始迅速上升，寄生电容Cgd1和Cds1充电；而Q2的漏源极电压vds2开始下降，其变化率为dvds2/dt。寄生电容Cgd2和Cds2放电，Cgd2上的电流近似为 Cgd2dvds2/dt，此电流流经Q2的栅极并流过寄生电感Cgs2，造成Q2的栅极电位下降，其栅源极电压 vgs2负向增大。随着vds2的下降，Cgs2持续充电，栅源极电压继续负向增大。当vds2下降至-Vf时寄生二极管VDb2导通，Q2的栅源极电压vgs2达到峰值，此过程结束。在此过程中Q2的漏极电流 id2负向增加，同时 id1减小。建立式（17），式（3）、式（4）、式（6）～式（12）和式（16）仍然成立，列写状态方程，i=7。其中，X7= ［id1ig1vgs1vds1ig2vgs2vds2］T。

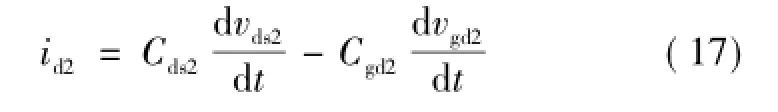
4）第四阶段（t8～t9）

在t8时刻，当开关管 Q2的漏源极电压 vds2下降至-Vf后保持不变，Q2的寄生二极管VDb2开始导通，开关管Q1和Q2开始换流，此过程中Q2的栅源极电压vgs2负向减小。在此过程中vds1发生过冲及振荡。式（3）、式（4）、式（6）～式（12）、式（16）和式（17）仍然成立，列写状态方程，i=8。其中，X8=［id1ig1vgs1vds1ig2vgs2vds2］T。

5）第五阶段（t9～t10）

在t9时刻，开关管Q1关断，由于寄生电感和寄生电容的作用vds1振荡。开关管Q2的寄生二极管VDb2续流。在此过程中，vgs1继续下降。建立式（18），式（3）、式（4）、式（8）～式（12）、式（16）和式（17）仍然成立，列写状态方程，i=9。其中，X9= ［id1ig1vgs1vds1ig2vgs2］T。

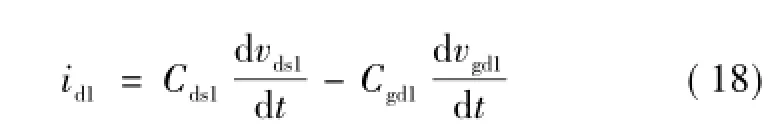
在t10时刻，当vgs1下降至关断电压VG2时，Q1的关断过程结束。

建立的数学模型还能准确描述G2端和S2端之间的电压，由图1可知，vGS2和vgs2关系为

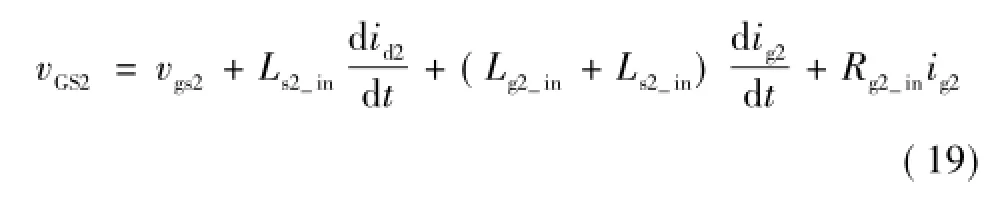
2　仿真和实验验证

为验证寄生参数对SiC MOSFET栅源极电压的影响以及建立的数学模型的准确性，本文对比了寄生参数变化时仿真和实验结果中vGS2的变化。仿真和实验中的相关参数见表1。开关管选用的是CREE公司生产的1200 V/31.6 A SiC MOSFET（C2M0080120D）。

表1　变换器的相关参数Tab.1　The parameters of converter

图3和图4分别为Q1开通过程中vGS2的仿真波形和实验波形。从图3a～图3g和图4a～图4g中可看出，随着 Rg1、Lg1、Ls1、Cgs1、Cgd1和 Cds1的增大，vGS2的峰值减小。Ld1增大时 vGS2的峰值增大。从图4h～图4n可看出，Rg2、Lg2、Cgd2、Ld2和Ls2增大时vGS2的峰值增加，Cgs2和Cds2增大时vGS2的峰值减小。

图3和图4中的电压波形会出现负向过冲。究其原因，是因为在id2上升过程中，Q2的二极管仍处于导通状态，而共源电感 Ls2上的电压为 Ls2did2/dt，会使vGS2的波形上出现正向电压尖峰。当vds2上升过程中由于位移电流Cgd2dvds2/dt的作用，使得Lg2_in和Ls2_in上的电压发生变化，造成波形出现负向电压尖峰。

图5和图6分别为Q1关断过程中vGS2的仿真波形和实验波形。从图6a～图6g中可看出，随着Rg1、Lg1、Ld1、Ls1、Cgs1、Cgd1和 Cds1的增大，vGS2的峰值减小。从图6h～图6n中可看出，Rg2、Lg2、Cgd2和Ls2增大时vGS2的峰值增加，Cgs2、Ld2、Ls2和 Cds2增大时 vGS2的峰值减小。

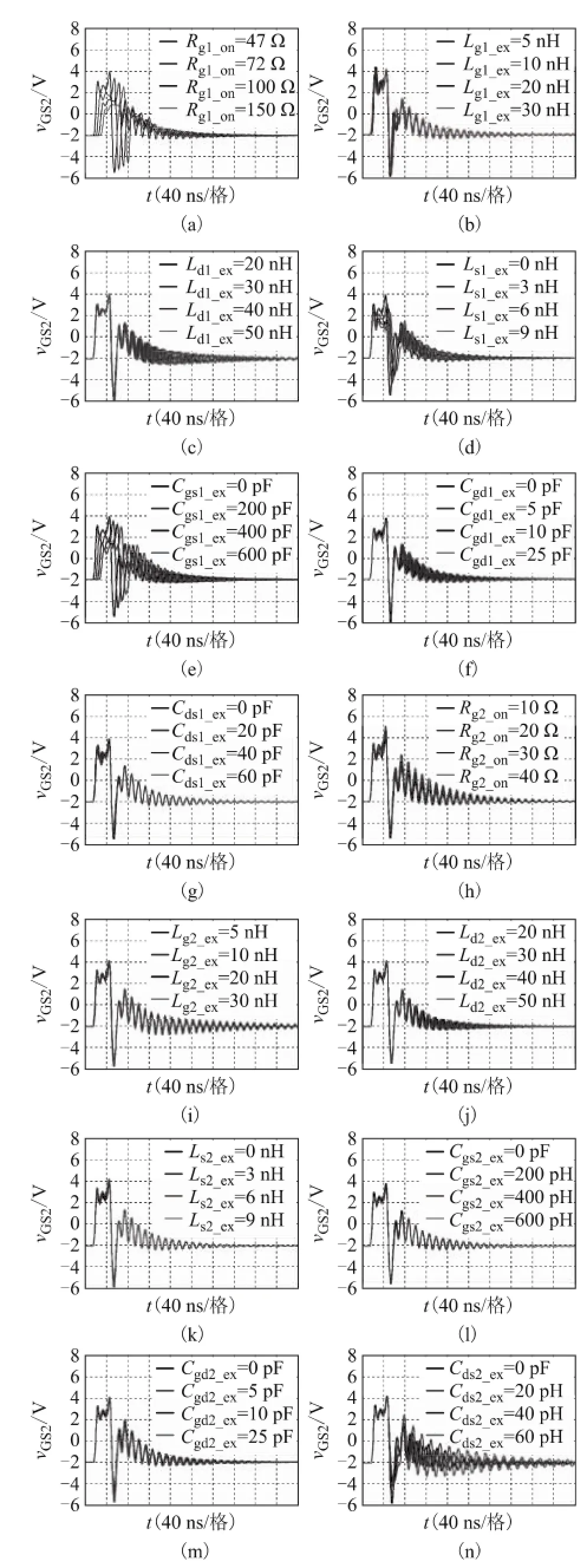
图3　Q1开通过程中vGS2的仿真波形Fig.3　Simulated switching waveforms of vGS2during turn-on transient of Q1

图4　Q1开通过程中vGS2的实验波形Fig.4　Experimental switching waveforms of vGS2during turn-on transient of Q1

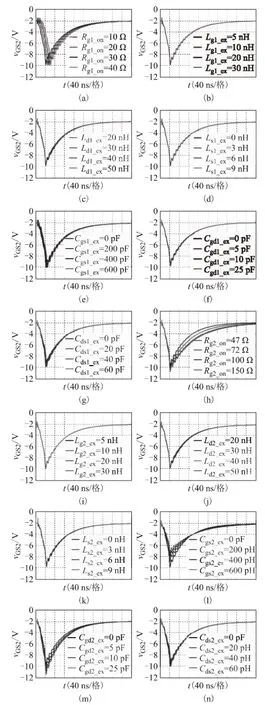
图5　Q1关断过程中vGS2的仿真波形Fig.5　Simulated switching waveforms of vGS2during turn-off transient of Q1

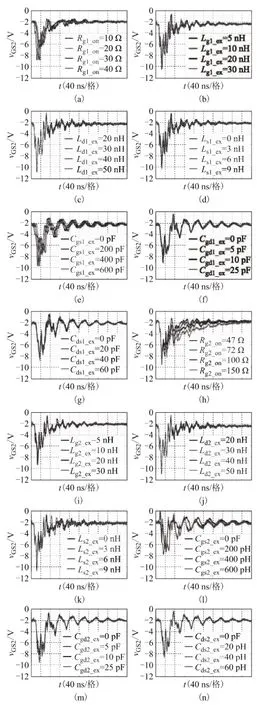
图6　Q1关断过程中vGS2的实验波形Fig.6　Experimental switching waveforms of vGS2during turn-off transient of Q1

通过Matlab仿真结果和实验对比，可看出建立的开关模型能够准确地反映寄生参数对vGS2的影响。但由于在建立SiC MOSFET开关过程的数学模型过程中，提取的寄生参数的值和实际值之间有误差，且没有考虑寄生电感之间的耦合等因素，造成波形不能完全和实验波形相吻合。实验波形中出现高频振荡，是因为当vds2上升到最大值或减小到最小值后，由于开关回路中寄生电感和寄生电容的谐振，造成vds2电压波形出现振荡，此时流经结电容Cgd2的电流为Cgd2dvds2/dt，其大小和方向会随vds2的振荡而发生变化。此电流分为两部分，一部分电流流经Rg2和Lg2，另一部分电流流经Cgs2和Ls2。当vds2波形出现振荡时，流经结电容Cgd2的电流 Cgd2dvds2/dt的方向发生变化，造成驱动回路中寄生电感Lg2、Ls2和寄生电感 Cgs2产生谐振，使vGS2的波形出现高频振荡。

其次，寄生参数的大小会影响到开关管的开关速度，并且影响开关管的电压电流尖峰大小及其振荡情况。这些也都影响到开关过程中vGS2的波形。在建立数学模型时需要提取寄生电感和寄生电容的值。由于设备精度的原因，提取的数值和实际值之间会存在误差。而寄生电容则是利用数据手册上的曲线进行拟合，但是没有考虑温度等因素对寄生电容的值的影响。这会造成仿真波形和实验波形之间不能完全吻合。

另外，开关管的引脚上存在寄生电感。如图1所示，引脚G2和S2的寄生电感分别是Lg2_in和Ls2_in。流过寄生电感Lg2_in和Ls2_in的电流方向决定了这两个寄生电感之间的耦合关系。寄生电感之间的耦合会影响到G2和S2之间的电压vGS2。在建立的数学模型中，并没有考虑寄生电感之间的耦合关系。因此在一定程度上会造成实验波形和仿真波形之间存在误差。

但SiC MOSFET栅源极电压尖峰的产生原因是SiC MOSFET漏源极电压突变引起的栅源极电压变化，建立的数学模型能反映出这一现象产生的原因以及寄生参数对SiC MOSFET栅源极电压的影响。

3　寄生参数对vgs2影响的分析

Q2的误导通或栅源极击穿是由vgs2决定的。因此，可利用已建立的模型分析寄生参数对vgs2的影响，并进行仿真验证。

图7为Q1开关过程中Q2的驱动等效电路。从图中可看出，VG2为驱动关断电压，Cgd2dvds2/dt为流过Q2栅极的电流，Ls2did2/dt为共源电感Ls2上的压降，其电流、电压的参考方向如图7所示。Q2处于关断状态时，其栅源极电压vgs2的值为VG2。但在Q1开关过程中，由于电压源Ls2did2/dt和电流源Cgd2dvds2/dt的共同作用，导致vgs2发生变化。

图7　Q2驱动等效电路Fig.7　Equivalent driver circuit of Q2

利用图7的电路分析寄生参数对vgs2的影响。电流源Cgd2vds2/dt中的电流经过Q2的栅极，分别流过Rg2、Lg2以及Cgs2。其中，寄生参数Rg1、Lg1、Ls1、Cgs1、Cgd1或Cds1减小时，Q1的开关速度变快，Q2的漏源极电压变化率dvds2/dt增大，同时 Cgd2dvds2/dt也增大；同步开关管Q2的寄生电容Cds2减小时，Q2的漏源极电压变化率dvds2/dt增大；同步开关管Q2的寄生电容Cgd2增大时，Cgd2dvds2/dt也增大。这 3种情况都使得Cgd2dvds2/dt增大，流过Cgs2的电流也增大，因此Q2的栅源极电压尖峰增大。

寄生参数Rg2、Lg2越大，则Q2的栅极阻抗越大，电流源Cgd2vds2/dt中越多的电流分量流过Cgs2，则 Q2的栅源极电压尖峰越大。Cgs2增大时，其所在支路的阻抗减小，电流源Cgd2vds2/dt中流过Cgs2的电流分量增大，但同时流过Rg1和Lg1的电流减小，因此vgs2的绝对值减小，即Q2的栅源极正向和负向电压尖峰都减小。Ls2did2/dt随Ls2增大而增大。如图7a所示，在Q1开通过程中 Ls2did2/dt的增大使电流源 Cgd2vds2/dt中流过Cgs2的电流分量增多，因此Q2的栅源极正向电压尖峰增大。如图7b所示，Q1关断过程中Ls2did2/dt增大时流过Cgs2的电流分量减小，因此Q2的栅源极负向电压尖峰减小。

Ls2did2/dt随Ls2增大而增大。如图7a所示，在Q1开通过程中Ls2did2/dt的增大使得电流源Cgd2vds2/dt中流过Cgs2的电流分量增多，因此Q2的栅源极正向电压尖峰增大。如图7b所示，在Q1关断过程中Ls2did2/dt增大时流过Cgs2的电流分量减小，因此Q2的栅源极负向电压尖峰减小。

如图7a所示，在Q1开通过程中，图1中的寄生电感Ld1和Ld2的增大使得Q2的漏源极电压尖峰增大，电流源Cgd2vds2/dt的作用时间增长，因此有更多的电流流过Cgs2，也导致Q2的栅源极正向电压尖峰增大。如图7b所示，在Q1关断过程中Ld1和Ld2的增大使得Q2的漏源极电流变化率did2/dt减小，共源电感Ls2上的压降Ls2did2/dt也减小。这使得电流源Cgd2vds2/dt中流过Rg2和Lg2的电流分量增多，而流过Cgs2的电流分量减小，Q2的栅源极负向电压尖峰也随之减小。

4　结论

本文建立了适用于分析寄生参数对栅源极电压影响的SiC MOSFET开关过程的数学模型，在此基础上研究了各寄生电感、电容和电阻对SiC MOSFET栅源极电压的影响。通过比较仿真和实验结果，得出以下结论:

寄生参数对SiC MSOFET栅源极电压的影响方式有3种:①Rg1、Lg1、Ls1、Ld1、Cgs1、Cgd1、Ld2、Cds1和Cds2影响Q2的漏源极电压变化率dvds2/dt，并和寄生电容Cgd2共同决定Cgd2dvds2/dt的大小，Cgd2dvds2/dt越大，Q2的栅源极电压尖峰越大；②Rg2和Lg2越大，或Cgs2越小，流过寄生电容Cgs2的电流越多，则Q2的栅源极电压尖峰越大；③Ls2越大，则开关过程中其两端压降越大，造成SiC MOSFET的栅源极正向电压尖峰越大，而栅源极负向电压尖峰越小。本文的研究成果为变换器布局设计以及器件的参数选择提供了一定的理论基础。

附录

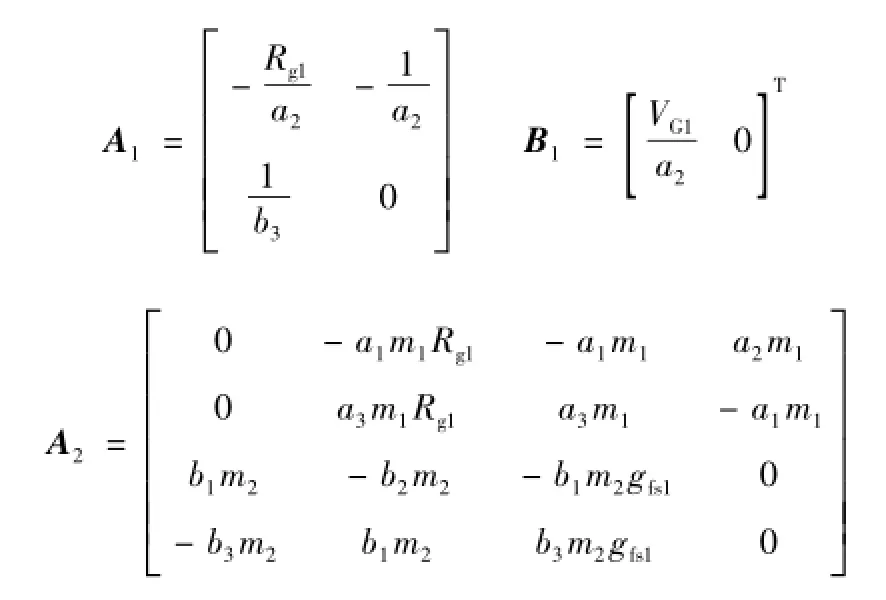
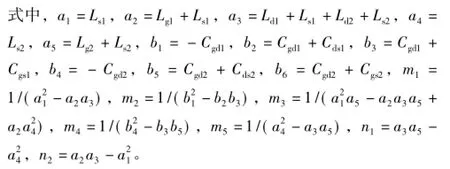
［1］祁锋，徐隆亚，王江波，等.一种为碳化硅MOSFET设计的高温驱动电路［J］.电工技术学报，2015，30（23）:24-31.

Qi Feng，Xu Longya，Wang Jiangbo，et al.A high temperature gate drive circuit for SiC MOSFET［J］. Transactions of China Electrotechnical Society，2015，30（23）:24-31.

［2］梁美，郑琼林，可翀，等.SiC MOSFET、Si CoolMOS 和IGBT的特性对比及其在DAB变换器中的应用［J］.电工技术学报，2015，30（12）:41-50.

LiangMei，ZhengQionglin，KeChong，etal. Performance comparison of SiC MOSFET，Si CoolMOSand IGBT for DAB converter［J］.Transactions of China Electrotechnical Society，2015，30（12）:41-50.

［3］陈思哲，盛况.4 700 V碳化硅PiN整流二极管［J］.电工技术学报，2015，30（22）:57-61.

Chen Sizhe，Sheng Kuang.4 700 V SiC PiN rectifier ［J］.Transactions of China Electrotechnical Society，2015，30（22）:57-61.

［4］任小永，David Reusch，季澍，等.氮化镓功率晶体管三电平驱动技术［J］.电工技术学报，2013，28 （5）:202-207.

Ren Xiaoyong，David Reusch，Ji Shu，et al.Threelevel drivingmethodforGaNpowertransistor［J］. Transactions of China Electrotechnical Society，2013，28（5）:202-207.

［5］Fujita H.A resonant gate-drive circuit with opticallyisolated control signal and power supply for fast-switching and high-voltage power semiconductor devices［J］.IEEE Transactions on Power Electronics，2013，28（11）: 5423-5430.

［6］Zhang Zheyu，Wang F，Tolbert L M，et al.A gate assist circuit for cross talk suppression of SiC devices in a phase-leg configuration［C］//IEEE Energy Conversion CongressandExposition， Denver， CO， 2013: 2536-2543.

［7］Zhang Zheyu，Wang F，Tolbert L M，et al.Active gate driver for crosstalk suppression of SiC devices in a phaselegconfiguration［J］.IEEETransactionsonPower Electronics，2014，29（4）:1986-1997.

［8］何骏伟，陈思哲，任娜，等.4 500 V碳化硅SBD和JFET功率模块的制备与测试［J］.电工技术学报，2015，30（17）:63-69.

He Junwei，Chen Sizhe，Ren Na，et al.Fabrication and testing of 4 500 V SiC SBD and JFET power modules ［J］.Transactions of China Electrotechnical Society，2015，30（17）:63-69.

［9］张云，徐衍亮，李豹.基于动态电源的MOSFET驱动优化［J］.电工技术学报，2013，28（12）: 269-275.

ZhangYun，XuYanliang，LiBao.Researchon optimization of MOSFET driving based on dynamic power source［J］.TransactionsofChinaElectrotechnical Society，2013，28（12）:269-275.

［10］Zhao Qun，Stojcic G.Characterization of Cdv/dt induced power loss in synchronous buck DC-DC converters［J］. IEEE Transactions on Power Electronics，2007，22（4）: 1503-1508.

［11］Xu Shen，Sun Weifeng，Sun Daying.Analysis and design optimization of brushless DC motor's driving circuit considering the Cdv/dt induced effect［C］//IEEE Energy Conversion Congress and Exposition，Atlanta，GA，2010:2091-2095.

［12］Yang B，Zhang J.Effect and utilization of common sourceinductanceinsynchronousrectification［C］// TwentiethAnnualIEEEAppliedPowerElectronics Conference and Exposition，2005，3:1407-1411.

［13］ 孟庆云，马伟明，孙驰，等.考虑二极管非理想特性的中点钳位三电平电路的分析［J］.电工技术学报，2010，25（6）:40-46.

Meng Qingyun，Ma Weiming，Sun Chi，et al.The NPC three-level circuit considering nonideal characteristic of diode［J］.TransactionsofChinaElectrotechnical Society，2010，25（6）:40-46.

［14］ 李方正，徐勤富，赖建军，等.PiN二极管的一种改进型PSpice模型［J］.电工技术学报，2011，26（增1）:172-176.

Li Fangzheng，XuQinfu，LaiJianjun，etal.An improvedpowerPiNdiodemodelforPSpice［J］. Transactions of China Electrotechnical Society，2011，26（S1）:172-176.

［15］Wang Jianjing，ChungHenryShu-Hung.Impactof parasitic elements on the spurious triggering pulse in synchronous buck converter［J］.IEEE Transactions on Power Electronics，2014，29（12）:6672-6685.

［16］ 孙凯，陆珏晶，吴红飞，等.碳化硅MOSFET的变温度参数建模［J］.中国电机工程学报，2013，33 （3）:37-43.

Sun Kai，Lu Juejing，Wu Hongfei，et al.Modeling of SiC MOSFET with temperature dependent parameters［J］. Proceedings of the CSEE，2013，33（3）:37-43.

［17］Wang Jianjing，Chung Henry Shu-hung，Li River Tinho.Characterization and experimental assessment of the effects of parasitic elements on the MOSFET switching performance［J］.IEEETransactionsonPower Electronics，2013，28（1）:573-590.

巴腾飞男，1989年生，硕士研究生，研究方向为电力电子与电力传动。

E-mail:13121384@bjtu.edu.cn

李艳女，1977年生，博士，讲师，研究方向为直流变换器软开关和光伏逆变器。

E-mail:liyan@bjtu.edu.cn（通信作者）

The Effect of Parasitic Parameters on Gate-Source Voltage of SiC MOSFET

Ba TengfeiLi YanLiang Mei
（School of Electrical EngineeringBeijing Jiaotong UniversityBeijing100044China）

In order to analyze the effect of parasitic parameters on the gate-source voltage of SiC MOSFET in the switching transient process，the model of SiC MOSFET turn-on and turn-off process is established based on the synchronous Buck converter in this paper.The effect of parasitic parameters is verified through comparing the experimental measurements with the simulation results，and is also analyzed in this paper.

SiC MOSFET，parasitic parameters，switching model，gate-source voltage

TM85

2015-04-07改稿日期 2015-10-11