基于双级矩阵变换器的变速恒频电源系统的稳定性分析及其改善措施
2016-08-10秦显慧刘晓宇雷家兴江苏省新能源发电与电能变换重点实验室南京航空航天大学南京210016
秦显慧 周 波 刘晓宇 雷家兴 韩 娜(江苏省新能源发电与电能变换重点实验室(南京航空航天大学) 南京 210016)
基于双级矩阵变换器的变速恒频电源系统的稳定性分析及其改善措施
秦显慧周波刘晓宇雷家兴韩娜
(江苏省新能源发电与电能变换重点实验室(南京航空航天大学) 南京210016)
基于双级矩阵变换器(TSMC)的变速恒频电源系统具有效率高、功率密度高、可靠性高和使用寿命长等诸多优点,在航空电源系统中具有广阔的应用前景。但受输入滤波器欠阻尼振荡的影响,基于TSMC的电源系统存在稳定性差的问题。本文讨论了输出侧LC滤波器和输出电压闭环对系统稳定性的影响,在输出电压双闭环的基础上,提出一种基于输入侧电容电压微分前馈的新型有源阻尼算法,改善了系统的稳定性。在定频和变频输入的条件下,实验结果均验证了该算法的有效性和可行性。
双级矩阵变换器变速恒频稳定性有源阻尼算法
0 引言
以空客A380和波音787为代表的现代大型客机都趋于采用体积小、重量轻且可靠性高的变频交流电源系统作为主电源[1,2]。由于航空电源系统中相当一部分负载仍需恒频供电[3],变速恒频(Variable Speed Constant Frequency,VSCF)变换器在航空电源中仍不可或缺。矩阵变换器(Matrix Converter,MC)能直接实现交-交变换,无需储能电容,因此体积重量小、可靠性高且使用寿命长[4-8]。双级矩阵变换器(Two Stage MC,TSMC)在传统MC优势的基础上[9,10],还具有无需四步换流、钳位电路简单、整流级可实现零电流开关[11]的优点,其应用技术得到了广泛而深入的研究。基于TSMC的VSCF电源系统在航空电源中拥有广阔的应用前景。
基于TSMC的VSCF电源系统需要接入LC滤波器以滤除高频纹波,提高输入性能。然而,LC滤波器容易引起系统不稳定。现有文献一般认为:在恒功率负载或可视为恒功率负载的工况下,MC或TSMC的输入端将形成负阻抗特性,极易受到电源电压波动和负载扰动的影响,在LC回路中产生谐振,导致系统失稳[12-14]。国内外学者针对这种不稳定现象,做了很多研究工作,并提出了许多增加阻尼、改善稳定性的方法。这些方法大致可分为两大类:一类是被动式阻尼,如在输入滤波电感或滤波电容两端并联阻尼电阻[15],虽简单易行,但降低了变换器效率,在航空电源的高频工作条件下,阻尼电阻的损耗更为严重。另一类是主动式阻尼,也称为有源阻尼,有多种实现方式。其中一种是数字滤波算法[16,17],控制器将采样得到的电容电压经过数字低通滤波后作为调制算法的参考值,以避免谐波信号对调制过程产生不利影响,采用锁相环技术计算输入电压相位也类似于数字滤波算法[18]。但在变频输入条件下,滤波算法将对不同输入频率产生不同程度的相移,影响控制准确度,而变频锁相环也较难实现。另一种是谐波信号前馈型算法,提取输入电压的谐波分量,以一定的比例前馈至控制器中的某一环节,通过不同的方式改变系统闭环传递函数的零极点位置,改善其稳定性。如文献[19]提出将电压谐波分量前馈至整流级调制电流矢量的参考值中。文献[20]提出将谐波分量前馈至逆变级调制电压矢量的参考值中。文献[21]则提出将谐波分量前馈至输出侧电流预测控制的电流参考值中。还有其他类型的有源阻尼策略,如文献[22]提出了一种输入电流和输出电流闭环控制相互结合的方法,也能抑制系统振荡,但其实现方法过于复杂。
从现有文献看来,谐波分量前馈型有源阻尼具有算法简单有效,方式灵活多样,适用于PI、电流预测等不同控制方法的优点,实际应用意义较高。但现有研究多是针对MC或TSMC带电机负载的稳定性和有源阻尼策略。而在对电压性能要求较高的VSCF电源系统中,通常还需要在输出侧接入LC滤波器,并对输出电压作闭环控制。在这种情况下,现有的有源阻尼算法是否仍然适用,尚未得到有效的分析和验证。
本文在现有研究的基础上,对基于TSMC的VSCF电源系统的稳定性问题及其改善策略展开研究。首先介绍了基于TSMC的VSCF电源系统拓扑结构及其双闭环控制器结构;随后分析了传统谐波分量前馈算法在输出侧PI双闭环控制的条件下,无法有效改善系统稳定性的原因;最后提出了一种采用输入侧电容电压微分前馈的新型有源阻尼算法,并通过实验验证了该算法的有效性和可行性。
1 基于TSMC的VSCF电源系统
图1所示为基于TSMC的VSCF电源系统拓扑结构。TSMC的输入端接入的电源为航空发电机所产生的一次电源,即变频交流电源;输出端为恒压恒频400 Hz三相交流电压。输出、输入侧均接入LC滤波器以滤除输出电压和输入电流中的高频纹波。
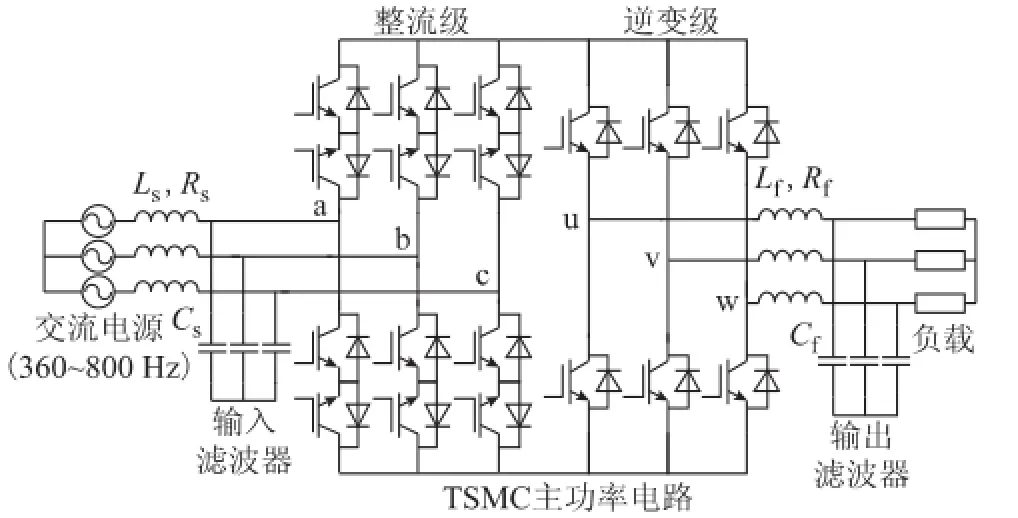
图1 基于TSMC的VSCF电源系统拓扑结构Fig.1 Diagram of TSMC-based VSCF generation system
1.1TSMC的基本调制方式
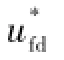
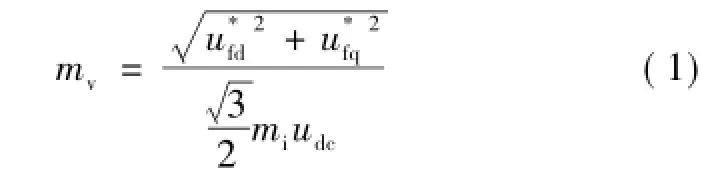
式中,udc为直流母线平均电压。
1.2基于dq坐标系的输出电压双闭环控制
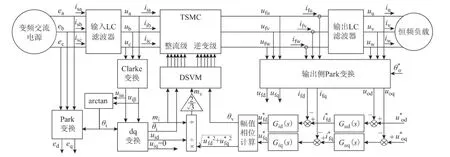
图2 基于TSMC的VSCF电源系统的调制和闭环控制原理框图Fig.2 Diagram of modulation and close-loop control of TSMC-based VSCF generation system
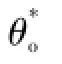
根据典型Ⅱ型系统的工程设计方法[26]设计内、外环PI控制器的传递函数为

式中,Lf为输出滤波电感;Rf为等效内阻;Cf为输出滤波电容;τ为电流环闭环传递函数的等效时间常数,τ=2T;h为中频宽度,折中考虑控制器响应速度和超调量,取h=5。
1.3输出滤波器对系统控制稳定性的影响
设电源电压dq轴分量为ed、eq;电源电流isa、isb和isc的dq轴分量为isd、isq;TSMC输入端电流iia、iib和iic的dq轴分量为iid、iiq。则输入侧LC滤波器的电路方程为
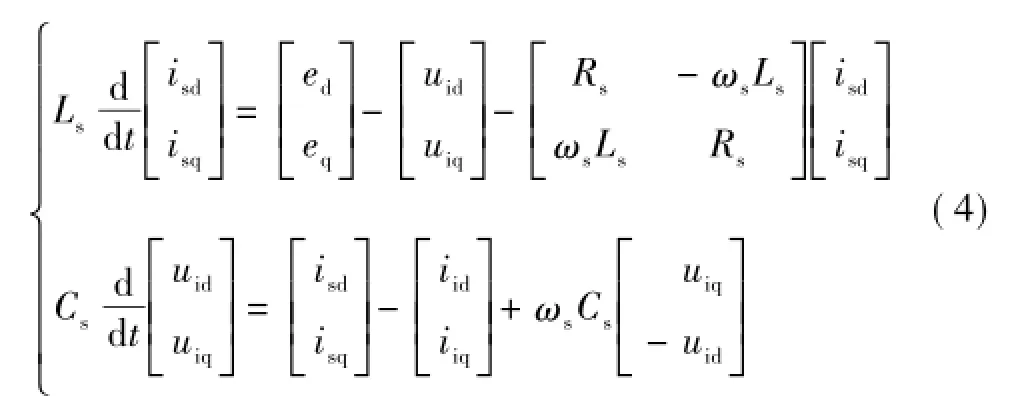
一般地,空间矢量调制的输入电流矢量与电容电压矢量保持同相位,因而iiq=0;同时,忽略iid、iiq和ufd、ufq的高频分量,根据TSMC输入输出侧瞬时功率相等的原则,即uidiid+uiqiiq=ufdifd+ufqifq,可知
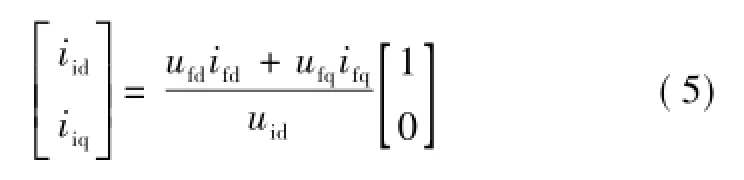
ufd、ufq是TSMC输出端电压,在调制过程中可能存在突变,直接根据式(4)分析输入电流的特性,存在一定难度。而根据输出侧LC滤波器的电路方程,可知ufd、ufq与负载端电压uod、uoq存在关系
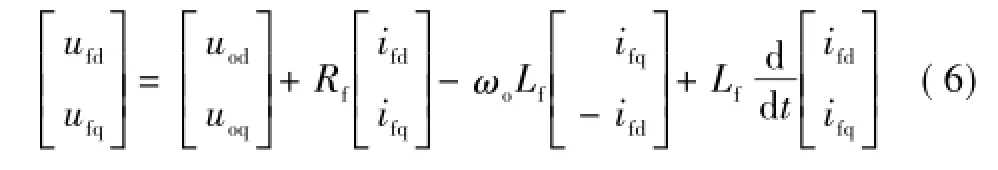
将式(6)代入式(5),可得输入电流与输出电流的关系为
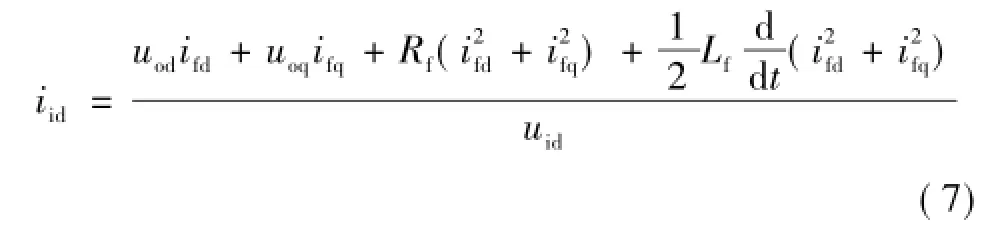
输出电压达到稳态时,输出电压dq轴分量与给定值基本一致,因而可认为 uoq=0,而 uodifd项是式(7)等式右边的主要部分,忽略其他次要部分,则

由于输出侧滤波器具有平抑uod和ifd瞬时波动的作用,uodifd项在稳态时可视为恒定。由此可知,与文献[21,22]中TSMC输出侧直接连接电机负载或RL负载的情况类似,TSMC输出侧通过LC滤波器连接负载并对输出电压做闭环控制时,也可视为恒功率负载,因而在输入端呈现负阻抗特性,系统易出现振荡失稳的现象。
2 传统谐波分量前馈算法的稳定性分析
设Δx表示变量x的谐波分量,而Uid、Uod和Ifd分别表示uid、uod和ifd的稳态直流分量,则输入侧LC滤波器的d轴谐波分量等效模型如图3所示。而根据式(8),可得TSMC输出电流与输入电流谐波分量的关系为

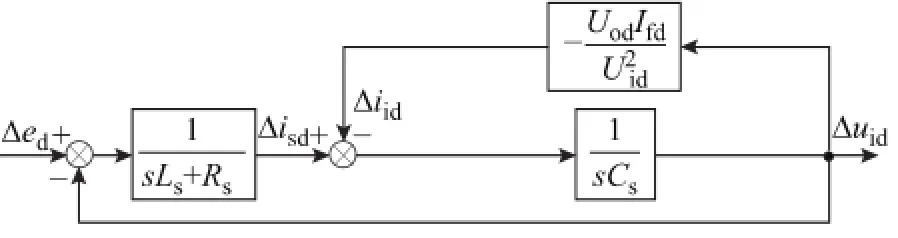
图3 输入侧LC滤波器的d轴谐波分量等效模型Fig.3 Equivalent model of d-axis harmonic components of the input filter
谐波分量前馈算法的基本思路是通过将Δuid前馈至控制器的某一环节,迫使Δifd发生变化,Δiid也随之变化,抑制Δuid的振荡,从而实现有源阻尼。
2.1谐波分量前馈至调制电压参考值
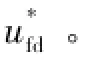
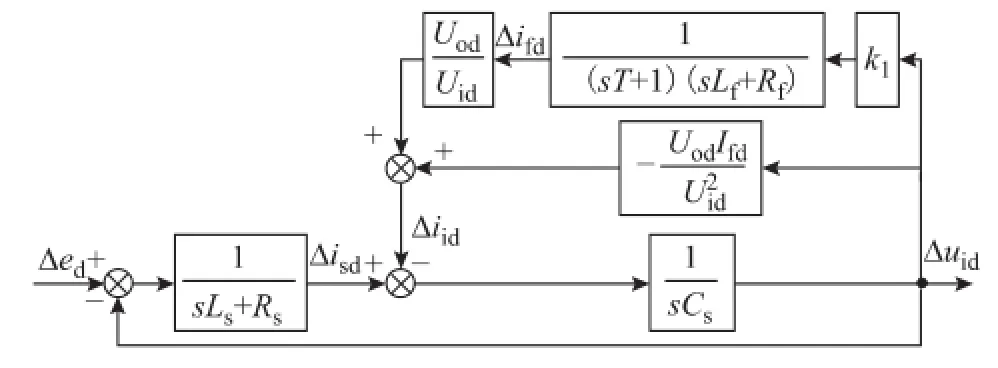
图4 Δuid前馈至输入滤波环节的d轴谐波分量等效模型Fig.4 Equivalent model of d-axis harmonic components of the input filter with Δuidfeeding to
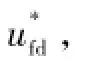
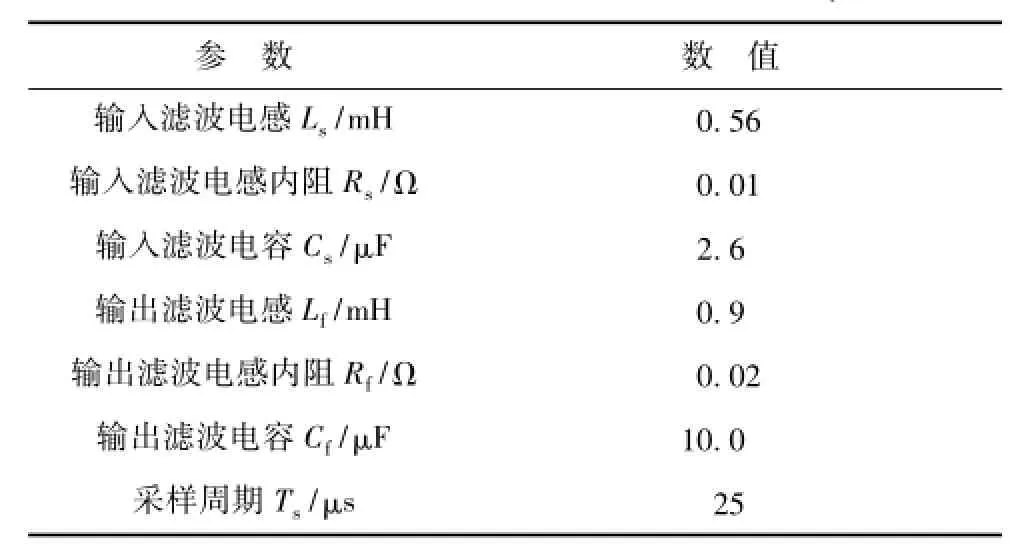
表1 基于TSMC的VSCF电源系统相关参数Tab.1 Parameters of the TSMC-based VSCF system
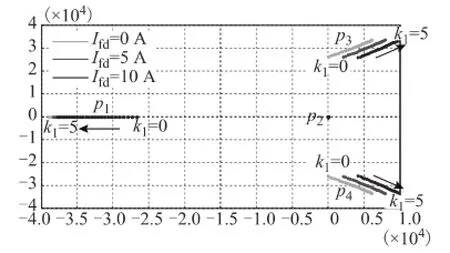
图5 Δuid前馈至输入滤波环节的根轨迹Fig.5 Root-locus of input filter with Δuidfeeding to
这种方法在TSMC输出侧直接连接RL负载时稳定,而在输出侧连接LC滤波器时不稳定的原因在于,滤波器的内阻远远小于负载电阻,两种输出形式下系统极点的分布规律不同。若将Rf增大至5 Ω,则图5中的极点p3和p4可随着k1的增大而进入左半平面,使系统趋于稳定。但这也从侧面验证了文献[21]的有源阻尼算法有一定的局限性,即负载电阻不能太小,否则该算法无效。
2.2谐波分量前馈至电流内环参考值
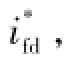
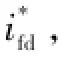
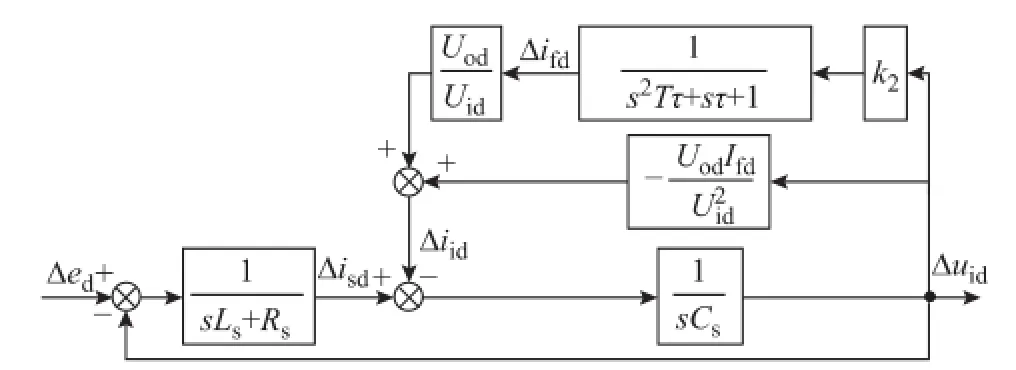
图6 Δuid前馈至输入滤波环节的d轴谐波分量等效模型Fig.6 Equivalent model of d-axis harmonic components of the input filter with Δuidfeeding to
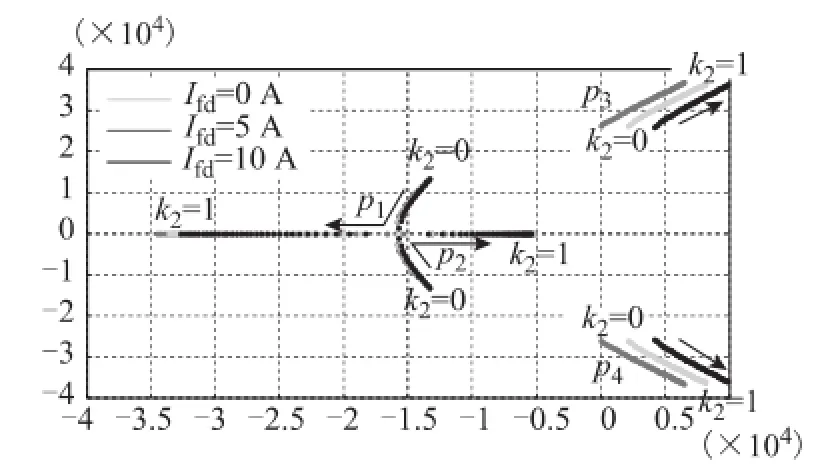
图7 Δuid前馈至输入滤波环节的根轨迹Fig.7 Root-locus of input filter with Δuidfeeding to
该方法在输出侧电流内环为速度更快的预测电流控制时,输入电流能快速响应谐波分量前馈的信号,系统的阻尼可得到一定的改善。但是电流预测控制方法必须先建立输出电流对输出电压的响应模型,对系统参数有一定的依赖性,而且在硬件实现上也有一定难度,实用性不强。
3 基于电压微分前馈的有源阻尼算法
通过第1节的分析可知,由于VSCF电源系统的输出侧是LC滤波器,而且控制上采用PI双闭环结构,传统的谐波分量前馈方法,不管馈送至哪个环节,都无法有效改善TSMC控制系统的稳定性。
针对这个问题,本文提出一种新型有源阻尼算法,将Δuid的微分量前馈至电流内环的参考值,则基于微分前馈的新型有源阻尼算法如图8所示。而且由于uid直流分量的微分值为零,所以本算法无需将谐波信号从uid中提取出来,可直接将uid的微分作为前馈信号。采用微分前馈,输入侧滤波器的d轴谐波分量等效模型则转变为图9的形式,其闭环传递函数Φd(s)为

其中
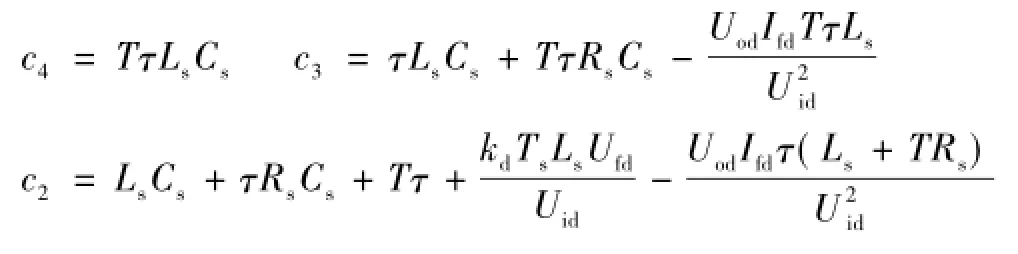
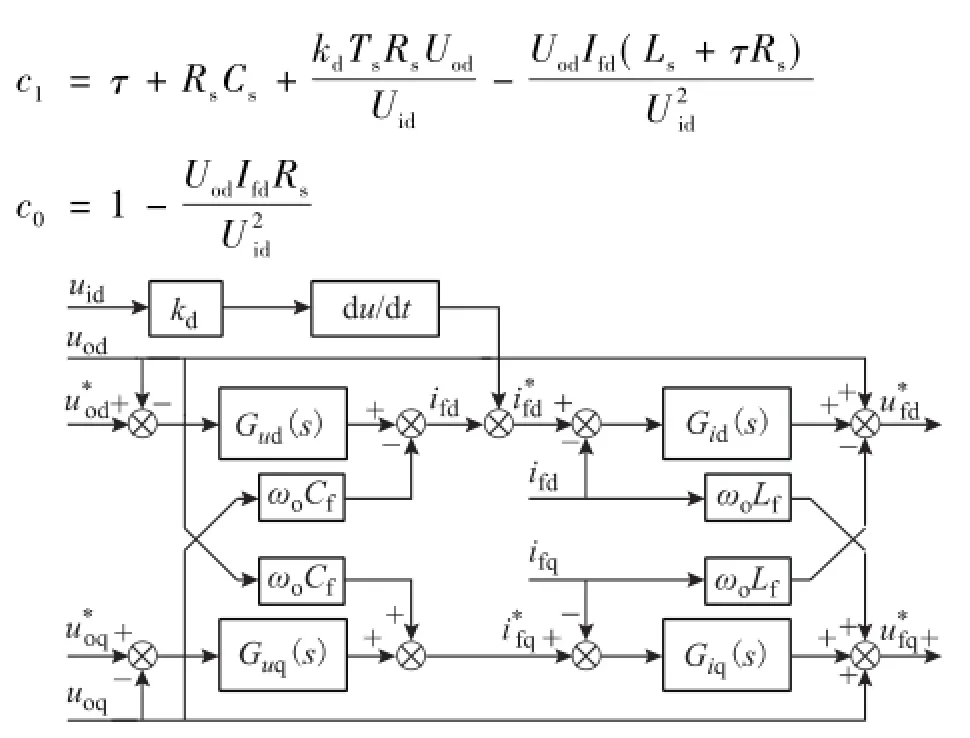
图8 基于微分前馈的新型有源阻尼算法Fig.8 Diagram of the novel active damping algorithm based on derivative feed-forward
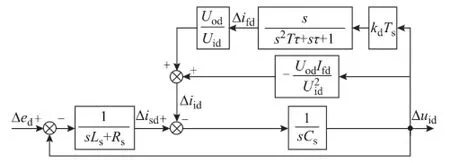
图9 采用微分前馈,输入侧滤波器d轴谐波分量等效模型Fig.9 Equivalent model of d-axis harmonic components of the input filter with derivative feed-forward
在不同的负载条件下,令微分前馈系数kd从0增大至1,采用微分前馈,输入滤波环节的闭环根轨迹如图10所示。从图10中可以看出,微分前馈的加入,能使原本处于虚轴附近或右半平面的极点p3、p4向左半平面移动,而左半平面的极点p1、p2仍保持在左半平面,从而使TSMC控制系统趋于稳定。
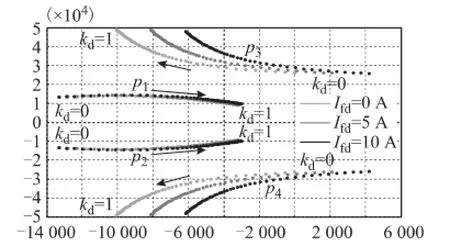
图10 采用微分前馈,输入滤波环节的闭环根轨迹Fig.10 Root-locus of input filter with derivative feed-forward
从图10中还可发现,不同负载条件下,能使全部极点都进入左半平面的kd值有所不同,但kd值的选择具有单调性,即只要输出功率最大时系统稳定,功率较小时,系统也就能保持稳定。不过,由于uid信号中不可避免地存在一些高频纹波和噪声干扰,kd的值也不宜过大,否则纹波、噪声信号通过微分环节放大,也对系统的稳定性有不利影响。
4 实验
本文建立了一套TSMC的硬件实验平台,用以模拟VSCF电源系统。实验平台主功率电路的整流级采用APTGF50TDU120模块搭建,逆变级采用分列器件FGA25N120ANTD,控制器采用DSP和CPLD联合实现,其型号分别为TMS320F28335和LC5512,同时采用外扩的ADS8568高性能模数转换芯片采样电压电流信号,以保证微分环节的可靠性。TSMC的输入、输出滤波元件参数与表1完全一致,通过Chroma61511可编程交流电源提供360~800 Hz三相交流电压源,输入相电压有效值为110 V,输出相电压有效值的闭环给定值为55 V。采用1.25 kV·A的RL负载作为测试条件,负载电阻为6.88 Ω,电感为1.9 mH。根据根轨迹图,选择微分前馈系数为kd=0.137。
首先,选择定频600 Hz输入,记录输出电压阶跃响应的实验波形如图11所示,其中图11a为无阻尼的实验波形,图11b为采用了本文所提出的微分前馈算法后的有源阻尼实验波形。从图11a中可以明显看出,在无阻尼的情况下,由于系统不稳定,d轴电压分量存在明显的高频振荡,而采用微分前馈算法后,振荡得到了有效的抑制,而阶跃响应的动态过程(超调量、调节时间)基本不变。
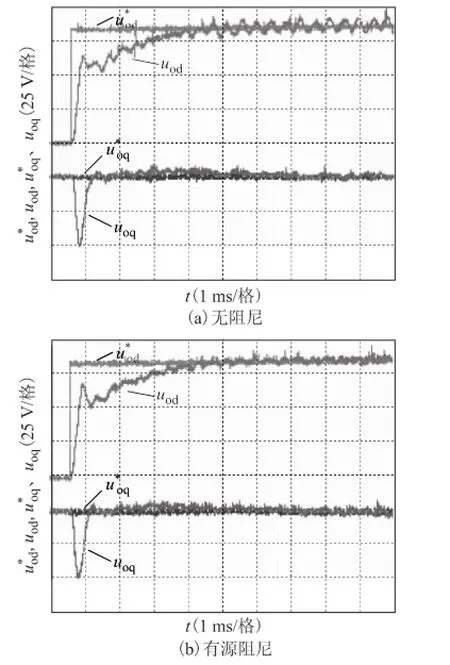
图11 输出电压阶跃响应的实验波形Fig.11 Ste PResponse of output voltage
稳态时a相输入相电压、相电流和输出u相的相电压、相电流的波形如图12所示,其中图12a为无阻尼时的实验波形,输出电压含有谐振分量,同时输入侧电容电压和输入相电流存在明显的振荡和畸变。图12b为采用微分前馈算法后的有源阻尼实验波形,输入电压电流和输出电压电流波形的正弦度良好,波形质量高,控制器的稳态性能得到大幅提高。
其次,设定输入频率以约40 ms的周期在360~800 Hz之间快速变化,变频输入下,稳态时输入输出电压电流波形如图13所示,可以看出,微分前馈算法在变频输入的条件下同样具有良好的阻尼效果,验证了本文所提出算法的可行性、有效性和可靠性。

图12 稳态时输入输出电压电流波形Fig.12 Steady-state waveforms of I/O voltage and current
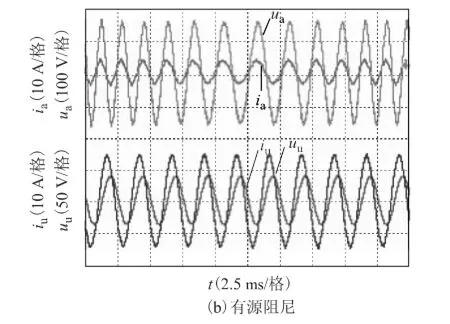
图13 变频输入下,稳态时输入输出电压电流波形Fig.13 Steady-state waveforms of I/O voltage and current with varying input frequency and without damp
5 结论
本文针对基于TSMC的VSCF电源系统展开了研究,分析了TSMC的稳定性问题,在对比现有阻尼算法的基础上,提出了一种基于微分前馈的新型有源阻尼算法。通过本文的研究得到以下结论。
1)TSMC输出侧接入LC滤波器,并采用dq坐标系下的PI双闭环控制结构时,其输出侧仍然可视为一个恒功率负载,并可据此分析出TSMC的控制系统具有不稳定性。
2)传统的谐波分量前馈型有源阻尼算法多是针对电机负载或RL负载提出的,在TSMC输出侧连接LC滤波器的条件下并不适用,无法有效改善系统的稳定性。
3)采用本文提出的基于输入侧电容电压微分前馈的有源阻尼算法,可有效提高控制系统的稳定性,同时几乎不影响输出电压闭环控制的动态和稳态性能。而且该算法无需分析谐波分量和基波分量,具有较高的实用性。其有效性和可行性在定频和变频输入的条件下都得到了实验验证。
附录
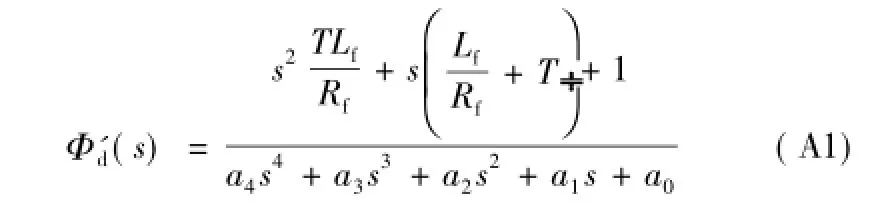
其中
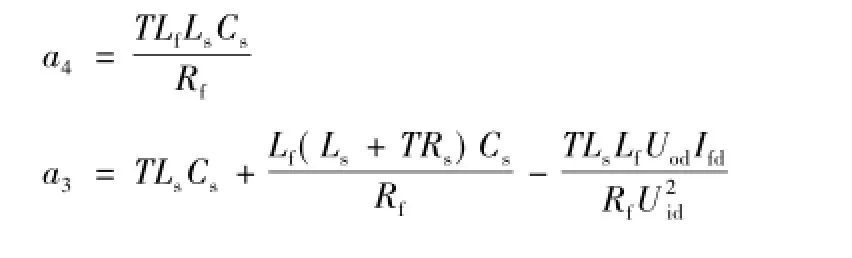

其中
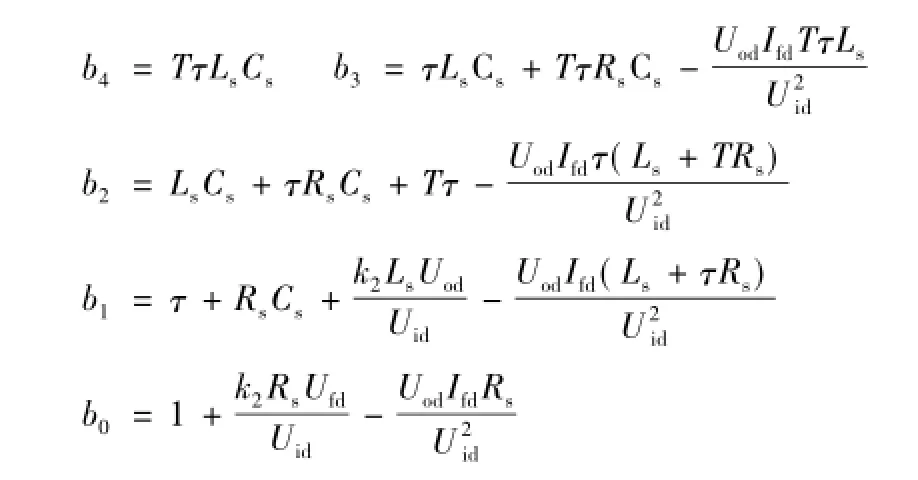
[1]Cao W P,Mecrow B,Atkinson G,et al.Overview of electric motor technologies used for more electric aircraft (MEA)[J].IEEE Transactions on Industrial Electronics,2012,59(9):3523-3531.
[2]杨善水,张卓然,杨春源,等.基于多环调压控制的混合励磁航空变频交流发电系统[J].电工技术学报,2012,27(3):176-180.
Yang Shanshui,Zhang Zhuoran,Yang Chunyuan,et al.Aeronautic variable frequency AC generation system based on multi-loop controlled voltage regulator[J]. Transactions of China Electrotechnical Society,2012,27(3):176-180.
[3]ChangJ,WangAH.NewVF-powersystem architecture and evaluation for future aircraft[J].IEEE Transactions onAerospaceandElectronicSystems,2006,42(2):527-539.
[4]夏长亮,阎彦.矩阵变换器-永磁同步电机系统[J].电工技术学报,2015,30(23):1-9.
Xia Changliang,Yan Yan.Matrix converter-permanent synchronous motordrives[J].TransactionsofChina Electrotechnical Society,2015,30(23):1-9.
[5]Kolar J W,Friedli T,Rodriguez,et al.Review of three-phase PWM AC-AC converter topologies[J].IEEE Transactions on Industrial Electronics,2011,58(11): 4988-5006.
[6]陆松,葛红娟,陈思,等.基于滤波器状态反馈的矩阵变换器网侧电流闭环策略[J].电工技术学报,2016,31(7):65-71.
Lu Song,Ge Hongjuan,Chen Si,et al.A grid current closed-loop control strategy for matrix converter based on states feedbackoffilter[J].TransactionsofChina Electrotechnical Society,2016,31(7):65-71.
[7]Kobravi K,Iravani R,Kojori H A.A review and implementationofmatrix-converterforaerospace application[C]//Proceedings of IEEE Energy Conversion CongressandExposition,Raleigh, USA,2012: 698-705.
[8]Friedli T,Kolar J W,Rodriguez J,et al.Comparative evaluation of three-phase AC-AC matrix converter and voltage DC-linkback-to-backconvertersystems[J]. IEEE Transactions on Industrial Electronics,2012,59 (12):4487-4510.
[9]TrentinA, ZanchettaP, WheelerP, etal. Performance assessment of matrix converter and two stage matrix converter for EMA in aircraft application[C]// Proceedings of Power Electronics Specialists Conference,Rhodes,Greece,2008:2692-2697.
[10]Wei LX,LipoTA,ChanH.Matrixconverter topologieswithreducednumberofswitches[C]// Proceedings of IEEE 33rd Annual Power Electronics Specialists Conference,Cairns,Australia,2002:57-63.
[11]史婷娜,安少波,阎彦,等.超稀疏矩阵变换器窄脉冲抑制[J].电工技术学报,2015,30(14):247-252.
Shi Tingna,An Shaobo,Yan Yan,et al.Narrow pulse suppressionforultrasparsematrixconverter[J]. Transactions of China Electrotechnical Society,2015,30(14):247-252.
[12]Wang J,Bouazdia M.Influence of filter parameters/ topologies on stability of matrix converter-fed permanent magnet brushless motor drive systems[C]//Proceedings of IEEE International Electric Machines and Drives Conference,Miami,USA,2009:964-970.
[13]Guan Q,Yang P,Wang X,et al.Stability analysis of matrix converter with constant power loads and LC input filter[C]//Proceedingsof7thInternationalPower Electronics and Motion Control Conference,Harbin,China,2012,2:900-904.
[14]Rahimi M,Emadi A.Active damping in DC/DC power electronic converters:a novel method to overcome the problems of constant power loads[J].IEEE Transactions on Industrial Electronics,2009,56(5):1428-1439.
[15]She H,Lin H,Wang X,et al.Damped input filter designofmatrixconverter[C]//Proceedingsof International Conference on Power Electronics and Drive Systems,Taipei,China,2009:672-677.
[16]Casadei D,Serra G,Tani A,et al.Effects of input voltage measurement on stability of matrix converter drive system[J].IEEEProceedingsofElectricPower Applications,2004,151(4):487-497.
[17]Liu F,Klumpner C,Blaabjerg F.Stability analysis and experimental evaluation of a matrix converter drive system [C]//Proceedings of IECON,Roanoke,USA,2003: 2059-2065.
[18]Ruse J,Clare J,Klumpner C.Numerical approach for guaranteeing stable design of practical matrix converter drives systems[C]//Proceedings of IECON,Paris,France,2006:2630-2635.
[19]Shi M,Zhou B,Wei J,et al.Design and practical implementation ofanovelvariable-speedgeneration system[J].IEEE Transactions on Industrial Electronics,2011,58(11):5032-5040.
[20]Sun Y,Su M,Li X,et al.A general constructive approach tomatrixconverterstabilization[J].IEEE TransactionsonPowerElectronics,2013,28(1): 418-431.
[21]Rivera M,Rojas C,Rodriguez J,et al.Predictive current control with input filter resonance mitigation for a direct matrix converter[J].IEEE Transactions on Power Electronics,2011,26(10):2794-2803.
[22]Haruna J,Itoh J.Control strategy for a matrix converter with a generator and a motor[C]//Proceedings of APEC,Fort Worth,USA,2011:1782-1789.
[23]Rodriguez J,Rivera M,Kolar J W,et al.A review of control and modulation for matrix converters[J].IEEE Transactions on Industrial Electronics,2012,59(1): 58-70.
[24] 张晋颖.基于重复控制和PI双闭环控制的三相四桥臂逆变器[D].秦皇岛:燕山大学,2006.
[25] 张崇巍,张兴.PWM整流器及其控制[M].北京:机械工业出版社,2002.
[26] 陈伯时.电力拖动自动控制系统——运动控制系统[M].北京:机械工业出版社,2003.
周波男,1961年生,博士,教授,博士生导师,主要从事风力发电、航空电源系统、电机及其控制技术的研究。
E-mail:zhoubo@nuaa.edu.cn
Stability Analysis and Improving Strategies for Two Stage Matrix Converter-Based Variable Speed Constant Frequency Power System
Qin XianhuiZhou BoLiu XiaoyuLei JiaxingHan Na (Jiangsu Key Laboratory of New Energy Generation and Power ConversionNanjing University of Aeronautics and AstronauticsNanjing210016China)
The variable speed constant frequency(VSCF)power system based on two stage matrix converter (TSMC)has advantages in efficiency,power density,reliability,and lifetime.Thus,it earns a broader application prospect in the aero power system.However,the TSMC often suffers from instability due to the underdamped oscillation of the input filter.In this paper,the influence of the output filter as well as the output voltage close-loop control upon the system stability is discussed.And a novel active damping algorithm based on the derivative feedforward of the input voltage is proposed to improve the system stability.Experiments verified the feasibility and validity of the proposed algorithm with both fixed and variable input frequencies.
Twostagematrixconverter,variablespeedconstantfrequency, stability,active damping algorithm
秦显慧男,1988年生,博士,研究方向为电力电子与电力传动。E-mail:shayslmc@aliyun.com(通信作者)
TM91
国家自然科学基金(51177069)和江苏省高校优秀科技创新团队资助项目。
2015-10-24改稿日期 2016-04-17
