基于启发式算法的飞机指派优化模型及算法
2016-08-10贾宝惠
刘 婧, 贾宝惠
(1.新疆大学 电气工程学院,新疆 乌鲁木齐 830047;2.中国民航大学 航空工程学院,天津 300300)
基于启发式算法的飞机指派优化模型及算法
刘婧1,贾宝惠2
(1.新疆大学 电气工程学院,新疆 乌鲁木齐830047;2.中国民航大学 航空工程学院,天津300300)
摘要:安全与经济是航空公司运营中互相矛盾的两个因素,安全性提高必然导致运行成本的增加。首先,综合考虑飞机航班任务与例行检修任务,建立了飞机指派优化模型,使飞机的飞行时间尽可能接近飞机的期望飞行时间;其次,为了求解该模型,设计了基于专家规则的启发式算法,快速实现了多任务分配的优化飞机指派计划;最后,采用某航空公司的实际航班数据,进行了算例分析,并与采用蚁群算法进行优化的结果进行了比较,说明了该模型和算法的合理性。
关键词:飞机排班; 优化模型; 例行检修; 启发式算法
1引言
飞机排班是航班计划中的一部分,它需要根据航班计划要求、飞机机型特征与技术状态等因素为每一架飞机分配每天的航班飞行任务和必要的检修任务,从而保证航班任务顺利进行。因此,如何高效并合理的制定飞行计划,提高飞机利用率和利润是航空公司在竞争中取胜的重要因素。
国内外很多学者在这方面做了大量的研究工作。Rexing[1]等提出了“时间窗”的概念,建立了机型指派和航班时刻的综合模型;Rosenberger[2]与Sriram[3]等人分别研究了动态的机型指派问题以及不正常航班下飞机计划恢复中的机型调整问题等。Erling与Gronkvist[4]等建立飞机指派约束编程(Constraint Programming)模型,并提出了列生成等算法;朱星辉[5]等人对周机型指派问题的研究;孙宏、杜文[6]等学者将飞机指派问题划分为三个方面,即基于飞机调度指令要求、基于最少需用飞机数、基于飞机使用均衡要求的飞机排班问题及求解算法;李耀华[7]等主要考虑航站衔接及过站时间衔接的约束条件,建立了航班串的优化模型,并构造了一种自适应遗传算法。
上述研究均未考虑飞机技术状态因素,因此不能合理安排例行检修任务,导致检修次数和航班运营成本的增加。本文在例行检修的约束下,以飞机使用均衡为目标,使飞机的飞行时间尽可能接近飞机的期望飞行时间,建立多任务分配的飞机排班优化模型,采用基于专家规则的启发式算法,完成航班任务和例行检修任务的分配,使机队中每架飞机的周飞行时间尽量接近期望的飞行时间。
2飞机排班问题分析
2.1飞机排班问题分析
飞机排班中需要考虑的基本约束有以下几点:(1)满足航班计划要求,即航班属性与相应执飞飞机保持一致;飞机执行航班节到站机场与出发机场一致;以及航班过站时间不得小于最小衔接时间。(2)满足唯一性要求,即每个航班应当且仅能安排一架飞机执行,每架飞机在同一时段最多只能执行一个航班。(3)满足相互匹配的要求,主要是指执飞飞机应满足航班属性要求,如高原航班所对应的飞机必须能飞高原,以及不给临近停场维修的飞机分配航班任务。
2.2例行检修约束分析
例行检修约束作为飞机排班的一个重要约束条件,对安全飞行起着关键作用。通常以飞行时间为检修间隔的单位。根据适航条例,令M为检修级别集合(检修级别一般分为A检,B检,C检),对任意m∈M,规定飞机在任意两次检修之间飞机的累计飞行时间不得大于检修间隔时间。
3飞机排班优化模型
为了清晰地描述模型,本文引入检修节点、虚拟飞机节点、剩余飞行时间[8]来表示检修任务的变量,建立多任务分配的飞机排班数学模型。
检修节点Vm为指完成上次飞行任务后,飞机的停留机场可执行检修m或航班任务的最后到达机场可执行检修m的点的集合。
虚拟飞机节点vfc为表示飞机完成检修后,可以继续执飞航班,即上一次检修完成时刻与下一班航班起飞时间的间隔时间大于或等于最小过站时间。
根据上述定义[8]将飞机c执飞航班至vi后,检修m的累计飞行时间累计飞行时间定义为
(1)
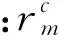
飞机排班的优化模型描述如下
(2)
s.t.
(3)
(4)
(5)
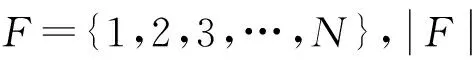
其中式(2)为目标函数,表示某架飞机实际飞行时间与期望飞行时间的差值最小;式(3)是流平衡约束,xij为决策变量,即飞机执行完航班i后执行航班j则xij=1;否则值为0;公式(4)是满足例行检修约束。
模型以满足基本飞机指派约束为基础,以实现飞机的飞行时间最大程度的接近飞机计划时间为目标[6]。对于临近停厂检修的飞机,对其实际飞行时间的限制比较严格,而对于其他飞机,通常情况下采用均衡排班的原则,即每架飞机本周的实际飞行时间尽可能平均。为了简化模型的陈述,考虑没有飞机临近检修,此时所有飞机的期望飞行:
(6)
这里假设已得到航班计划,即将一周的航班分成了与飞机数A相匹配的a组。即将飞机指派问题转化为飞机对航班环的分配问题。即对于一个排班周期内(一般为7天)每一天的a个航班组,分别指定给a架飞机,使得在此排班周期内,每架飞机都尽可能的接近其计划飞行时间。
4算法设计
4.1路径搜索规则
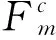
假设模型中所有飞机均不考虑临近停厂维修的特殊情况,设计搜索路径为一个周一的航班连接一个周二的航班再连接一个周三的航班,依次到周日,再返回连接一个周一的航班,依次以7为周期循环。由此可满足流平衡约束。
4.2对调优化的决策规则
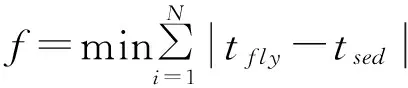
5仿真研究
为了验证飞机指派优化模型及算法,这里采用某航空公司一个机队10架飞机与70个航班环进行仿真研究。假设每架飞机的日飞行时间为3到10个小时不等,我们对每个航班环随机生成一个 210(min)到 600(min)之间的整数,代表空中飞行时间(分钟)。
初始数据如表1所示,其中第一列代表了飞机的机号,第二列到第八列代表了随机产生的航班环的空中飞行时间,第九列代表的是某一架飞机一周执行的航班环的飞行时间,最后一列代表的是每架飞机的期望飞行时间。
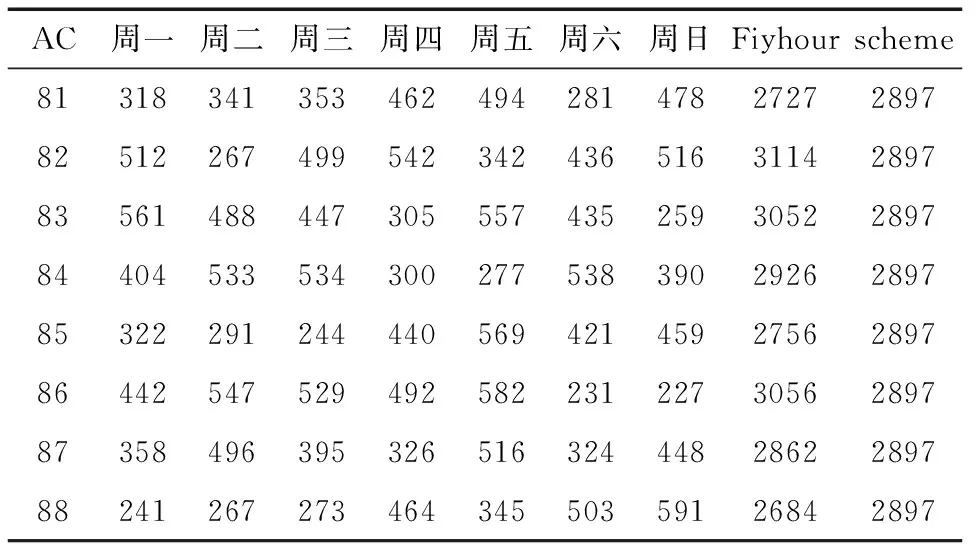
表1 初始数据Tab.1 Intial data
经过算法求解后,得到优化后的排班结果如图1所示。为了便于检验,这里将程序做成了可视文件,运行结果截图2所示。

图1 启发式算法运行的飞机指派结果Fig.1 Aircrqft assignment reshlts bas on heuristic algonithm
本文以最小代价(每架飞机周飞行时间与期望飞行时间的均方根)来评价所得排班结果的优化程度,引入最小代价的概念,即
根据上图,计算其最小代价为:
由上图可以看出,排序前机队内每架飞机的周飞行时间与期望飞行时间的差值差异较大,飞机B2的周飞行时间超过期望飞行时间较多,这有可能导致飞机提前进入检修时间,增加维修成本,而飞机B8的周飞行时间离期望飞行时间相差较远,这就是说,该飞机资源没有得到充分的利用,降低了航空公司的运营利润;经过算法处理排序后,每架飞机的周飞行时间都以期望飞行时间为基准波动,且波动很小。达到了预期的目的,使得飞机的飞行时间尽可能的接近期望飞行时间。使每架飞机资源都得到充分的利用,提高了航空公司的经济利润。
下面是其他学者用蚁群算法[8]求解该问题时得到的结果,如表2所示。

表2 基于蚁群算法运行的飞机指派结果Tab.1 Aircraft assignment results borsed on ant colony algorithm
根据该表格中的数据,计算其最小代价为
与本文中启发式算法所得的最小代价为3.99相比,明显地看出本文设计的启发式算法的优化效果
6结束语
本文在分析飞机排班的工作流程的基础上,建立了飞机指派的优化模型,在满足飞行安全的前提下使飞机得使用飞行时间尽可能的接近飞机计划飞行时间,充分利用飞机资源,实现航空公司经济效益最大化。采用基于专家规则的启发式算法实现了快速求解,通过实际数据进行仿
真研究,结果表明:本文建立的模型和算法切实可行,可动态快速的进行飞机指派,从而提高航空公司生产调度的自动化水平。
参考文献:
[1]Rexing B,Barnhart C,Kniker T S.Airline fleet assignment with time windows,Transportation Science[J],2000,34(1):1-20.
[2]Sriram C,Haghani A.An optimization model for aircraft maintenance scheduling and reassignment Transportation Research Part A:Policy and Practice[J],2003;37(1):29-48.
[3]Erling G,Rosin D.Tail assignment with maintenance restrictions:a constraint programming approach[D],Chalmers University of Technology,Gothenburg,Sweden,2002.
[4]Gronkvist M.The tail assignment problem[D],Chalmers University of Technology,Gothenburg,Sweden,2005.
[5]朱星辉,朱金福,巩在武.我国航空公司机型指派模型及算法研究,工业技术经济[J],2007,26(4):75-77.
ZHU Xinghui,ZHU Jinfu,GONG Zaiwu.Research on the model and algorithm of Chinese airline model assignment,Industrial technology economy[J],2007,26(4):75-77.
[6]高强,朱星辉,李云,等.南京航空航天大学民航学院[J].武汉理工大学学报(交通科学与工程版),2012,36(1):153-157.
GAO Qiang,ZHU Xinghui,LI Yun,et al.Civil aviation college of nanjing university[J].Journal of Wuhan University of Technology(Transportation Science & Engineering),2012,36(1):153-157.
[7]李耀华,秦如如.基于混合遗传算法的航班串优化模型研究.[J]中国民航大学学报,2010,28(6):31-34
LI Yaohua,Qinruru.Research on the model of flight string optimization based on hybrid genetic algorithm[J].Journal of Civil Aviation University of China,2010,28(6):31-34.
[8]周琨,夏洪山.基于协同多任务分配的飞机排班模型与算法[J].航空学报,2011,32(12):2293-2302.
ZHOU Kun,XIA Hongshan.Aircraft scheduling model and algorithm based on Cooperative multi task assignment[J].Aeronautical Journal,2011,32(12):2293-2302.

刘婧女(1987-),新疆哈密市人,硕士研究生,主要研究方向为航空维修工程及生产计划建模及智能算法。

贾宝惠女(1971-),山西省运城人,副教授,硕士研究生导师,主要研究方向为航空维修工程及生产计划建模及智能算法、航空机电技术及维修工程。
中图分类号:TP 319.9
文献标识码:A
基金项目:国家科学基金资助项目(DMC)
Study on Optimization Model and Algorithm of flight Assignment based on Heuristic Algorithm
LIU Jing1,JIA Baohui2
(1.School of Electrical Engineering,XinJiang University,Urumqi 830047,China;2.Aeronautic Engineering College,Civil aviation university of China,Tianjin 300300,China)
Abstract:Safety and economic profit are two factors that contradict each other in the flight operation,Security improvement will inevitably lead to the increase of operating costs.First,considering the aircraft flight mission and routine maintenance tasks,established optimization model of aircraft assignment,the rate of using aircraft as a target,letting the aircraft fly time as close as possible to the expectations time;Secondly,in order to solve the model,designing an algorithm which named expert rule-based heuristic algorithm,which can quickly achieve optimized flight assigned.Finally,using actual data from an airline,completed calculation and analysis,at the same time compared with the ant colony algorithm.It has been proven that the rationality of the model and algorithm.
Key words:flight assignment; optimization model; routine maintenance; heuristic algorithm
