水下隐身动目标激光探测水面能量散射特性研究*

姚　瑶　孙晓峰　陶永勤

(海军702厂　上海　200434)



水下隐身动目标激光探测水面能量散射特性研究*

姚瑶孙晓峰陶永勤

(海军702厂上海200434)

摘要为了提高卫星对水下隐身动目标的探测效率，对不同海况下、不同入射角度时的三维激光海面漫反射特性进行了建模仿真计算，并在实验室条件下对激光入射波动水面后产生的散射场的能量分布特性进行了的研究。首先，根据麦克斯韦尔方程和边界条件对散射场在各个方向上的分量之间的耦合关系进行了研究，并列出矩阵方程;然后，利用三维锥形波对入射激光束进行了模拟;最后，通过稀疏矩阵规则网格法求解矩阵方程，得出三维双站散射系数，并通过实验对仿真结果加以验证。结果表明该方法能够准确地表示波动水面的三维激光漫反射特性，为进一步研究三维激光海面漫反射特性奠定了基础。

关键词激光; 潜艇; 无人水下自航器; 漫反射; 双站散射系数; 海面

Class NumberTN219

1引言

潜艇、UUV等水下隐身动目标具有极大的战略威慑力和极强的战场信息侦察能力，使得传统的声呐探测手段遇到了新的挑战。因此，利用绿激光对海水的穿透特性以及绿激光对水下隐身动目标特征的Mie散射效应，可以作为探潜体系的一种补充手段，以进一步提高对水下隐身动目标的探测效能。由于不同海况、不同角度入射的激光散射能量分布具有很大的差异，对于探测效率有着非常大的影响。因此，针对不同海况，得出准确的三维激光海面漫反射特性，对于提高卫星对水下隐身动目标的探测范围和准确率具有重要的意义。

由于入射激光束经过粗糙界面漫反射后，不同偏振状态的激光在各个方向上有着复杂的耦合关系。因此为了方便计算，以往求解方法大多基于一定的近似条件，如基尔霍夫近似(Kirchhoff Approach, KA)方法[1]，这些近似条件不但对粗糙面的参数有一定的限制，由于其固有的物理近似势必带来误差，使得计算结果达不到理想的效果。二维前后向迭代法(Forward-Backward Method, FBM)[2]虽然是数值计算方法，但是它是将三维的粗糙界面简化为二维界面后得出的数值模拟。由于其所建立的二维粗糙界面与现实中的粗糙界面差别很大，因此仿真计算结果的准确性较差。

因此，为了得到准确的激光在波动水面上的漫反射能量分布特性，本文采用稀疏矩阵规则网格法(Sparse Matrix Canonical Grid Method, SMCG)来计算激光在波动水面上的双站散射系数(Bistatic Scattering Coefficient, BSC)，该算法不仅减小了计算机内存的需求，而且由于在每步迭代过程中矩阵与向量的运算又采用快速傅里叶变换(Fast Fourier Transition, FFT)算法，进一步减小了CPU的计算时间。

2激光漫反射原理

假设一束激光入射到波动水面S上，则三维激光漫反射的剖面示意图如图1所示。

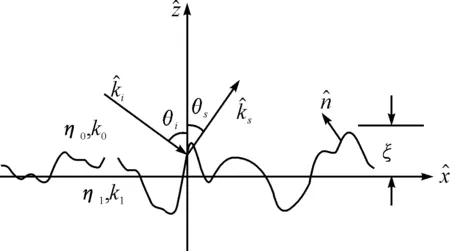
图1　激光在波动水面漫反射的几何关系

(1)

那么，根据Stratton-Chu公式[3]，结合由麦克斯韦尔方程推导得到散射场的电场和磁场的积分方程和边界条件[4]，通过对粗糙海面散射场切向和法向进行分析，可以得出以下方程：

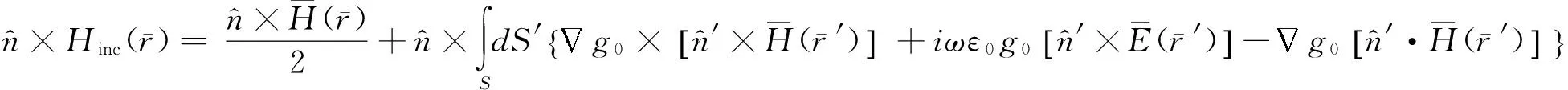
(2a)

(2b)

(2c)

(2d)

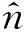
(3)

(4)

(5)

3矩阵离散

将光斑在x-y平面上的投影区域Sxy均匀划分成Nx×Ny个网格，该区域的每个采样点位于每个网格的中心处。在x和y方向上，每个网格的边长分别为Δlx=Lx/Nx和Δly=Ly/Ny。令m，n分别代表该点在网格中的横向和竖向序号，则该区域上的积分顺序如图2所示。

从图2中可以看出，采样点的排序是按照从下到上，再从左到右的顺序。其中，rd的定义将在下节进行介绍。

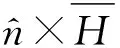
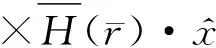
(6a)

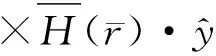
(6b)

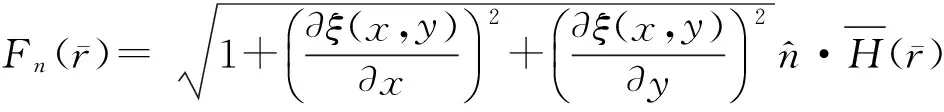
(6c)

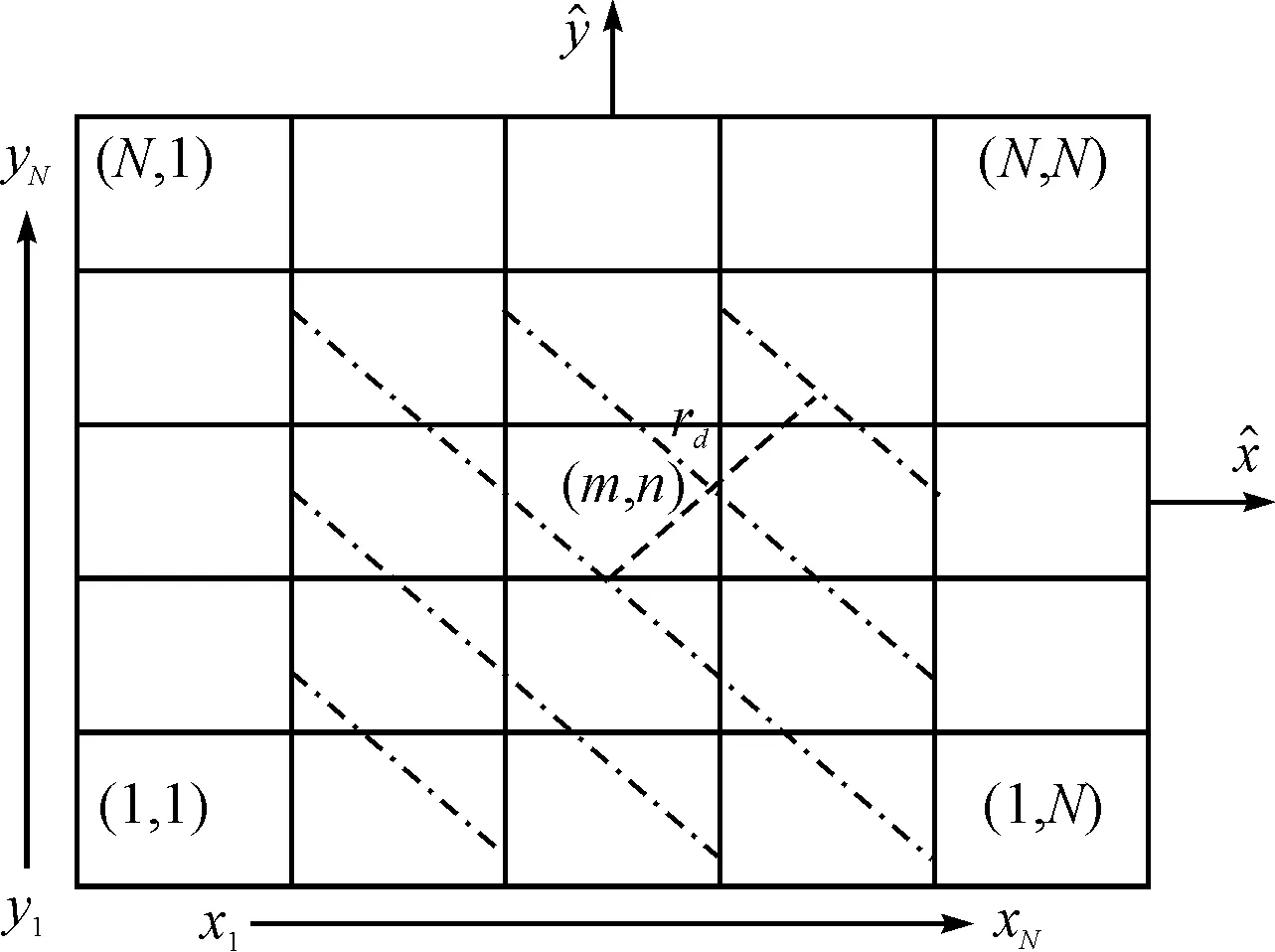
图2　Sxy的离散示意图

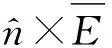
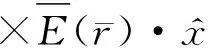
(7a)

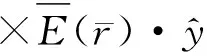
(7b)

(7c)

经过矢量分解后，根据式(2)可以得到以下六个关于标量场的方程。为了便于数值计算，根据矩量法(Method of Moment, MOM)对这六个标量方程进行离散，离散后的矩阵方程表示为

(8)

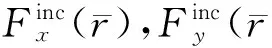
4稀疏矩阵规则网格法(SMCG)

由于源点和接收点的水平距离越近，源点对接收点的贡献就越大，因此，离接收点近的区域为强区，反之为弱区。SMCG[6]是一种效率很高的数值计算方法，它对强区源点的贡献进行详细计算，而对弱区源点的贡献则采取近似计算，在保证准确度的同时，极大地节约了计算成本。

为了便于说明，假设存在如下方程：

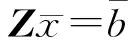
(9)

按照上述的强弱区域划分原则，可以将式(9)中的系数矩阵分解为如下形式：

Z=Z(s)+Z(w)

(10)

用稀疏矩阵来表示强区矩阵Z(s)，对于弱区矩阵Z(w)的元素，将其中的格林函数用泰勒级数展开求和的方式来近似表示，即：

(11)

(12)

其中，am，bm分别代表利用泰勒级数对G(R)和g(R)进行展开时的第m级系数，下标或上标中的0代表大气中的相应参数，1代表水中的相应参数。

在数值计算中，为了达到理想的精度，将泰勒级数展开至第6项，即M=5。根据泰勒级数的展开式，可以将弱区矩阵Z(w)表示为级数求和的形式，即：

(13)

令式(13)中的第1项为x-y平面的贡献Z(FS)，即：

(14)

则SMCG的迭代过程可以简单表述如下：

(15a)

(15b)

(15c)

第n次迭代过程结束后的相对误差Er定义为

(16)

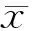
在具体的求解过程中，采用共轭梯度法(Conjugate Gradient Method, CGM)[7]来进行计算。由于Z(FS)是一个满矩阵，因此CGM在每步的迭代过程中，要消耗巨大的计算量来计算它与向量的乘积。通过Z(FS)的表达式发现，ZFS是一个分块托普利兹矩阵。它与向量的乘积满足卷积运算，因而可以用FFT来实现。令T为Z(FS)的一个分块矩阵，T的第1列为T1，则具体的计算方法为：

Tx=T1⊗x=ifft(fft(T1)·fft(x))

(17)

其中，⊗表示卷积运算符，fft表示快速傅里叶变换，ifft表示快速傅里叶反变换。

5锥形入射波

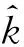
(18)

(19)

(20)

(21)

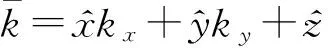
(22)

t=tx+ty

(23)

(24)

(25)

(26)

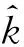
入射激光束的总能量为

(27)

6数值计算与分析

假设波动水面是一种分布式的随机过程，则采用归一化微分散射截面，即散射系数来表征粗糙面角度性的散射特征。三维激光漫反射在不同偏振状态下的双站散射系数可以被定义为[9]

(28)

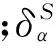
通过对双站散射系数进行立体角的积分求和，可以得到不同偏振状态的入射激光以角度θi入射时所产生的散射场的总能量与入射能量的比值Prβ(θi)，具体的表达式为

(29)

本文采用基于高斯谱的高斯随机过程[10]来模拟二维随机粗糙海面。为了模拟粗糙海面不同的粗糙度，建立了A、B两种海面模型来模拟不同粗糙度的波动水面。其中模型A的均方高度hx=hy=0.5cm，相关长度lx=ly=6cm;模型B的均方高度hx=hy=1cm，相关长度lx=ly=5cm。

为了说明三维激光海面漫反射的能量分布特性，以水平偏振为例，仿真计算了三维激光海面漫反射的双站散射系数，即γ=γhh。在仿真计算实例中，分别取入射角θi1=20°和θi2=60°，入射方位角φi1=φi2=0°。由于激光的能量相当集中，为了保证仿真结果的准确性，将计算了光斑的全部面积，参与散射的粗糙面的面积取为光斑面积的16倍，则相应的锥形波照射区域参数和粗糙水面的参数分别为gx1=gy1=0.01cm，Lx1=Ly1=0.04cm和gx2=0.02cm，gy2=0.04cm，Lx2=0.08cm，Ly2=0.16cm。激光波长为λ=0.532μm，为了保证激光的电磁特性，在x和y方向上的采样间隔为Δlx=Δly=λ/10。

采用SMCG进行数值计算，当取入射角θi1=20°时，用来区分强弱区域的临界距离rd1=40λ，当取入射角θi2=60°时，用来区分强弱区域的临界距离rd2=100λ。为了得到散射场能量分布的统计特性，采用蒙特卡洛方法进行仿真，蒙特卡洛仿真次数为500次。具体的三维激光海面漫反射双站散射系数的仿真结果如图3和图4所示。

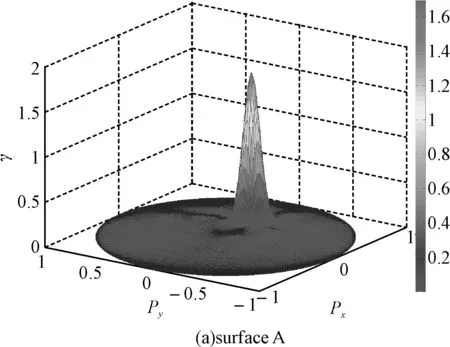
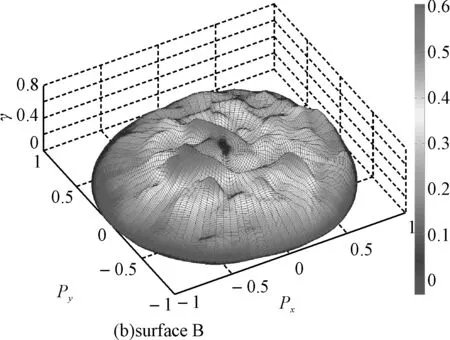
图3　当入射角θi1=20°入射不同粗糙度的界面时的双站散射系数

由于Matlab中没有直接绘制属于三维极坐标系下数据图形的命令，如果直接采用散射角θs和散射方位角φs作为直角坐标系的变量的话，当散射方位角θs相同时，φs=0°和φs=360°的双站散射系数是无法重合的。因此，为了形象、直观地描述散射场三维能量分布的角度特性，将散射角θs和散射方位角φs转换为直角坐标系下的坐标值Px=sinθscosφs，Py=sinθssinφs。

从图3和图4中不难看出，当界面的粗糙度相对较小时，散射场的能量分布相对集中，镜面反射方向的峰值能量相对较大，邻近区域的能量相对较小;当界面的粗糙度适度增加时，镜面反射方向的峰值能量减少，邻近区域的能量有所增长，散射场的能量分布更加均匀，即散射场能量的覆盖范围变得更大。但是在散射场的边缘处，能量衰减速度仍然非常快。

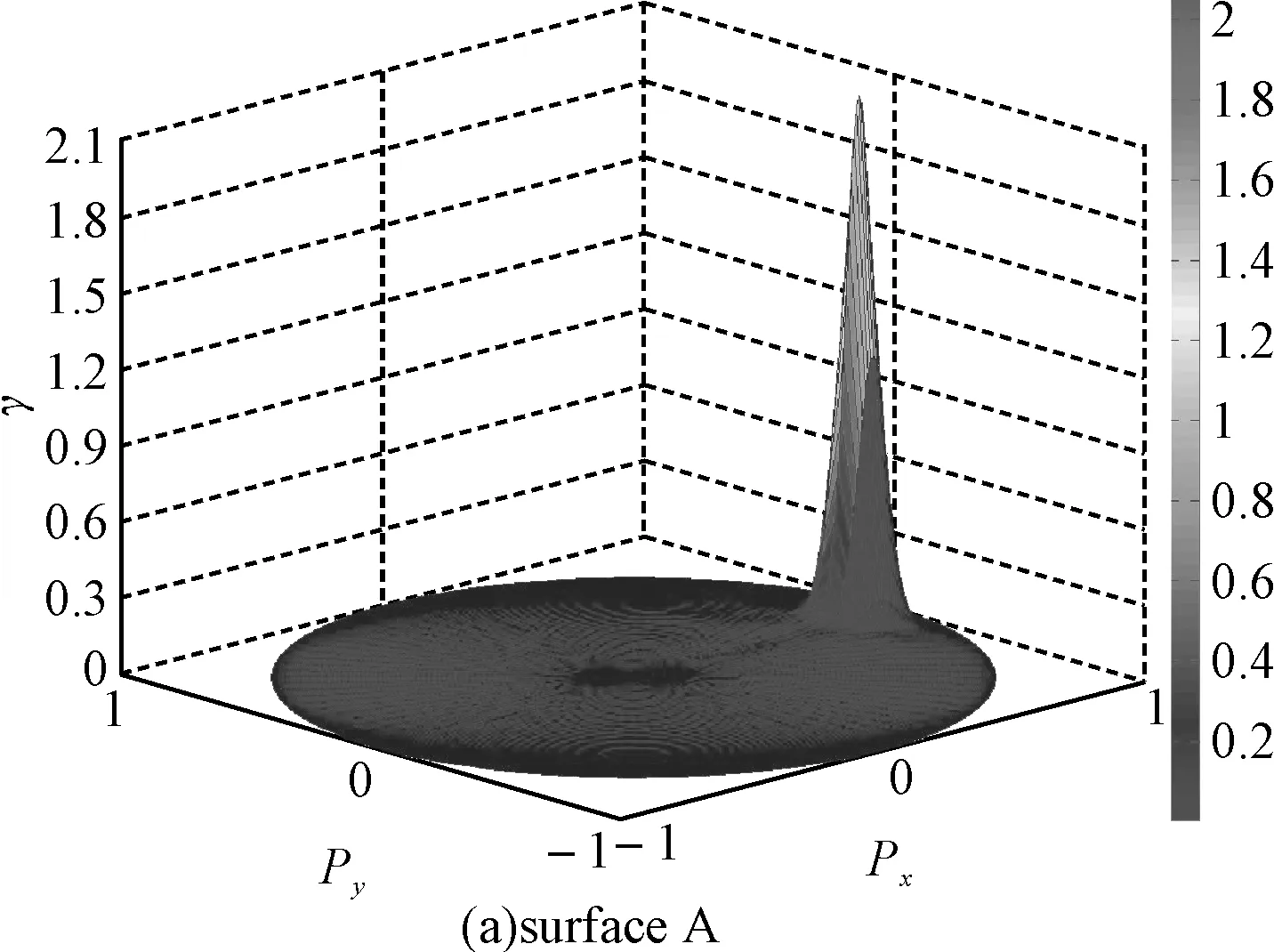
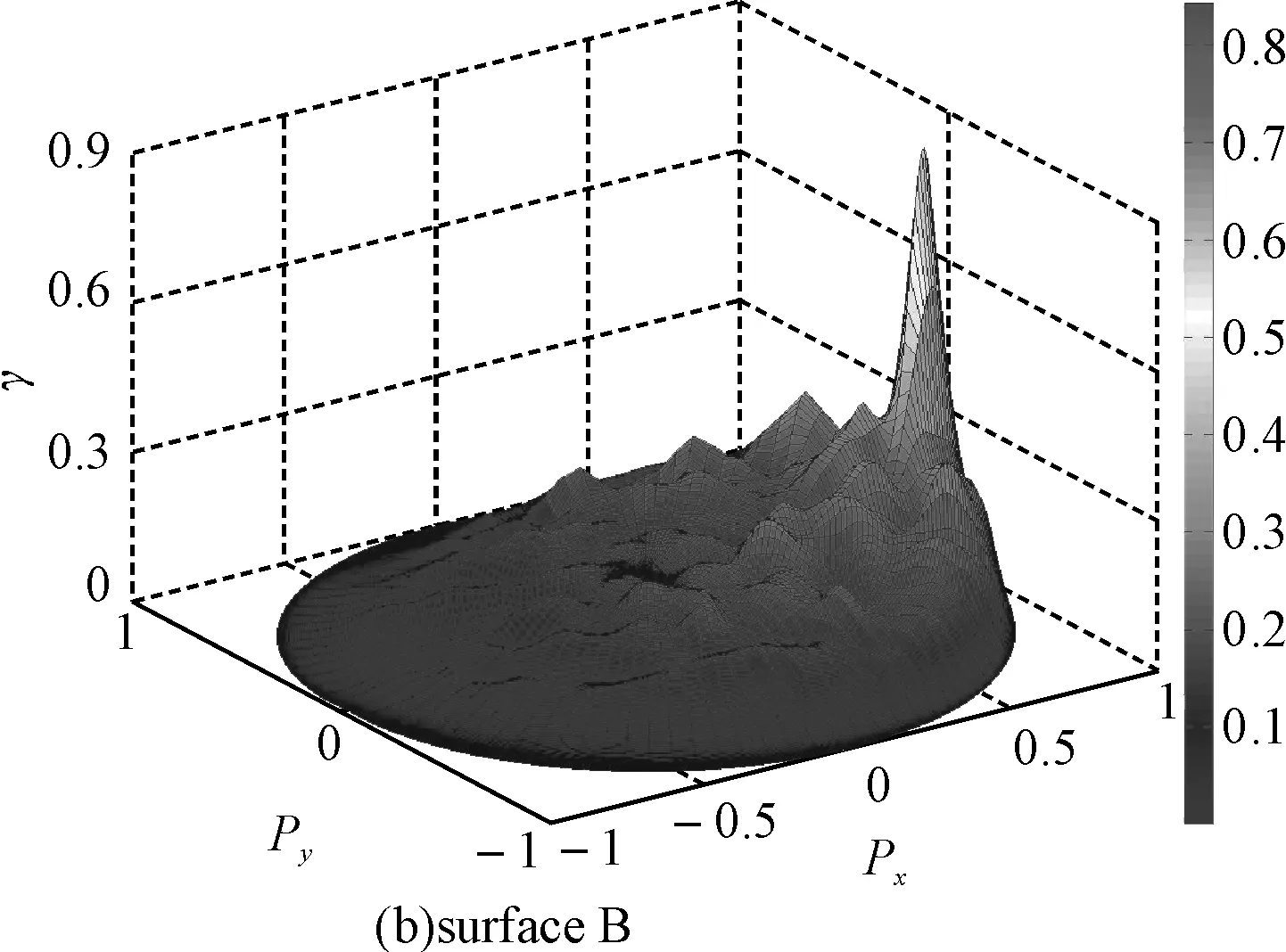
图4　当入射角θi2=60°入射不同粗糙度的界面时的双站散射系数

随着入射角度的增大，在粗糙面上的光斑面积和粗糙面的截断区域面积都会随之增加，因此就同一粗糙面而言，入射角度不同，粗糙面对激光的漫反射程度也不同，散射场的能量分布也存在这较大差别。通过图3(b)和图4(b)的对比可以看出，当入射角度θi1=20°时，散射场的能量分布相对于入射角度θi2=60°时的散射场的能量分布而言，峰值能量相对较弱，总体能量分布变得更加均匀。这就说明对于相同粗糙度的粗糙面模型，入射角度越小，粗糙面对激光的漫反射程度就会越大，散射场的能量分布就会越均匀。

7实验验证与分析

为了对三维激光海面漫反射双站散射系数的数值计算结果进行验证，在实验室中进行了实验。在实验室中，分别取入射角θi1=20°和θi2=60°，入射方位角φi1=φi2=0°，入射高度H=0.1m，采用功率为P=100mW，激光光束的发散角a=1mrad，波长λ=0.532μm的绿光水平偏振连续激光器。为了获得较为准确的实验数据，利用造波器生成两种不同粗糙度的波动水面，其中波动水面A的均方高度hx=hy=0.5cm，相关长度lx=ly=6cm;波动水面B的均方高度hx=hy=1cm，相关长度lx=ly=5cm。利用147型激光功率计对散射场中不同方位的采样点的能量进行多次测量，测量结果经过处理后，再与仿真计算结果进行对比。

实验中，对激光在入射角度θi2=60°，入射高度H=0.1m的情况下入射在不同粗糙度的波动水面上时，将散射场的能量变化呈现在另一端的背景墙上，并对散射场的漫反射能量分布情况进行了拍摄，具体的拍摄结果如图5所示。

图5　不同粗糙度的水面产生的散射场

通过图5(a)与图5(b)的对比，可以观察到图5(b)中背景墙上的光斑面积明显增大，整个光斑的亮度分布仍然前向镜面反射方向附近的亮度最高，越靠近边缘，亮度越低。但是，相对于图5(a)而言，光斑中心的亮度明显降低，而且在边缘处的能量衰减速度也相对较慢。这说明粗糙度较大的水面使得散射场的能量分布更加均匀，散射场的覆盖面积明显增大。

以上通过直接观察得到的激光漫反射能量分布特性，与对仿真结果进行分析后得出的激光漫反射能量分布特性是一致的。接下来，为了获得更加客观、量化的激光漫反射能量分布特性，将利用通过多次实验测得的数据，对三种不同方法(KA、2DFBM和3DSMCG)得出的散射场能量分布特性进行验证、对比和分析。

为了更加清楚地表示散射场能量在前后向上的分布，令散射方位角φs=0°时的散射角为正，即为前向。φs=180°时的散射角为负，即为后向，则采用的三种不同方法所得出的漫反射率以及实验数据之间的对比结果如图6、图7所示。

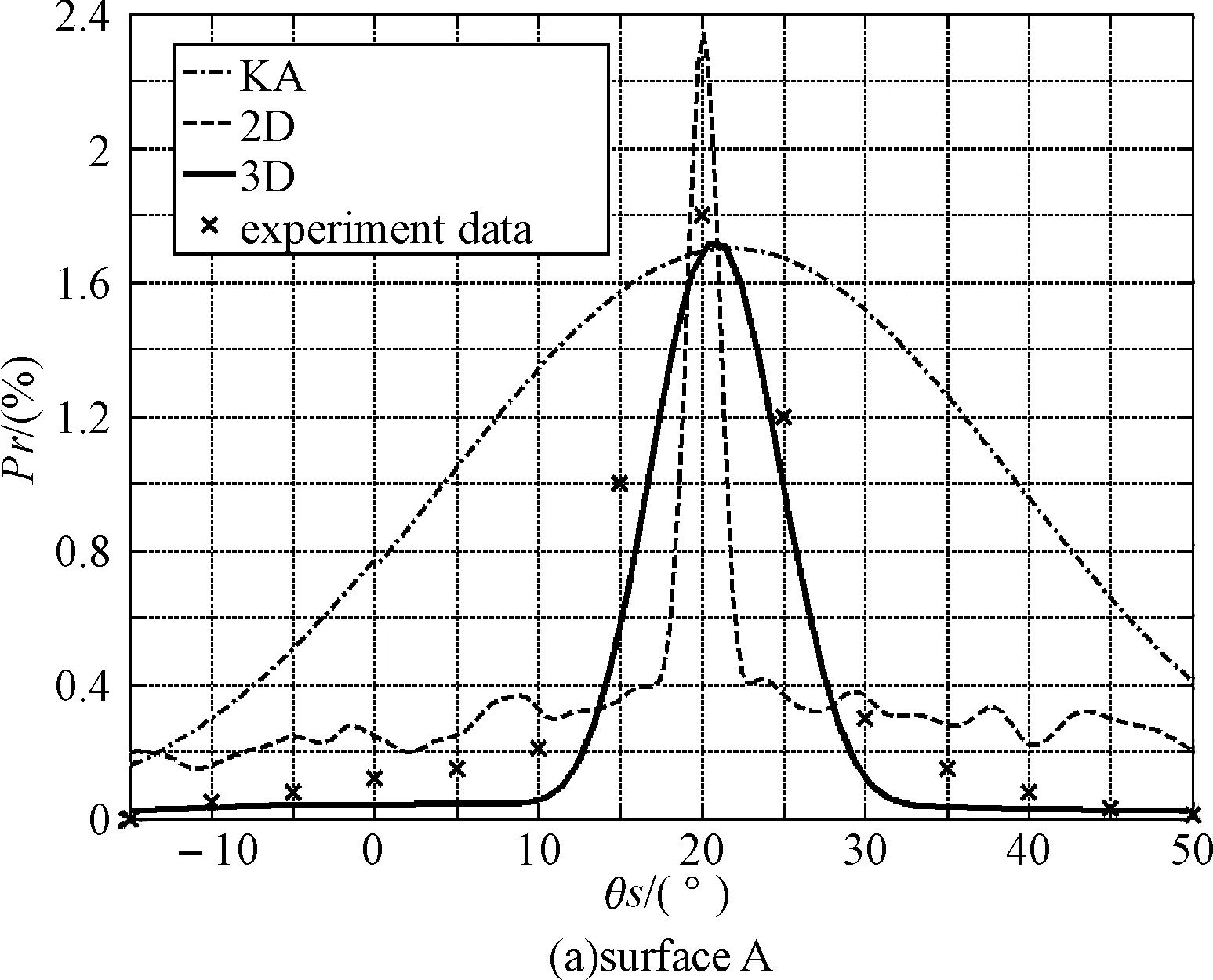
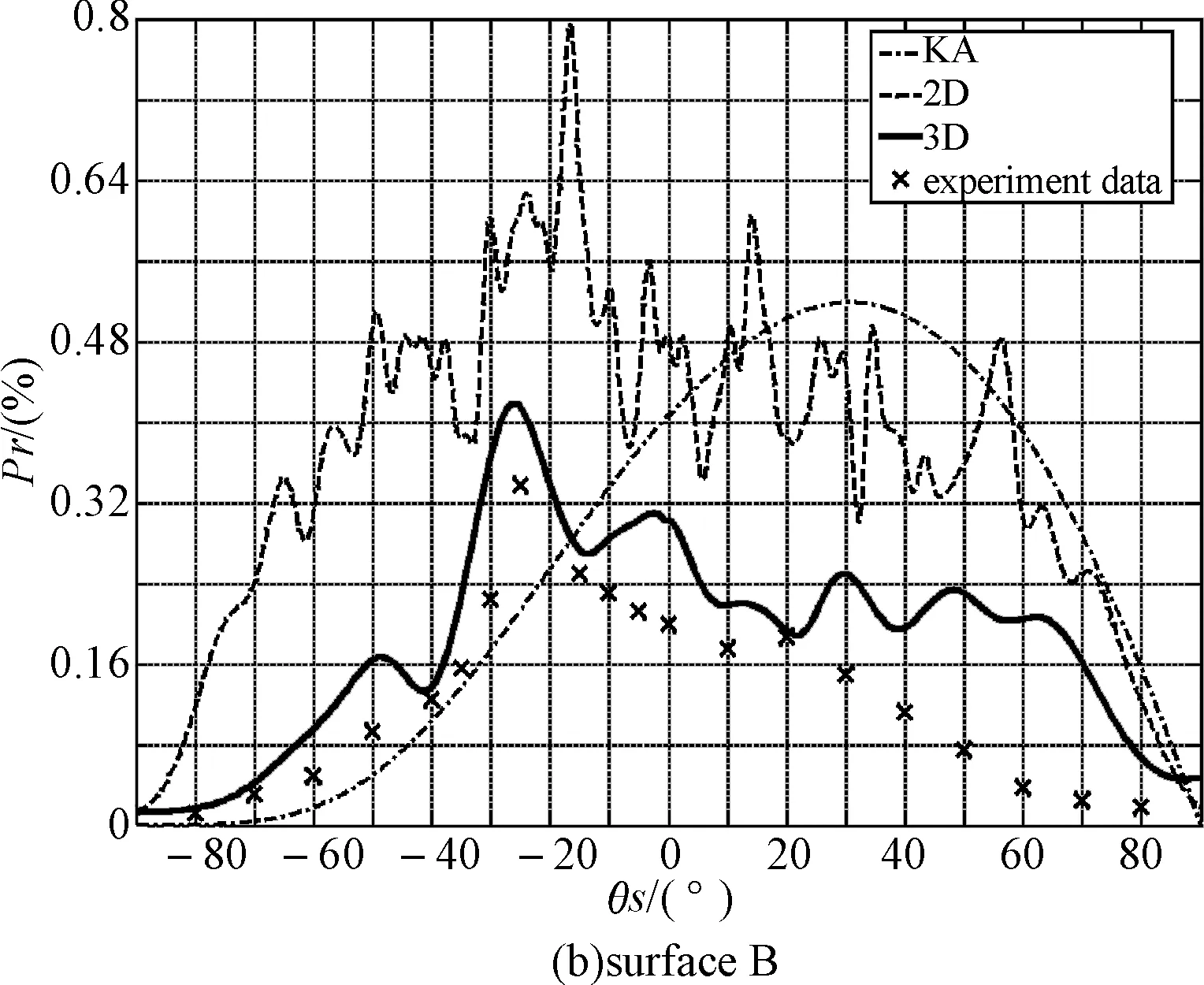
图6　θi=20°时的漫反射率

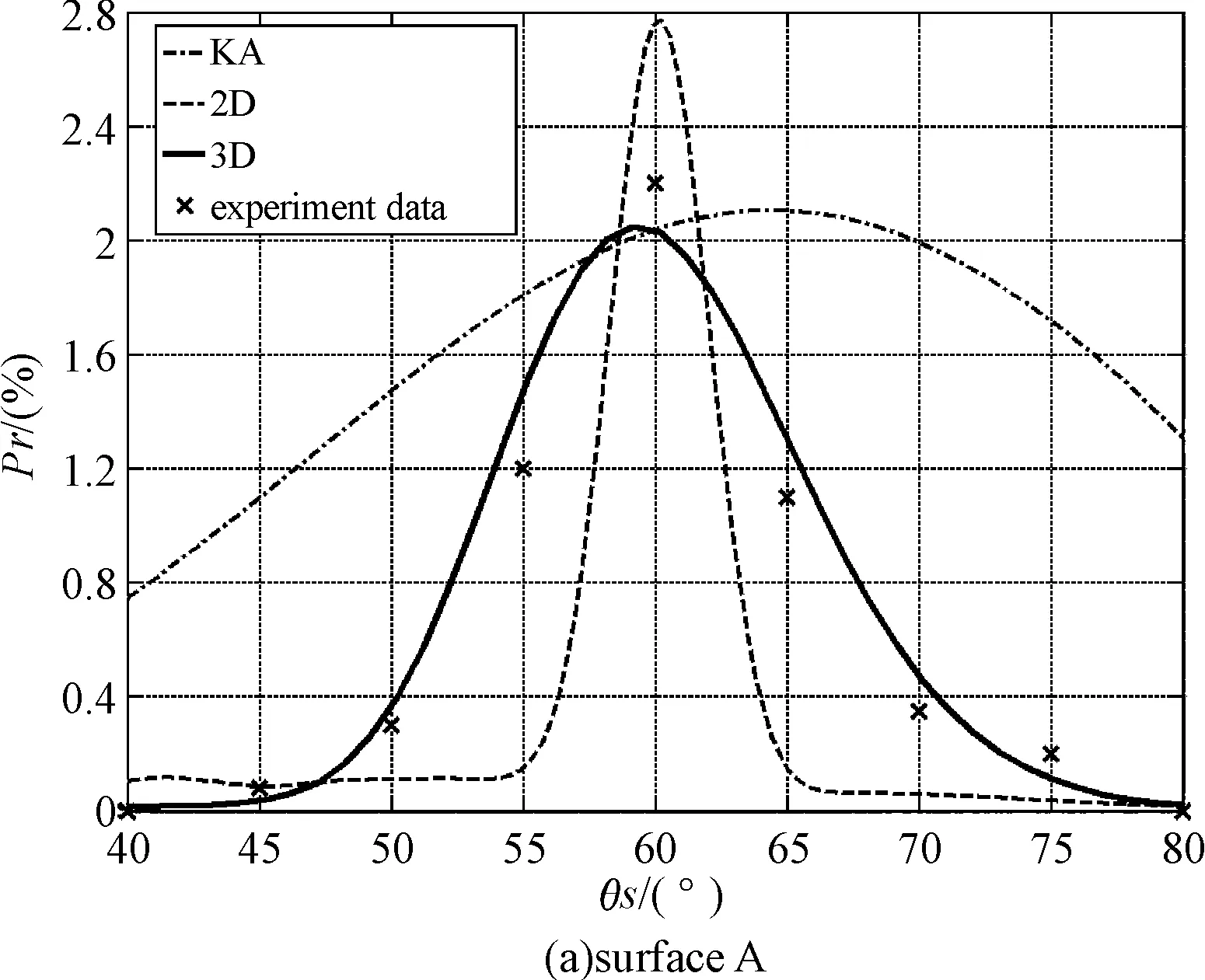
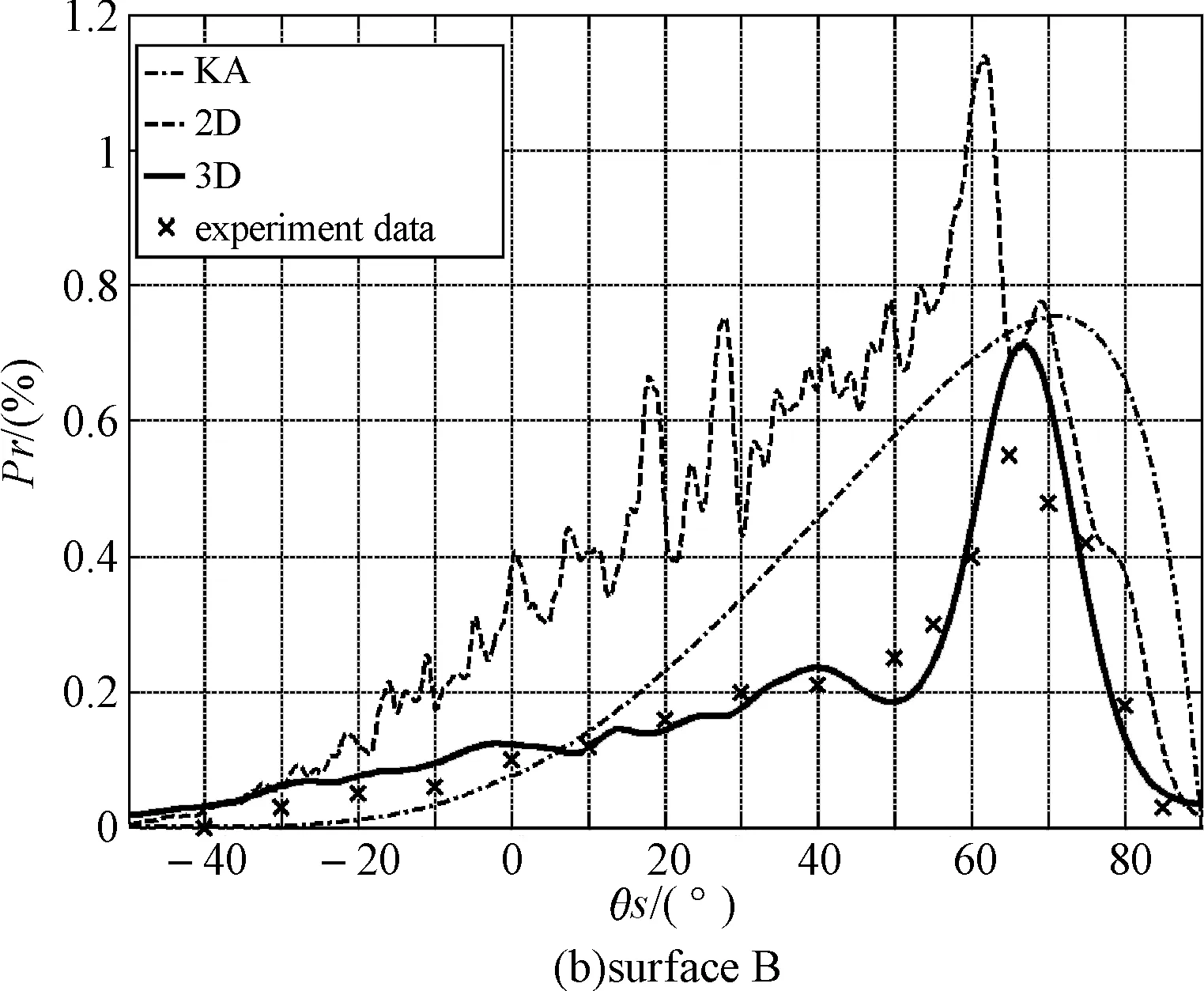
图7　θi=60°时的漫反射率

通过图6和图7中二维和三维仿真结果与实验数据的比对，发现通过三维数值计算仿真得出的漫反射率与实验数据更为接近。由于KA是一种解析算法，只能大致地估算散射场的能量分布特性，因此它是三种方法中最不准确的一个，甚至在图6(b)中，并未体现出散射场的后向增强现象。而二维数值计算的仿真结果相对于实验数据要大一些。从理论上分析，这主要是因为二维数值计算的仿真结果所代表的能量之和就是粗糙面上所有源点产生的贡献之和，即二维散射场的总能量。而三维数值计算的仿真结果与真实情况更为接近，图5和图6中代表三维漫反射率的曲线所代表的能量之和只是粗糙面上所有源点产生的贡献的一部分，并不是三维散射场的总能量。虽然三种计算方法在准确度上存在差异，但是所反映出来的散射场的能量分布特性上来讲还是相近的。

关于实验数据与三维双站散射系数之间存在的偏差，经过认真分析之后，认为主要是由于以下原因造成的：

1) 实验条件的客观因素，不可避免的会出现一些误差;

2) 粗糙海面的理论模型和真实水面还有一定差距。

8结语

本文采用数值计算方法对激光在波动水面上的三维漫反射特性进行了研究和实验验证。并且通过与其他方法得出的计算结果进行对比之后，认为三维数值计算方法得出的三维BSC是最能准确反映散射场能量分布特性的。通过分析研究，发现散射场的能量分布与入射角度和水面的粗糙度有着密切的关系，区分散射场能量前后向分布大小的入射角度随着粗糙度的变化而变化，粗糙度越大，入射角的分界点就越大。并且较为粗糙的水面会使得散射场的能量分布更加均匀，在散射场的边缘

处能量迅速衰减。

参 考 文 献

[1] 刘春香,程传福,任晓荣,等.随机表面散射光场的格林函数法与基尔霍夫近似的比较[J].物理学报,2004,53(2):427-435.

[2] 梁华锋,赖建军,彭中良,等.用于气体传感的一维光子晶体窄带红外发射光源[J].红外与毫米波学报,2009,28(6):414-417.

[3] 杨雨川,谭吉春,盛定仪,等.导体板上单极天线对电磁脉冲响应特性的矩量法分析[J].强激光与粒子束,2008,20(4):649-652.

[4] 崔志伟,韩平,李明磊.磁化等离子覆盖导体散射问题的FE/BI方法分析[J].电波科学学报,2010(5):973-978.

[5] 吴国荣,钟伟芳,吴永东.半空间弹性波强散射双参数非线性反演[J].华中科技大学(自然科学版),2003,31(4):105-107.

[6] H T Chou and J T Johnson. A novel acceleration algorithm for the computation of scattering from rough surfaces with the forward-backward method[J]. Radio Sci.,1998,33(4):1277-1287.

[7] Tsang L, Kong J A. Scattering of Electromagnetic Waves-Numerical Simulation[M]. New York: John Wiley,2001：201-203.

[8] 叶红霞,金亚秋.随机粗糙面上介质目标差场散射的快速计算方法[J].电子学报,2006,34(6):1074-1079.

[9] Tsang L, Kong J A. Scattering of Electromagnetic Waves-Numerical Simulation[M]. New York: John Wiley,2001：56-60.

[10] Lei Kuang, Yaqiu Jin. Bistatic Scattering From a Three-Dimensional Object Over a Randomly Rough Surface Using the FDTD Algorithm[J]. Antennas and Propagation, IEEE Transactions on,2007,55(8):2302-2312.

收稿日期：2016年1月14日,修回日期：2016年3月2日

作者简介：姚瑶，女，博士，工程师，研究方向：水下目标探测。

中图分类号TN219

DOI：10.3969/j.issn.1672-9730.2016.07.037

Characteristics of Laser Scattering from Rough Water Surface Based on Detection of Underwater Stealth Moving Target

YAO YaoSUN XiaofengTAO Yongqin

(No.702 Factory of Navy, Shanghai200434)

AbstractTo enhance the detection efficiency of satellite against underwater stealth moving targets, the characteristics of the scattered field of laser from the water surface in different roughness and incident angles was studied. First, the coupling relationships among components in different directions were analyzed and the corresponding matrix equations from Maxwell equations and boundary conditions were solved with SMCG. Second, the 3D model of incident laser beam was established with 3D tapered wave. Finally, the 3D BSC was get and verified by experiments. The results showed that the 3D BSC was enough accurate to express the characteristics of laser diffusion from water surface so that some contributions were made for the further study about the characteristics of laser diffusion from sea surface.

Key Wordslaser, submarine, UUV, diffusion, bistatic scattering coefficient, sea surface