可靠性维修性与LCC的关系模型研究*

曹　凯　黄　政　陈砚桥　刘晓威

(1.海军工程大学动力工程学院　武汉　430033)(2.海军工程大学舰船动力工程重点实验室　武汉　430033)



可靠性维修性与LCC的关系模型研究*

曹凯1,2黄政1,2陈砚桥1,2刘晓威1,2

(1.海军工程大学动力工程学院武汉430033)(2.海军工程大学舰船动力工程重点实验室武汉430033)

摘要论文针对装备可靠性、维修性与寿命周期费用关系模型开展研究。该文分析了寿命周期费用影响因素，构建了寿命周期费用分解结构;在此基础上，建立了论证研制费和购置费和维修费与可靠性维修性关系模型，并综合形成寿命周期费与可靠性维修性关系模型。通过案例分析，由统计数据确定了模型中待定参数，通过权衡分析，给出了寿命周期费最少的可靠性维修性指标，验证了所建立的模型的正确性。所建立模型对综合权衡确定最佳可靠性维修性指标具有一定理论价值及现实指导意义。

关键词寿命周期费用; 可靠性; 维修性

Class NumberTN219

1引言

据外军统计，第三代战机F/A-18比第二代战机F-4J可靠性提升三倍，维修性提升两倍，由此，在20年寿命周期内可节约保障费用600多万美元[1]。提高装备的可靠性维修性，可以延长平均故障间隔时间(MTBF)，缩短平均修复时间(MTTR)，减少故障数量和维修时间，从而大幅缩减保障费用。但这对制造工艺、材料选择、工程设计、装配精度要求更高，会造成研制生产费用大幅增加。因此，为了降低寿命周期费用LCC，需要对可靠性维修性权衡分析，以较小的研制生产费用增幅获得较大的使用保障费用降幅，使得寿命周期费用显著减少。

目前，寿命周期费用分析技术已经在民用和军事领域广泛运用[2～5]。可靠性维修性的权衡分析需要明晰可靠性维修性与LCC的关系，国内外学者针对寿命周期费用与可靠性维修性关系模型开展了大量研究。文献[6]根据费用分解结构原理，给出了寿命周期费用分解图，建立了装备寿命周期费用优化模型。文献[7]在美国著名质量管理专家朱兰博士(Dr.JM Juran)提出的质量成本模型的基础上，建立了可靠性和寿命周期费用的数学模型。文献[8]提出了基于可靠度和MTBF的费用估算模型。文献[9]考虑安全性因素，将故障后果费用引入维修保障费用，提出了基于可靠性和维修性的寿命周期费用估算模型，并给出了仿真模型。

由上述文献可知，国内外学者针对可靠性、维修性对寿命周期费用影响问题的研究较深入，取得很多成果，但是大多分别考虑可靠性、维修性与寿命周期费用的关系，没有综合分析两者共同作用的影响。现有模型特别是维修费估算模型没有详细分析装备工作和维修过程，精度有所欠缺。

针对上述问题，本文将分析装备寿命周期费用影响因素，并进行费用分解;建立可靠性维修性与研制购置费、维修费关系模型;综合形成可靠性维修性与寿命周期费关系模型。并通过案例分析，由统计数据确定模型中待定参数，通过权衡分析，给出寿命周期费最少的可靠性维修性指标，验证所建立的模型的正确性。

2寿命周期费用的分解

寿命周期费用(Life Cycle Cost, LCC)指装备在预期寿命周期内，为论证、研制、生产、使用保障以及退役处置所支付的所有费用总和[10]。为了方便估算，按照装备寿命周期时间顺序，将LCC分解为论证研制费CRD、购置费CP、使用与保障费COS和退役处置费CDR四大类。

2.1论证研制费和购置费

论证研制费CRD和购置费CP影响因素众多，很难用数学推导的方式建立可靠性维修性与各项费用的定量关系。不妨通过综合分析论证研制费和购置费与可靠性维修性的定性关系，确定公式的形式与特点，再通过数据分析的方法，完善和改进模型。

2.2使用与保障费

使用与保障费COS占寿命周期费用的比例超过60%，根据“冰山理论”[9]，如果把寿命周期费用比作一座冰山，那么购置费只相当于冰山漏出水面的部分，而使用与保障费相当于水面以下看不到的冰山主体。使用与保障费由使用费、维修费、改换装费和保障费组成。其中维修费与装备可靠性维修性关系密切，且在使用与保障费中占较大比例，因此本文将重点针对维修费开展研究。

根据文献[11]，维修费是装备使用期间为维修装备花费的所有费用总和，包括维修设备费、维修设施费、维修器材费、维修人员费和其他维修费。维修保障是一个复杂的系统工程，要求完善的保障系统作为支撑，需要大量的保障资源。根据各项费用对寿命周期费用的影响形式，可以将维修费分成三类，前期投入型费用、随时间增长型费用、故障引入型费用。

前期投入型费用是根据装备系统保障性要求，在装备服役之初建立维修保障系统所产生的费用，属于一次性投入型费用，主要包括维修设施费、维修设备费以及维修人员培训费。根据装备系统研制阶段制定的维修保障方案可以求得这部分费用。随时间增长型费用是指随着装备维修时间的增长逐渐提高的费用，这部分费用与维修时间成正比，这里主要包括维修人员工资费。故障引入型费用是指每次用于维修故障元件投入的维修器材费用。

除了维修费，使用与保障费中的其他费用项目与可靠性维修性并没有显著关系，所以将其设为定值CI。

2.3退役处置费

退役处置费CDR在寿命周期费用中所占的比例较小，且与可靠性维修性没有显著关系，本文忽略这部分费用。

3论证研制费和购置费与可靠性维修性关系模型

可靠性维修性对装备研制购置费的影响形式十分复杂，直接用解析法推导关系式非常困难。本节通过分析可靠性维修性与各项费用的关系，明确模型形式和特点，根据实际研究背景，论证模型是否合理。然后，应用回归分析方法，改进和完善模型。

可靠性是表征装备质量的重要参数，为了达到较高的可靠性水平，在研制设计阶段需要开展可靠性设计，进行可靠性试验，采用冗余设计，并在生产制造阶段要采用更好的材料更先进的工艺，因此相对于不开展专门可靠性设计，要投入更多经费。在可靠性水平较低阶段，投入较少经费即可获得较大可靠性水平提升;在可靠性水平较高阶段，投入大量经费却只能获得较少可靠性提高。若以平均故障间隔时间MTBF为可靠性指标，论证研制费和购置费随着MTBF的提升先缓慢增加，随后加速增长。

维修性是表征装备质量的另一个重要参数，主要取决于研制设计和生产制造，关键在于研制设计。研制阶段的维修性工作主要有维修性建模、维修性分配、维修性预计和维修性分析等内容。维修性较低阶段，投入较少的研制经费就可以获得较高的维修性水平提高;在维修性较高阶段，投入大量研制费却只能获得较少维修性提高。若以平均修复时间MTTR为维修性指标，论证研制费和购置费随着MTTR的减小先缓慢增加，随后加速增长。

如果可靠性与维修性相关工作单独开展，互不影响，在文献[7，13]所建模型的基础上，可给出论证研制费和购置费与可靠性维修性的关系模型：

(1)

式中：λj为第j个单元的故障率，Ru为现有技术水平和条件下能达到的可靠度上限，Kj为待定系数，可利用最小二乘法结合统计数据确定。

由上述分析可知，当可靠度趋近于可靠度上限时，论证研制费和购置费趋近于无穷;当平均修复时间趋近于零时，论证研制费和购置费也趋近与无穷，该模型可以描述论证研制费和购置费随可靠性维修性变化的趋势。

4维修费与可靠性维修性关系模型

维修费受多种因素影响，传统的解析法对实际情况通常简化过度，计算误差较大。本文将寿命周期划分为m个相等的微单元，借助仿真思想，模拟元件寿命周期过程，建立元件维修状态矩阵和故障状态矩阵，进而给出维修费与可靠性和维修性的关系模型。

把元件的寿命周期T分解为m个长度为Δt的微单元，按照前文维修费的三种分类，该元件在第i个微单元的维修费可以表示为

CM i=Cβ i+Cγi

(2)

式中：CM i为元件在第i个微单元内的维修费;Cβ i为元件在第i个微单元内的维修人员工资费;Cγ i为元件在第i个微单元每次故障引入维修器材费。

装备维修费可表示为

(3)

式中：CM为装备的维修费，Cα为前期投入费用。

设寿命周期T的第i个微单元的故障概率为hi，维修概率为pi，则式(3)可表示为

(4)

式中：Cγ=Cγi为每次维修器材费(此处假设每次维修的维修器材费用相同)，Cβ为单位时间维修工资费。

为使模型更符合实际，做如下几点假设：

1) 系统由单元件组成，故障后维修，恢复完好;

2) 忽略保障延误时间对维修时间的影响;

临床术后诊断的肋骨骨折118处，其中背段、腋段、前段和软骨段分别为38、58、15和7处，诊断符合率分别为97.4%、96.7%、93.3%和71.4%。术后诊断不符合共6处，1处腋前交界区临床归为前段，1处腋后交界区临床归为背段，肋软骨线形骨折漏诊2处（表2）。

3) 忽略时间因素对维修费的影响;

4) 忽略预防性维修对维修费的影响。

元件故障间隔时间是与元件寿命分布函数密切相关的随机变量，其均值即MTBF。一次试验中元件在第i个微单元发生故障，修复后继续工作，在第i+n个微单元再次发生故障，再次修复，如此往复直到寿命T截止。如果把有故障发生的微单元记为“1”，其他单元记为“0”，就可以得到第一次试验的故障状态行矩阵α1×m。

元件维修时间是与元件维修时间分布函数密切相关的随机变量，其均值即MTTR。一次试验中元件在第i个微单元发生故障，在此单元后有若干个维修单元，具体维修单元个数由维修时间决定。如果把发生维修的微单元记为“1”，其他单元记为“0”，就可以得到第一次试验的维修状态行矩阵β1×m。

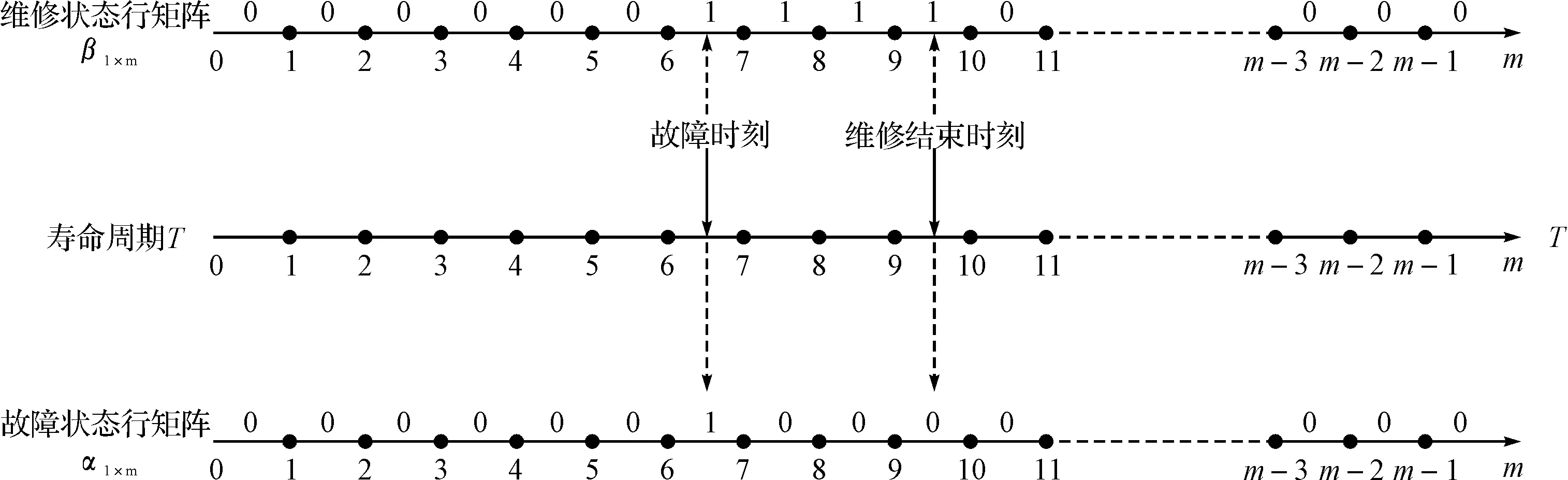
图1　维修状态行矩阵和故障状态行矩阵

重复上述过程N次，得到元件的故障状态矩阵AN×m和维修状态矩阵BN×m;

在故障状态矩阵AN×m中，统计落在第i列的故障数，用此次数除以N得到该单元元件故障概率hi(工程实际中通常把故障率定义为“产品工作到某一时刻，单位时间内发生失效的比例”);在维修状态矩阵BN×m中统计落在第i列的维修次数，用此次数除以N得到该单元元件维修概率pi;

由式(4)结合维修状态矩阵BN×m和故障状态矩阵AN×m可以推导出维修费与MTBF和MTTR的关系：

(5)

5寿命周期费用与可靠性维修性关系模型

在前面的分析中已经建立了论证研制费和购置费与可靠性维修性关系模型，维修费与可靠性维修性关系模型，结合装备寿命周期分解结构，可以建立寿命周期费用与可靠性维修性关系模型。

CT=CY+CM+CI

(6)

(7)

6案例分析

查阅技术资料得知某装备寿命服从指数分布，故障率为0.0018，使用可用度和战备完好率要求MTBF大于500小时，MTTR小于50小时，当前技术水平下平均故障间隔时间上限MTBFu为890小时，工作100小时的可靠度上限Ru为0.8937。于是，论证研制和购置费与可靠性维修性的关系可以表示为

(8)

参考相关资料，某装备论证研制费和购置费与MTBF和MTTR的经验数据如表1所示。

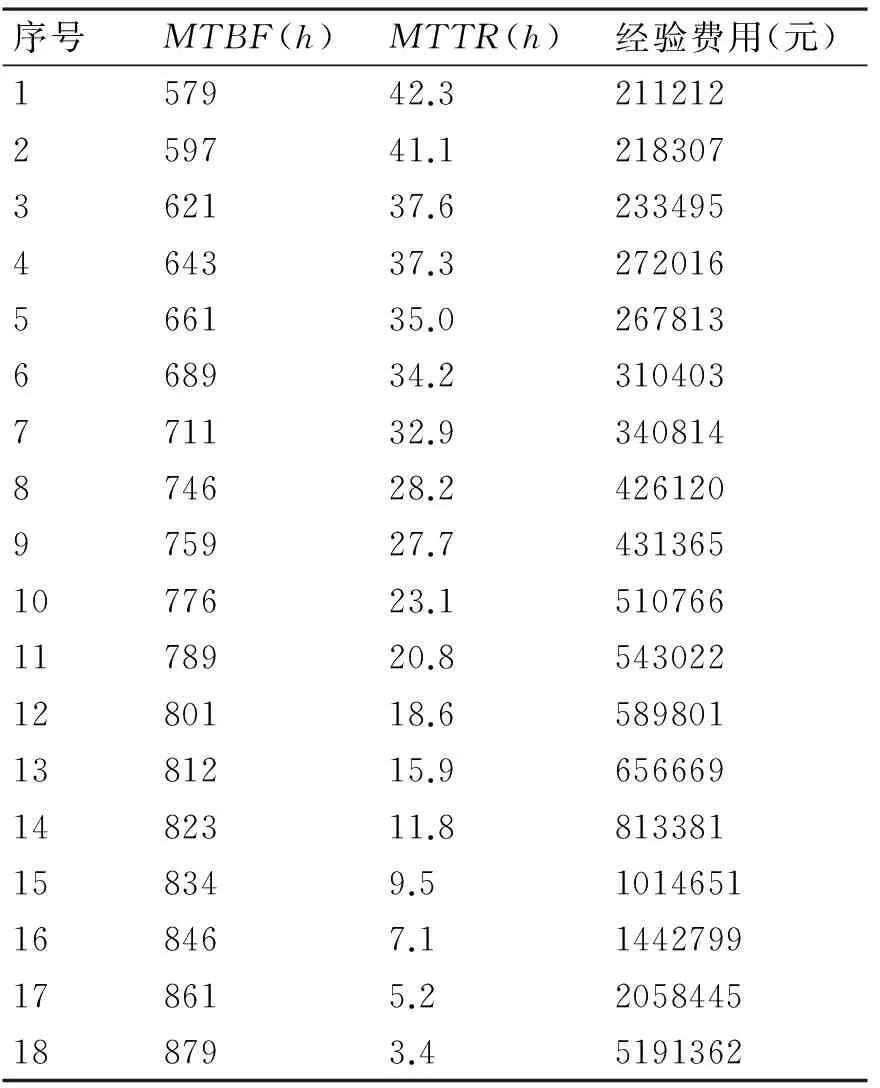
表1　论证研制费和购置费与MTBF、MTTR经验数据表

通过软件拟合出证研制费和购置费与MTBF和MTTR的关系为

(9)

(10)

通过数值计算，由式(10)可以给出MBTF和MTTR与论证研制费和购置费的关系，如图2所示。

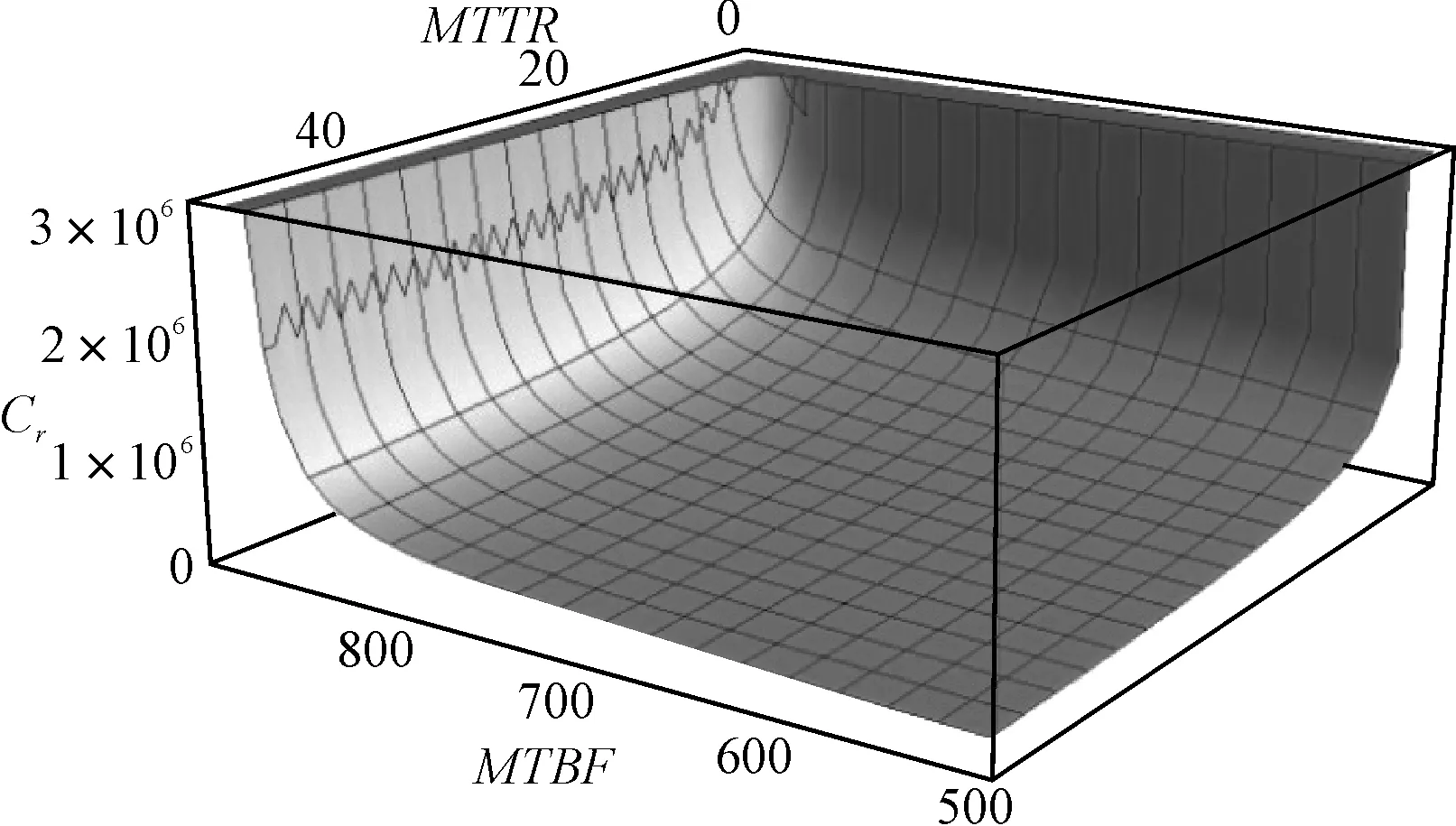
图2　MTBF和MTTR与论证研制费和购置费的关系

已知该装备寿命周期为10年，即87600小时，维修前期投入费用Cα为50000元，每次故障引入维修器材费Cγ为3000元，维修工资费Cβ为100元/小时，使用保障费中与可靠性维修性无关的费用CI为100000元，该装备寿命服从指数分布，故障率为常数，于是式(5)给出的维修费与可靠性维修性关系可表示为

(11)

通过数值计算，由式(11)可以给出MBTF和MTTR维修费的关系，如图3所示。

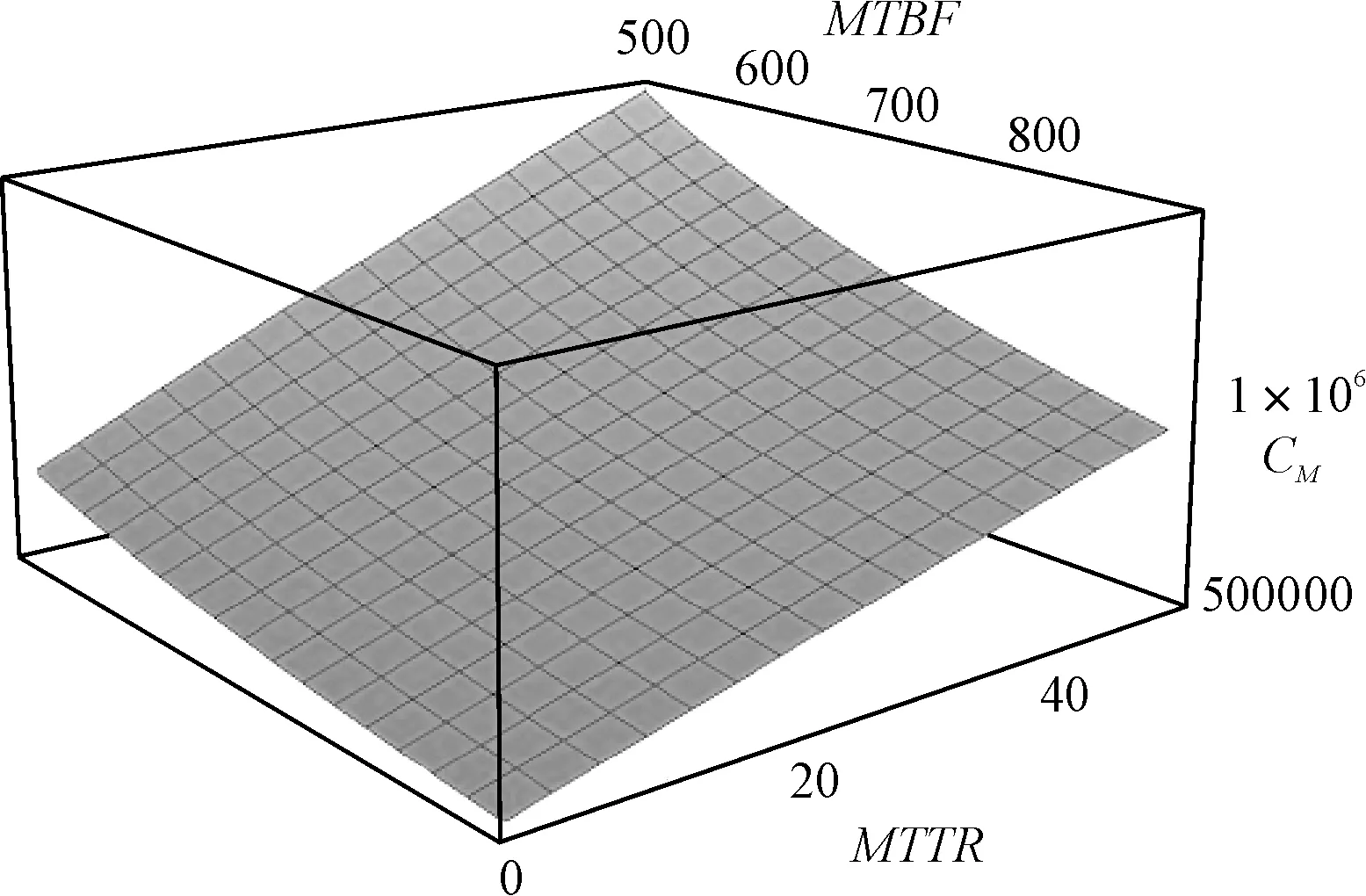
图3　维修费与MTTR和MTBF的关系

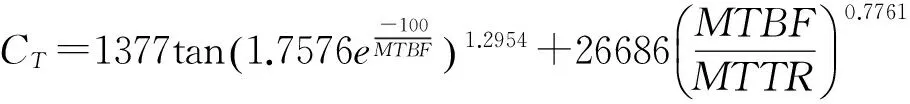
(12)

通过数值计算，由式(12)可以给出MBTF和MTTR维修费的关系，如图4所示。

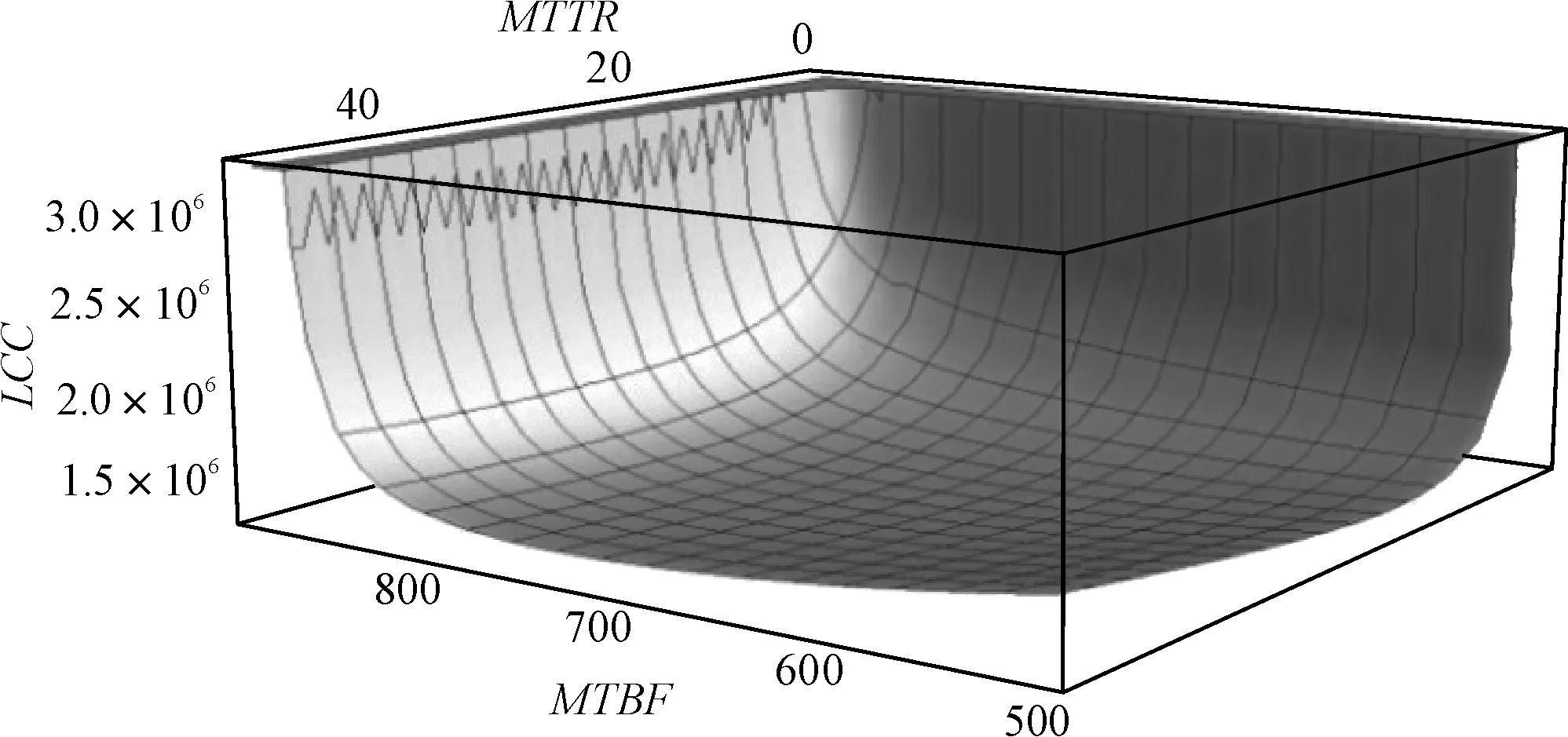
图4　寿命周期费用与MTTR和MTBF的关

由图4可知，寿命周期费用随着MTTR减小，先下降后加速上升，这因为随着MTTR的缩短，装备维修性提升，装备维修费随之减少，论证研制费和购置费增幅较小，寿命周期费用呈现下降趋势;随着MTTR的继续缩短，装备维修性继续提升，此时装备维修费小幅减少，但是论证研制购置费却大幅增长，甚至超过维修费的减幅，寿命周期费用呈现加速上升趋势。存在最佳MTTR，使得装备寿命周期费用最少。

寿命周期费用随着MTBF增大，先下降后加速上升，这因为随着平均故障间隔时间的延长，装备可靠性提升，装备故障数量减少维修费随之减少，论证研制购置费增幅较小，函数图像呈现下降趋势;随着平均故障间隔时间的继续延长，装备可靠性继续提升，此时装备维修费小幅减少，但是论证研制购置费却大幅增长，甚至超过维修费的减幅，寿命周期费用呈现加速上升趋势。存在最佳MTBF，使得装备寿命周期费用最少。

图4中，当MTBF为689小时，MTTR为24小时时，装备的全寿命周期费用最少为1240260元。通过前面建立的论证研制费和购置费、使用保障费模型，可以得出，此时的使用保障费为813450元，论证研制费和购置费为426809元，使用保障费占寿命周期费的比例为65.58%。

7结语

可靠性维修性是重要的质量参数，与论证研制购置费和使用保障费关系密切。本文分析了寿命周期费用影响因素，构建了寿命周期费用分解结构;在此基础上，建立了可靠性维修性与论证研制购置费和使用保障费的关系模型，综合形成了寿命周期费用与可靠性维修性关系模型;通过案例分析，由统计数据确定了模型中待定参数，通过权衡分析，给出了寿命周期费最少的可靠性维修性指标，验证了所建立的模型的正确性。建立的模型对估算各项费用、合理确定指标、优化参数匹配具有一定理论研究价值和现实指导意义。

参 考 文 献

[1] 束琬.面向飞机系统效能的机务维修效率研究[D].南京:南京航空航天大学,2012:16-17.

[2] 董芮寒,罗涛.装备可靠性与寿命周期费用相关关系模型研究[J].价值工程,2015(26):159-161.

[3] HE Weiyi, XU Xiaojie, GAO Xizhen, et al. Research on the Highway Engineering LCC Estimation Modular Platform[J]. Applied Mechanics and Materials,2014,3309(584):2554-2558.

[4] Gu-Taek Kim , Kyoon-Tai Kim , Du-Heon Lee , Choong-Hee Han , Hyun-Bae Kim,Jin-Taek Jun . Development of a life cycle cost estimate system for structures of light rail transit infrastructure[J]. Automation in Construction,2009,19(3):308-325.

[5] 罗水兰,王恩茂.节能住宅全寿命周期费用影响因素仿真研究[J].工程管理学报,2015(5):130-134.

[6] 刘鹏,董振旗,屈岩,等.武器装备系统寿命周期费用分析及优化模型[J].四川兵工学报,2012(5):57-59.

[7] 史秀建,金家善,吴奕亮.寿命周期费用与可靠性关系模型分析研究[J].武汉理工大学学报(交通科学与工程版),2004(4):589-592.

[8] 刘晓东,张恒喜.飞机可靠性与研制费用相关关系研究[J].空军工程大学学报,2000(1):63-66.

[9] 张作品.基于可靠性维修性系统的寿命周期费用分析[D].秦皇岛: 燕山大学,2010:1-2.

[10] 刘鹏,董振旗,屈岩,等.武器装备系统寿命周期费用分析及优化模型[J].四川兵工学报,2012,33(5):57-59.

[11] GJBz 20517-1998.武器装备寿命周期费用估算[S].中国人民解放军总装备部,1998:135-136.

[12] 李永杰,胡坚,汪厚祥.舰艇装备维修信息数据仓库的建立与数据挖掘[J].计算机与数字工程,2010,38(10):68-71.

[13] 蒋里强,王权伟,王桂花,等.武器系统维修性分配的规划方法研究[J].系统工程与电子技术,2007(1):155-157.

收稿日期：2016年1月17日,修回日期：2016年2月23日

作者简介：曹凯,男,硕士研究生,研究方向:可靠性维修性保障性工程。黄政,男,副教授,硕士生导师,研究方向:机械可靠性。陈砚桥,男,博士,讲师,研究方向:装备维修保障。刘晓威,男,博士,讲师,研究方向:现代热力学。

中图分类号TN219

DOI：10.3969/j.issn.1672-9730.2016.07.028

Life Cycle Cost Model of Reliability and Maintainability

CAO Kai1,2HUANG Zheng1,2CHEN Yanqiao1,2LIU Xiaowei1,2

(1.College of Power Engineering, Naval University of Engineering, Wuhan430033)(2.Military Key Laboratory for Naval Ship Power Engineering, Naval University of Engineering, Wuhan430033)

AbstractThis paper carried out a research of the relational model between the life cycle cost and reliability as well as maintainability. This paper constituted a decomposed structure of the life cycle cost by analyzing the influencing factors of the life cycle cost. Then it established relational models among purchase cost, development cost, maintenance cost and reliability as well as maintainability. Then it formed a relational model between the life cycle cost and reliability as well as maintainability by integration. It ensured the undetermined coefficient in the model through the related statistical data by means of case analysis, ascertained the best index for the least life cycle cost and confirmed the validity of the model. The model was valuable in ascertaining the best index and guidance for reality.

Key Wordslife cycle cost, reliability, maintainability