高阶数值流形方法的速度公式
2016-08-09苏海东
苏海东
高阶数值流形方法的速度公式
苏海东
(长江科学院材料与结构研究所,武汉430010)
高阶数值流形方法可以显著提高结构计算精度,但目前在涉及大位移的动力分析中往往得到精度很差、甚至不正确的速度结果。基于平面三角形数学网格和一阶多项式覆盖函数,通过一个刚体杆件旋转算例探讨其中的原因,得出必须考虑构形坐标变化对速度的影响,并提出高阶流形法的3种速度处理方法及相应的高阶速度公式。该方法对一些在结点处增加广义自由度的类似方法(如广义有限元)的几何非线性问题分析也具有一定的参考价值。
数值流形方法;高阶多项式覆盖函数;大位移;速度公式;广义自由度
doi:10.11988/ckyyb.20150343
1 研究背景
作为计算力学的经典和普遍使用的方法,有限元法广泛应用于实际工程计算和科学研究中已长达数十年,其特点是以待求的场变量作为网格结点上的未知数,在结构应力分析中表现为位移自由度。近年来在有限元法的基础上,数值流形方法[1]、扩展有限元[2]、广义有限元[3]等新方法,通过在结点处增加广义自由度来提高计算精度,在结构的小变形应力分析中取得了满意的效果[4-6]。
在上述新方法中,数值流形方法率先进入了大位移或大变形的几何非线性问题研究领域。研究表明,在结点上引入除常数位移场变量以外的多项式函数后(被称为高阶数值流形方法),这种广义自由度对计算结果的影响逐渐显现出来。作者在高阶数值流形法的大变形静力分析中曾指出[7],有必要在应力累积中考虑构形坐标的变化,并相应地提出了高阶初应力公式,通过悬臂梁大变形静力分析的计算结果得到了验证。
进一步讨论,如果分析大位移条件下的高阶数值流形法的动力问题,在速度计算中是否也需要进行特殊处理呢?对于此问题,目前的研究均未涉及到,本文通过一个简单例子展开讨论。
为使读者对数值流形方法中的广义自由度有所了解,以下首先简要介绍高阶数值流形方法。
2 高阶数值流形方法简介
数值流形方法[1](以下简称流形法)是我国留美学者石根华博士利用现代数学中流形分析的有限覆盖技术建立起来的一种新的数值分析方法,具有广阔的发展前景。流形法引入2套覆盖网格:一是用于构造物理场近似解的数学网格;另一个是表示材料边界、用于定义积分区域的物理网格。2套网格相互独立,只要求前者在空间上完全包容后者。
流形法对各个覆盖独立定义覆盖函数,通过联络函数(又称权函数)将各个独立覆盖函数连起来形成总体的覆盖函数。规定覆盖Ui上的局部覆盖函数为ui(x)(x∈Ui),它可以是多项式级数或其他级数,随着级数项数的增加及阶数的提高,计算精度得以提高。这些覆盖函数用权函数联系起来,其含义是加权平均,权函数满足

因此总体覆盖函数为

式中n为覆盖总数。
现有的流形法多采用有限元网格来定义数学网格,与有限元任一结点相连的所有网格形成一个数学覆盖,局部覆盖函数定义于结点上形成结点覆盖。这样,任一原始的有限元网格就是各结点覆盖的重叠部分,在此重叠区域(即有限元网格)内,覆盖的权函数取为有限单元的形函数。本文以三角形数学网格为例,其形函数为面积坐标表示的一阶多项式Li(下文统一用上标表示结点序号,注意与指数相区别,用下标n-1,n,n+1表示构形序号)。
考虑在各个结点覆盖上采用一阶多项式的局部覆盖函数,即

式中的a至f为多项式系数,即待求未知数,可以看出,这些未知数已没有通常意义下的位移自由度的物理含义,因此被称为广义自由度。
三角形网格内的位移函数如式(3)所示,结点覆盖函数用三角形网格的形函数连接成为二阶多项式函数,即
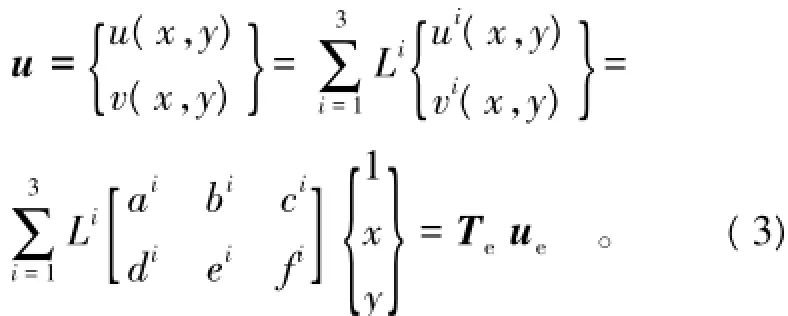
式中Te为网格内的插值函数(三角形网格的形函数与各单项式函数1,x,y之乘积)为以ai至fi表示的网格自由度向量。
与有限元法一样,流形法通过最小势能原理建立平衡方程来进行材料的变形和应力分析,不同之处仅在于位移近似函数的表示方式。文献[8]指出,流形法的动力分析采用了经典的NewMark公式,只是将参数定为β=1/2和γ=1。其动力影响反映在惯性力引起的刚度矩阵(即通常所指的质量矩阵)和荷载向量上,后者包含速度[1]。第n步计算完毕后,n+1步的初始速度为[1]
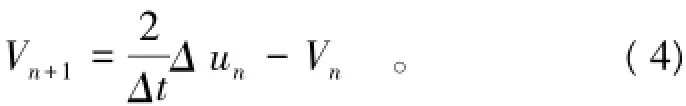
式中:Vn为第n步的速度;Δ un为第n步的增量位移;Δt为时间步长。
对于采用一阶多项式覆盖函数的高阶流形法而言,其结点的速度覆盖按式(4)计算后也具有式(2)的形式,同时,网格内的速度分布具有式(3)的形式,只是系数不同。
高阶流形法由于在结点处引入了带有广义自由度的多项式覆盖函数,因而构形坐标的变化会对材料体的特征量(如应力、速度)产生影响。作者已在文献[7]中对高阶流形法的初应力公式进行了修正,取得了很好的效果。以下针对速度问题,以刚性杆件的匀速旋转为例进行讨论。
3 高阶流形法速度公式存在的问题
如图1所示,采用二维流形元网格计算刚性杆件,杆件长10 m,矩形截面的高度和宽度均为1 m。按平面应力计算,弹性模量取大值以模拟刚性。杆件的左端中点为固定约束,从图示的位置开始按1 rad/s的角速度顺时针旋转,计算步长为0.01 s。

图1 刚性杆件及其流形元网格Fig.1 A rigid bar and its NMM meshes
在文献[9]编制的静力分析程序的基础上增加动力计算部分,分别取覆盖函数为0阶(即常规的位移自由度)和式(2)的一阶多项式,计算图1的杆件转动,得到的杆件自由端中点的坐标如表1所示。

表1 原始方法的杆件自由端中点坐标Table 1 Coordinates of the middle point at the free end of bar(conventional method)
表1中可见,0阶计算结果与理论值(x= 10cos(t),y=-10sin(t))很接近,说明对于刚体旋转运动,用0阶计算就已足够准确。而在同样条件下,一阶计算结果与理论值没有可比性,旋转速度明显快于理论值。这表明,当引入一阶广义自由度时,高阶流形法的速度存在问题。
为便于分析,下面以一维问题为例进行讨论。见图2所示的一个一维网格。在第n-1步时结点1的初始位置为x1n-1,结点2的初始位置为x2n-1,网格内任一点的坐标为xn-1。位移计算完毕后,按式(4)计算得到的结点1和结点2的速度覆盖函数即第n步的初始速度)分别为:

式中a-1n,a-2n,b-1n,b-2n为构形变化前的多项式系数,则一维网格内任意点的速度为

式中N1,N2分别为对应于结点1和结点2的一维网格形函数。

图2 从第n-1步移至第n步的一维网格Fig.2 Schematic diagram of one-dimensional mesh moving from the(n-1)thstep to the nthstep
如图2所示,在进行第n步计算前,根据计算得到的位移量Δu将材料体从第n-1构形更新至第n构形,附着在材料体上的数学网格结点随材料体移动至新的结点位置x1n和x2n,网格内的任一点由xn-1移至xn。若按原始的高阶流形法速度公式,结点1和结点2的第n步速度覆盖函数分别为其中,在构形更新过程中的多项式系数保持不变,即。考虑到刚体运动中的形函数N1和


作为第n步计算的初始速度。然而表1表明,这种速度处理是不正确的。
实际上,材料的构形坐标发生了变化,即
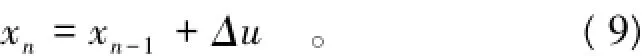
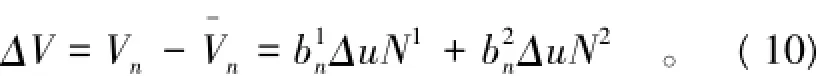
从以上分析可知,由坐标移动产生的速度误差正是造成表1中的一阶速度计算结果不正确的原因,因此需要对高阶流形法的速度进行修正。
4 高阶流形法速度公式的修正
高阶流形法速度公式的修正考虑以下3种方法。
4.1方法1——结点覆盖上的速度修正
比较式(8)与式(6)可见,欲使Vn=V-n,则

考虑到式(11)中的Δu随网格内的材料点位置而变化,作为一种近似,在上述公式中可取结点处的Δu1和Δu2,即结点上的覆盖多项式系数修正为

推广到二维问题,设结点i(i=1,2,3)的第n步速度覆盖函数为

式中ain至fi
n等为系数,三角形网格内的速度分布为

其中Lin为在第n步构形下的三角形网格形函数。
与一维情况的式(10)类似,相对于V-n的速度差值为

设三角形网格第i结点的位移增量为Δui和Δvi,相应于一维公式(12),二维第n步的速度公式为

式中a-i
n至-fin为构形变化前的多项式系数。
重新计算如图1所示的刚性杆件旋转问题,计算结果见表2,可见相对表1有很大改善,表明了覆盖修正公式的作用。但与理论值相比还有一定的误差,如t=1 s时,x坐标相差约7 cm,y坐标相差约5 cm。显而易见,这是由速度覆盖公式中近似取结点处的Δu和Δv所造成的,而准确的Δu和Δv在网格内应随坐标变化。
4.2方法2——速度荷载修正
仍考虑如图2所示的一维网格。网格内每一点的位移变化为

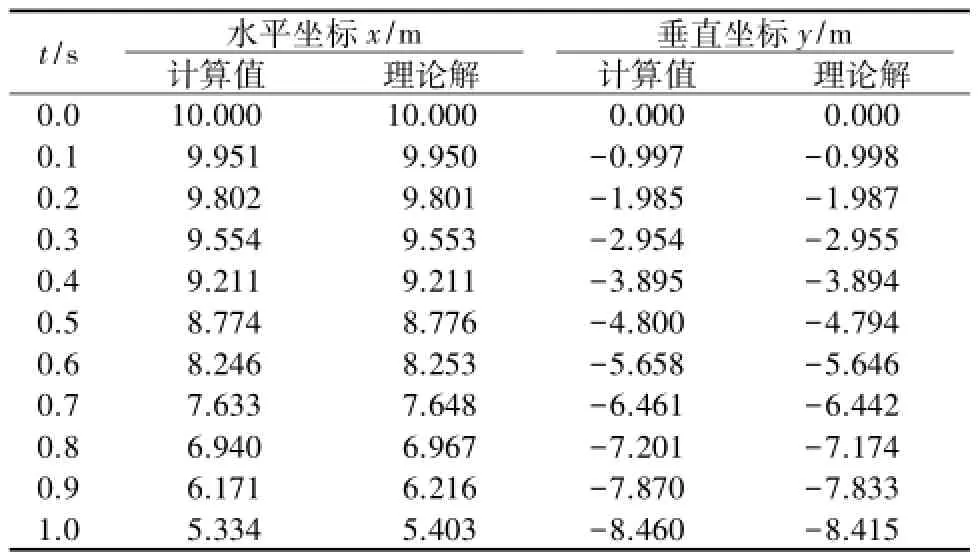
表2 结点覆盖速度修正的杆件自由端中点坐标Table 2 Coordinates of the middle point at the free end of bar(velocity modification of nodal covers)

其中,系数 Δain和 Δbi
n是将它们均与Δ u1和Δ u2有关,这表明速度修正量+已不局限于结点覆盖本身,而与一维网格内的另一结点覆盖有关。对于处在相邻网格的交界点,在不同网格内的速度修正量是不同的,这将造成修正后的速度不连续。
同理,对于二维三角形网格,将

及形函数L1
n,L2n,L3
n的表达式代入式(15)可得

同样,上式中的Δain,Δbin,Δci
n与网格各结点的位移增量有关,对于处在相邻网格的交界处,在不同网格内的速度修正量也是不同的,因此,无法像方法1那样对某一结点的速度覆盖函数进行简单修正,需要寻找其他方法。
考察流形法的基本控制方程,由最小势能原理推导得出[1],其中考虑惯性力的势能表达式(仍以一维问题为例)为
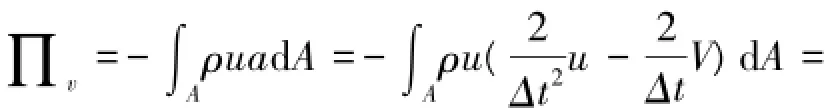
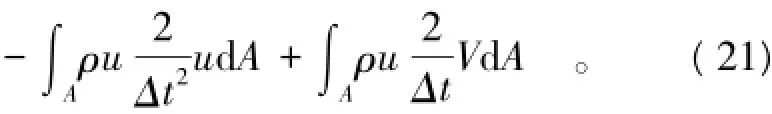
式中:a=2u-2V,为加速度;ρ为密度;A为流形Δt2Δt元面积。考察其中的第2项∫ρu2VdA
AΔt,一般的做法是[1],将网格内的位移u=uTeTTe及速度V=TeVe代入,取极值后得到关于单元速度的荷载表达式为式中:Ve为网格结点速度的广义自由度向量;M= ∫Aρ TTeTedA为单元质量矩阵。

实际上,式(22)为单元的积分表达式,只要求计算Fv的积分,并未要求将V写成包含结点速度的广义自由度向量Ve的形式。可以仅将u=uTeTTe代入并取极值得这就给网格内的速度修正(而不是结点速度修正)提供了依据。

修正后的速度荷载为
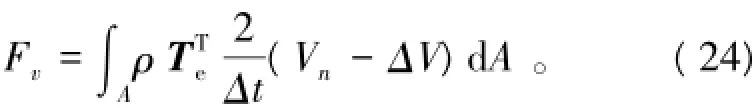
由于在计算速度荷载Fv时进行了速度修正,因而得到的增量位移Δ是比较准确的。但式(4)中的Vn仍采用了构形变化前的系数,并没有进行修正,因此计算出来的Vn+1仍然不准确,进而在计算下一步(第n+1步)的Fv时产生误差而生成不平衡荷载。
下面考虑一种方法,在本步(第n步)式(24)的Fv中对速度增加一个修正量αΔV(α为系数),成为Vn-ΔV+αΔV,使得计算出的增量位移Δ un包含对Vn的修正,从而预先消除上述不平衡荷载。由于流形法计算要求每步的增量位移很小,这样,相邻计算步的速度变化量也很小,因此,基于Vn+1≈Vn的假设,式(4)可看成即2 V对应于,可见,由修正量αΔV引起的
nFv荷载,其计算出的位移值Δ un,是对Vn的修正量的2倍。因此,系数α应取为0.5。
再计算刚性杆件旋转,计算结果见表3,可见相对表2又有很大改善,与理论值更接近。
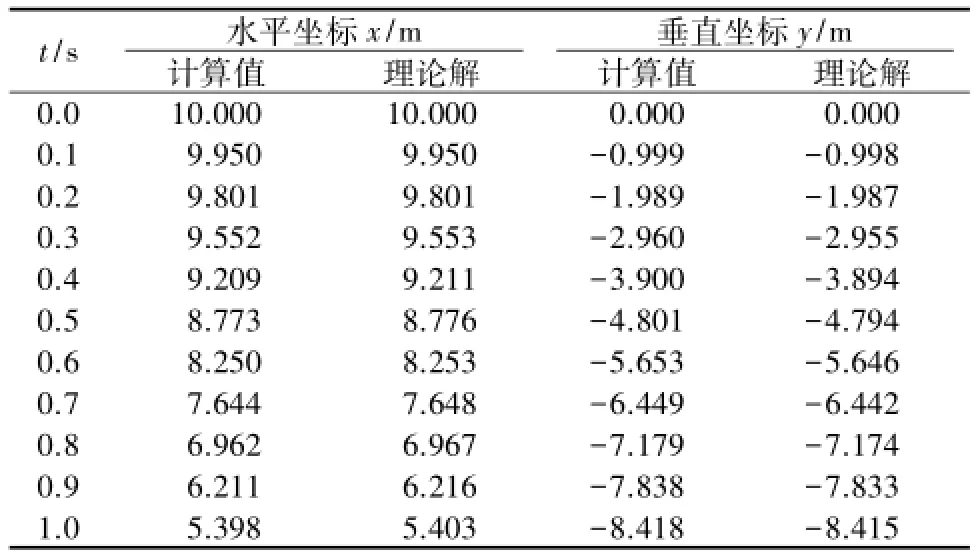
表3 速度荷载修正的杆件自由端中点坐标Table 3 Coordinates of the middle point at the free end ofbar(modification of velocity loads)
4.3方法3——网格速度修正
对上述思路进一步扩展,认为同一结点在不同的网格中的速度不同,即速度不再连续。计算程序不再以结点的形式记录速度,而以网格内的速度信息来记录,即使是连接相邻网格的同一结点,它在各网格内记录的速度信息也是不同的。
对于二维三角形网格情况,按式(20)计算网格内的结点速度修正量,对网格内的各结点Vn直接进行修正(对于同一结点,在不同网格内的修正值不一样),然后代入式(23)计算速度荷载。该步计算完毕后,基于网格内的速度值按式(4)计算新的速度。
刚性杆件旋转的计算结果见表4,在保留小数点后三位有效数字时,与0阶的计算结果完全相同,说明已经完全排除了线性项误差的影响。

表4 网格速度修正的杆件自由端中点坐标Table 4 Coordinates of the middle point at the free end of bar(modification of mesh velocities)
5结语
对于采用一阶多项式覆盖函数的高阶流形法,本文提出了3种速度修正方法:
方法1(结点覆盖修正)最简单,但计算精度较差;方法2(速度荷载修正)的计算精度基本令人满意,并能保持速度场的连续性,但要求相邻计算步的速度差别小;方法3(网格速度修正)计算精度最高,但速度在相邻网格间有间断,不再保持连续性。3种方法各有优缺点,在实际计算中可视情况选用。二阶或更高阶多项式覆盖函数情况,可采用类似方法。另外,本文的研究是针对采用整体坐标来表示多项式覆盖函数时所产生的高阶速度问题,若采用局部化的覆盖函数形式[10],也许会减弱甚至避免上述问题,这还需进一步研究。
在结点处增加广义自由度的各种方法中,数值流形方法已在大位移和大变形的计算中领先一步,本文方法对于其他具有广义自由度的方法(如广义有限元)也具有一定的参考价值。
致谢:感谢数值流形方法的发明者石根华博士的指导。感谢国家自然科学基金(10772034)的资助。
[1] 石根华.数值流形方法与非连续变形分析[M].裴觉民,译.北京:清华大学出版社,1997.
[2]DUARTE C A,BABUSKA I,ODEN J T.Generalized Finite Element Methods for Three-dimensional Structural Mechanics Problems[J].Computer&Structures,2000,77:215-232.
[3]DAUX C,MOES N,DOLBOW J,et al.Arbitrary Branched and Intersecting Cracks with the Extended Finite Element Method[J].International Journal for Numerical Methods in Engineering,2000,48:1741-1760.
[4] 张湘伟,章争荣,吕文阁.数值流形方法研究及应用进展[J].力学进展,2010,40(1):1-12.
[5]李录贤,王铁军.扩展有限元法(XFEM)及其应用[J].力学进展,2005,35(1):5-20.
[6]李录贤,刘书静,张慧华.广义有限元方法研究进展[J].应用力学学报,2009,26(1):96-108.
[7]苏海东,崔建华,谢小玲.高阶数值流形方法的初应力公式[J].计算力学学报,2010,27(2):270-274.
[8] WANG C Y,CHUANG C C,SHENG J.Time Integration Theories for the DDA Method with Finite Element Meshes [C]∥SALAMI M R,BANKS D.Proceedings of the First International Conference on Analysis of Discontinuous Deformation.Analysis(DDA)and Simulations of Discontinuous Media.Berkeley,CA:TSI Press,Albuquerque,NM,1996:263-287.
[9]苏海东,谢小玲,陈琴.高阶数值流形方法在结构静力分析中的应用研究[J].长江科学院院报,2005,22(5):74-77.
[10]林绍忠,祁勇峰,苏海东.数值流形法中覆盖函数的改进形式及其应用[J].长江科学院院报,2006,23(6):55-58.
(编辑:王慰)
Velocity Equations for High-order Numerical Manifold Method
SU Hai-dong
(Department of Material and Structure,Yangtze River Scientific Research Institute,Wuhan430010,China)
Computational accuracy of structure deformation can be improved greatly by the high-order Numerical Manifold Method(NMM).However,poor accuracy or even incorrect velocity results were obtained in the dynamic analysis involved in large displacement.Based on 2-D triangular mathematical meshes and 1-order polynomial cover functions,the reason of the above cases is discussed through an example of rotation of a rigid bar in this paper.Three treatments and the corresponding equations for high-order velocities are presented for the first time,reflecting the change of configuration coordinates under large displacement.The high-order numerical manifold method is useful to other methods such as Generalized Finite Element Method(GFEM)which introduces generalized freedoms at nodes when solving geometric nonlinear problems.
Numerical Manifold Method(NMM);high-order polynomial cover function;large displacement;velocity equation;generalized degree of freedom
O33;O34
A
1001-5485(2016)07-0121-05
2015-04-22;
2015-06-04
国家自然科学基金项目(10772034)
苏海东(1968-),男,湖北武汉人,教授级高级工程师,博士,主要从事水工结构数值分析工作和计算方法研究,(电话)027-82927167(电子信箱)suhd@mail.crsri.cn。
