一类具有强食饵和弱食饵的捕食系统分析

贾建文,杨 航

(山西师范大学 数学与计算机科学学院,山西 临汾 041004)

0 引言

在生态数学中,捕食者与其食饵之间的动力学一直以来都是十分重要的研究课题.Lotke-Volterra模型是最基本的捕食模型.关于Lotke-Volterra模型的研究已经有许多成果[1-4].在捕食系统中,影响模型的动力学因素有很多,其中最重要的一个是功能性反应函数.现有文献中采用的功能性反应函数主要有Holling I-IV型[5-7]、Beddington-DeAngelis型[7]和比率依赖型[8-9]等.近几年，不少学者关注多种群捕食系统的研究[1,3,5,7,10],其中文献[5]建立了两食饵种群(分别为强食饵与弱食饵)与一捕食者种群的捕食系统,研究了该系统平衡点的渐近稳定性及系统持久性.

在生态系统中,捕食者对食饵的捕食率往往不仅依赖食饵,而且依赖捕食者的数量.因此在文献[5]的基础上我们假定捕食种群对强食饵种群的捕食率符合比率依赖功能性反应函数,建立如下模型:

(1)

1 系统解的正有界性

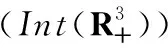
定理1S是系统(1)的一个正向不变集.

因此,对于任意的t>0,系统(1)的任意解均满足x1(t)≤k1.同理可证x2(t)≤k2.

根据系统(1)可得:

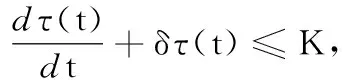
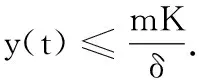
2 平衡点的稳定性

经过简单计算可知,系统(1)存在的平衡点:

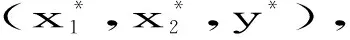
当r1n1k2且r2>n2k1时,平衡点E1存在.

当δ<βηk2时,平衡点E2存在.

(2)

其中

α1=n1n2k1k2-r1r2,β1=βηk2n2,α2=Bβn1k1k2,

β2=Bμr2+Bβ2ηk2,

α3=r1k1r2-n1k1k2r2,β3=δr2-Amr2-βηr2k2,

α4=Br1k1r2-Ak1r2-Bn1k1k2r2,

β4=Bδr2-Bβηr2k2,

α5=-Br1r2+βn1k1k2+Bn1n2k1k2,

其次，教学中教师把主题图换成了点子图（图3、图4）发给每个学生，学生可以根据自己的要求摆放每张点子图。通过点子图的摆放，学生化静为动，通过摆放点子图的位置，理解不同方法的含义。再通过对比寻找到三种方法的相同与不同，让学生们更深刻理解每种方法，提升了学生的思维。在学生的脸上，教师看到了喜悦的笑容。

β5=μr2+Bβηk2n2+β2ηk2.

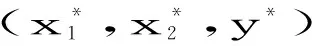
下面讨论各平衡点的局部渐近稳定性.利用特征值方法，易得下面结论成立：

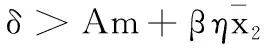
定理6 假设系统(1)的正平衡点E*存在.若满足q1>0,q2>0,q3>0且q1q2-q3>0,则E*局部渐近稳定(q1,q2,q3在定理证明中具体给出).

证明系统(1)在平衡点E*处的Jacobin矩阵的特征方程为

λ3+q1λ2+q2λ+q3=0,

(3)

其中

因此,在定理的条件下，正平衡点E*局部渐近稳定.证毕.

定理7 假设系统(1)的边界平衡点Ek1,E1,E2与E3均存在.若

则系统(1)的这些平衡点都是不稳定的.

选取恰当的正常数u1,u2,u3使下面的不等式成立.

φ(Ek1)=u2(r2-k1n2)+u3(Am-δ)>0,

(4)

(5)

由定理条件可知,当u3充分大时,有φ(Ek1)>0成立.同理,根据定理7的条件，可证明上面各不等式成立.因此,系统(1)的平衡点Ek1,E1,E2和E3都是不稳定的.证毕.

3 持久性与全局稳定性

引理2[10]若p,q>0且

则

定理8 若Br1>A+Bn1k2,r2δ>βmK+n2k1δ,ηβL2>δ,则系统(1)是持久的(其中L2在证明过程中具体给出).

证明由定理1知,只需证明对系统(1)的任意解存在正下界.

根据系统(1),可得

根据引理2,可得

由条件可得L1>0,L2>0,L3>0.因此,系统(1)是持久的.证毕.

定理9 假设系统(1)的正平衡点E*存在.若ρ(0,L3)≥0,则E*全局稳定,其中

证明构造Lyapunov函数:

(6)

其中vi(i=1,2,3)为待定正常数.G(x1,x2,y)沿着系统(1)的解关于t求导,可得

取

从而,当ρ(0,L3)≥0时

进而可得系统(1)的正平衡点E*全局稳定.证毕.

4 数值模拟

限于篇幅，这里仅给出E*的数值模拟和变量n1对各种群规模的影响.

令r1=13,r2=15,k1=200,k2=100,A=0.08,B=0.01,n1=0.1,n2=0.02,β=0.1,μ=0.005,δ=0.01,η=0.02,m=0.2.通过计算可得E*=(94.427 3,68.381 1,28.542 8),易验证定理6的条件满足,则E*局部渐近稳定(见图1).

令r1=13,r2=15,k1=200,k2=100,A=0.08,B=0.01,n2=0.02,β=0.1,μ=0.005,δ=0.01,η=0.02,m=0.2且初始值为(6,2.5,2.5).改变参数n1的值，分别取n1=0.008,0.03,0.05,0.1,0.15,如图2可知,随着n1的增大,强食饵种群x1规模减小,但是弱食饵种群x2与捕食种群的规模增大.

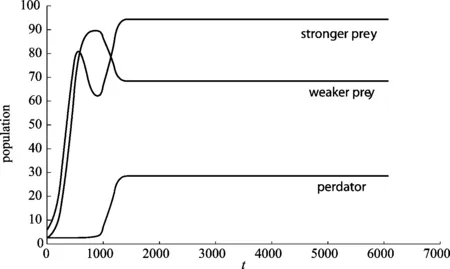
图1 平衡点E*的时间序列图

图2 参数 n1对各种群规模的影响

5 结论

本文研究了一个捕食者与两个食饵的捕食系统(1)，其中捕食种群对(强、弱)食饵捕食率不同，分析了系统(1)解的有界性及可能平衡点的存在条件，通过特征值的方法证明了平衡点的局部渐近稳定性.进一步,我们讨论了系统(1)的持久性,并通过构造Lyaupunov函数证明了正平衡点E*的全局稳定性.最后,通过数值模拟验证了所得结论的正确性，说明了变量n1和n2对各种群规模的影响.