矩阵的幂零对角分解及推广
2016-08-08姜琴袁力
姜琴,袁力
(汉江师范学院计算机科学系,湖北十堰442000)
矩阵的幂零对角分解及推广
姜琴,袁力
(汉江师范学院计算机科学系,湖北十堰442000)
摘要:幂零矩阵及其性质在矩阵理论中有着重要应用。重点讨论了n阶方阵与幂零矩阵之间的关系问题,证明了任意n阶方阵可以分解为1个幂零矩阵与1个可对角化矩阵之和,并将该结论推广到了矩阵多项式上。最后,应用上述矩阵分解定理的证明思想,进一步给出了n阶方阵的对称矩阵分解形式。
关键词:幂零矩阵;对角分解;若当分解
1概述
幂零矩阵因其特殊的性质及其在组合数学、矩阵谱分析中的重要应用,成为近年来比较热门的一个研究方向,也取得了众多的研究成果。
文献[1-2]给出了构造幂零矩阵与谱任意符号模式矩阵的几种方法;文献[3]利用主子式刻画了在没有幂零元的坡上幂零矩阵的一些特征;文献[4-5]讨论了一般加法幂等半环上矩阵的同时幂零性及标准形;文献[6]对幂零线性变换生成的幂零代数及其同构问题进行了讨论;文献[7]给出了阶幂零矩阵的判定方法与构建方法。
本文将在上述结论的基础上,进一步考虑一般阶矩阵的幂零分解问题,对已有的结论予以补充。
2主要结论的证明
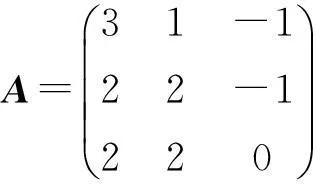
题目要求证明所给3阶矩阵可以分解为1个幂零矩阵与1个可对角化矩阵之和的形式。下面运用矩阵的对角化方法先给出此问题的证明。
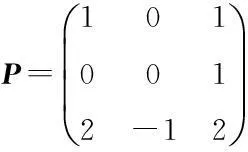
由上述证明可知,所给3阶矩阵A可逆,且可以分解为幂零与可对角化矩阵之和的形式,那么这种分解能否推广到一般的n阶矩阵上来呢?现在来看下面的结论。
通过微生物形态学鉴定及全自动鉴定系统,对照组中约60%为表葡菌。鼻渊舒口服液治疗前两个地区CRS患者中约61.1%为表葡菌;治疗后约63.8%为表葡菌(具体细菌分布见表1、图1)。
定理1设A为n阶方阵,则存在矩阵B和C,使得A=B+C,且BC=CB,其中B相似于对角矩阵,C为幂零矩阵。

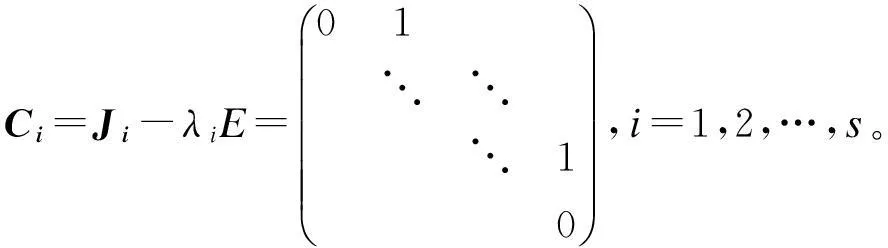
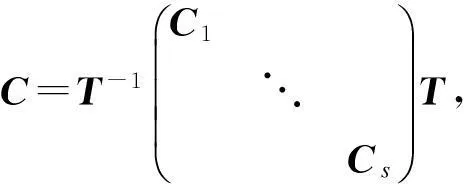
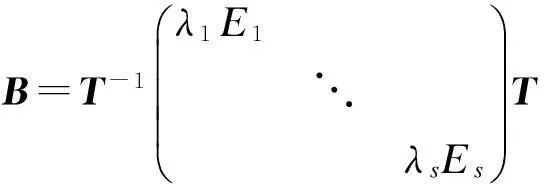
定理1将矩阵的幂零对角分解推广到了任意n阶方阵上来,是对文献[8]结论的补充和完善。
推论1设A为n阶方阵,且秩A=1,则A或为可对角化矩阵,或为幂零矩阵,二者不兼有。
证明因秩A=1,则可知矩阵A有0特征值,且齐次线性方程组AX=0的解空间是(n-1)维的,故属于特征值λ=0的特征子空间V0也是(n-1)维的,所以A有n-1个属于特征值λ=0的线性无关的特征向量。
推论1给出了方阵秩为1时的幂零对角分解形式,是定理1的特殊情况。
推论2设A为n阶方程,B是A的可对角部分,则对于任意多项式g(x)∈c[x],g(A)的可对角化部分为g(B)。
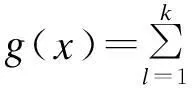
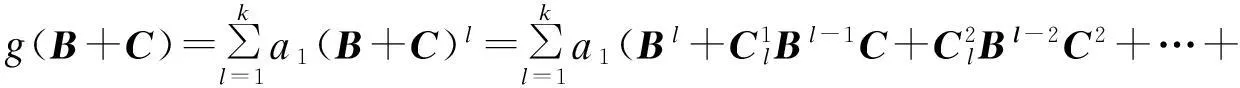
因为BC=CB,所以(BC)n=BnCn=0,故M中的每一项Bl-iC均是幂零的,所以M是幂零的,不能对角化,故g(A)的可对角化部分为g(B)。
推论2将定理1可对角化部分的结论推广到了矩阵多项式上来。同时,应用定理1的证明方法,还可进一步得到如下结论。
定理2设A为n阶方阵,则存在2个对称矩阵B和C,使得A=BC,且B,C中有1个为可逆矩阵。
证明设A为任意矩阵,J为其若当标准形,则存在可逆方阵P,使A=P-1JP,也即J′=(P-1)′A′P′,
再令B=AC-1,即A=BC,则由上式可得
B′=(AC-1)′=(C-1)′A′=AC-1=B
即B也是对称矩阵。
定理2借鉴了n阶方阵幂零对角分解的证明思想,进一步给出了n阶方阵的对称矩阵分解形式。
[参考文献]
[1]DREW J H,JOHNSON C R,OLESKY D D,et al.Spectrally arbitrary patterns[J].Linear Algebra and Its Applications,2000,308(1-3):121-137.
[2]GAO Y,HUANG Y,SHAO Y.The relations of spectrally arbitrary,inertially arbitrary and potentially nilpotent sign patterns [C]//Proceedings of the 14th Conference of International Linear Algebra Society,Shanghai:[s.n.],2007:19-22.
[3]HAN S C,LI H X,WANG J Y.On nilpotent incline matrices[J].Linear Algebra Appl,2005,406(5):201-217.
[4]LUR Y Y,PANG C T,GUU S M.On nilpotent fuzzy matrices[J].Fuzzy Sets and Systems,2004,145(2):287-299.
[5]官明友,谭宜家,李德新.加法幂等半环上矩阵的同时幂零性[J].福建农林大学学报(自然科学版),2009,38(6):668-672.
[6]胡秀玲,张秀福.幂零矩阵和幂零线性变换[J].徐州师范大学学报(自然科学版),2006,24(4):17-18.
[7]吴险峰.阶幂零矩阵的判别及构建[J].齐齐哈尔大学学报,2007,23(4):72-75.
[8]杨浩波.矩阵的幂零分解[J].杭州师范大学学报(自然科学版),2009,8(5):334-337.
责任编辑:陈亮
doi:10.3969/j.issn.1671-0436.2016.03.011
收稿日期:2016- 04- 06
基金项目:湖北省教育厅科研计划资助项目(Q20156002);汉江师范学院科研重点项目(2014A02)
作者简介:姜琴(1978—),女,硕士,讲师。
中图分类号:O151.2
文献标志码:A
文章编号:1671- 0436(2016)03- 0048- 04
Nilpotent Diagonal Factorization of Matrix and the Extensions
JIANG Qin,YUAN Li
(Department of Computer Science,Hanjiang Normal University,Shiyan 442000)
Abstract:Nilpotent matrix has important application in matrix theory.The relationship between square matrix of degree n and nilpotent matrix was explored,which testifies that square matrix of degree n can be decomposed into the sum of nilpotent matrix and diagonalization matrix.This decomposition can be applied in any matrix polynomial.Finally the above testifying method provides decomposed form for symmetric matrix of square matrix of degree n.
Key words:nilpotent matrix;diagonal factorization;Jordan decomposition
