弯曲钢油管外载荷测试方法研究
2016-08-08文智胜熊耀志
文智胜,熊耀志
(广西柳工机械股份有限公司,广西 柳州 545007)
弯曲钢油管外载荷测试方法研究
文智胜,熊耀志
(广西柳工机械股份有限公司,广西 柳州 545007)
摘要:工程机械产品的弯曲钢油管有时会出现疲劳断裂的现象,为了对其进行优化,用有限元分析现有结构的应变分布并进行结构改进是一种有效的解决方法。但是,钢油管在实际工作过程中所受到的外力较为复杂,要在有限元模型上施加仿真边界条件会遇到困难。通过对钢油管进行受力简化,并用试验的方法,以应变片为工具测量出确定加载力下的应变响应,然后对测得的数据进行分析,建立外载荷与测点位置应变间的关系方程,最终结合实际工况可达到以应变响应测出外载荷,提供有限元分析的边界条件的目的。这一方法可应用到各种工程产品中。
关键词:载荷;弯曲油管;测试方法;工程机械
1前 言
弯曲钢油管普遍用在工程机械产品上,影响产品的性能与安全性,对于工程机械产品的正常稳定运行起着重要作用。对出现断裂的钢油管结构进行改进时,往往因其外力受载情况难以确定而无法取得进展。钢油管在产品上受到的载荷可能有:因进油口压力产生的对油管的方向拉/压力(可能产生弯曲和扭曲),产品发动机激励产生的振动;油管自身内部的液体压力等。如果只对钢油管内部压力的影响进行分析,会忽略很多载荷因素的影响,怎么确定这些载荷因素是获取钢油管有限元分析边界条件的主要问题。
阎楚良、张书明等用应变片的方法,通过组建多个电桥,建立了飞机机翼、尾翼结构件和导弹挂架载荷输入与应变输出关系方程,获得飞行过程中载荷的时间历程[1-2],标定出的是结构中弯曲、扭曲、剪力等内载荷,而非外力。借鉴以上两项工程实践经验,应用应变测试方法对弯曲钢油管所受外力进行测试标定,根据油管自身的特点,通过分析加入油管内压的影响,使得关系方程更为完善,为结构改进提供试验依据。
2力学模型
2.1受力分析
弯曲钢油管的失效断裂部位一般是在固定一方的连接焊缝附近,重点是要分析弯曲部分所受到的力。下面是一个弯曲90°的钢油管,根据它装在工程机械产品上的状态,建立如图1(1)所示的力学模型。钢油管B面固定,A、C、D面分别受到3个方向的力Fx、Fy、Fz的作用,E面有内压p。
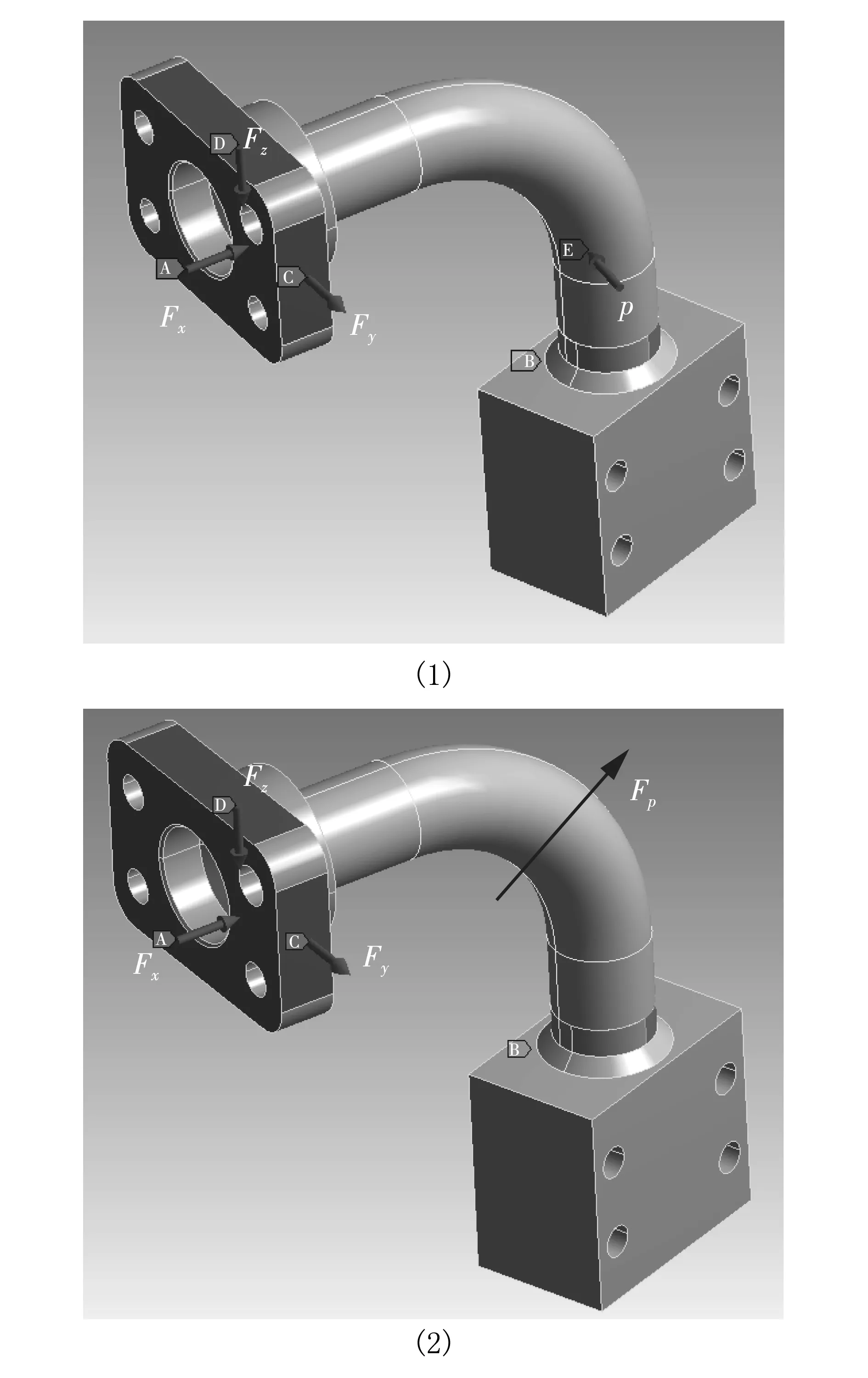
图1 力学模型
弯曲钢油管弯曲部分因弯曲内径和外径不同,存在径向面积差,内压p的存在,导致其弯曲部分总体受到一个径向的力Fp(如图1(2)所示),使弯管有变形趋势。图1(1)和图1(2)的受力情况对于钢油管弯曲部分是等效的,下面用积分计算证明这一结论。
2.2内压对弯曲部分的影响
如图2所示,假设有一个一端固定在y轴上的弯曲90°的钢油管,只受到静内压p的作用。横截面垂直于Ⅱ轴方向的压力因结构对称而相互抵消,垂直于Ⅰ轴方向上因弯曲内外径产生的面积差而受到压力作用,方向为沿横截面径向指向弯曲外径,在ds面积内大小为dF,整个弯曲部分受力为F。


图2 弯曲部分分析


=2pr2sin2αdαdβ
整个弯曲部分的压力是dF在整个弯曲面积上的积分,也就是dF-dF′在α从0到180°、β从0到90°上的累加。为便于计算,将dF分解成x方向和y方向上的两分量dFx和dFy,dFx=dF·cosβ,dFy=dF·sinβ,分别对两个方向上的分量进行积分,因积分域关于Ⅱ轴对称,有:
推导表明,弯曲90°的钢油管在内压p作用下,其弯曲部分因面积差所受的力在x和y方向上的分量都等于内压p与横截面内圆的乘积。
考查弯管上弯曲角度从β1到β2范围内压作用下的受力(如图3所示),可推出下列公式:

图3 弯管受力

=p·πr2(sinβ2-sinβ1)

=p·πr2(cosβ1-cosβ2)
经过用有限元软件建模计算,得到的结果一致。由此,可得出结论:静内压作用下的钢油管因弯曲内外面积不同而最终等效受到一个由内径指向外径的合力,使油管有变形的趋势;该力大小和方向与钢油管的弯曲半径无关,与钢油管的弯曲角度β(从β1到β2)有关;内压p可作为一个力的元素直接加入到受力分析的模型中,即图1所示情况。
2.3应变响应位置选取

图4 建立载荷与应变关系方程选取的位置
力学模型中,有4个力Fx、Fy、Fz、p对钢油管同时作用,需要选取4个应变响应(相当于4个自由度)的位置。因失效部位主要是在固定端的焊缝附近,选取如图4所示的4个位置,作应变考察点,分别考察1、2号点的环向应变和3、4号点的轴向应变。 用选取的应变响应点与所受到的力建立起两者之间的方程关系,测试时就可以用应变片的测量结果推出外载荷的大小。
3数学模型
各位置在多个力作用下的应变是这些力单独作用的线性叠加,假设每个力对各应变位置的影响因子为aij(第j个力对第i个应变的影响),列出方程组:
矩阵形式:
ε=a·F
式中,

阵a-1,矩阵方程可解出:
F=a-1·ε
即能用应变测出外力。下面用有限元的方法来说明上述计算方式(如图5所示)。用图1上的边界条件和图4所选取的应变考察位置,建立钢油管的有限元模型,分别给各个方向单独施加力,计算4个应变位置的相应应变。

图5 力单独加载模型(分别以x方向力和压力示意)
分别单向加载x、y、z向的力4000N和内压4MPa,用所加载的各个方向力和有限元相应计算出的各点应变,列出下列矩阵方程:
为了验证计算结果,在模型上加上一个(FxFyFzp)=(2000150012003)的组合力,有限元模型计算得出的等效应变如图6所示,4个位置的应变(ε1ε2ε3ε4)=(-25.165182.53-215.07346.78)(单位:微应变)。将其代入上述矩阵式,求得(FxFyFzp)=(1999.6 1499.9 1199.8 3.0),说明矩阵结果与有限元结果相符,计算方法合理可行。
4方法应用
通过上述方法, 可以用4个不同位置、方向任意的应变测出等效x、y、z方向力和内压力, 通过有限元计算得到了验证。实际进行试验时,很难做到像有限元这样精确地加载到某一个方向上,两者相比较会存在偏差。可以将试验加载结果作为矩阵计算的依据,有限元则作理论参考。

图6 组合力计算结果
该方法的应用还要注意以下事项:
(1)多次计算证明,矩阵a中的系数只要有一些小变化, 最后计算出的力结果就会有较大影响,矩阵a中的系数应保持足够的精度。
(2)试验应用中所选取的应变位置不应该在应变梯度较大的地方,否则计算结果会不准确。
5结论
经过分析知,弯曲钢油管的内压可等效地转化为其弯曲部分上的一个方向力,建立力学模型时,可添加为一个矢量元素。
可用应变测量出弯曲钢油管的等效外力,为有限元计算分析提供边界条件。改进产品结构,计算矩阵系数精度和良好测点位置需要保证。
参考文献
[1]阎楚良,张书明,卓宁生,等.飞机机翼结构载荷测量试验力学模型与数据处理[J].航空学报,2000,21(6):56-59.
[2]周福强,张书明,阎楚良.导弹挂架载荷标定试验与模型求解[J].机械强度,2009,31(2):221-224.
[收稿日期]2016-05-12
[作者简介]文智胜(1987-),男,工程师,主要研究方向:机械振动、振动疲劳、结构强度。
中图分类号:TG115.5
文献标识码:B
doi:10.3969/j.issn.1674-3407.2016.02.002
Study on Test Method for External Load of Kneed Steel Pipe
Wen Zhisheng, Xiong Yaozhi
(LiuGong Machinery Co., Ltd. Liuzhou 545007, Guangxi, China)
Abstract:Kneed steel pipe of construction machinery products may suffer a fatigue fracture. Strain FEA is an excellent way to simulate existing structure and improve it. How to determine the boundary condition is an encountered difficult due to the complex forces loading on pipes in works. To establish the requisite boundary condition, choose strain gage to be the tool. First, simplify the structure to be mechanical model, and measure the response of strain gages on a serious of known forces. Then establish an equation to link external loads and strain in corresponding spots. At last, measure strains in actual work condition to calculate external loads, which is the boundary condition we need. The test method proposed in the paper can be applied to various construction products.
Keywords:load; kneed pipe; test method; construction machinery
