结合图论的供水管网PMA分区方法
2016-08-08高金良
高金良,姚 芳,叶 健
(哈尔滨工业大学 市政环境工程学院,哈尔滨 150090)
结合图论的供水管网PMA分区方法
高金良,姚芳,叶健
(哈尔滨工业大学 市政环境工程学院,哈尔滨 150090)
摘要:供水管网压力分区(PMA)以压力调控为主,兼顾区域计量,可有效地控制城市管网漏失,为此,提出结合图论的PMA分区方法,首先运用自适应AP聚类算法结合经济性计算对供水管网进行初步分区,确定分区数目;然后运用迪杰斯特拉(Dijkstra)算法计算各个聚类中心点到水源的最短路径,确定各个分区的供水管段;建立分区边界优化模型,运用模拟退火算法求解该模型;最后结合人工经验对部分分区进行适当合并,形成最终方案并运用于Y市供水管网实例,取得良好结果.该种分区方法是以计算机算法为主体并结合人工经验,很大程度降低分区的工作量,并且比传统的人工试错分区具有更大的搜索空间,可用于指导实际供水管网的PMA分区.
关键词:PMA分区;图论;AP聚类算法;迪杰斯特拉算法;模拟退火算法
近年来,供水管网分区成为国内外控漏研究领域的一大热点,国际上普遍认可这种“分而治之”的分区思想.将供水管网进行分区后,能够找到供水管网漏失主要原因,由消极被动转变为积极主动地控漏,有利于加强水质监测及压力管理[1-4].国内外的供水行业学者和研究人员都对供水管网分区控漏进行了积极探究,研究的分区方法主要分为区域计量分区、压力分区和管理分区.其中,压力分区被认为是最具有经济效益的方法.城市供水管网压力分区技术最早起源于20世纪80年代,以供水管网漏损随着水压上升而增大的规律为理论基础,依据地形、水压分布等因素将管网分为若干压力管理区,通过对所有或部分管理区进行压力控制,降低管网的平均压力实现减少管网漏失等目的.May[5]和Godwin[6]指出供水管网中漏失总量与压力呈指数关系,可以通过降低整个管网或局部区域压力来降低漏失水量;Stering[7]将供水管网划分为若干个压力管理区域,通过控制阀门的开启,实现供水管网压力的优化控制.我国对供水管网压力分区的研究起步较晚,崔建国等[8]通过对节点压力、压力变化灵敏度及管网的供水分界线的分析,综合考虑管网布置区的规划和地形情况,对复杂管网进行分区管理;周玉文等[9]提出应综合考虑区域计量分区原则、压力分区原则及管理分区原则进行分区规划的新思路,并对分区改造后的管网进行了模拟分析.
一般来说,管网的爆管率、漏失量、管件及其他设备的故障率均与管网中水压存在正相关性[10].实时掌握管网水压分布情况对于控制管网漏失[11]、降低爆管事故发生率及供水能耗具有重要意义[12],而供水管网PMA分区是压力分区控制的基础.PMA分区是并行分区,区域之间不存在对下一区域串联供水的情况,该情况下形成的分区可以对每个区域单独进行压力控制.同时,与传统的人工试错分区方法相比,PMA分区具有更大的搜索空间,能提高分区适用性.本文结合工程实际,综合运用图论的思想,将供水管网转化为图的结构,对供水管网进行PMA分区.
1PMA分区
供水管网的分区数目直接影响分区方案的优劣.分区数目少,供水管网的压力管理不彻底,会导致许多节点压力过高,降低降漏效果;分区数目多,投资费用增加,且对供水管网拓扑结构造成扰动,易导致供水不稳定.本文用自适应AP聚类算法并结合经济效益对供水管网进行初步分区,确定分区数目.在分区过程中,投资费用主要指安装减压站费用.如图1所示,投资费用与分区数目呈线性关系,经济效益开始随分区数目的增加而增加较快,逐渐增速变缓,因此,投资回报与分区数目的关系呈向下抛物线关系.自适应AP聚类算法由Fery B J和Dueck D于2007年首次提出[13].该算法不需要指定聚类数目,而是在算法运行过程中设定图中所有点到其类中心点的距离之和为目标函数,随着迭代的进行,不断搜索与变换聚类中心点的位置与数目,使目标函数最小[14].本文利用自适应AP聚类算法的特点,合理地确定分区数目,使投资效益最大化.
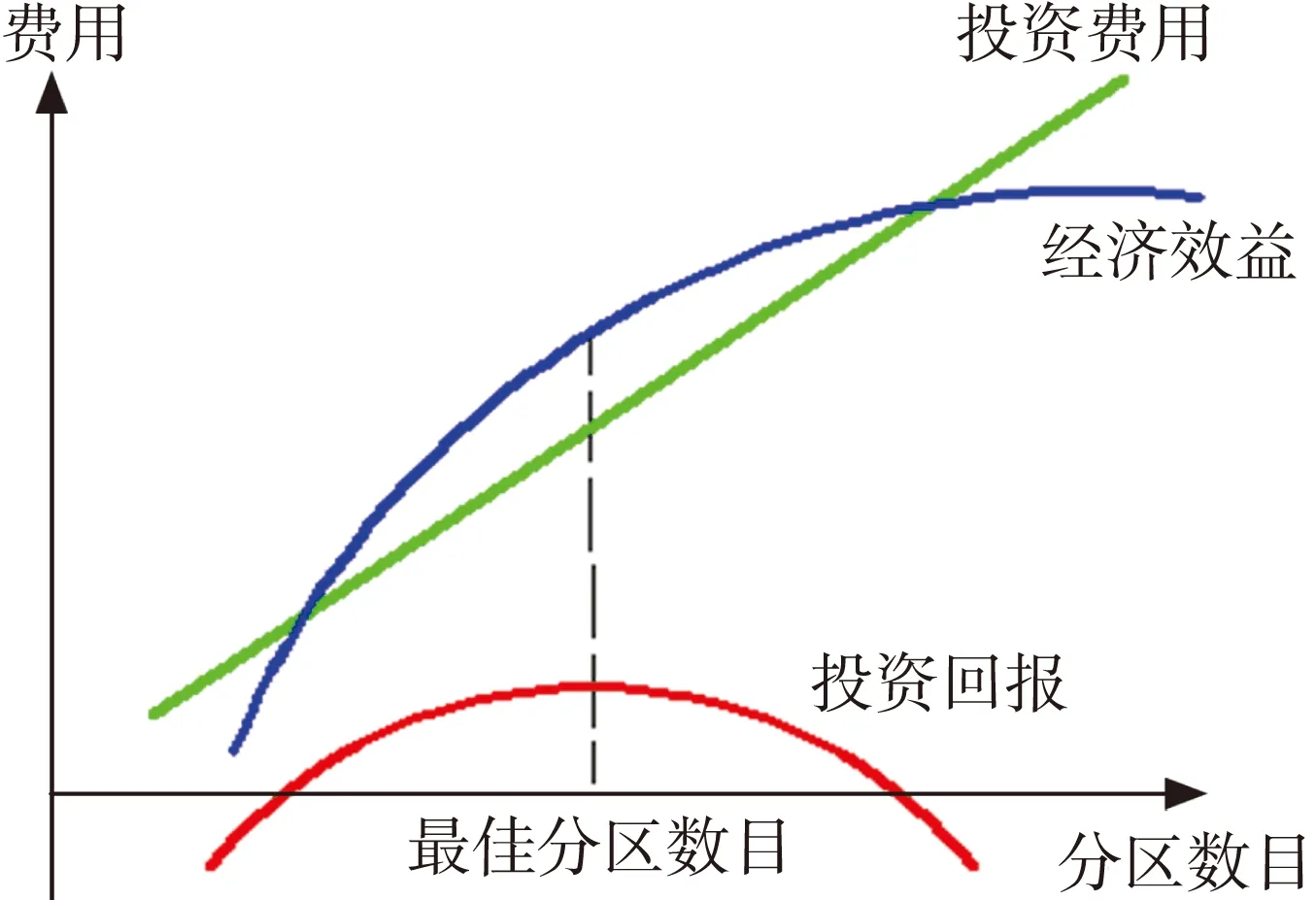
图1 分区数目与投资效益的关系
确定分区数目时,以用水节点的X坐标、Y坐标和自由水头这3个参数进行归一化计算后用于定义节点的三维位置.算法开始时需设定Pi值,通常Pi为i节点与其他所有节点相似度的平均值,也可根据需要自行设定值,值越大则聚类数目越多,反之,值越小则聚类数目越少[15].由于聚类前每个节点都具有成为聚类中心的可能性,开始定义所有节点的Pi均相等.输入这些参数进行第一次聚类运算,得到各个点的类归属和聚类数目,计算各个类中节点所具有的降漏潜力,从而得到这种聚类方案下的经济效益,结合投资回收期确定分区数目是否可行,进而调整P值进行下一次AP聚类,直到计算得出使投资回报期最短的初步聚类方案.
2确定供水管网PMA分区区域入口
供水管网PMA分区是不完全分区模式.本文采用邻接矩阵表示管网拓扑,运用迪杰斯特拉(Dijkstra)算法[16]计算聚类中心到水源的最短路径,并将最短路径定义为各个区域的供水入口.供水管网的主干管部分不进行区域划分,但初步分区时所有节点均参与聚类,最后需剔除节点大多分布在主干管上的区域.计算步骤如下[17]:
1)初始化S集合,此时集合S中只含有单一水源点v0,集合T中则包含拓扑图中除水源点v0外的所有顶点,若供水管网模型中有m个水源,则运用迪杰斯特拉算法分别计算m次;
2)计算集合T中各顶点到水源点v0的距离,将距离最小的顶点u加入到集合S中;
3)计算顶点u到集合T中各顶点的距离,若经过顶点u到顶点t的距离值比原来不经过顶点u到水源点v0的距离值小,则修改t的距离值;
4)重复步骤2)和3)直到供水管网拓扑图中所有的顶点都由集合T转移到集合S中,算法结束.
3区域边界优化模型建立及求解
确定区域入口后,若此时直接对聚类边界进行关阀,将会有大量节点无法供水,这对供水管网扰动太多.此时需要对分区边界进行优化,以减小对管网的扰动,实现分区.
3.1区域边界优化模型
供水管网分区的基本要求是保证其供水安全性,即分区后供水管网中所有节点均能与水源节点连通并保证其供水的连通性.初步聚类后,需要对各个初步分区进行节点连通性判断,通过改变孤立节点的类归属,保证各个分区节点全连通.各个类中的节点全部连通后,可通过边界优化,尽量将分区对管网的扰动程度降到最低.本文建立一个拓扑离散优化模型,以确定分区边界.
1)优化变量.优化模型的变量为分区边界点的类归属.然而分区边界的点并不固定,优化过程中随着某节点类归属的变化,周围节点就有可能从非分区边界点变为分区边界点.因此,该模型以供水管网拓扑图中所有节点的类归属作为优化变量,类归属的数量固定不变,由AP聚类算法得出.所有节点的类归属矩阵如下
(1)
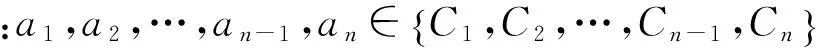
2)目标函数.确定分区边界的目的是使分区可行,因此,需要降低分区对原管网的扰动.此时应尽可能地找出分区边界上流量较小的管段,关闭这样的管段对管网供水影响较小.定义管段流量作为全管网邻接矩阵的权值,目标函数为使所有边界管段的权值之和最小,适应度函数如下
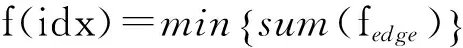
(2)
式中:fedge为边界管段的流量,最短路径管段流量不参与目标函数计算,L/s.
但是上节已建立的各个节点的最短路径结构构成了供水管网最基本的拓扑模式,且最短路径通常会成为区域之间的连接管段.因此,在分区边界优化过程中,为了不干扰优化结果,最短路径管段流量直接记为0.
3)约束条件.优化过程中,可通过保证各个类所有节点的连通性来确保管网的供水安全性,因此,在优化迭代过程中约束条件为每一代聚类中心点与该类内部所有节点的连通性必须保证.
3.2区域边界优化模型求解
建立的模型属于离散变量拓扑优化模型.优化过程中,拓扑节点的属性需要不断改变,并且每次迭代过程需要随机对拓扑节点属性进行扰动,从而挑选出最佳种群进行下一次迭代,模拟退火算法能够很好地解决该问题.模拟退火(simulated annealing)算法是1982年Kirkpatrick等[18-19]提出的一种针对NP完全问题的算法.本节在初步聚类的基础上,将初步聚类结果作为模拟退火算法的初始解,运用标准模拟退火算法优化局部区域(分区边界部分),通过迭代得到最优方案,模拟算法中的相关参数在工程案例中设置.
4分区合并
供水管网分区边界优化完成后,关闭所有的边界管段进行水力计算,此时由于关闭管段过多,极易导致水力条件无法满足用户需求.因此,结合人工经验对部分区域进行合并,保证供水要求.合并形式主要为纵向合并和横向合并.初步分区并计算最短路径后,若有两个聚类中心共用一条供水路径,则对供水管网分区进行纵向合并,以保证主干管直接向所有区域供水,如图2所示;若分区之间连接管段较多,完全关断会导致局部供水压力不足,此时需要对这两个分区进行横向合并,合并后可以两个入口综合控压,也可以再通过最短路径计算出一条供水管线,如图3所示.
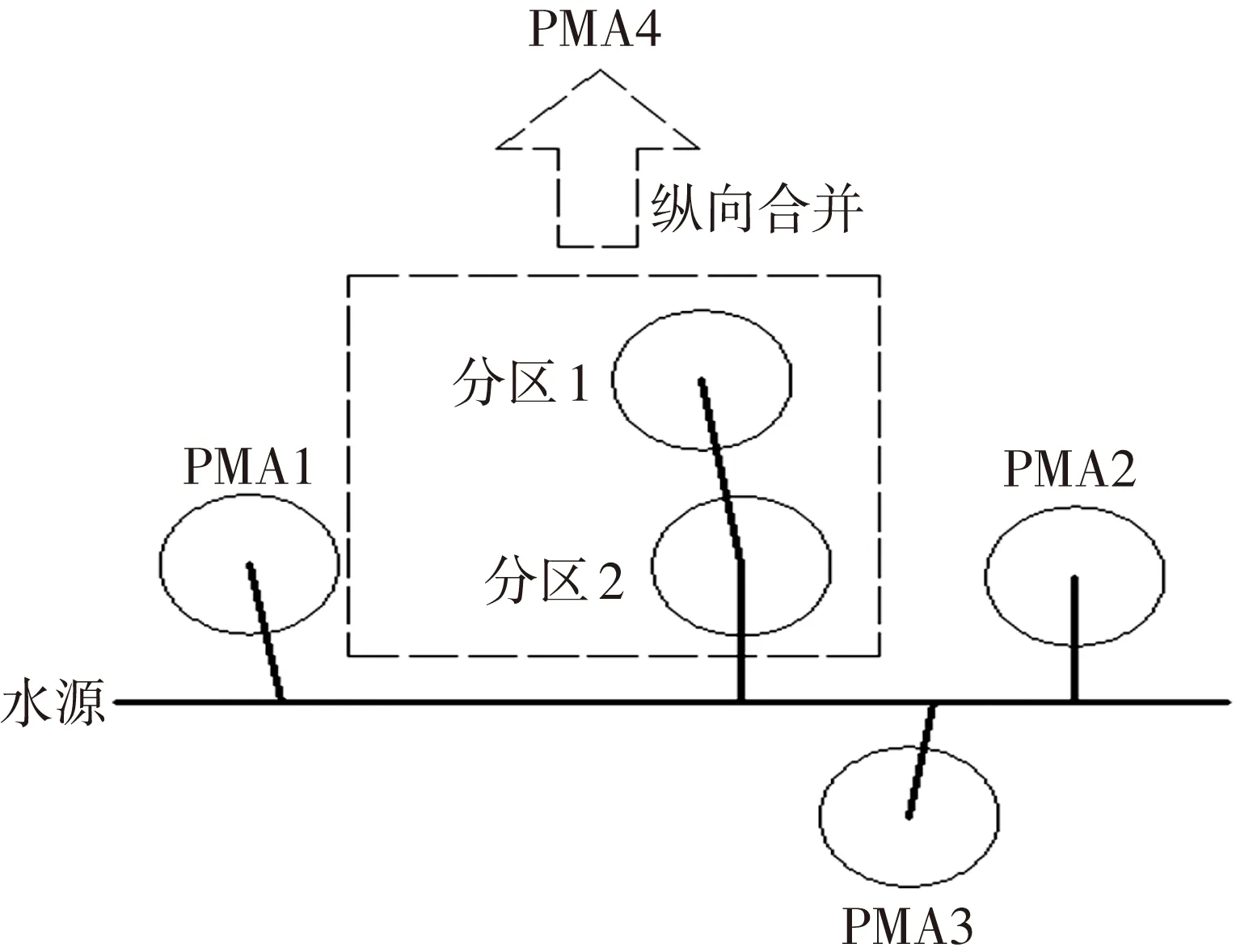
图2 分区纵向合并示意

图3 分区横向合并示意
5工程案例
本文运用Y市的实际供水管网,收集其供水管网运行基础信息,得出最高时和最低时供水管网自由水头分布,结果见图4、5.可以看出,为满足供水管网末端压力供给,整个管网压力偏高.过高的压力是本市漏失严重的重要原因.因此,结合图论对Y市供水管网进行PMA分区,划分出具有降压潜力的区域实施压力控制,探索该方法的可行性与适用性.
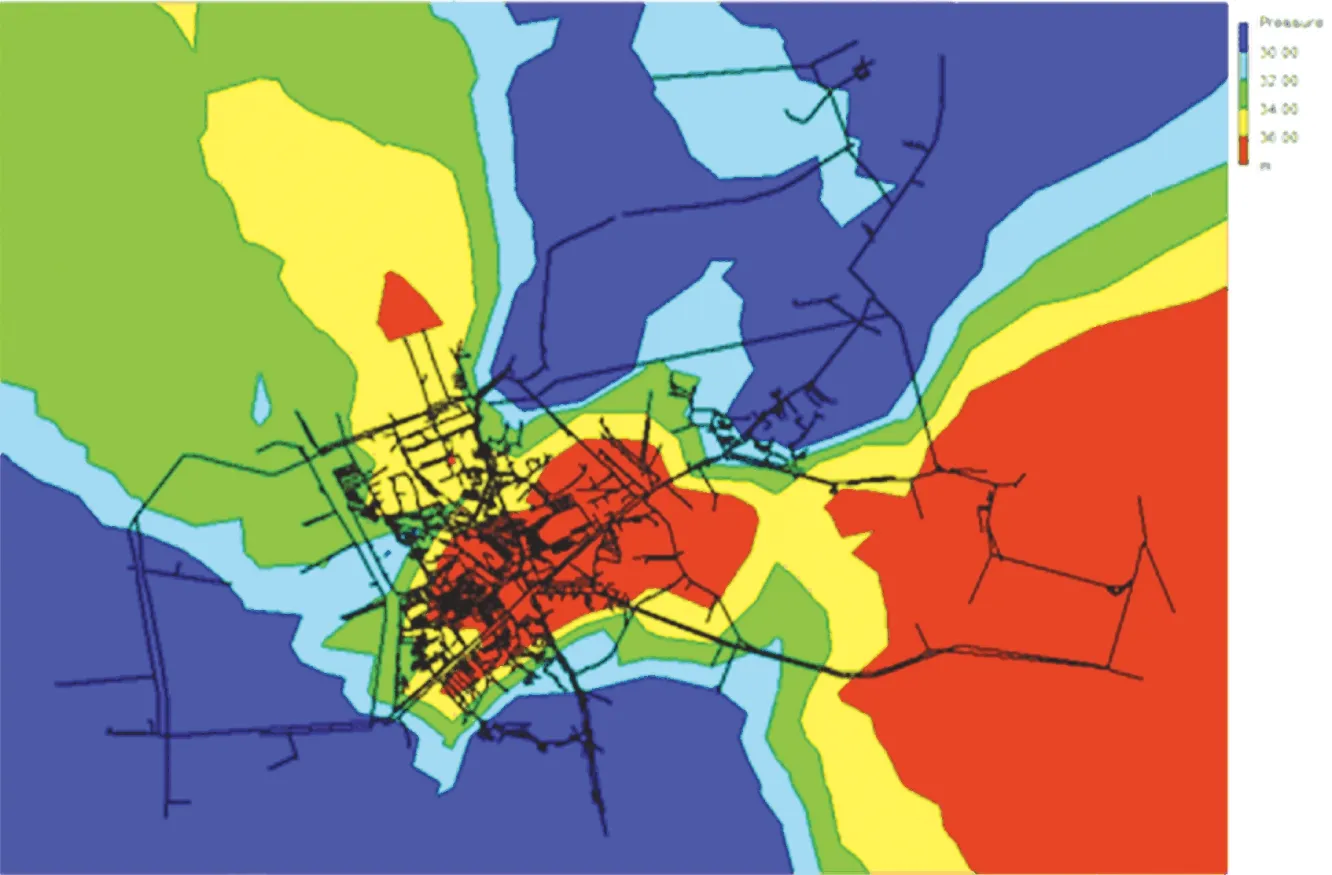
图4 用水最高时供水管网自由水头分布

图5 用水最低时供水管网自由水头分布
5.1AP聚类初步分区确定分区数目
结合实际工程进行调研,Y市水司制水成本为0.65元/t,减压站的购置和安装的总费用为20万元,压力控制设备年运行费用为1万元,当地要求供水压力最低不得低于20 m自由水头.优化过程中,分区数降到20以内时,管道改造费用为0;分区数在20以上时,管道改造费用随着分区数的增加呈指数级增涨.
建立的优化模型变量为自适应AP聚类算法中的P值,优化目标为最大化年经济收益.因为变量单一,运用进退法依次计算P值,P的初始值按AP聚类算法默认值,取-0.063 4,初始步长为0.1,经济函数出现折点后步长逐步减半迭代.最终优化结果:P取值为-2.292 8,投资回收期为1.8 a,分区数为17.优化过程各变量如图6所示.
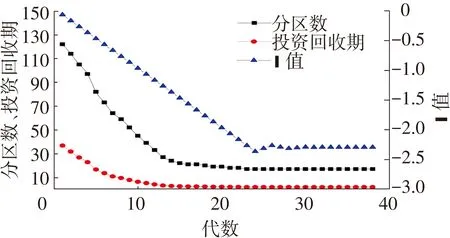
图6 结合AP聚类算法的经济性计算结果
AP聚类算法依据节点的X坐标,Y坐标和自由水头这3个属性进行聚类,P=-2.292 8时,最终得到的初步分区结果如图7所示,管网被划分为17个区域,分别用不同颜色表示.

图7 初步聚类结果
5.2聚类中心点到水源的最短路径
初步聚类得到17个区域的聚类中心后,分别计算17个聚类中心点到水源点的最短路径.将管道的水头损失作为最短路径计算中点与点之间的权值,运用迪杰斯特拉算法计算各个聚类中心点到两个水源的最短路径,最短路径的长度即水头损失之和,结果如表1所示.可以看出,大部分聚类中心点到两个水厂的最短路径均相同,因此,无论从到哪个水源考虑,均不影响区域入口的确定.

表1 聚类中心点到两个水源点的最短路径长度
5.3分区边界优化模型
初步分区及分区入口确定后,运用模拟退火算法对分区边界进行优化,优化变量为管网中所有节点的类归属;适应度函数为划分的17个区域之间所有边界管段的流量之和;约束条件为优化过程中必须保持每个区域内所有节点相互连通.最大迭代代数设置为300,终止条件设置为连续20代不接受新解则终止迭代.模拟退火算法迭代过程中适应度函数终值总流量为42.94 L/s.最优解中各区域间管段连接数如表2所示.
5.4分区合并
分区优化边界确定后,此时若将所有区域间连接管段均关闭,还是会导致水力条件无法满足供水要求,因此,需要结合人工经验对分区进行适当合并.此时会有部分区域的节点完全分布在主干管上,这种分布在主干管上的区域无法进行压力控制,不作PMA分区处理.
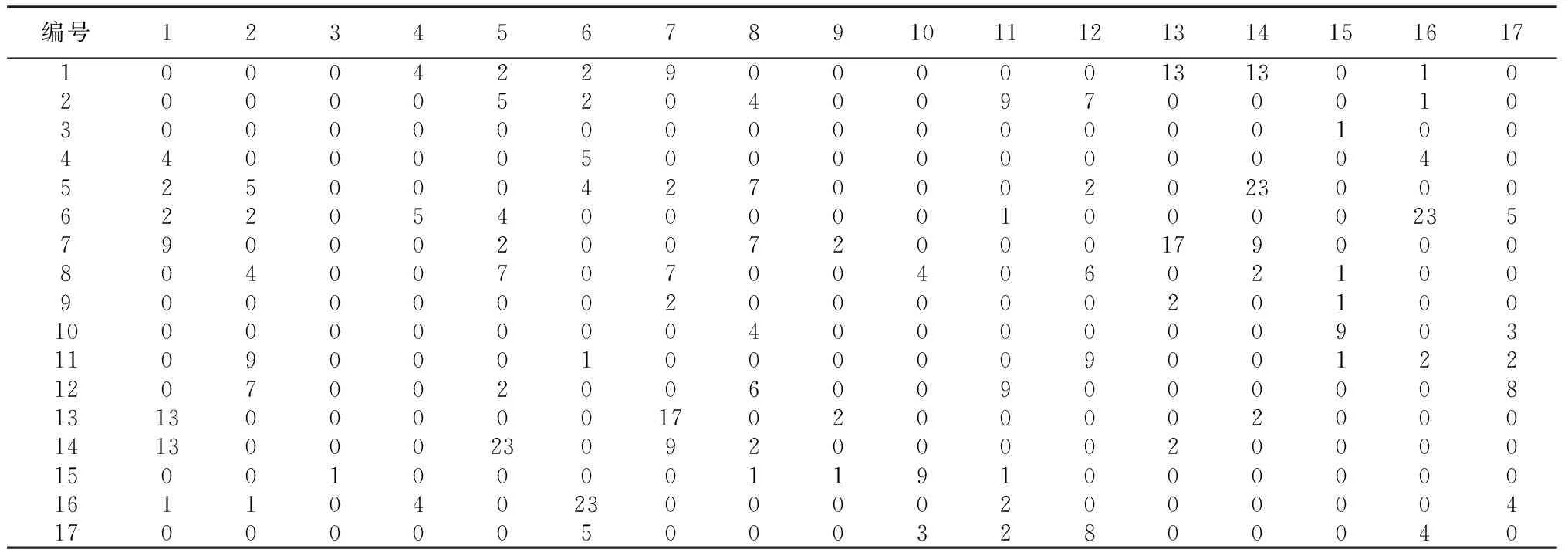
表2 区域间连接管段数量
由表2可以看出,6和16、5和14、1和13、1和14、7和13 这几个分区之间管段连接数较多.最短路径结构以及聚类中心点类编号如图8所示,可以看出,这些管段连接数较多的区域在空间拓扑结构也通常是邻近区域,可以进行合并.2和12分区分布在同一条主干管上,应首先进行合并区域,17节点数过少,不适合单独形成分区,2、12分区管段连接数为8条管段,因此,2、12、17分区合并为一个区域;管段相互连接较多应该一起合并的有1、5、7、13、14这5个分区,分区4在这5个分区供水后端,因此,将1、4、5、7、13、14合并为一个分区;6和16由于连接管段数过多,若完全关断这些管段会导致供水压力不足,将这两个区域进行合并,合并后该区域通过两条主管线供水,若有压力富裕,可在两条管线上均安装压力控制设备;分区9和15的大部分节点均分布在主干管上,并且靠近水源,这两个区域无法单独进行压力控制,因此,不作分区处理.分区完全合并后,共形成7个PMA分区.最终分区结果如图9所示.
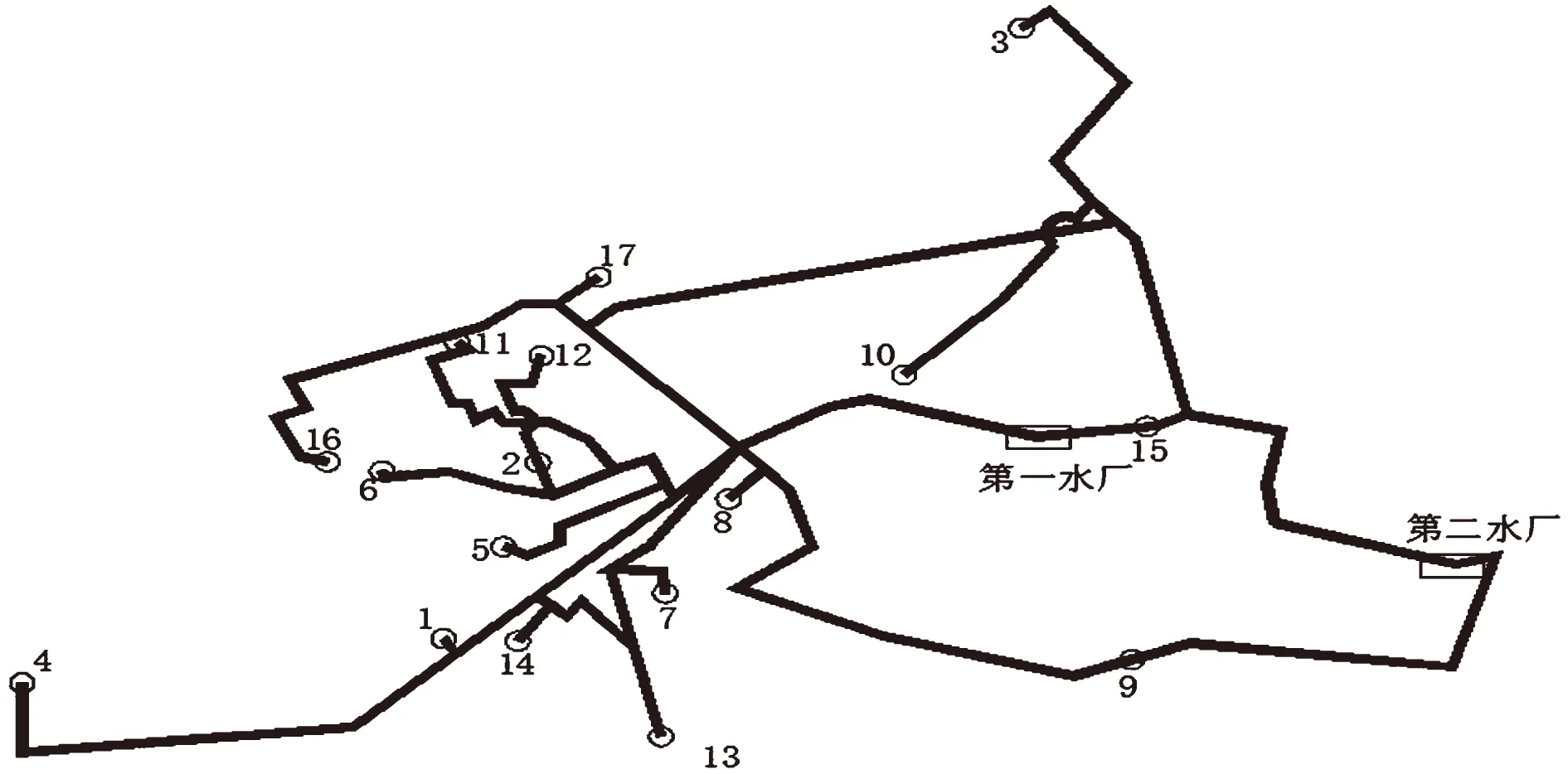
图8 最短路径拓扑结构
5.5分区结果分析
分区完成后,将区域之间的连接管段关闭后得到供水管网日用水量最高时和最低时供水管网自由水头分布,如图10、11所示.比较图10、11和图4、5可以看出,供水管网进行分区后,用水量最低时和最高时的自由水头均呈一定程度下降.此时对各个分区的压力统计结果如表3所示.可以看出,7个分区的压力归一化方差均小于0.4,符合要求.Y市供水管网要求的自由水头值必须大于20 m,从表3可以看出,分区形成后满足供水要求.所以,该分区策略可用于指导实际供水管网PMA分区,并能够取得良好漏失控制效果.

图9 最终分区结果

图10 分区后用水量最高时自由水头分布
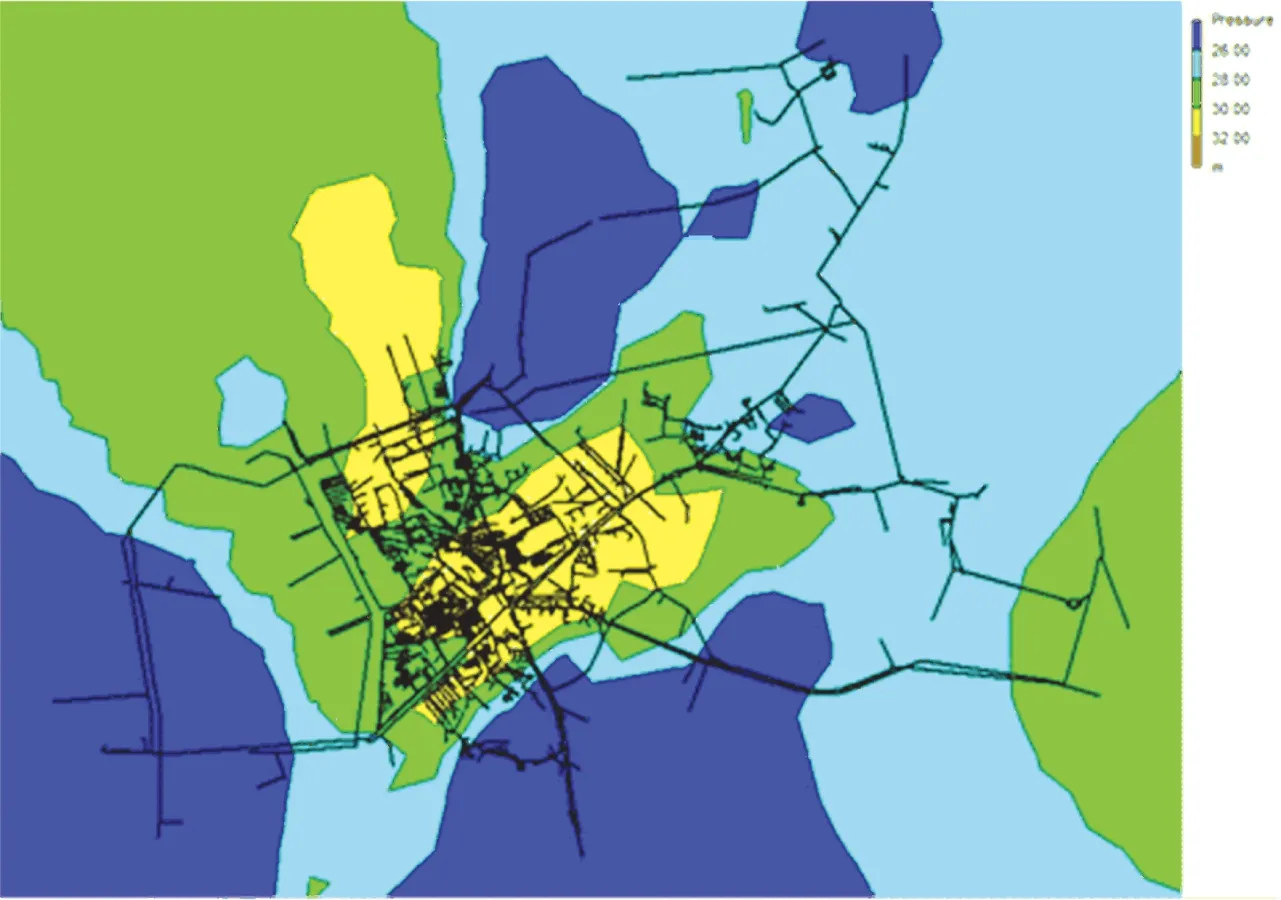
图11 分区后用水量最低时自由水头分布

分区编号压力均值/m压力归一化方差最小自由水头/m125.820.2622.90227.900.3823.55325.120.3521.96426.910.1723.16526.630.2122.97626.090.3322.49726.270.2922.80
6结论
1)结合图论提出一种结合工程实践的自动PMA分区方法,首次将供水管网PMA分区总结为3个方面,即分区数目、分区入口和分区边界.并运用相应算法解决这3个问题,形成最终的可行方案.
2)现有的关于供水管网分区研究通常都是指定分区数目后再分区[20],但对分区数目不能给出合理解释.本文首次将经济计算引入到分区数目的确定中,提出了分区数目确定的合理化方法,提供了一种新的计算思路,具有很强的工程实用价值.
3)分区边界形成后,结合人工经验进行分区合并来保证供水安全性,分区合并的原则是尽可能地保留分区,对水力条件无法满足或供水路径冲突无法形成PMA分区的部分进行分区合并.
参考文献
[1] DI NARDO A, DI NATALE M, MUSMARRA D, et al. A district sectorization for water network protection from intentional contamination[J]. Procedia Engineering, 2014,70:515-524.
[2] DI NARDO A, DI NATALE M, SANTONASTASO G F, et al. Divide and conquer partitioning techniques for smart water networks[J]. Procedia Engineering, 2014,89:1176-1183.
[3] DE PAOLA F, FONTANA N, GALDIERO E, et al. Optimaldesign of district metered areas in water distribution networks[J]. Procedia Engineering, 2014,70:449-457.
[4] MAMADE A, LOUREIRO D, COVAS D, et al. Spatial andtemporal forecasting of water consumption at the DMA level using extensive measurements[J]. Procedia Engineering, 2014,70:1063-1073.
[5] MAY J. Pressuredepend leakage[J]. World Water Environment Engineering,1994(10):15-19.
[6] GODWIN S J. The results of the experimental program on leakage and leakage control[J]. Water Research Center,1980(56):52-154.[7] STERING A. Leakagereduction by optimized control of valves in water networks[J]. Trans Inst MC, 1984,127(13):67-68.
[8] 崔建国,于庆江,梁海荣. 城市给水系统优化调度中的管网分区方法[J]. 太原理工大学学报,2004,5(35):605-608.
CUI J G, YU Q J, LIANG H R. Study on the method dividing districts of water distribution network in optimal dispatch of city water system[J]. Journal of Taituan University of Technology,2004,35(5):605-608.
[9] 周玉文,刁克功,吴珊,等. 城市供水管网分区初步研究[C]//供水管网信息化管理与检测技术应用研讨会论文集. 北京:中国建筑工业出版社,2005:213-221.
ZHOU Y W, DIAO K G, WU S, et al. Preliminary study of urban water supply network partition[C]//Civil Engineering Society of China.Collected Papers on Application of Information Management and Detection Technology System for Water Supply Network Rap Session. Beijing:China Building Industry Press,2005:213-221.
[10]张世泽,袁一星,李玉华. 城市供水管网优化设计两步法[J]. 哈尔滨工业大学学报, 2009, 41(4):111-117.
ZHANG S Z, YUAN Y X, LI Y H. Two-step method for optimal design of water distribution system[J]. Journal of Harbin Institute of Technology, 2009, 41(4):111-117.
[11]董深,吕谋,盛泽斌,等. 基于遗传算法的供水管网反问题流失定位[J]. 哈尔滨工业大学学报,2013, 45(2):106-128.
DONG S, LU M, SHENG Z B, et al. Inverse transient leakage location of water supply network based on genetic algorithm[J]. Journal of Harbin Institute of Technology,2013, 45(2):106-128.
[12]MOUNCE S R,BOXALL J B,MACHELL J. Development and verification of an online artificial intelligence system for detection of bursts and other abnormal flows [J]. Journal of Water Resources Planning and Management, 2010, 136(3):309-318.
[13]FERY B J,DUDCK D. Clustering by passing messages between data points[J].Science,2007,315 (5814):972-976.
[14]郭秀娟,陈莹. AP聚类算法的分析与应用[J]. 吉林建筑大学学报, 2013,30(4):58-61.
GUO X J, CHEN Y. Analysis and application on AP clustering algorithm[J]. Journal of Jilin Jianzhu University, 2013,30(4):58-61.
[15]何晏成. 基于近邻传播和凝聚层次的文本聚类方法[D]. 哈尔滨:哈尔滨工业大学, 2010:60.
HE Y C. A document clustering method based on affinity propagation and agglomerative hierarchical clustering[D].Harbin: Harbin Institute of Technology,2010:60.
[16]张念. 用Dijkstra算法实现对整车配送线路的优化[J]. 中国水运(理论版), 2007,5(5):141-142.
ZHANG N. Implement the optimization of vehicle distribution line based on Dijkstra algorithm[J]. China Water Transport, 2007,5(5):141-142.
[17]杨蔓. 最短路径算法在煤矿安全分区分析中的应用研究[D]. 西安:西安科技大学, 2009:77.
YANG M. The study on the analysis of shortest path algorithm in the coal mine safety subarea[D]. Xi’an: Xi’an University of Science and Technology,2009:77.
[18]CARSTEN D. Optical design of multilayer achromatic waveplate by simulated annealing algorithm[J]. Chinese Journal of Astronomy and Astrophysics, 2008(3):349-361.
[19]张红娟. 基于非格点模型的蛋白质结构预测研究[D]. 大连:大连理工大学, 2006:55.
ZHANG H J. The research on the protein structure prediction based on the off-lattice protein model[D]. Danlian: Danlian University of Technology,2006:55.
[20]何忠华,袁一星. 基于分区模型的城市供水管网压力监测点布置[J]. 哈尔滨工业大学学报,2014,46(10):37-41.
HE Z H, YUAN Y X. Layout of pressure monitoring points in urban water distribution system based on district model[J].Journal of Harbin Institute of Technology,2014,46(10):37-41.
(编辑刘彤)
doi:10.11918/j.issn.0367-6234.2016.08.011
收稿日期:2015-11-07
基金项目:国家自然科学基金(51278148);国家水体污染控制与治理科技重大专项(2014ZX07405002);广东省教育部产学研结合项目(2011A090200040)
作者简介:高金良(1971—),男,副教授,硕士生导师
通信作者:姚芳,yaofang0525@163.com
中图分类号:TU991
文献标志码:A
文章编号:0367-6234(2016)08-0067-06
Optimization of water supply network PMA partition by graph theory
GAO Jinliang, YAO Fang, YE Jian
(School of Municipal and Environmental Engineering,Harbin Institute of Technology, Harbin 150090, China)
Abstract:The water supply pipe network pressure management area (PMA) partition, which is pressure-control oriented and regional metrology considered, effectively controls the leakage rate of urban water supply network. PMA partition with graph theory is proposed in this study. First of all, to initially partition the water supply network and set the partition number with adaptive AP clustering algorithm and economic calculation. Secondly, Dijkstra algorithm is adopted to calculate the shortest path of each cluster center point to the source of the water and determine the position of each division of the water supply pipe, and then establish a partition boundary optimization model and apply simulated annealing algorithm to solve the model. Finally, combine some partitions properly with artificial expertise and form the final plan. This partition, computer algorithm oriented and combined with artificial expertise, embraces larger search space than the traditional artificial partition of trial and error and can guide the actual water supply network PMA partition.
Keywords:PMA partition; graph theory; AP clustering algorithm; Dijkstra algorithm; simulated annealing algorithm
