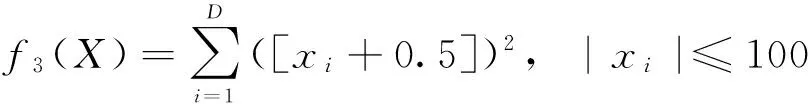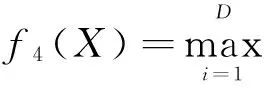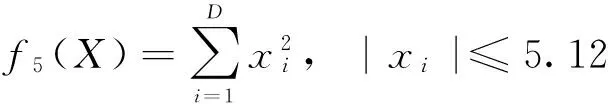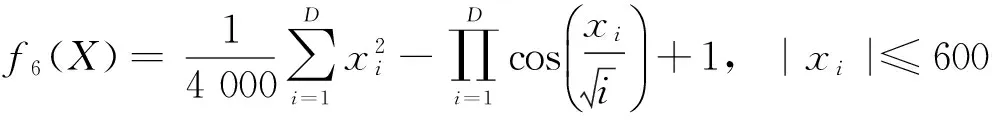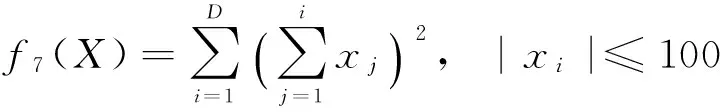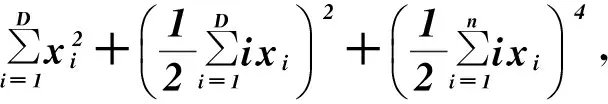采用多搜索模式的粒子群算法

张呈志, 王　勇, 李海滨

(广西民族大学 a.信息科学与工程学院;b.广西高校复杂系统与智能计算重点实验室，南宁　530006)



采用多搜索模式的粒子群算法

张呈志, 王勇, 李海滨

(广西民族大学 a.信息科学与工程学院;b.广西高校复杂系统与智能计算重点实验室，南宁530006)

摘要：从现实中鸟的搜索方式中得到灵感, 提出一种新的变异粒子群算法, 称之为采用多搜索模式的粒子群优化算法(MMPSO)。该算法中的每个粒子使用3种搜索模式在搜索空间中搜索食物, 可随时调整其搜索方式。在数值仿真实验中选择了几个比较典型的高维复杂优化问题用来测试算法的性能。结果表明:算法的全局搜索能力和避免粒子陷入局部最优的能力都得到了明显提高, 在一定程度上避免了早收敛现象的发生, 可用于求解高维复杂函数的优化问题。

关键词：粒子群算法;多搜索模式;MMPSO

0引言

粒子群优化算法(particle swarm optimization, PSO)[1]是Kennedy和Eberhart于1995年共同提出的一种基于群体智能的并行优化算法。由于PSO算法具有理论方法简单、设置参数少、易于编码实现等特点, 且在复杂优化问题、工程等方面也得到了广泛应用, 因而自PSO算法提出以来, 越来越受到学者们的关注；但与其他随机搜索算法相似, PSO算法也存在早熟收敛的不足。 针对标准PSO存在的不足, 不少学者对PSO开展了较为深入的研究, 提出了多种PSO改进策略[2-30], 取得了不少研究成果。例如： 吕振肃等[8]提出一种基于群体适应度方差自适应变异的粒子群优化算法(AMPSO); 赫然等[9]提出一种改进的自适应逃逸微粒群算法; Liang等[16]提出一种全面学习的粒子群优化算法(CLPSO); 吕强等[17]将蚁群优化算法的信息素共享机制引入到粒子群优化算法中, 提出一种基于信息素机制的粒子群优化算法(PSO-PM)， 以及一种信息充分交流的粒子群优化算法(PSO-FCI)[18]; 吴晓军等[19]提出一种均匀搜索粒子群算法(UPSO); 魏波等[20]提出基于稳定策略的粒子群优化算法(SSPSO); 高哲等[22]提出一种基于平均速度的混合自适应粒子群算法; 杜继永等[23]提出一种具有初始化功能的自适应惯性权重粒子群算法(IAW-PSO); 喻飞等[24]提出一种去个性化理论的粒子群算法(DTPSO); 朱庆保等[25]提出一种求解动态连续优化的分层粒子群算法(LDPSO); 文献[26-27]提出了将差分进化与PSO相结合的混合优化方法; 文献[28-29]提出了将遗传算法(GA)与PSO相结合的混合优化方法; 文献[30]提出了将蚁群算法(ACO)与PSO相结合的混合优化方法等等。

以上改进策略归纳起来主要有:1)控制惯性权重、学习因子、飞行速度等参数, 以平衡算法的全局搜索与局部搜索能力;2)引入一些使算法能跳出局部极值的机制;3)将群体划分成若干个子群、定义不同的邻域拓扑结构, 以使种群的多样性得到保持;4)完全沿用标准PSO设计粒子的飞行模式， 规定粒子只能飞到介于当前群体最优与个体历史最优的某一小范围内觅食, 粒子只采用不变向飞行方式。尽管文献[2-30]提出的方法在一定程度上改善了PSO的优化性能, 但在应用于求解维数较高的复杂优化问题时, 仍出现早熟收敛问题。考虑到标准PSO是从鸟的觅食行为特征中得到灵感而提出的，本文也从现实鸟的飞行方式和觅食行为方式中寻找答案, 提出一种新的变异粒子群算法, 即一种采用多搜索模式的粒子群算法(particle swarm optimization by using multi-search modes, MMPSO), 并通过数值仿真实验对算法性能进行了验证。

1标准粒子群算法存在的不足

设t时刻第i粒子在搜索空间中的位置和飞行速度分别表示为Xi(t)=(xi1(t),xi2(t), …, xiD(t))和Vi(t)=(vi1(t),vi2(t), …,viD(t)), 第i粒子经历过的最优位置记为Pbest(t)=(pi1(t),pi2(t), …, piD(t));所有粒子当前找到的最优位置记为Gbest(t)=(g1(t),g2(t), …, gD(t))。第i粒子则按下式来更新其飞行速度和位置:

vid(t+1)=wvid(t)+c1r1(pid(t)-xid(t))+

c2r2(gid(t)-xid(t)),

(1)

xid(t+1)=xid(t)+vid(t+1),d=1, 2， …,D。

(2)其中:w为惯性权重因子;c1和c2为正的加速常数;r1和r2为[0,1]内的均匀随机数;D为搜索空间维数。式(1)由3部分组成:第1部分wvid(t)为“惯性(inertia)”, 代表粒子有维持自己先前速度的趋势;第2部分c1r1(pid(t)-xid(t))为“认知(cognition)”部分, 反映了粒子对自身历史经验的记忆或回忆, 代表粒子有向自身历史最佳位置逼近的趋势;第3部分c2r2(gid(t)-xid(t))为“社会(social)”部分,反映了粒子间协同合作与知识共享的群体历史经验, 代表粒子有向群体或邻域历史最佳位置逼近的趋势。

分析标准PSO算法中的粒子飞行控制式(1)和式(2), 可知粒子的飞行方式(搜索方式)有以下约束: 1)粒子被限制在由个体当前位置、 个体历史最优位置与群体当前最优位置所构成的扇形区域内开展搜索活动, 由于被个体历史最优位置与群体当前最优位置吸引， 粒子终将聚集到群体当前最优位置的附近, 从而使粒子群过早聚集到群体当前最优位置的附近, 使种群的多样性得不到有效的保持, 导致算法搜索丧失了跳出局部最优的能力;2)群体中所有粒子任何时候都只能以式(1)和式(2)来控制其飞行(搜索)方式。这一约束条件在很大程度上使粒子的飞行(搜索)活动缺乏机动性和灵活性, 降低了粒子躲避障碍物或天敌的能力(即跳出局部最优的能力)，同时也降低了粒子的搜索能力, 最终降低了粒子跳出局部最优的能力。

2采用多搜索模式的粒子群算法

2.1算法基本思想

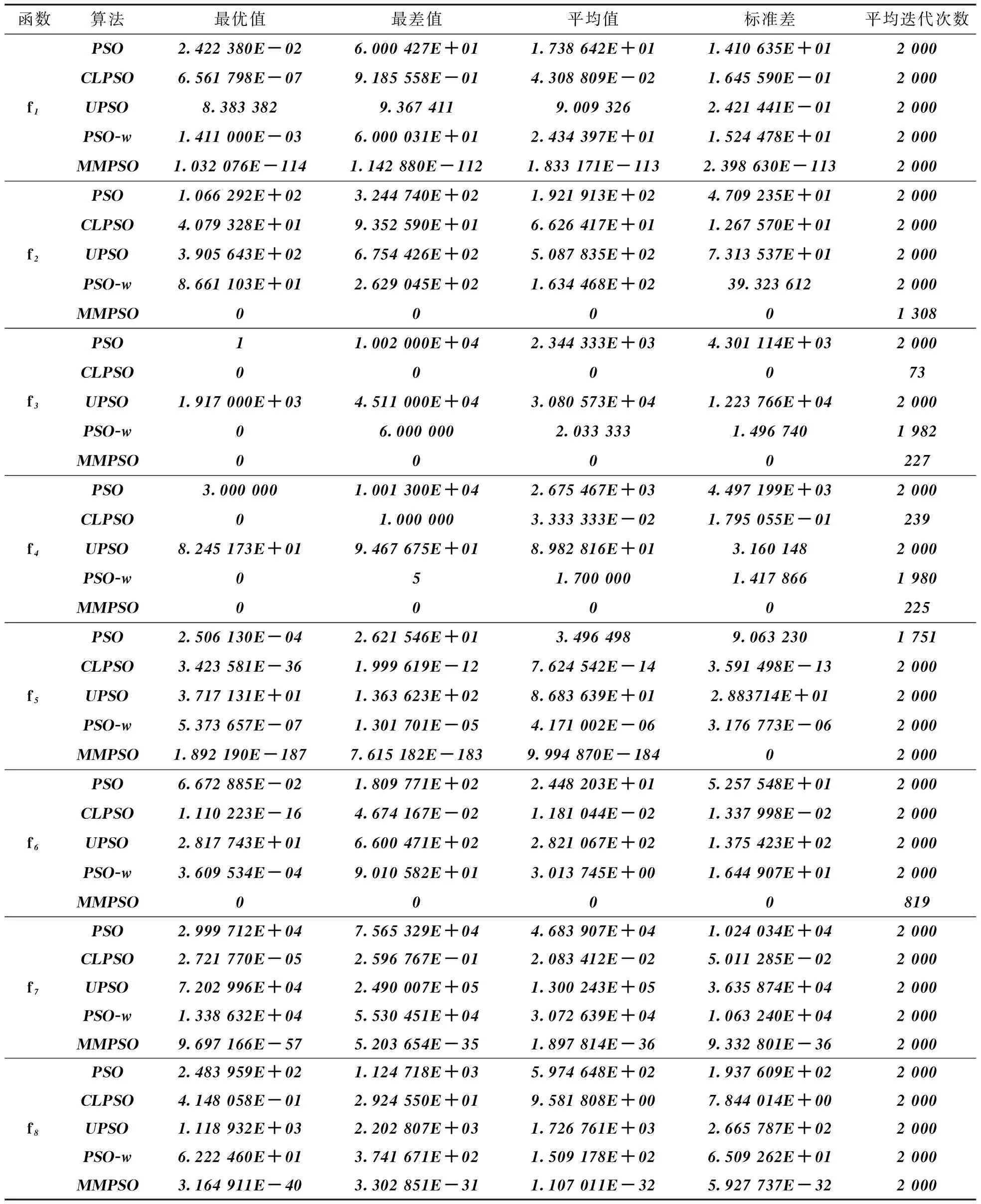
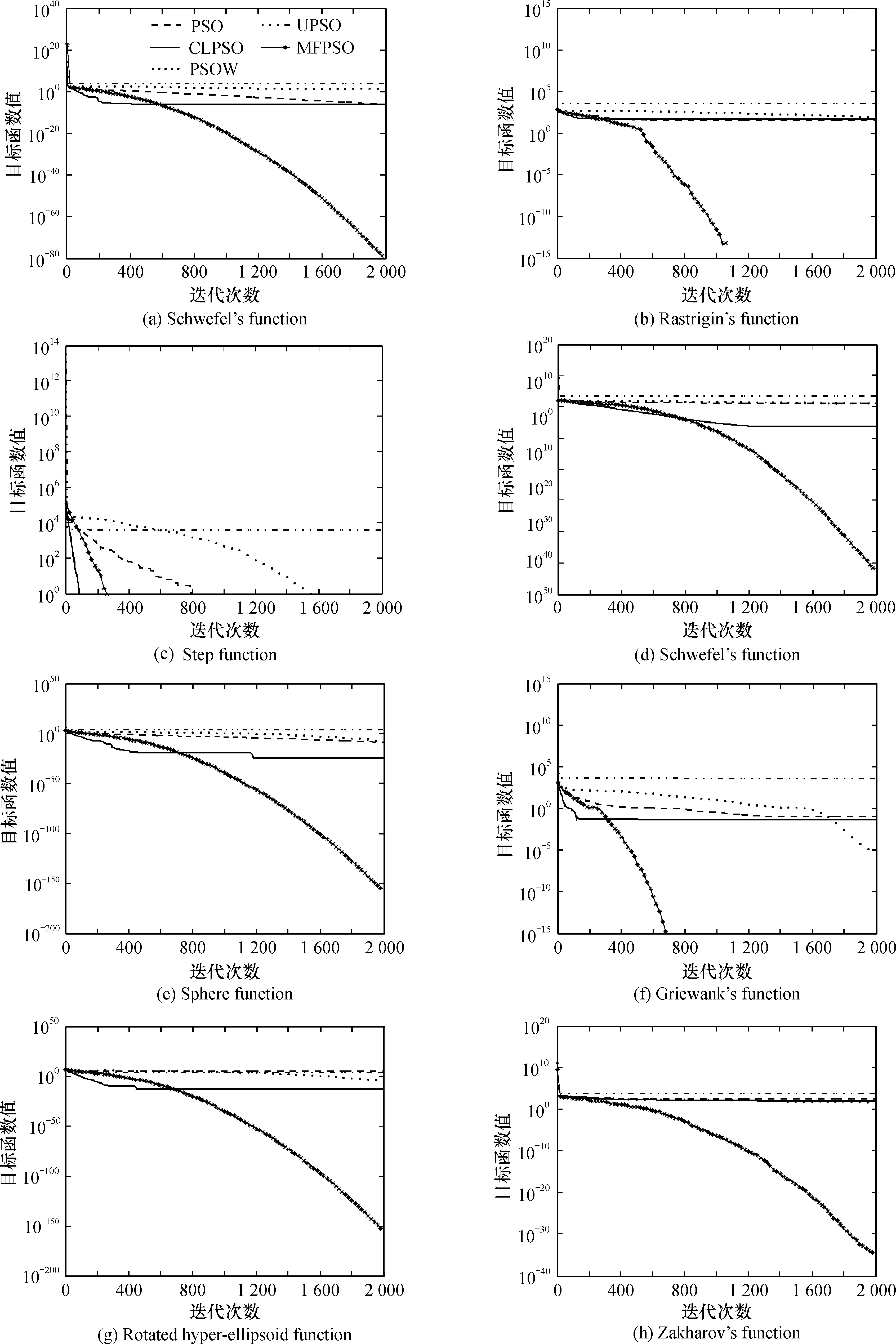
自然界中的鸟通常有以下特点:1)具有较好的飞行技能和较强的搜索食物的能力, 在飞行过程中可随时调整飞行速度、改变飞行方向、 可视不同情况调整飞行模式。如鸟在觅食过程中, 可绕过障碍物、躲避天敌的攻击, 可采用灵活多变的飞行方式在丛林里搜寻食物。2)鸟与鸟之间是通过鸣叫声向对方传递信息的。然而在同一时刻, 鸟群中有些鸟可能听到其他鸟的鸣叫声(即接收到信息), 有些则可能没有听到(即没有接收到信息)。某一个体能否接收到另一个体发出的信息, 通常与其当时所处的位置有关。所处的位置越好, 接收到信息的概率就越大;反之则越小。3)鸟在树林里的搜索果实活动, 大体上可分为3种情况:一是个体在搜索空间中开展自由搜索活动;二是有多个个体参与和配合的集体搜索活动;三是有多个个体发现某棵树上有果实后, 就飞到那棵树上开展搜索果实的活动。

根据以上鸟的搜索(飞行)活动特征, 规定鸟在觅食活动中, 只有以上所提及的3种情况。相应地, 规定鸟(粒子)的搜索(飞行)模式只有3种:漫游模式、 搜索模式、 觅食模式。

2.2算法描述

基于以上基本思想, 对粒子(鸟)的搜索模式作如下改进:

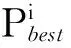
(3)

则称其在t时刻按个体搜索模式开展搜索活动。其中c为d中的随机数,d=1,2, …,D。该粒子的搜索方向如图1所示。

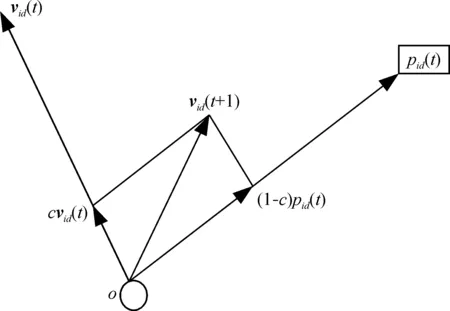
图1　粒子搜索方向示意图Fig.1　Sketch map of particle searching direction

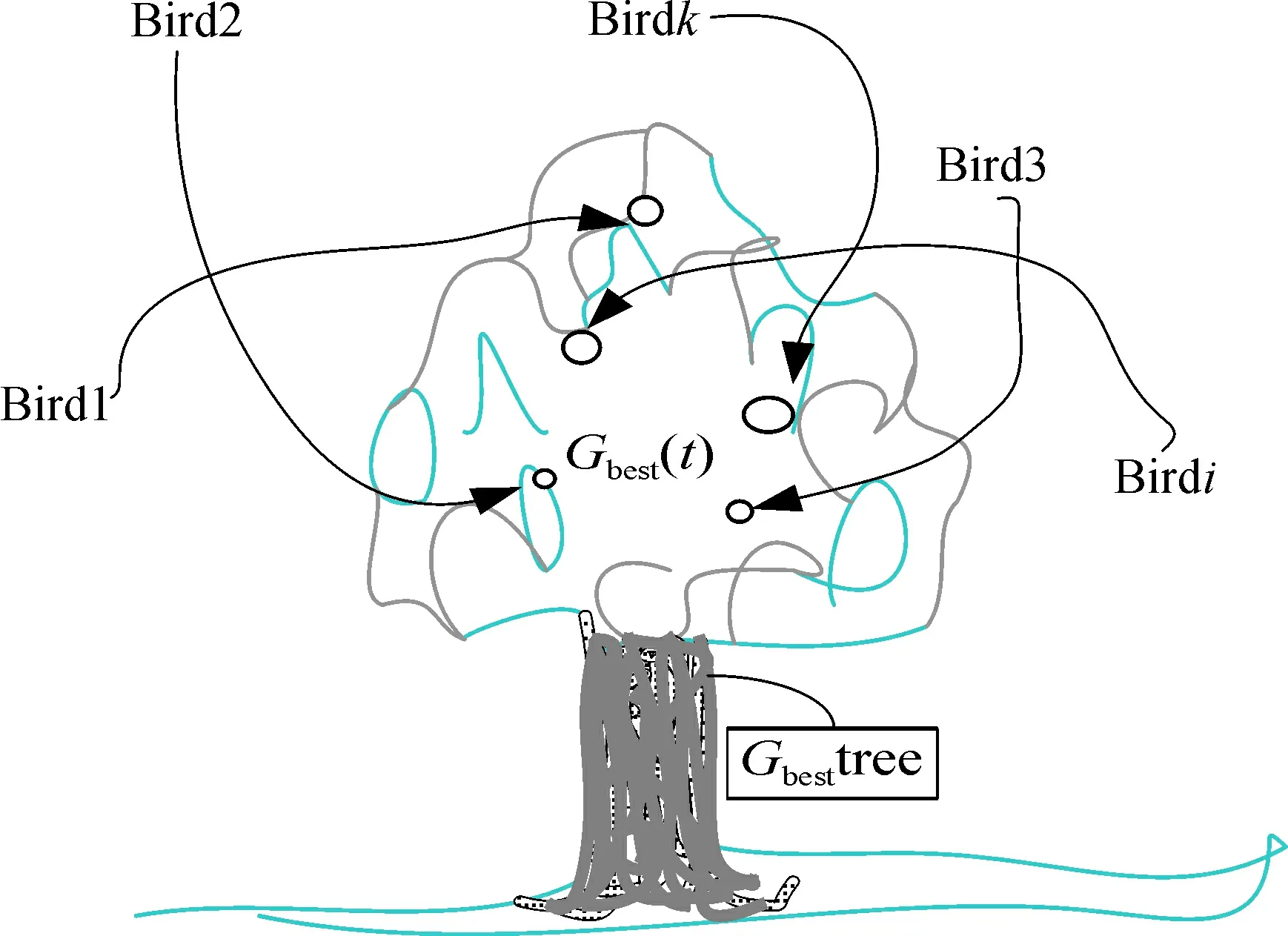
② 搜索模式。若第i粒子(鸟)在t时刻开展搜索活动:

(4)

则称其在t时刻按集体搜索模式开展搜索活动。其中w(t)为关于时间t的递减函数, 0

③ 觅食模式。若第i粒子(鸟)在t时刻飞到Gbest(t)的周围开展觅食行动:

xid(t+1)=gk(t),d=1,2, …,D。

(5)

其中,k为{1, 2,…,D}中的一个随机数, 则称其在t时刻按集体觅食模式开展搜索活动。鸟群从不同的方向飞到目标Gbest(t)附近的情景如图2所示。

这说明， 粒子(鸟)发现目标Gbest之后, 并不是直接飞到点Gbest处觅食, 而是从不同的方向， 采用变向的飞行方式飞到点Gbest的周围寻找食物, 或者在Gbest的周围开展觅食活动, 而直接飞向点Gbest觅食的粒子(鸟)则非常少。

2.3飞行模式选择方法

由于鸟是通过鸣叫向群体中的其他个体传递信息的, 而对方能否接收到信息, 与其当时所处相对位置的优劣有关。因此, 首先确定信息发布规则，规定当前位置最优者为信息发布者;其次, 设计信息接收规则，粒子(鸟)接收到信息的概率, 与其所处的位置优劣有关;再次, 设计粒子(鸟)的搜索模式选择规则，粒子(鸟)视不同的情况选择不同的搜索模式。

图2　鸟飞到目标树上觅食示意图Fig.2　Schematic diagram of birds flying to the object tree to forage

根据以上描述, 假定个体利用群体信息来选择其飞行模式的方法:设群体规模为M, 第i粒子t时刻位于Xi(t)。首先将群体依据适应度从最优到最差进行排序, 记第i粒子t时刻在群体中排第si(t)位, 则1≤si(t)≤M。若si(t)=1, 则表示第i粒子t时刻为群体当中位置最优者；si(t)=M, 则表示第i粒子t时刻为群体当中最差者, 定义

(6)

为位于Xi(t)的第i粒子(在t时刻)可接收到信息发布者(位于Gbest(t))发出声音强度的最小值。显然0≤si(t)≤1。此时, 若第k粒子的位置是X1(t),X2(t), …,XM(t)当中最优者, 则sk(t)≤sj(t);若第k粒子的位置是最差者, 则sj(t)≤sk(t)=1,j=1, 2,…,M。也就是说,si(t)越小, 表示位于Xi(t)的第i粒子接收到信息发布者(位于Gbest(t))发出声音信号的概率也就越大。

记φ(t)为信息发布者在t时刻发出的声音强度值, 其中φ(t)为(0, 1]中的均匀随机分布。作以下规定:

(i)若φ(t)

综上所述, 粒子的搜索模式选择规则如下:假定信息发布者在t时刻发布信息的声音强度值是φ(t), 则第i粒子按如下式来调整其搜索模式:

(7)

其中,φ(t)为(0, 1]中的均匀随机分布, 是信息发布者在t时刻的鸣叫声(信号)强度值。

3实验仿真与结果分析

为了验证本文算法(MMPSO)的性能, 选取比较具有代表性的PSO-w[3]、 CLPSO[16]、 UPSO[19]、 标准PSO与本文算法(MMPSO)进行算法性能比较。 本次实验采用Matlab 2010a进行编程, 在AMD Athlon(tm) x2(2 CUPs) 3.0 GHz, 2 G RAM平台进行测试。

3.1测试函数

在本文的数值实验中, 选用8个比较经典的优化测试基准函数。具体选用的基准测试函数如下(其中搜索空间的维数D=50):

(a)Schwefel’sfunction:

该函数为单峰函数,Schwefel函数在点(0, …, 0)处取得全局唯一极小值是0。

(b)Rastrigin’sfunction:

|xi|≤5.12。

该函数为多峰函数, 它是一个典型的用来测试算法全局搜索性能的函数, 其峰形呈高低起伏不定跳跃性, 在搜索区域内约有10D个局部极小值点, 很难搜索到全局最优值, 该函数在点(0, …, 0)处取得全局极小值是0。

(c)Stepfunction:

该函数为不连续的阶梯函数, 在-100≤xi≤100时, 在点(0, …, 0)取得全局极小值0。

(d)Schwefel’sfunction:

该函数为单峰函数, 在点(0, …, 0)处取得全局极小值是0。

(e)Spherefunction:

该函数为单峰函数, 在点(0, …, 0)处取得全局极小值是0。

(f)Griewank’sfunction:

(g)Rotatedhyper-ellipsoidfunction:

该函数是一个单峰函数, 它在点(0, …, 0)处取得全局唯一最小值是0。

(h)Zakharov’sfunction:

-5≤xi≤10。

该函数为单模函数, 它在点(0, …, 0)处取得全局极小值是0。

3.2实验仿真

为了具有可比性, 在算法数值实验中, 使5种算法的参数设置尽可能保持一致, 其具体参数设置如下:种群规模都设为30, 加速常数设置为c1=c2=2, 最大迭代次数设置为G=2 000。对于标准PSO、 CLPSO及UPSO 3种算法, 设置w(t)=0.628, 对于PSO-w算法, 则w从0.9线性下降到0.4， 并限定粒子的最大速度vmax≤20%(bj-aj), 其中aj和bj分别为第j维搜索域的下界和上界， 对于本文算法(MMPSO)， 取w(t)=0.9-(0.9-0.4)t/T。

实验仿真中, 设置算法运行停止条件: 若算法搜索到精确解, 或者算法运行达到最大迭代次数时, 算法停止运行。为了避免随机性对实验结果的影响, 每一种算法对每个优化问题均独立运行30次。记录最优值、 最差值、 平均值、 标准差、 平均迭代次数等评价指标的实验数据。 这些评价指标总体上反映了算法的优化能力, 同时也反映了算法计算代价的高低。 表1列出了5种算法独立运行30次所得到的实验数据。

对比这5种算法的收敛速度, 5种算法各自独立运行30次所得到的目标函数最优值(适应度)的平均值的收敛曲线仿真图3, 图3a—h为上述5种算法分别对8种优化测试基准函数各自独立运行30次所得到的目标最优值(适应度)的平均值收敛曲线仿真图。

表1　实验结果Table 1　Experiment results

图3　50维测试函数平均收敛仿真图Fig.3　Median convergence simulation diagrams of 50D test functions

3.3对比分析

从实验结果(表1、图3)可以看出:本文算法(MFPSO)在测试函数f1、f2、f3、f4、f5、f6、f7、f8这8个基准函数的优化问题上, 总体上都具有比标准PSO、PSO-w、CLPSO、UPSO这4种算法更快的全局收敛速度和更好的优化精度;从“标准差”这一评价指标上看, 本文算法(MMPSO)的稳定性比上述4种算法都要好;从“平均迭代次数”评价指标以及仿真图3上看, 本文算法的收敛速度总体上比上述4种算法都要快。

综上所述, 本文提出的MFPSO算法改善了PSO算法的优化性能, 与标准PSO、CLPSO、PSO-w以及UPSO 4种算法相比, 其优化性能得到了较大的改善, 在很大程度上克服了标准PSO易陷入局部最优之不足, 在一定程度上避免了PSO算法的早熟收敛现象的出现。

4结束语

针对标准PSO存在的早熟收敛现象, 本文通过增加粒子的搜索模式来增强粒子跳出局部最优的能力和提高粒子的搜索效率。本文选取了8个比较典型的基准函数, 用以测试本文算法(MMPSO)以及标准PSO、CLPSO、PSO-w、UPSO的优化性能。结果表明:本文算法(MMPSO)具有比标准PSO、PSO-w、CLPSO和UPSO 4种算法更快的全局收敛速度、更强的跳出局部最优的能力、更好的全局优化能力和更好的稳定性。

参考文献:

[1]Kennedy J, Eberhart R. Particle swarm optimization[C]//Proc.of the IEEE International Conference on Neural Networks 1995,IEEE Press,1995:1942-1948.

[2]Shi Y H, Eberhart R. A modified particle swarm optimizer[C]//Procedings of IEEE International Conference on Evolutionary Computation. Piscataway, NJ, USA:IEEE Press, 1998:69-73.

[3]van den Bergh F, Engelbrecht A P. A cooperative approach to particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 225-239.

[4]Løpvbjerg M, Rasmussen T K, Krink T. Hybrid particle swarm optimiser with breeding and subpopulations[C]//Proc.Genetic Evol.Comput.Conf., 2001:469-476.

[5]Kennedy J, Mendaes R. Neighborhood topoligies in fully-informed and best-of-neighborhood particle swarms[J].IEEE Transactions on Systems, Man, and Cybernetics, Part C:Application and Reviews, 2006, 36(4):515-519.

[6]Kennedy J, Mendes R. Population structure and particle swarm performance[C]//Proc. of the IEEE Congress on Evolutionary Computation. Honolulu, USA, 2002:1671-1676.

[7]Liang J J,Suganthan P N. Dynamic multi-swarm particle swarm optimizer[C]//Proc. of IEEE Int. Swarm Intelligence Symposium, 2005:124-129.

[8]吕振肃, 侯志荣. 自适应变异的粒子群优化算法[J].电子学报, 2004, 32(3):416-420.

[9]赫然, 王永吉, 王青,等.一种改进的自适应逃逸微粒群算法及实验分析[J].软件学报, 2005, 16(12):2036-2044.

[10]陈红洲, 顾国昌, 康望星. 一种具有感觉的微粒群算法[J]. 计算机研究与发展, 2005, 42(8):1299-1305.

[11]吕艳萍, 李绍滋, 陈水利, 等. 自适应扩散混合变异机制微粒群算法[J]. 软件学报, 2007, 18(11): 2740-2751.

[12]王辉, 钱峰. 基于惯性权重非线性动态变化的微粒群算法[J]. 计算机科学, 2008, 35(3):146-148.

[13]Jiao B, Lian Z G,Gu X S. A dynamic inertia weight particle swarm optimization algorithm[J].Chaos,Solitons and Fractals,2008, 37(3): 698-705

[14]Ratnaweera A, Halgamuge S K,Watson H C.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients[J]. IEEE Transactions on Evolutionary Computation,2004, 8 (3): 240-255.

[15]丛琳, 沙宇恒, 焦李成.组织进化粒子群数值优化算法[J].模式识别与人工智能, 2007, 20(2):145-153.

[16]Liang J J,Qin A K,Suganthan P N, et al. Comprehensive learning particle swarm optimizers for global optimization of multimodal functions[J].IEEE Transactions on Evolutionary Computation, 2006, 10(3):67-82.

[17]吕强, 刘士荣, 邱雪娜.基于信息素机制的粒子群优化算法的设计与实现[J].自动化学报, 2009, 35(11):1410-1419.

[18]吕强, 刘士荣. 一种信息充分交流的粒子群优化算法[J]. 电子学报, 2010, 38(3):664-667.

[19]吴晓军, 杨战中, 赵明. 均匀搜索粒子群算法[J].电子学报, 2011, 39(6):1261-1266.

[20]魏波, 李元香, 徐星, 等. 基于稳定策略的粒子群优化算法[J].计算机科学, 2011, 38(12):221-223.

[21]董方, 谢磊, 张建明. 基于反馈学习粒子群算法的极值搜索控制[J].上海交通大学学报, 2012, 46(12): 1962-1966.

[22]高哲, 廖晓钟. 基于平均速度的混合自适应粒子群算法[J].控制与决策, 2012, 27(1):152-155，160.

[23]杜继永, 张凤鸣, 李建文, 等. 一种具有初始化功能的自适应惯性权重粒子群算法[J]. 信息与控制, 2012, 41(2):165-169.

[24]喻飞, 李元香, 魏波, 等. 一种基于去个性化理论的粒子群算法[J]. 控制与决策, 2013, 28(10):1520-1524.

[25]朱庆保, 徐晓晴, 朱世娟. 一种新的求解动态连续优化的分层粒子群算法[J]. 控制与决策, 2013, 28(10):1573-1577.

[26]Zhang W J, Xie X F. DEPSO: Hybrid particle swarm with differential evolution operator[C]//IEEE International Conference on System, Man and Cybernetics, 2003:3816-3821.

[27]栾丽君, 谭立静, 牛奔.一种基于粒子群优化算法和差分进化算法的新型混合全局优化算法[J].信息与控制, 2007, 36 (6):708-714.

[28]彭晓波, 桂卫华, 黄志武, 等. GAPSO:一种高效的遗传粒子混合算法及其应用[J].系统仿真学报, 2008, 20(18):5025-5027，5031.

[29]高尚, 韩斌, 吴小俊, 等. 求解旅行商问题的混合粒子群优化算法[J].控制与决策, 2004, 19(11):1286-1289.

[30]刘波, 杨路明, 雷刚跃, 等.融合粒子群与蚁群算法优化XML群体智能搜索[J].计算机研究与发展, 2008, 45(8):1371-1378.

文章编号:1674-9057(2016)02-0402-08

doi:10.3969/j.issn.1674-9057.2016.02.036

收稿日期：2015-02-01

基金项目：广西自然科学基金项目(0832084)；广西高等学校科研项目(KY2015YB078)

作者简介：张呈志(1985—)，男，硕士，研究方向：计算智能。

通讯作者：王勇，教授，博士，wangygxnn@sina.com。

中图分类号：TP18

文献标志码：A

Particle swarm optimization by multi-search modes

ZHANG Cheng-zhi, WANG Yong, LI Hai-bin

(a.College of Information Science and Engineering;b.Key Laboratory of Guangxi High School Complex System and Computational Intelligence, Guangxi University for Nationalities,Nanning 530006,China)

Abstract:From inspiration of real birds search-modes,a novel variant particle swarm optimization was proposed,which is called the particle swarm optimization by multi-search modes. In this MMPSO, each particle can use three search-modes to search food in search space, and can adjust its method at any time. Experiments were done on some benchmark functions such as Schwefel function, Rastrigin function, Step function,Sphere function, Griewank function, Rotated hyper-ellipsoid function, and Zakharov function. The experimental results show that the MMPSO has stronger ability to jump out of local optimum and better ability of global optimization than that of the normal PSO, and effectively avoid the premature convergence problem.It can be used to solve the high-dimensional and complex optimization problems.

Key words:particle swarm optimization (PSO);multi-search modes;MMPSO

引文格式：张呈志, 王勇, 李海滨.采用多搜索模式的粒子群算法[J].桂林理工大学学报，2016,36(2):402-409.