小波分解层数及分量组合对滑坡预测的影响
2016-08-08卢献健晏红波梁月吉
卢献健,晏红波,梁月吉
(桂林理工大学 a.测绘地理信息学院;b.广西空间信息与测绘重点实验室,广西 桂林 541004)
小波分解层数及分量组合对滑坡预测的影响
卢献健,晏红波,梁月吉
(桂林理工大学 a.测绘地理信息学院;b.广西空间信息与测绘重点实验室,广西 桂林541004)
摘要:针对滑坡变形具有非平稳性、非线性与随机性变化特点,提出将小波分解与RBF神经网络相结合应用于滑坡变形预测。通过实验进行小波分解及不同低频-高频分量组合的预测,着重分析了不同的小波分解层数、分量组合形式以及预测步长对滑坡变形预测的影响。实验分析结果表明:只有选取适当的分解层数、合理的低频-高频分量组合与预测步长,才能得到最优的预测效果。同时也验证了本文方法的正确性,对于滑坡变形预测具有一定的参考意义。
关键词:滑坡预测;小波分解;分量组合;RBF神经网络
0引言
边坡位移及失稳是自然边坡与人工边坡经常遇到的变形现象,及时掌握边坡变形发展演化的规律,准确预测边坡变形的未来演化规律与发展趋势,对边坡稳定性评价、边坡安全状态的预警以及滑坡灾害的控制具有重要意义[1]。由于滑坡成因复杂,滑坡变形信号通常表现为典型的非线性、非平稳性及随机性时间序列,传统的预测方法难以得到满意的预测效果。近年来,时间序列模型、神经网络模型及卡尔曼滤波模型在滑坡预测方面得到了成功应用[2-4]。同时,针对变形时间序列的特征提取,基于分解-合成的方法逐渐得到了重视,比如基于经验模态分解或小波分解,再结合神经网络或支持向量机等人工智能算法进行预测,这些组合预测模型取得了较传统方法更优的预测效果[5-8]。李潇等[8]成功将小波分解与支持向量机相结合用于滑坡变形预测,证实了进行多尺度分解再预测合成有利于提高预测精度。虽然基于分解再预测合成的方法具有较好的优势,但是大多数的研究通常仅进行3层小波分解,然后对各分解分量进行建模预测,没有分析小波分解层数与不同分量组合对滑坡变形预测精度的影响;而且,在建模预测的过程中基本采用滚动式的单步递归预测方法,没有合理地分析预测步长的选择对滑坡预测结果的影响。
基于上述问题,本文建立了小波分解-RBF神经网络预测模型,从小波分解层数、分量组合与预测步长三方面出发,着重分析其对滑坡预测精度的影响,意在探索合适的小波分解层数、分量组合与预测步长以使变形预测能达到最佳效果。
1RBF神经网络多步超前预测模型
RBF神经网络[9]是由输入层、隐含层与输出层3层结构组成,其中隐含层主要是完成低维输入量向高维集合的非线性变换,本文选取径向基函数作为隐含层的激励函数。对于滑坡变形序列{x(t),t=1,2,…,n}, n为序列的长度, 网络的输出层为线性层,由隐含层输出线性组合得到


(1)
式中: c为隐层节点的个数; vi与ρi分别为第i个隐层高斯基函数的中心与扩展常数; wi为连接隐层与输出层的权值。


(2)
2基于小波分解的滑坡变形预测
受内部结构与外部多种因素的综合影响,滑坡变形在时间尺度上具有趋势性、周期性、脉动性与随机性等4个变化特征[10]。在长时间的非线性演化过程中表现为较明显的混沌状态[11]。因此,对滑坡时间序列进行混沌分析挖掘出隐含于序列中的特性,再建立预测模型,成为研究滑坡变形的常用方法。
2.1小波变换原理
小波变换具有多分辨率分析的特点,具备随频率变化而改变“时间-频率”窗口大小的能力,在时频分析、信噪分离等工程技术领域有广泛应用。其变换过程是通过平移和缩放运算对信号进行多尺度细化,对信号的低频、高频部分使用不同的频率分辨率与时间分辨率进行处理,最终达到高频部分时间细分、低频部分频率细分的目的,从而可以精确反映信号的任意细节[6]。
利用小波变换进行数据分析时,首先要选择小波函数和确定小波分解层数。几种常见的小波函数有Haar小波、morlet小波、db系列小波和maar小波等。而对于小波分解层数的选择没有成熟的理论依据。在进行较多层数的小波分解时,虽然高低频信号的稳定性及平滑性较好,但在分解过程中受到计算误差及信息流失的影响变大,最终造成预测精度的降低。设基函数满足容许条件[12]:

(3)
定义
(4)
式中: a为尺度因子; b为平移因子; φ(a, b)(t)是由小波母函数φ(w)生成的依赖于参数(a,b)的连续小波, 则小波变换为
Wf(a,b)=∫f·φ(a,b)(t)dt,
(5)
进而得出小波变换的反变换,即采用Wf(a,b)重构f(t):
(6)
2.2滑坡分解及预测实验流程
本文采用mallat方法对滑坡原始序列进行分解与重构,其中对不同分量组合的各个分量使用RBF神经网络预测模型进行预测。本文对滑坡序列的分解与预测模型的流程如图1所示。

图1 模型预测流程图Fig.1 Flow chart of model prediction
首先, 采用mallat方法对滑坡原始序列进行分解与重构。 对于滑坡序列{x(t), t=1, 2, …, n},mallat方法的每一层分解得到一个低频分量c和高频分量d, 其往后的每层分解是对前一层分解得到的低频分量进行再分解的过程, 因此进行n层分解后得到一个低频分量cn与n个高频分量d1, d2, …, dn。
其次,在完成小波分解后,本文对各层分解结果采用3种不同的分量组合方案建立预测模型:
① 低频-全部高频分量组合预测,即对小波分解得到的低频分量与全部的高频分量,分别建立RBF神经网络预测模型进行预测,最后叠加各分量预测值即为预测结果;
② 低频-部分高频分量组合预测,即对低频分量与部分高频分量建立RBF神经网络预测模型;
③ 低频分量预测,即忽略全部的高频分量,仅对低频分量建立RBF神经网络预测模型。
2.3精度评定
为综合评定模型预测的精度,本文采用均方根误差(MSE)与平均绝对值误差(MAE)来评价滑坡变形预测的效果:
① 均方根误差(MSE)
(7)
② 平均绝对误差(MAE)
(8)

3算例分析
以丹巴滑坡变形序列[13]为实验数据,按照本文前述的方案对其进行分析。该滑坡区属于青藏高原东缘的大渡河高山峡谷区,区内山峦起伏,地形陡峻,海拔介于1 887~2 110 m,地表变形较为明显。本文选取第6号监测点的监测数据(2005-01-31—2005-04-16)进行分析,观测数据共76期,如图2所示。
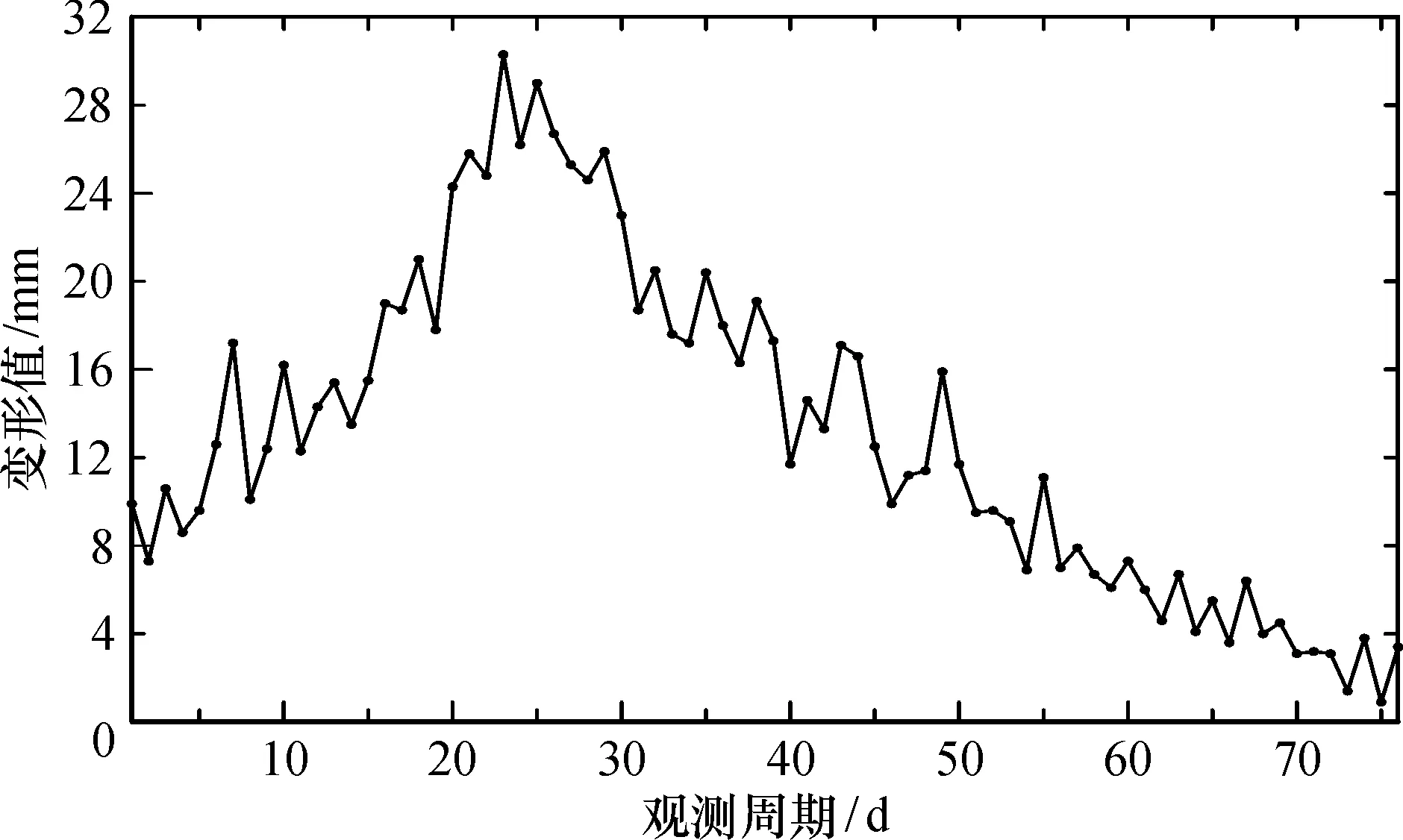
图2 监测点滑坡位移变形序列Fig.2 Deformation sequence of landslide displacement
可见,滑坡变形较为剧烈,非线性、非平稳性与随机性较为突出,变形的幅度比较大,变形由上升趋势变为下降趋势,形成一个较为尖锐的凸峰,变形最大值与最小值之间相差29.4 mm,具有一定的代表性。显然,如果利用传统的预测方法很难真实反映滑坡的变形趋势。根据经验,小波分解一般选择3层分解,则分解结果如图3所示。
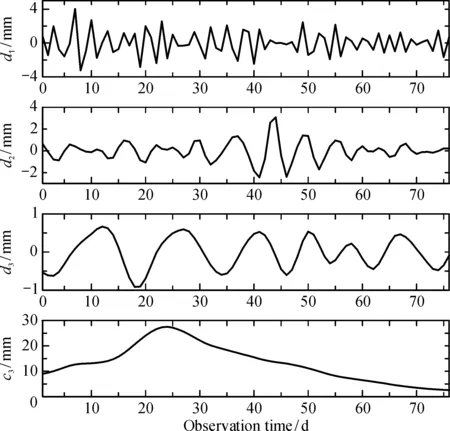
图3 滑坡时间序列的3层小波分解结果Fig.3 Wavelet decomposition results of landslide time series
小波分解将滑坡序列分解为趋势项与干扰项,c3变化较为平稳,有利于模型的建立和预测;高频分量d1、d2以及d3的频率逐级递减,较原始序列其非平稳特性已得到有效降低,但仍存在较强的随机性和噪声干扰项,不利于提高预测精度。
为研究小波分解层数、 分量组合形式以及不同的预测步长对滑坡预测精度的影响, 按照前文所述的3种分量组合方案进行RBF神经网络模型预测。在所有实验中, 选择各分解分量的50个数据作为RBF模型的学习样本, 对应于变形数据的后10个数据作为预测检验样本; 预测步长表示超前预测的天数; 小波分解的层数分别为1~5层, 小波分解的层数愈多, 其低频-高频分量组合的形式愈多。上述3种分量组合方案的预测精度见表1、 表2。
通过对上述实验结果进行比较可知:
(1)增加小波分解层数,有利于预测精度的提高。从表1、2、3得知,预测步长相同的情况下,预测精度最高的均进行了4或5层分解,1~3层分解对应的预测精度相对较低。而且进行4层或5层分解再建模预测的效果相差不大。这说明适当地提高分解层数,可以提高变形序列中趋势项和干扰项的分离程度,有利于减小干扰因素引起的不利影响,提高预测精度。

表1 滑坡变形预测的MSE与MAE指标(步长:1~5)Table 1 MSE and MAE index of landslide deformation prediction(predictive step from 1 to 5)

表2 滑坡变形预测的MSE与MAE指标(步长:6~10)Table 2 MSE and MAE index of landslide deformation prediction(predictive step from 6 to 10)
在表1、表2中,加黑部分表示在对应的预测步长与分解层数下最优分量组合的预测精度。为了便于分析,表3则统计了各预测步长与小波分解层数条件下,预测精度最优的分量组合,其中加黑部分表示在相同预测步长条件下,不同分解层数的全部组合中取得最高预测精度的最优分量组合。图4为4层分解时c4d4d3分量组合预测步长与预测精度的关系,两者存在反比关系。

表3 滑坡变形预测最优分量组合Table 3 Optimal components combination of landslide deformation prediction

图4 c4d4d3组合预测步长与预测精度的关系Fig.4 Relationship between predietion aceuracy and predictive steps in c4d4d3
(2)增大预测步长不利于提高预测精度。从表1、2以及图4中不难看出,随着预测步长的增加,预测误差也出现不同程度的增大,且预测误差增加的幅度变大。当进行1~5步预测时,进行4层分解并采用c4d4d3分量组合时可以得到最优的预测精度。进行6步或以上的预测时,进行5层分解并采用c5d5分量组合可得到最优预测精度。
(3)合理选择分量组合可以提高预测精度。表1、2详细列举了不同分量组合的预测精度,显然不同的分量组合其预测结果是不相同的。对于3、4、5层分解,预测时若忽略d1与d2高频分量,采用低频-部分高频分量组合则可以使预测精度得到显著提高;而进行n层小波分解后(本文n≥3),忽略全部的高频分量而仅采用低频分量cn进行预测并不能得到最优的预测效果。另外, 对于4、 5层分解, 忽略了d1与d2高频分量的各种低频-部分高频分量组合的效果相当, 如5层分解中预测步长为1时, c5d5d4d3、 c5d5d4、 c5d5的预测结果分别为1.576、 1.599与1.600。以上分析表明, 在d1、 d2高频分量中随机信息和干扰项较多, 不宜用于变形预测; 而当高频分量(如d5、 d4)中的干扰项引起的预测误差可以忽略不计时, 剔除高频分量会导致预测精度降低。
综合来看, 适当增加小波分解层数, 减小预测步长, 采用低频-部分高频分量组合(不包含d1、 d2高频分量)进行滑坡变形预测能有效提高预测精度。 上述实验中的预测步长为1~5时, 采用4层分解的效果最好, 其最优组合为c4d4d3分量组合(见表3中加黑部分); 对于6步及以上步长的预测, 进行小波5层分解最好, 其对应的最优分量组合为c5d5。
4结论
利用滑坡变形序列对本文模型进行了验证,从小波分解层数、分量组合以及预测步长三方面对实验结果进行了分析。基于本文的实验,进行4或5层分解采用低频-部分高频分量组合进行预测可以达到较优的精度。这一结论对滑坡变形预测具有参考意义,而在其他的变形预测应用中,为了取得最优的预测效果,确切的分解层数与分量组合可以先通过实验进行确定。
参考文献:
[1]曹洋兵,晏鄂川,谢良甫.考虑环境变量作用的滑坡变形动态灰色-进化神经网络预测研究[J].岩土力学,2012,33(3):848-852.
[2]徐峰,汪洋,杜娟,等. 基于时间序列分析的滑坡位移预测模型研究[J]. 岩石力学与工程学报,2011,30(4):746-751.
[3]吴益平,滕伟福,李亚伟. 灰色-神经网络模型在滑坡变形预测中的应用[J]. 岩石力学与工程学报,2007,26(3):632-636.
[4]陆付民,王尚庆,李劲,等. 顾及地下水位因子的卡尔曼滤波模型在滑坡变形预测中的应用[J]. 武汉大学学报:信息科学版,2010,35(10):1184-1187.
[5]林大超,安凤平,郭章林,等. 滑坡位移的多模态支持向量机模型预测[J]. 岩土力学,2011,32(S1):451-458.
[6]王新洲, 范千,许承权,等. 基于小波变换和支持向量机的大坝变形预测[J]. 武汉大学学报:信息科学版,2008,33(5):469-471.
[7]梁月吉,任超,刘立龙,等.基于EMD和GA-BP神经网络的大坝变形预测[J].桂林理工大学学报,2015,35(1):111-116.
[8]李潇,徐进军. 基于小波分析与 LSSVM 的滑坡变形预测[J].大地测量与地球动力学,2009,29(4):127-130.
[9]吕金虎,陆君安,陈士华.混沌时间序列分析及应用[M].武汉:武汉大学出版社,2002:57-80.
[10]姚林林,殷坤龙,陈丽霞,等. 基于影响因子分析的滑坡位移预测模型研究[J]. 安全与环境工程,2006,13(1):19-22.
[11]秦四清,张倬元.滑坡灾害可预报时间尺度问题探讨[J].中国地质灾害与防治学报,1994,5(1):17-22.
[12]张德峰.MATLAB 小波分析[M].北京: 机械工业出版社,2011.
[13]梁莉.基于相空间重构理论的滑坡预测研究[D]. 成都:成都理工大学, 2008:34-35.
文章编号:1674-9057(2016)02-0304-06
doi:10.3969/j.issn.1674-9057.2016.02.018
收稿日期:2015-05-22
基金项目:国家自然科学基金项目(41461089);广西空间信息与测绘重点实验室项目(13-051-14-09;13-051-14-15)
作者简介:卢献健(1982—),男,硕士,讲师,研究方向: GPS应用及变形数据处理,2008056@glut.edu.cn。
通讯作者:晏红波,博士研究生,56403075@qq.com。
中图分类号:P258
文献标志码:A
Analysis of wavelet decomposition and wavelet component combination for landslide prediction
LU Xian-jian,YAN Hong-bo,LIANG Yue-ji
(a.College of Geomatics and Geoinformation; b.Guangxi Key Laboratory of Spatial Information and Geomatics, Guilin University of Technology, Guilin 541004,China)
Abstract:Based on the characteristics of non-stationary, non-linear and stochastic landslide deformation changes, a combination method of wavelet decomposition and RBF neural network is proposed for the landslide prediction. Based on experiments of wavelet decomposition and prediction of the combination of different low frequency and high frequency components,the effect of different wavelet decomposition levels,the component combination and predictive steps is analyzed.The experimental results show that only the appropriate decomposition level, proper component of combination and predictive step are selected, can we obtain optimal prediction. Also, the correctness of the method in the paper is verified. All these studies and results provide reference for the predication of landslide.
Key words:landslide prediction;wavelet decomposition;wavelet component combination;RBF neural network
引文格式:卢献健,晏红波,梁月吉.小波分解层数及分量组合对滑坡预测的影响[J].桂林理工大学学报,2016,36(2):304-309.
