关于两类拉伸杆的斜截面应力分布的探究

王金城，王柳菁

（大连理工大学运载工程与力学学部，辽宁大连 116024）

关于两类拉伸杆的斜截面应力分布的探究

王金城，王柳菁

（大连理工大学运载工程与力学学部，辽宁大连 116024）

在大多数工程实践中，细长杆件都是忽略自重的，但是某些特殊情况下，杆件的自重是不可忽略的，其自重给杆内应力带来的影响直接关乎该杆件的强度校核。为了使工程中杆件的设计与应用更加安全可靠，本论文研究了拉伸杆件的在考虑自重和不考虑自重两类情况下的杆内各点应力的分布情况，运用局部化思想解决杆件截面受力不均匀的难题，并得出两类杆的各点应力准确计算公式。

局部化思想；应力分布；应力不均

1 问题描述

以下两种情况下：（1）忽略杆件自重并将与自重等大的轴力施加于杆件末端（2）考虑杆件自重。如何确定同一杆件同一斜截面上同一点的应力。

2 问题分析

2.1 受轴向集中载荷无自重杆

针对第一种情况，由于Fp是施加在杆件轴线上的，结合材料力学的均匀、连续、各向同性的基本假设，可知杆内的内力是均匀分布的，且斜截面上应力是处处相等的。

假设斜截面与杆件横向成α角度，则截开后的面上轴向方向的内力是相同的，将这些内力都向轴线简化，可α得到总的轴力也为Fp。现以平行于斜截面方向为x轴，垂直于斜截面为y轴建立直角坐标系，将力Fp分别投影到两坐标轴上，分别记为FN和FQ。

其中

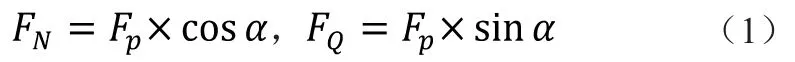
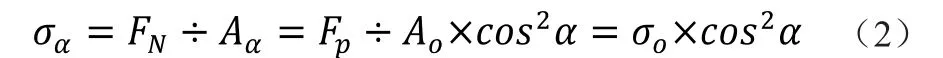
切应力为

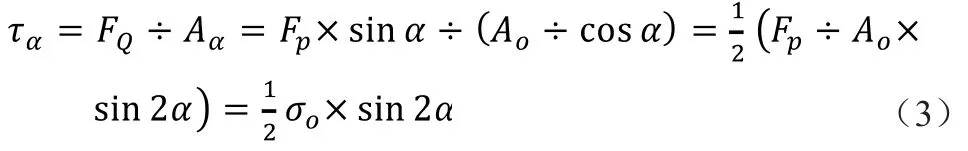
故分析公式可知任意斜截面上的任意点的应力只与斜截面和杆件横向方向之间的夹角a有关，而与斜截面的位置、点在斜截面上的位置无关。

当α=0°时，正应力σα最大，最大值为

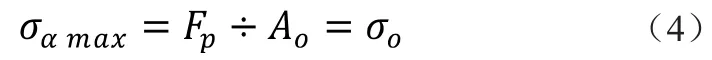
当α=45°时，切应力最大，最大值为

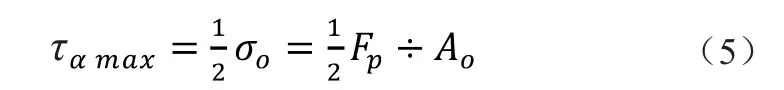
2.2 自重不可忽略杆

针对第二种情况，已知均布载荷为p kN/m3，故斜截面上轴线方向上的应力不是均匀分布的，故对斜截面上应力计算带来了不便。换个思路，我们可以运用局部化分析思想来解决这个问题。

在斜截面处沿横截面方向、纵截面方向切出一个小立方体微元，沿长度方向的长度为δx，设立方体微元上表面A的横坐标为xo，下表面B的横坐标为xo+δx。由于A、B面都是沿横截面切下的，故面内只有正应力，下面对A、B面正应力进行计算。设杆件长为L，横截面长为a，宽为b。现对A面进行受力分析，设A面所在横截面受力为Fxo，方向为正方向，则A’面所在横截面受力Fx′o与Fxo互为相反力，求出Fx′o相当于求出Fxo。则首先对整根杆做受力分析得杆的最上端受力

方向为x轴负方向。对A’面列平衡方程

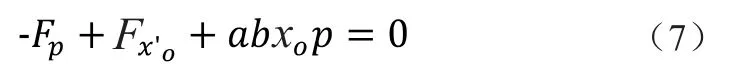
解得

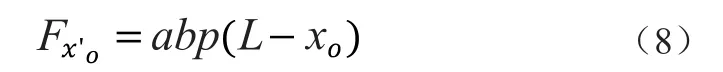
则

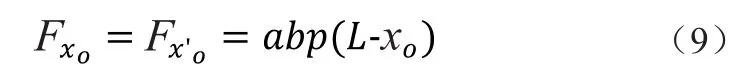
同理，对B面列平衡方程

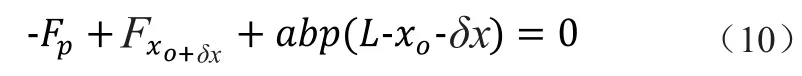
解得

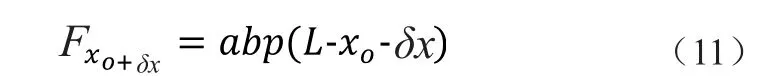
由于δx足够小，故

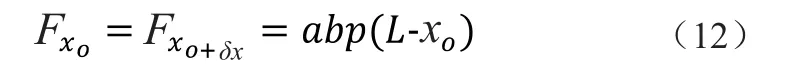
故微元的上下表面所受力大小可近似看做相等，那么微元体内内力可看做均匀分布。此时，可在微元体内任意用假想平面切分，进而研究截面内的应力分布。下面采用和第一种情况相类似的斜面切割法，用与横截面成α角斜截面将微元体切分为两半，任取一半进行分析。方法与第一种情况完全类似，唯一区别为将第一种情况里的Fp替换为Fxo。则由式（2）得斜截面正应力

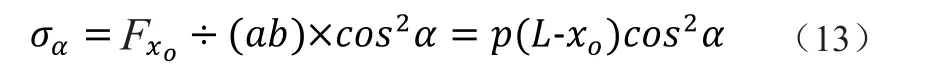
由式（3）得斜截面切应力

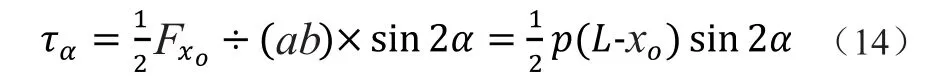
由公式（13）可知，在考虑自重的情况下斜截面上一点的正应力和切应力的大小不仅与斜截面和杆件横向方向的夹角α有关，还与点所在位置的横坐标xo有关，当α大小确定时，xo越大应力越小；xo越小，即越接近杆的根部，应力越大。

当xo=0，α=45°时，截面内正应力最大，最大值为

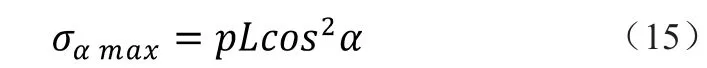
当xo=0，α=45°时，该点处的切应力最大，最大值为

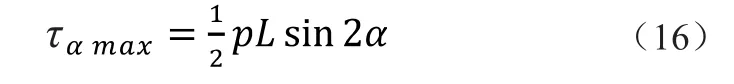
3 结论

对比两种情况最终的应力公式（2）（3）（13）（14）发现，同一斜截面上的各点的应力分布是不同的，不考虑自重情况下，同一斜截面上的点的应力分布相同，即在其他条件不变的情况下，应力大小只与斜截面角度α有关。也就是说杆件任意与轴线成确定角度的斜截面上的点的应力是相等的，且将斜截面沿轴线平移到任何位置，应力大小都不变化，因此由公式（5）可计算最大切应力。

杆件自身重力不可忽略时，同一斜截面上的点的应力分布是不均匀的，即杆件内一点处的应力大小不仅与斜截面角度α有关，还与点所在位置的沿杆长度方向的坐标x有关。

通过以上分析，可以清楚地认识到考虑自重与忽略自重两种情况下，斜截面应力分布的计算方法的异同，该结论可以应用到工程实际中。

[1]季顺迎.材料力学[M].北京：科学出版社，2013.

Explore the Oblique Section on Types of Ttress Distribution in the Stretch Rod

Wang Jin-cheng，Wang Liu-qing

In most cases，people are learning and research are ignored rod weight，but in some special cases，the weight of the rod is not negligible，its weight to the impact of stress caused by the inner rod may be directly related to the strength check rods，in order to make the design and application engineering rod is more secure and reliable，this thesis studied a stretch considering the weight of the rod and does not consider the weight of the various types of stress at the inner rod in case of distribution，as long as the use of a localized thinking to solve a cross-section rods discontinuity problem，the conclusion that the two types of stem stress points to accurately calculate the formula.

localized thinking；Uneven stress；Stress distribution

U448.213

A

1003–6490（2016）04–0246–02

2016–04–08

王金城（1994—），男，四川江油人，本科在读生，主要从事工程力学学习与研究工作。