利用引力梯度数据计算径向梯度的优化方法

孟祥超，万晓云，于锦海，朱永超, 冯　炜

1. 中国科学院计算地球动力学重点实验室，北京 100049; 2. 钱学森空间技术实验室，北京100094; 3. 中国科学院测量与地球物理研究所，湖北 武汉 430077; 4. 北京卫星导航中心，北京 100049



利用引力梯度数据计算径向梯度的优化方法

孟祥超1，万晓云2，于锦海1，朱永超1, 冯炜3,4

1. 中国科学院计算地球动力学重点实验室，北京 100049; 2. 钱学森空间技术实验室，北京100094; 3. 中国科学院测量与地球物理研究所，湖北 武汉 430077; 4. 北京卫星导航中心，北京 100049

Foundation support： The National Natural Science Foundation of China (Nos. 41404019; 41274034)；The National High-tech Research and Development Program of China (863 Program) (No.2013AA122502-2)；The Open Fund of State Key Laboratory of Geodesy and Earth’s Dynamics (No.SKLGED2014-3-5-E)

摘要：根据重力梯度观测各分量的方差及协方差信息，提出了利用GOCE梯度数据计算径向重力梯度的优化方法。首先给出了径向重力梯度的计算方法，并深入分析了误差传播规律，通过建立相应的条件极值问题，给出了计算径向重力梯度最优组合因子的方法；通过模拟数据验证了本文所提出的优化因子的优越性。实际数据计算表明：相对于传统方法，采用优化组合因子可使反演所得引力位模型的累积大地水准面精度在250阶时提高约2 cm。由于径向重力梯度不仅可以用于地球引力场模型的求解，也可直接应用于地球物理问题的讨论，因此本文所提出的优化方法也可对部分地球动力学问题的讨论提供方便。

关键词：GOCE; 径向重力梯度; 优化方法；精度

GOCE卫星[1]于2009年3月17日发射升空，2013年11月11日降落，提供的梯度数据观测点数超过1亿。围绕如何利用该颗卫星的数据进行引力场反演，受到了学者们的广泛关注[2-6]，官方也陆续发布了10多个GOCE引力场模型，所采用的方法主要包括直接法、时域法和空域法[4,7]。

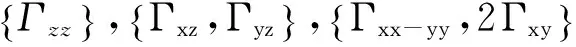
对于GOCE观测数据而言，径向梯度并不是直接的观测量，而接近径向的分量Vzz的精度低于Vxx和Vyy[16]，这就为构建关于径向梯度的边界条件时如何保证其精度提出了挑战。如何在某种最优的条件下给出径向梯度的计算方法对处理GOCE实际数据是至关重要的。

文献[16]对GOCE的引力梯度观测值采用新的组合方法，有效提高了Vzz方向分量的精度，并据此对东京地震所引起的重力变化进行了讨论；文献[17]采用同样的组合[16]对南极冰川的质量变化进行了讨论。由此自然产生了这样的问题：能否得到径向梯度Vrr的最优组合？此外上述文献优化组合的前提是假设Vxx、Vyy和Vzz相互独立，但没有给出为何能作此假设。即便如此，上述文献所使用的组合方法也并不是最优的方法。

本文的目的是研究如何从GOCE梯度数据来最优地组合出径向梯度分量Vrr。第1部分是对径向梯度的计算方法进行介绍，并深入分析其误差传播规律。第2部分是对如何构建优化组合因子进行阐述，并计算得到有关因子。第3部分通过模拟数据验证上述组合因子的优越性，然后通过实际数据计算验证本文算法；最终对本文所采用的方法及其在GOCE数据处理中需要注意的问题进行了总结。

1径向扰动梯度的构建

1.1径向梯度的计算及其误差传播

GOCE观测的梯度分量在梯度仪观测坐标系下给出，用Vij(ij=xx，yy，zz，xy，xz，yz)表示。为了得到地固坐标系下的值，可按下式进行坐标转换

(1)

式中，R为梯度仪坐标系和地固坐标系之间的转换矩阵。由于低频误差的存在，且V12、V23精度太差无法使用，上述的坐标变换一般基于扰动分量来进行，即首先计算出梯度观测值相对参考值的差异并作低频滤波处理，然后再进行坐标变换，其中V12和V23的观测值由参考引力位计算值代替。若只考虑径向扰动梯度，现利用各坐标轴与地球径向的夹角，在非全张量观测的情况下可得到式(2)[15]

Trr=T33cos2α3+T22cos2α2+T11cos2α1+

2T13cosα1cosα3

(2)

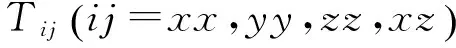
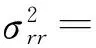
(3)

式中

根据文献[15]，可知z方向和地球径向十分接近，夹角最大值小于1.5°。利用2010年1月1日—2010年3月1日的姿态观测数据，可得表1。

表1　径向梯度误差传播系数统计

δ33=δ13=2δ22=2δ11=2δ0

(4)

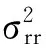
第1步，利用FIR向前向后带通滤波器对原始GOCE梯度数据(EGG_NOM2)相对于EIGEN5C前300阶次计算值的差值进行带通滤波处理，滤波通带为0.005～0.1Hz，原始数据的时间段为2010年1月1日—2010年3月1日，最终得到测量通带内的观测值。采用带通滤波器的目的是消除低频误差的影响；采用参考引力位的目的是消除趋势项信息[18]。

第2步，利用滤波后的残差值计算出各量之间的相关系数，统计结果见表2。

表2各分量测量带宽内信号相关系数统计

Tab.2Correlation between different components of gravity gradient residuals in MBW

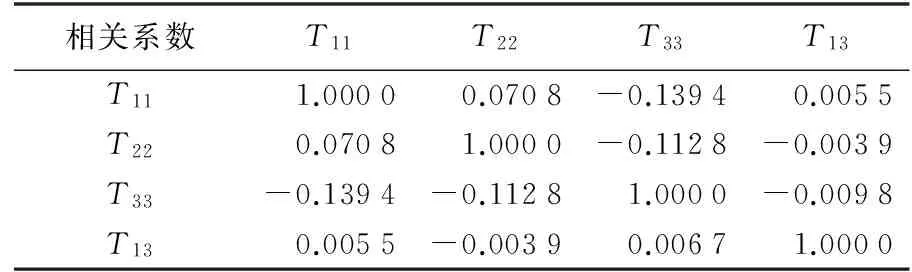
相关系数T11T22T33T13T11 1.0000 0.0708-0.1394 0.0055T220.07081.0000-0.1128-0.0039T33-0.1394-0.11281.0000-0.0098T130.0055-0.00390.00671.0000

1.2最优组合因子的选取

由以上分析可知，T33的精度直接影响着Trr的计算精度。在独立分布的前提下，文献[16]采用下式来重新计算得到T33

(5)

这使得T33,c的精度相比于T33提高了1.64倍，误差降低了40%[17]。这也将导致Trr精度的提升。事实上，该种组合并不是最优的组合。本文通过建立如下的极值问题来找出最优的比例因子

(6)

其解为

(7)

(8)

T11cos2α1+2T13cosα1cosα3

(9)

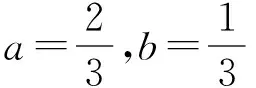
2算例

为了验证上节结论，现通过建立如下的边值问题来进行讨论

(10)

式中，f由式(9)计算得到。该边值问题的求解可参见文献[15]

(11)

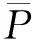
2.1模拟数据分析

首先利用EGM08模型[22]前250阶完整阶次在GOCE卫星的平均轨道高度上按经纬度25′×25′等间隔模拟出梯度张量六分量，坐标系选为地方指北坐标系，将上述模拟值作为观测值；然后按正态分布模拟随机噪声，各分量噪声均值为0，方差相对比例同式(4)，其中δ0为1mE。最后构建如式(10)所示的边值问题进行引力场恢复，参考引力位为EIGEN5C。图1给出了最终结果同引力位EGM08模型的阶方差，可视为真误差。

图1中所有结果是直接计算得到的结果而未作迭代计算，Variance_noerror表示不添加误差利用Tzz恢复得到的引力位模型的误差阶方差；Variance_adderror表示添加误差后直接利用Tzz恢复得到的引力位模型的误差阶方差；Variance_com表示添加误差后利用本文所提出的组合因子重新计算Tzz，然后利用新的Tzz恢复得到的引力位模型的误差阶方差。由该图可知，由于观测误差的存在，引力位模型恢复的精度下降明显；采用组合算法的结果相对于不采用组合算法，精度有明显提升。

2.2实际数据计算结果分析

本节主要采用实际的GOCE引力梯度数据来验证本文所述方法的优越性。如前所述，原始的梯度数据含有大量级的低频误差，必须首先对其进行处理。本文采用FIR带通滤波器进行零相位滤波[23]来处理低频噪声，参考引力位为EIGEN5C前300阶；接着采用本文所述的优化方法来重新计算梯度坐标系下的Tzz，并进一步得到Trr；然后对其数据进行格网化，方法采用反距离加权算法[24-25]；最终通过解算如式(10)所述的边值问题计算得到引力位模型。该计算所采用的梯度数据为GOCE卫星Level 2所提供的EGG_NOM2，轨道数据由SST_PSO_2提供，时间段为2009年11月1日—2012年8月1日。

论文采用两种方法来恢复得到引力位，第1种是对滤波后的扰动梯度数据直接进行坐标变换，得到地方指北坐标系下的径向引力梯度数据，然后通过求解边值问题得到引力位模型，结果令为EGMQLSTTrr，可视为传统方法；第2种方法是通过论文提出的优化组合因子得到Tzz,并进一步地得到Trr，然后通过求解边值问题得到引力位模型，结果令为EGMQLSTTrrCom。为了对模型的精度进行评估，现选用两个引力位模型进行对比分析：一是EGM08模型，该模型的研制采用了多种类型的观测数据，是当前精度最高的引力位模型之一；另外一个模型是EGMD4，该模型是官方利用直接法恢复得到的第4组GOCE引力场模型，所采用数据的时段为2009年11月1日—2012年8月1日，与本文所采用数据的时间段相同。图2、图3分别给出了引力位模型EGMQLSTTrr、EGMQLSTTrrCom相对于EGM08模型的阶方差和大地水准面累积差异信息；图4、图5则分别给出了引力位模型EGMQLSTTrr、EGMQLSTTrrCom相对于EGMD4模型的阶方差和大地水准面累积差异信息。

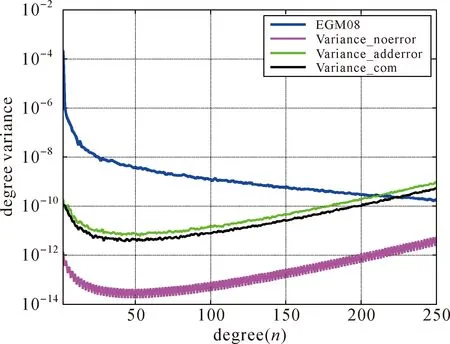
图1　误差阶方差Fig.1　Degree variations to EGM08

若将EGM08模型看作真值，由图2(a)可知，EGMQLSTTrrCOM的有效阶数超过250阶，优于EGMQLSTTrr；由图2(b)可知，相对于参考引力位模型EIGEN5C，EGMQLSTTrr在100～210阶精度有明显改进，EGMQLSTTrrCom则在100～220阶有明显改进，而在190～260之间的阶数，EGMQLSTTrrCom精度明显高于EGMQLSTTrr。由图3可知，在200阶时，EGMQLSTTrr、EGMQLSTTrrCom大地水准面的精度优于EIGEN5C大约4cm，而在200阶以后，EGMQLSTTrrCom精度明显优于EGMQLSTTrr，在250阶时，前者优于后者2cm，在260阶时大约优于3.5cm。由于采用了相同的观测数据，因此上述结果表明采用本文所提出的优化因子能够提高GOCE数据处理的精度，特别是对于引力场模型高阶项恢复的精度。

图2　与EGM08的差异阶方差Fig.2　Degree variance differences between EIGEN5C, EGMQLSTTrr, EGMQLSTTrrCom and EGM08

若将官方所发布的模型EGMD4看作真值，由图4可知,EGMQLSTTrr、EGMQLSTTrrCom在阶数80～230明显优于参考引力位模型EIGEN5C。若按大地水准面的精度，根据图5可知，在200阶时EGMQLSTTrr、EGMQLSTTrrCom精度相当，优于EIGEN5C大约7cm；从180阶开始，EGMQLSTTrrCom逐渐优于EGMQLSTTrr，在250阶时精度可高约2cm，而在260阶时，精度可高约近4cm。上述结果与图2、图3的结果一致，均显示了采用优化因子计算径向梯度的优越性。

图3　与EGM08大地水准面累积差异Fig.3　Cumulative geoid differences between EIGEN5C, EGMQLSTTrr, EGMQLSTTrrCom and EGM08

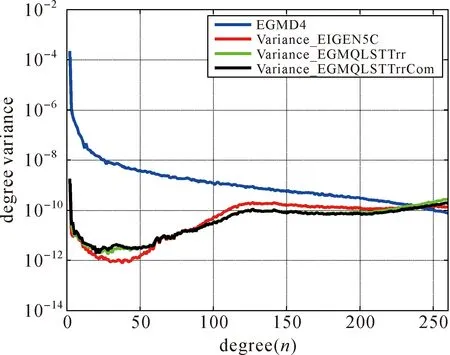
图4　与EGMD4的差异阶方差Fig.4　Degree variance differences between EIGEN5C, EGMQLSTTrr, EGMQLSTTrrCom and EGMD4

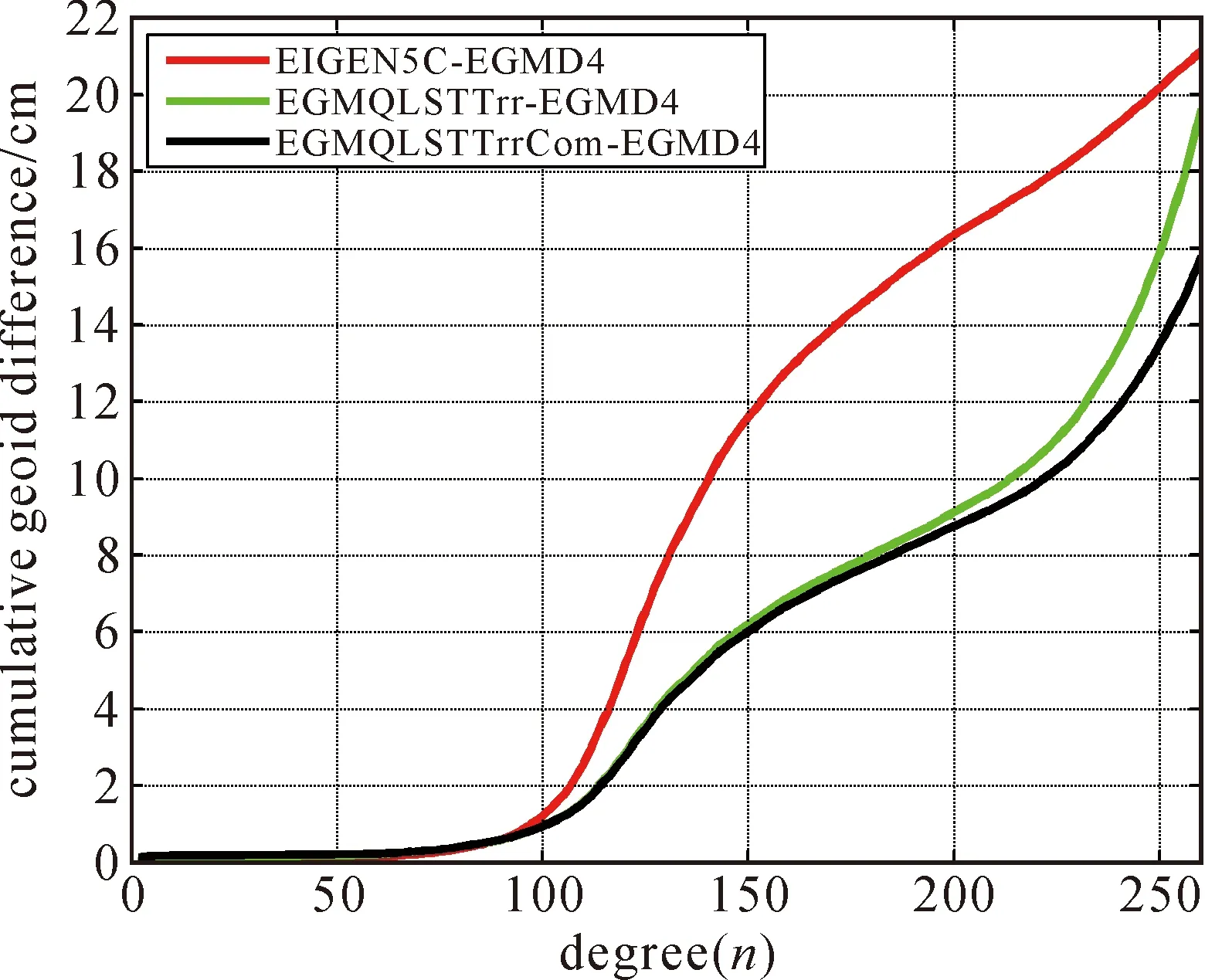
图5　与EGMD4的累积大地水准面差异Fig.5　Cumulative geoid differences between EIGEN5C, EGMQLSTTrr, EGMQLSTTrrCom and EGMD4

3结论

本文从引力梯度张量观测误差及协方差统计特性出发，建立了计算径向梯度的优化方法。通过模拟数据，验证了该算法能明显地改善径向梯度相应的边界条件。

采用本文所给出的优化方法处理GOCE实际数据，得到了相应的重力场模型。与不采用优化方法所得的模型相比，优化处理后的模型在计算大地水准面时(至250阶)精度可提高约2cm。

本文方法的前提是已知各分量的方差信息和协方差信息，而这往往是比较困难的。事实上，本文所需要知道的并不是各分量方差和协方差分量的绝对量值，而是各量的相对比例。本文采用的是文献[16]所给出的方差相对比例值(用式(4)表示)，实际上也可通过迭代计算[26]，利用验后方差分量估计来得到各分量的方差和协方差信息。

最后关于GOCE引力梯度观测数据进行一些说明。由于引力梯度数据在低频部分是不准确的，因此如何处理引力梯度数据的低频部分是很重要的课题，多篇文献对此进行了讨论与研究[23, 27]。若能够有效结合GOCE低频误差的处理方法和本文所述的优化方法，则可更好地提高GOCE梯度数据处理的精度。总之，由于径向梯度具有丰富的地球物理意义，因此本文的工作不仅能有助于提高GOCE重力场模型的恢复精度，而且对许多地球物理问题的研究也会有一定的帮助。

致谢：感谢欧空局提供GOCE梯度数据。

参考文献：

[1]BALMINO G, RUMMEL R, VISSER P, et al. Gravity Field and Steady-State Ocean Circulation Mission[R]. The Four Candidate Earth Explorer Core Missions. Noordwijk: ESA Publications Division, 1999.

[2]REGUZZONI M, TSELFES N. Optimal Multi-step Collocation: Application to the Space-Wise Approach for GOCE Data Analysis[J]. Journal of Geodesy, 2009, 83(1): 13-29.

[3]PAIL R, BRUINSMA S, MIGLIACCIO F, et al. First GOCE Gravity Field Models Derived by Three Different Approaches[J]. Journal of Geodesy, 2011, 85(11): 819-843.

[4]PAIL R, GOIGINGER H, SCHUH W D, et al. Combined Satellite Gravity Field Model GOCO01S Derived from GOCE and GRACE[J]. Geophysical Research Letters, 2010, 37(20): L20314.

[5]YI Weiyong. An Alternative Computation of A Gravity Field Model from GOCE[J]. Advances in Space Research, 2012, 50(3): 371-384.

[6]YU Jinhai, WAN Xiaoyun. Recovery of the Gravity Field from GOCE Data by Using the Invariants of Gradient Tensor[J]. Science China Earth Sciences, 2013, 56(7): 1193-1199.

[7]RUMMEL R, GRUBER T. Product Acceptance Review (PAR)-Level 2 Product Report[R]. Noordwijk: ESA, 2012.

[8]RUMMEL R, VAN GELDEREN M. Spectral Analysis of the Full Gravity Tensor[J]. Geophysical Journal International, 1992, 111(1): 159-169.

[9]朱灼文, 于锦海. 超定大地边值问题的准解[J]. 中国科学(B辑), 1992(1): 103-112.

ZHU Zhuowen, YU Jinhai. Pseudo-Solution on Geodetic Overdetermined Boundary Value Problems[J]. Science in China (Series B), 1992, 35(6): 697-708.

[10]罗志才. 利用卫星重力梯度数据确定地球重力场的理论和方法[D]. 武汉: 武汉测绘科技大学, 1996. LUO Zhicai. The Theory and Methodology for Determining the Earth’s Gravity Field Using Satellite Gravity Gradiometry Data[D]. Wuhan: Wuhan Technical University of Surveying and Mapping, 1996.

[11]VAN GELDEREN M, RUMMEL R. The Solution of the General Geodetic Boundary Value Problem by Least Squares[J]. Journal of Geodesy, 2001, 75(1): 1-11.

[12]吴星. 卫星重力梯度数据处理理论与方法[D]. 郑州: 信息工程大学, 2009.

WU Xing. Theory and Methods of Satellite Gradiometry Data Processing[D]. Zhengzhou: Information Engineering University, 2009.

[13]于锦海, 赵东明. 引力梯度不变量与相关边界条件[J]. 中国科学 D辑: 地球科学, 2010, 40(2): 178-187.

YU Jinhai, ZHAO Dongming. The Gravitational Gradient Tensor’s Invariants and the Related Boundary Conditions[J]. Science China Earth Sciences, 2010, 53(5): 781-790.

[14]刘晓刚. GOCE卫星测量恢复地球重力场模型的理论与方法[D]. 郑州: 信息工程大学, 2011. LIU Xiaogang. Theory and Methods of the Earth’s Gravity Field Model Recovery from GOCE Data[D]. Zhengzhou: Information Engineering University, 2011.

[15]WAN Xiaoyun, YU Jinhai. Derivation of the Radial Gradient of the Gravity Based on Non-full Tensor Satellite Gravity Gradients[J]. Journal of Geodynamics, 2013, 66(2): 59-64.

[16]FUCHS M, BOUMAN J, BROERSE T, et al. Observing Coseismic Gravity Change from the Japan Tohoku-Oki 2011 Earthquake with GOCE Gravity Gradiometry[J]. Journal of Geophysical Research, 2013, 118(10): 5712-5721.

[17]BOUMAN J, FUCHS M, IVINS E, et al. Antarctic Outlet Glacier Mass Change Resolved at Basin Scale from Satellite Gravity Gradiometry[J]. Geophysical Research Letters, 2014, 41(16): 5919-5926.

[18]赫尔默特·莫里兹. 高等物理大地测量学[M]. 宁津生, 管泽霖, 译. 北京: 测绘出版社, 1984: 194-198. MORITZ H. Advanced Physical Geodesy[M]. NING Jinsheng, GUAN Zelin, Trans. Beijing: Surveying and Mapping Press, 1984: 194-198.

[19]ESA. GOCE Level 1b Products User Handbook[R]. GOCE-GSEG-EOPG-TN-06-0137. Noordwijk: ESA, 2008.

[20]RUMMEL R, YI Weiyong, STUMMER C. GOCE Gravitational Gradiometry[J]. Journal of Geodesy, 2011, 85(11): 777-790.

[21]YI Weiyong, RUMMEL R, GRUBER T. Gravity Field Contribution Analysis of GOCE Gravitational Gradient Components[J]. Studia Geophysica et Geodaetica, 2013, 57(2): 174-202.

[22]PAVLIS N K, HOLMES S A, KENYON S C, et al. An Earth Gravitational Model to Degree 2160: EGM2008[C]∥Presented at the 2008 General Assembly of the European Geosciences Union. Vienna: [s.n.], 2008.

[23]万晓云, 于锦海, 曾艳艳. GOCE引力梯度的频谱分析及滤波[J]. 地球物理学报, 2012, 55(9): 2909-2916. WAN Xiaoyun, YU Jinhai, ZENG Yanyan. Frequency Analysis and Filtering Processing of Gravity Gradients Data from GOCE[J]. Chinese Journal of Geophysics, 2012, 55(9): 2909-2916.

[24]徐新禹. 卫星重力梯度及卫星跟踪卫星数据确定地球重力场的研究[D]. 武汉: 武汉大学, 2008.

XU Xinyu. Study of Determing the Earth’s Gravity Field from Satellite Gravity Gradient and Satellite-to-satellite Tracking Data[D]. Wuhan: Wuhan University, 2008.

[25]钟波. 基于GOCE卫星重力测量技术确定地球重力场的研究[D]. 武汉: 武汉大学, 2010.

ZHONG Bo. Study on the Determination of the Earth’s Gravity Field from Satellite Gravimetry Mission GOCE[D]. Wuhan: Wuhan University, 2010.

[26]万晓云, 于锦海. 极地空白对GOCE引力场恢复的影响[J]. 测绘学报, 2013, 42(3): 317-322.

WAN Xiaoyun, YU Jinhai. Influence of Polar Gaps on Gravity Field Recovery Using GOCE Data[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 317-322.

[27]SCHUH W D. The Processing of Band-limited Measurements; Filtering Techniques in the Least Squares Context and in the Presence of Data Gaps[J]. Space Science Reviews, 2003, 108(1-2): 67-78.

(责任编辑：陈品馨)

修回日期： 2016-04-15

First author： MENG Xiangchao (1988—), male, PhD candidate, majors in GOCE gravity data processing and analysis.

E-mail： mxc20061115@163.com

E-mail： wxy191954@126.com

中图分类号：P228

文献标识码：A

文章编号：1001-1595(2016)07-0775-07

基金项目：国家自然科学基金(41404019；41274034)；国家863计划(2013AA122502-2)；大地测量与地球动力学国家重点实验室开放基金(SKLGED2014-3-5-E)

收稿日期：2016-01-13

第一作者简介：孟祥超(1988—)，男，博士生，研究方向为GOCE卫星重力数据处理与分析。

通信作者：万晓云

Corresponding author：WAN Xiaoyun

Optimization Method for Computing Radial Gravity Gradient Using Gravity Gradient Observations

MENG Xiangchao1,WAN Xiaoyun2,YU Jinhai1,ZHU Yongchao1,FENG Wei3,4

1. Key Laboratory of Computational Geodynamics, Chinese Academy of Sciences, Beijing 100049, China; 2. Qian Xuesen Laboratory of Space Technology, Beijing 100094, China; 3. Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China; 4. Beijing Satellite Navigation Center, Beijing 100049, China

Abstract：This paper proposes an optimization method for computing the radial gravity gradient by using GOCE gradient measurements, based on the variance-covariance information of gradient observations. The approach for computing the gravity gradient and the error propagation are firstly discussed; and then by solving a conditional extremum problem, we can get an optimal combination factor which can improve the calculation accuracy for the radial gravity gradient. The advantage of the combination factor is validated by simulation data. In actual data processing, the geoid accuracy truncated to degree 250 can be improved by 2 cm by using the optimization method. The radial gravity gradient can not only be used in recovering a gravity field model, but also can be used in kinds of geophysical interpretation, so the method provided in the paper can be helpful in the related researches.

Key words：GOCE; radial gravity gradient; optimization method; accuracy

引文格式：孟祥超, 万晓云，于锦海，等.利用引力梯度数据计算径向梯度的优化方法[J].测绘学报，2016,45(7)：775-781. DOI:10.11947/j.AGCS.2016.20160007.

MENG Xiangchao, WAN Xiaoyun,YU Jinhai,et al.Optimization Method for Computing Radial Gravity Gradient Using Gravity Gradient Observations[J]. Acta Geodaetica et Cartographica Sinica,2016,45(7):775-781. DOI:10.11947/j.AGCS.2016.20160007.