基于稀疏浮动车数据的城市路网交通流速度估计
2016-08-06王晓蒙池天河
王晓蒙,彭 玲,池天河
1. 中国科学院大学,北京100049; 2. 中国科学院遥感与数字地球研究所,北京 100101
基于稀疏浮动车数据的城市路网交通流速度估计
王晓蒙1,2,彭玲2,池天河2
1. 中国科学院大学,北京100049; 2. 中国科学院遥感与数字地球研究所,北京 100101
Foundation support: National Key Technology Support Program (No.2015BAJ02B00);Ministry of Science and Technology Policy Guidance Project (No.2011FU125Z24)
摘要:浮动车数据在时空维度呈现较强的稀疏性,是其应用于城市路网交通流估计所面临的主要难题之一。本文通过分析路网交通流速度的时空特征,构建了一种基于朴素贝叶斯法的估计模型,实现对路网中未被样本覆盖路段交通流速度的估计。时间特征主要考虑目标路段相邻时段的交通流速度,空间特征根据路段间交通流相似关系进行分析,突破了传统基于欧氏空间或拓扑关系的度量方式。结果显示,模型能有效地估计出样本缺失路段的交通流速度,且在精度方面相对传统基于拓扑关系的算法优势显著,较好地解决了数据时空稀疏性问题,对基于浮动车数据的交通应用具有较强的实践意义。
关键词:浮动车数据;稀疏性;交通估计;交通流相似关系
随着城市快速发展,出行需求急剧增加,交通拥堵成为北京、上海等大都市发展所面临的主要挑战之一。先进的城市交通流诱导是防止和减轻交通阻塞的有效手段,而交通状况实时信息采集是交通诱导系统的基础[1]。基于感应线圈、摄像头等固定传感器的静态交通流监测网络因其建设和维护成本高,难以覆盖整个城市路网[2]。近年来,浮动车数据(floating car data, FCD)以采集成本低、覆盖范围广等优点,逐渐成为一种重要的交通流信息来源。轨迹地图匹配[3-8]等数据预处理技术的发展,也为基于海量浮动车数据的交通流状态监测与分析创造了基础条件。
道路交通流包括流量、密度和平均速度等参数,它们之间密切相关,已有学者基于FCD对各种交通流参数的估计方法进行了研究[9-10]。其中,交通流平均速度是最常用的参数,包括时间平均速度(time mean speed,TMS)和空间平均速度(space mean speed,SMS)两种计算方式[11],基于FCD的交通流速度估计包括曲线拟合、轨迹追踪[12-13]以及基于流体动力学和排队理论的估计[14-15]等方法。
浮动车渗透率是影响交通流估计精度的主要因素之一,它代表车流中浮动车的比例,渗透率越高,基于浮动车数据的交通流估计精度越高,国内外学者针对不同类型道路探讨了保障估计精度情况下的最低渗透率[16-20]。
除了交通流估计方法和样本渗透率,若要将浮动车数据应用于全局城市路网的交通流检测,还需考虑由样本分布不均导致的时空稀疏性问题。目前,针对浮动车数据稀疏性问题的讨论较少,文献[21]通过历史数据估计缺失交通流状态,但这只考虑了交通流的周期性特征;文献[9]根据路网拓扑结构分析路段间交通流关系,从而估计未被传感器覆盖路段的交通流状况;文献[22]验证了交通流量数据在经过K-SVD方法训练过的字典上能够实现稀疏表达,文献[23]提出了一种基于压缩感知的估计算法,对交通流速度稀疏矩阵中的缺失项进行估计,然而该算法是基于全局时空范围的交通状况进行内部结构分析,只适用于离线应用。
为解决基于浮动车数据稀疏性问题,本文通过分析路网交通流速度时空特征,构建一种基于朴素贝叶斯法的估计模型,对路网中未被样本覆盖路段交通流速度进行估计。时间特征包括两个方面,一是路网交通状况随时间周期变化的特点,二是道路交通状况相邻时段间的转变特点。空间特征主要根据路段间的交通流空间关系进行分析,由于影响城市道路交通的因素复杂多元,路段间的交通流空间关系难以采用传统欧氏距离或拓扑关系的方式度量,因此,本文以大量动态数据为基础,实时地提取路段间交通流空间关系,也称作路段间交通流相似关系。
1缺失交通流速度估计
1.1路网交通流速度矩阵
本文主要考虑交通流速度参数,时空维度上的城市路网交通通过一个交通流速度矩阵表示
(1)
式中,连续时间被间隔Δt划分为t个离散的时间片段(简称“时段”);vrt表示路段r在t时段的交通流速度。由于本文主要关注样本缺失路段的交通流速度估计,为简化计算,直接经过目标路段浮动车的平均速度作为路段交通流速度,路段r在t时段的交通流速度通过式(2)计算
(2)
式中,为便于分析,vrt取值为1~100 km/h间的整数,当vrt超过100 km/h时,按100 km/h计算;vi为第i个样本速度;M为样本量,当M为0时,路段交通流速度缺失。本文主要目的就是对路网中缺失的交通流速度进行实时估计。
1.2路网交通流速度特征
1.2.1时间特征

1.2.2路段交通流相似关系
同一时段,路段交通状况的空间特征也是交通流速度估计的重要依据。在一些研究认为路段间交通状况符合邻近性原则,相邻路段的交通状况关系密切[9,24],然而,通过大量数据分析发现,这种假设并不准确。文献[25]根据路段交通流相似性进行路段划分,为路网交通特征分析提供了一种有效途径。本文在此基础上进行扩展,以大量历史浮动车数据为基础,对各时段路网的交通流进行分析,挖掘频繁出现的交通流相似关系,构建各路段的交通流相似集,用于样本缺失路段的交通流速度估计。所有与路段i的交通流特征相似度较高的路段形成的集合称为路段交通流相似集(简称“相似集”),可以表示为
(3)
式中,Si为路段i的相似集;R为路网所有路段集合;sij=1表示路段i和j交通流特征相似。一般可以通过聚类方法获取路网中所有路段的相似集,但城市路段数量庞大,传统聚类方法(例如k-mean聚类、谱聚类等)的矩阵运算开销巨大。为简化计算,本文先采用等量划分的方式对交通流速度进行初步分类,交通流速度所属类型可表示为
(4)
式中,vrt为路段r在t时段的交通流速度;Δv为划分间隔,Δv越小,分类越多,Δv最小值设置为1 km/h。由于不同等级的道路速度设计不同,有必要根据道路等级进一步分类,得到路网在t时段的交通流分类集合,并表示为
(5)
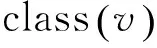
(6)
式中,Cdt表示第d天t时段的分类集合,需要针对每一列进行频繁模式挖掘,得到每个时段的频繁项集。通过一个指示函数表示集合c是否出现在C中

(7)
路段集c在D个工作日出现的频度记为freq
(8)
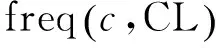


(9)

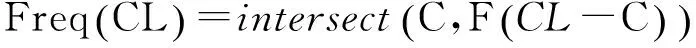

(11)
在交集和组合运算中,频度小的集合一定会包含频度高的集合,因此,在式(11)中,只需要考虑满足最小频繁度的最小元素个数[D·freqmin],则CL的频繁项集可以通过式(12)求得
(12)

1.3估计模型
将样本缺失路段的交通流速度估计看作多类分类问题,采用一种基于朴素贝叶斯法的估计模型。朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法[26]。将1.2节讨论的路网交通特征应用于模型的特征变量设计,输入特征包括前一时段路段交通流速度vp和当前时段目标路段相似集中路段的平均交通流速度vs,输出特征为路段当前时段的交通流速度v,3个速度特征取值为1~100 km/h间的整数,取值集合记为V。对路网每个时段的交通流相似关系都进行独立分析,当前时段的相似集与目标路段前一时段的交通流速度没有直接联系,因此,可以假设两个特征条件独立,则t时段特征间的条件概率公式为
(13)
(14)
将式(13)代入式(14),有
(15)
由于式(15)中分母对所有v都是相同的,所以t时段交通流速度的估计公式可以表示为
(16)
在初始时段,即t=1时,无法获取vp,此时假设模型只有一个输入特征vs,则最终的估计公式为
(17)
对于参数学习,贝叶斯估计对极大似然估计进行改进,避免估计的概率值为0的情况。条件概率的贝叶斯估计为
(18)
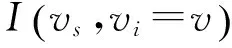
(19)
2试验结果
2.1数据状况
研究空间范围为北京市六环以内区域,覆盖路段约12万条,包括快速路、主干路、次干路和支路等。时间区间为6:00—24:00,被Δt=10 min划分为108个时段。浮动车样本采用北京市2012年出租车轨迹数据,记录了约1.2万辆出租车一个月内的运行状态,包括时间、位置、航向角、车速等信息,样本总量约8亿条,采样间隔为1~120 s。设路段样本覆盖率为x/108,其中,x为目标路段被样本覆盖的时段数,统计结果显示,快速路样本覆盖率为42.57%,主干路样本覆盖率为57.26%,次干路样本覆盖率为34.77%,而支路和街坊路的样本覆盖率不足10%(如图2所示)。由此可见,样本稀疏性是基于浮动车数据进行路网交通流速度估计亟待解决的难题。

图1 工作日路网整体平均运行速度Fig.1 Average speeds of road network on weekdays

图2 路网样本覆盖率空间分布情况Fig.2 Sample space distribution of floating car data
2.2模型实现
模型实现包括相似集挖掘和参数估计两部分,为方便观察,从路网中筛选出样本覆盖情况较好的16 469路段,确保每天的样本分类都能找到所有的路段。选取5个连续工作日的历史数据进行模型学习,频繁项的最小频度freqmin设置为80%。为平衡相似集精度与覆盖率之间的关系,进行分类和频繁模式挖掘时,采取5个分类策略,Δv分别设置为1~5km/h的整数。分类时划分间隔Δv越小,分类精度越高,但分类对于路段的覆盖率越低,如图3所示,采用1km/h进行分类时,相似集路段覆盖率在13.58%~25.89%之间,而采用5km/h,覆盖率在88.96%~100%之间,这5种分类策略的协同应用基本满足模型的需求。

图3 不同分类策略下相似集对路段覆盖率Fig.3 Coverage rates of similarity set under different classification policy

图4 各时段交通流速度概率分布Fig.4 Probability distribution of traffic speed at each time slot
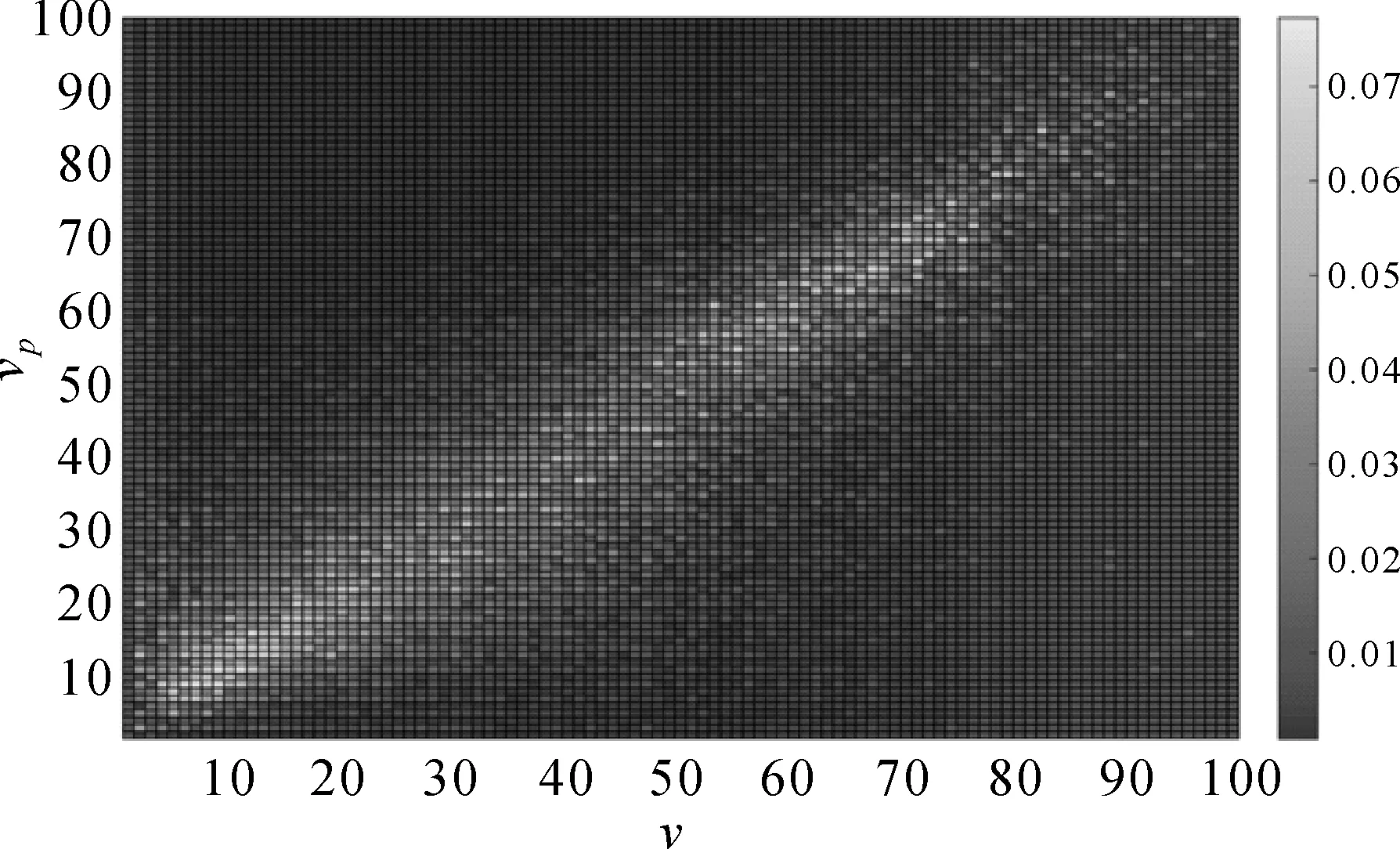
图5 分布第12时段分布Fig.5 Distrbution of Pt(vp|v)at 12th time slot

图6 第12时段Pt(vs|v)分布Fig.6 Distribution of Pt(vs|v)at 12th time slot
2.3模型应用效果
筛选部分路段进行试验,按照2.1节的方式统计,目标路段集合的整体样本覆盖率为58.78%,每个路段的有效样本覆盖率分布情况如图7所示。
估计结果显示,模型能估计出92.55%的缺失状态,使路网交通状况覆盖率达到96.93%,每个路段的覆盖率分布情况如图8所示,绝大多数路段交通状况覆盖率达到90%以上。
将估计前和估计后的交通流速度分布图(图9、10)对比观察,估计前,路网中大量路段没有被样本覆盖,估计后,路网交通流状况分布图能够反映出清晰的实时交通流速度,只存在极少数状态缺失的路段,能更好地应用于交通系统。

图7 估计前样本覆盖率Fig.7 Sample coverage rate before estimation
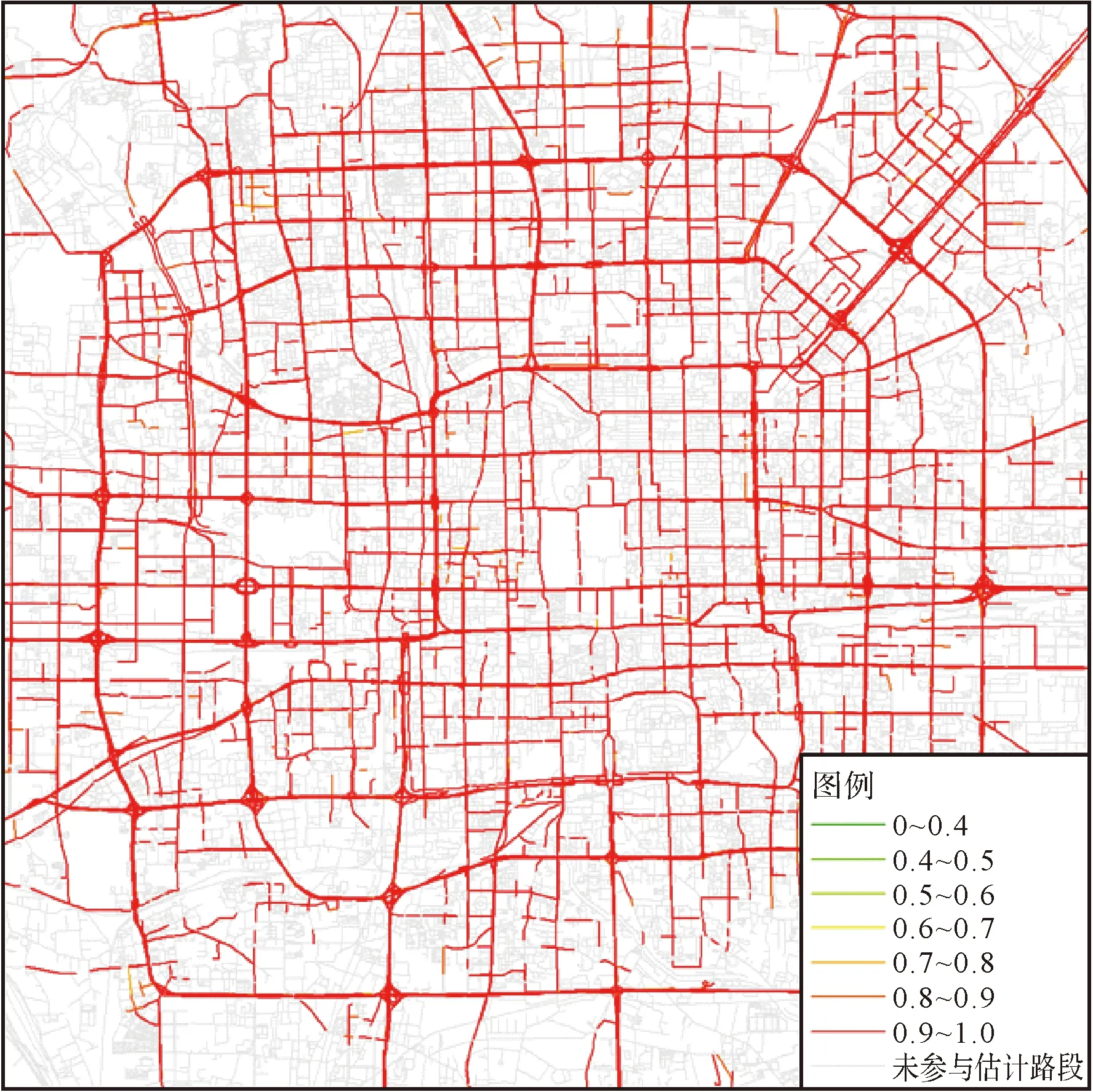
图8 估计后交通状况覆盖率Fig.8 Sample coverage rate after estimation
排除原样本缺失情况,以有效样本为基础,从中随机剔除部分样本,形成覆盖率为10%~90%的多个试验用例。对比估计前后交通状况覆盖率,结果如图11所示,当原始样本覆盖率只有40%时,估计后的交通状况覆盖率还能达到90%以上,说明模型能有效地估计出样本缺失路段的交通流速度。

图9 估计前第12时段交通流速度Fig.9 Traffic state before estimation
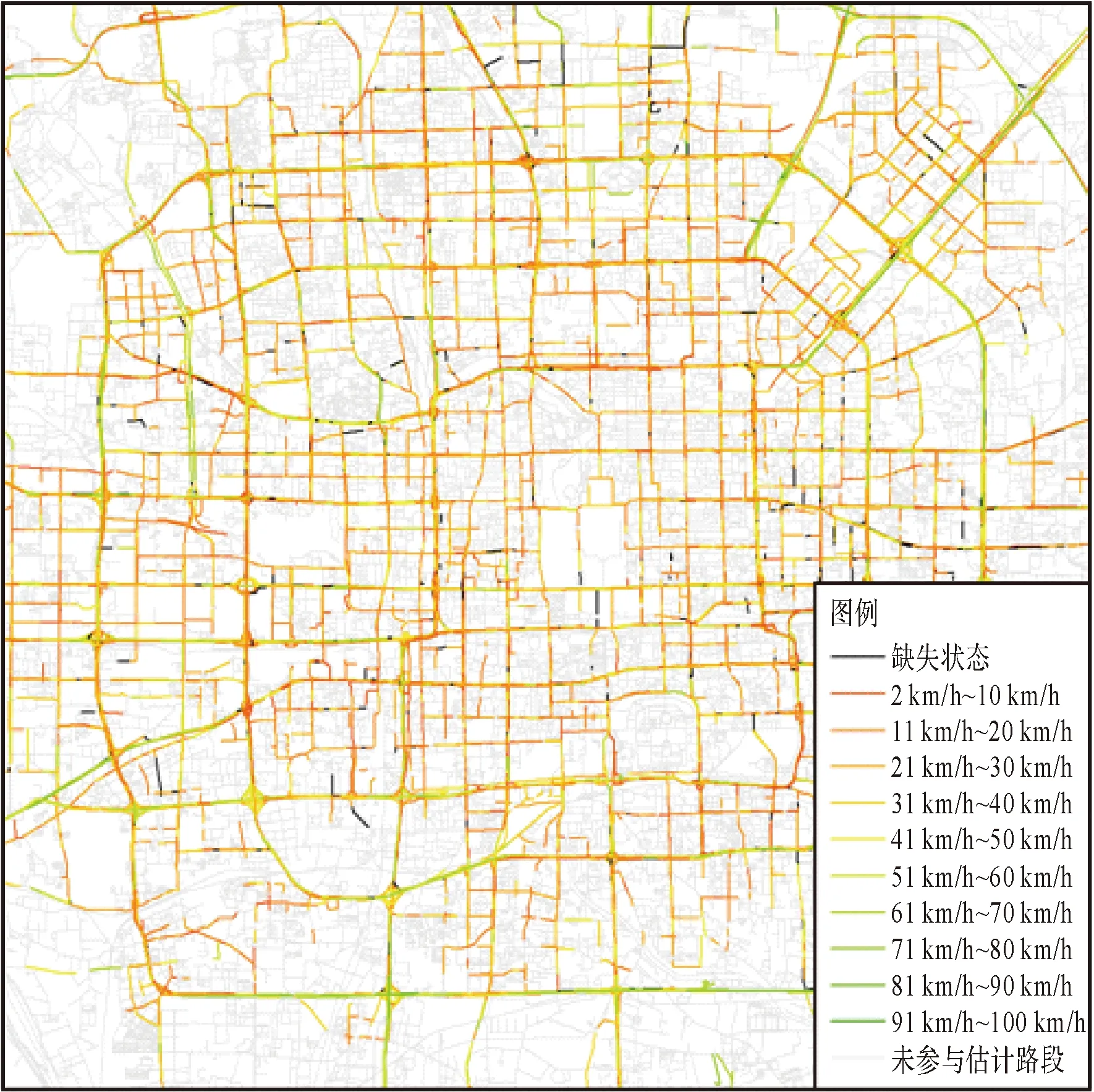
图10 估计后第12时段交通流速度Fig.10 Traffic state before estimation
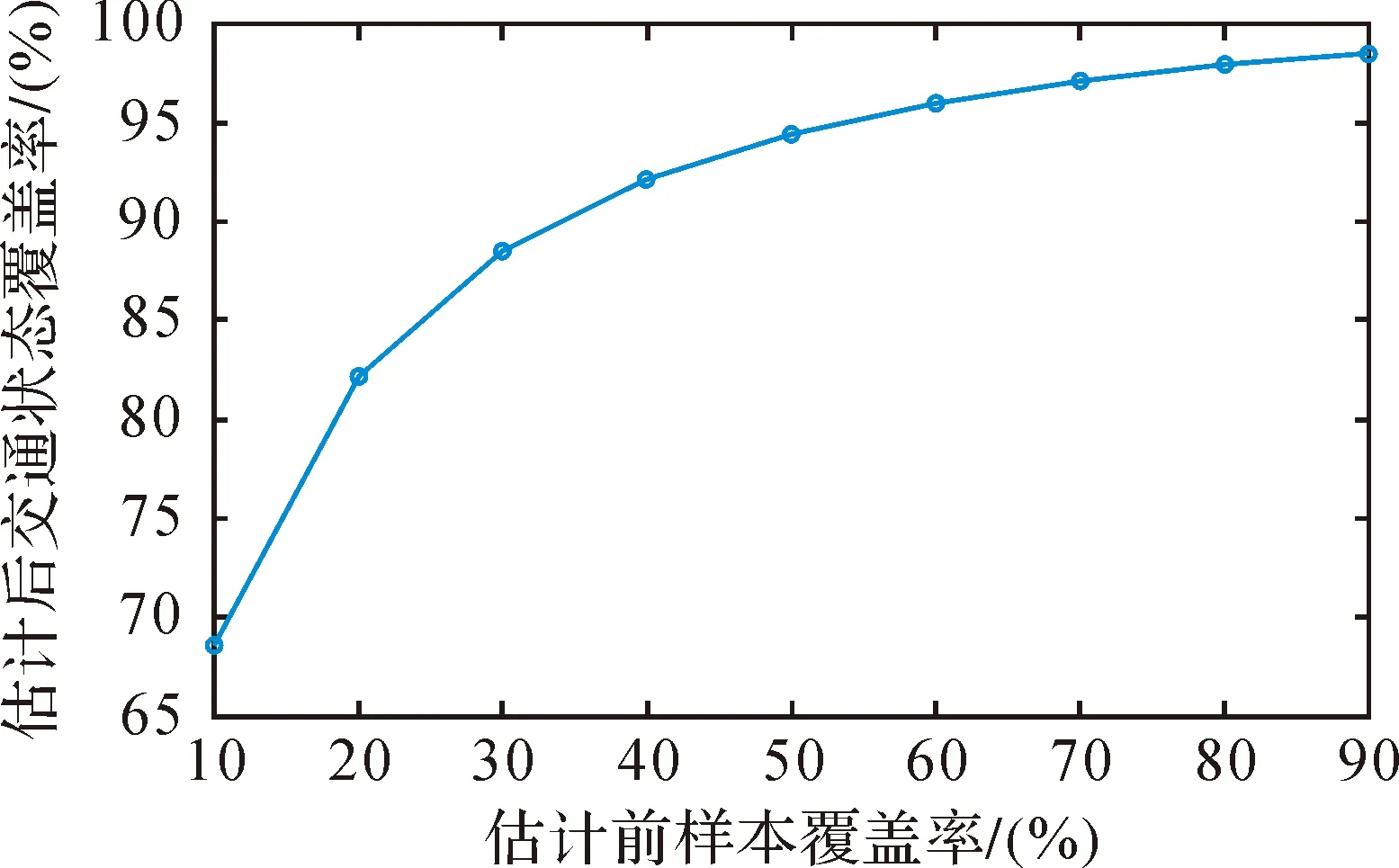
图11 估计前后交通流状况覆盖率关系Fig.11 Relationship of the coverage rates between ex-ante and ex-post estimations
试验对两种模型对比分析,模型1为2.3节提出的模型,模型2采用路段间的拓扑关系设计特征变量,将模型1中的vs替换为目标路段相邻路段集合对应的平均交通流速度va,va根据加权平均计算
(20)


图12 两种模型估计精度对比Fig.12 Comparison of accuracy between the two models
3结论
浮动车数据各路段各时段的样本分布不均,有较强的时空稀疏性,在实际应用中需要对样本缺失路段的交通流状况进行估计。本文构建了基于朴素贝叶斯法的交通估计模型,实现对样本缺失路段交通流速度的实时估计,模型参数设计主要依据路网交通流速度的时间特征以及路段间交通流相似关系。试验结果表明,模型能有效地估计出样本缺失路段的交通流速度,在样本覆盖率只有40%的情况下,还能使估计结果中的交通状况覆盖率达到90%;在与基于拓扑关系的估计算法对比中,基于交通流相似关系的模型估计精度较高,进一步说明,相对传统的欧氏距离和拓扑关系,基于海量数据挖掘的路网交通流相似关系能更准确地表达路段间交通流空间关系;另外,基于朴素贝叶斯法的估计模型算法复杂度较低,运算效率较高,适用于实时交通应用。
参考文献:
[1]孙棣华, 董均宇, 廖孝勇. 基于GPS探测车的道路交通状态估计技术[J]. 计算机应用研究, 2007(2): 243-245, 248.SUNDihua,DONGJunyu,LIAOXiaoyong.TrafficParameterEstimationBasedonGPSEquippedProbeVehicles[J].ApplicationResearchofComputers, 2007(2): 243-245, 248.
[2]HERRERA J C, BAYEN A M. Traffic Flow Reconstruction Using Mobile Sensors and Loop Detector Data[C]∥Proceedings of the TRB 87th Annual Meeting Compendium of Papers DVD. Washington, DC: Transportation Research Board, 2007.
[3]王美玲, 程林. 浮动车地图匹配算法研究[J]. 测绘学报, 2012, 41(1): 133-138.
WANG Meiling, CHENG Lin. Study on Map-matching Algorithm for Floating Car[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 133-138.
[4]唐进君, 刘芳. 基于路径预测的不确定性推理组合地图匹配算法[J]. 测绘学报, 2010, 39(5): 546-550.
TANG Jinjun, LIU Fang. A Driver Route Prediction Based Map-matching Algorithm Integrating Uncertain Reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 546-550.
[5]李清泉, 黄练. 基于GPS轨迹数据的地图匹配算法[J]. 测绘学报, 2010, 39(2): 207-212.
LI Qingquan, HUANG Lian. A Map Matching Algorithm for GPS Tracking Data[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 207-212.
[6]唐进君, 曹凯. 一种自适应轨迹曲线地图匹配算法[J]. 测绘学报, 2008, 37(3): 308-315.
TANG Jinjun, CAO Kai. An Adaptive Trajectory Curves Map-matching Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 308-315.
[7]苏洁, 周东方, 岳春生. GPS车辆导航中的实时地图匹配算法[J]. 测绘学报, 2001, 30(3): 252-256.
SU Jie, ZHOU Dongfang, YUE Chunsheng. Real-time Map-matching Algorithm in GPS Navigation System for Vehicles[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(3): 252-256.
[8]王晓蒙, 池天河, 林晖, 等. 一种面向海量浮动车数据的地图匹配方法[J]. 地球信息科学学报, 2015, 17(10): 1143-1151. WANG Xiaomeng, CHI Tianhe, LIN Hui, et al. A Research of Map-matching Method for Massive Floating Car Data[J]. Journal of Geo-information Science, 2015, 17(10): 1143-1151.
[9]FOWE A J, CHAN Yupo. A Microstate Spatial-inference Model for Network-traffic Estimation[J]. Transportation Research Part C: Emerging Technologies, 2013, 36: 245-260.
[10]DARWISH T, ABU BAKAR K. Traffic Density Estimation in Vehicular ad Hoc Networks: A Review[J]. Ad Hoc Networks, 2015, 24: 337-351.
[11]VAN LINT J W C. Reliable Travel Time Prediction for Freeways[D]. Delft: Delft University of Technology, 2004.
[12]KONG Qingjie, ZHAO Qiankun, WEI Chao, et al. Efficient Traffic State Estimation for Large-scale Urban Road Networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(1): 398-407.
[13]BEJAN A I, GIBBENS R J. Evaluation of Velocity Fields via Sparse Bus Probe Data in Urban Areas[C]∥Proceedings of the 2011 14th International IEEE Conference on Intelligent Transportation Systems (ITSC). Washington, DC: IEEE, 2011: 746-753.
[14]HIRIBARREN G, HERRERA J C. Real Time Traffic States Estimation on Arterials Based on Trajectory Data[J]. Transportation Research Part B: Methodological, 2014, 69: 19-30.
[15]CAO Peng, MIWA T, MORIKAWA T. Use of Probe Vehicle Data to Determine Joint Probability Distributions of Vehicle Location and Speed on an Arterial Road[J]. Transportation Research Record, 2014, 2421: 103-114.
[16]HERRERA J C, WORK D B, HERRING R, et al. Evaluation of Traffic Data Obtained via GPS-enabled Mobile Phones: The Mobile Century Field Experiment[J]. Transportation Research Part C: Emerging Technologies, 2010, 18(4): 568-583.
[17]DE FABRITIIS C, RAGONA R, VALENTI G. Traffic Estimation and Prediction Based on Real Time Floating Car Data[C]∥Proceedings of the 2008 11th International IEEE Conference on Intelligent Transportation Systems. Beijing: IEEE, 2008: 197-203.
[18]BAR-GERA H. Evaluation of a Cellular Phone-based System for Measurements of Traffic Speeds and Travel Times: A Case Study from Israel[J]. Transportation Research Part C: Emerging Technologies, 2007, 15(6): 380-391.
[19]BREITENBERGER S,GRUEBER B,NEUHERZ M,et al. Traffic Information Potential and Necessary Penetration Rates[J]. Traffic Engineering & Control, 2004, 45(11): 396-401.
[20]WANG Handong, YUE Yang, LI Qingquan. How Many Probe Vehicles Are Enough for Identifying Traffic Congestion?—A Study from a Streaming Data Perspective[J]. Frontiers of Earth Science, 2013, 7(1): 34-42.
[21]WANG Jiawei, WANG Yinsong, YUN Meiping, et al. Development of Urban Road Network Traffic State Dynamic Estimation Method[J]. Mathematical Problems in Engineering, 2015, 2015: 714149.
[22]李清泉, 周尧, 乐阳, 等. 基于压缩传感的交通流量数据压缩方法[J]. 交通运输工程学报, 2012, 12(3): 113-119, 126. LI Qingquan, ZHOU Yao, YUE Yang, et al. Compression Method of Traffic Flow Data Based on Compressed Sensing[J]. Journal of Traffic and Transportation Engineering, 2012, 12(3): 113-119, 126.
[23]ZHU Yanmin, LI Zhi, ZHU Hongzi, et al. A Compressive Sensing Approach to Urban Traffic Estimation with Probe Vehicles[J]. IEEE Transactions on Mobile Computing, 2013, 12(11): 2289-2302.
[24]HOFLEITNER A, HERRING R, ABBEEL P, et al. Learning the Dynamics of Arterial Traffic from Probe Data Using a Dynamic Bayesian Network[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(4): 1679-1693.
[25]张心哲, 关伟. 基于聚类分析的城市交通路段划分研究[J]. 交通运输系统工程与信息, 2009, 9(3): 36-42.
ZHANG Xinzhe, GUAN Wei. Division of Urban Traffic Road Section Based on Clustering Analysis[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(3): 36-42.
[26]李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012: 47-53. LI Hang. Statistical Learning Method[M]. Beijing: Tsinghua University Press, 2012: 47-53.
(责任编辑:宋启凡)
修回日期: 2016-01-08
First author: WANG Xiaomeng (1986—), male, PhD, majors in cartography, GIS and smart city.
E-mail: wangxiaomeng1986@163.com
E-mail: plqiqi@126.com
中图分类号:P208
文献标识码:A
文章编号:1001-1595(2016)07-0866-08
基金项目:国家科技支撑计划(2015BAJ02B00);国家科技部政策引导类项目(2011FU125Z24)
收稿日期:2015-09-15
第一作者简介:王晓蒙(1986—),男,博士,研究方向为地图学与地理信息系统、智慧城市。
通信作者:彭玲
Corresponding author:PENG Ling
A Method of Urban Traffic Flow Speed Estimation Using Sparse Floating Car Data
WANG Xiaomeng1,2,PENG Ling2, CHI Tianhe2
1. University of Chinese Academy of Sciences, Beijing 100049, China; 2. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China
Abstract:The sample spatio-temporalsparsity is one of the major challenges for traffic estimation when using floating car data (FCD).Spatio-temporal characteristics of road traffic flow are analysed and applied to build a naive Bayes-based traffic estimation model which is proposed to estimate the missing traffic state of the roads which are not covered by samples. In the model, the adjacent period traffic flow speed of the target road segment is considered for the representation of the time characteristic. And instead of Euclidean distance and topology relationship, urban traffic flow similarity relationships are mined to quantify the interior space features of urban traffic.The result demonstrates that the method is effective for missing traffic state estimation and more precision compared to traditional methods based on topology relationship.As a conclusion, the proposed model can solve the spatio-temporal sparsity problem effectively, which has a strong practical significance for traffic application based on FCD.
Key words:floating car data (FCD); sparsity; traffic estimation; traffic flow similarity relationship
引文格式:王晓蒙,彭玲,池天河.基于稀疏浮动车数据的城市路网交通流速度估计[J].测绘学报,2016,45(7):866-873. DOI:10.11947/j.AGCS.2016.20150472.
WANG Xiaomeng,PENG Ling, CHI Tianhe.A Method of Urban Traffic Flow Speed Estimation Using Sparse Floating Car Data[J]. Acta Geodaetica et Cartographica Sinica,2016,45(7):866-873. DOI:10.11947/j.AGCS.2016.20150472.
