地图信息论：从狭义到广义的发展回顾

李志林，刘启亮，高培超

1. 西南交通大学高铁运营安全空间信息国家地方联合工程实验室，四川 成都 611756； 2. 香港理工大学土地测量与地理资讯学系，香港 九龙； 3. 中南大学地理信息系，湖南 长沙 410083



地图信息论：从狭义到广义的发展回顾

李志林1,2，刘启亮2,3，高培超2

1. 西南交通大学高铁运营安全空间信息国家地方联合工程实验室，四川 成都 611756； 2. 香港理工大学土地测量与地理资讯学系，香港 九龙； 3. 中南大学地理信息系，湖南 长沙 410083

Foundation support： The National Basic Research Program of China(973 Program)(No.2012CB719901)；The National Natural Science Foundation of China(No.41471383)；Hong Kong General Research Fund(No.B-Q49E)

摘要：地图是人类认识客观世界的有力工具。地图的核心功能是传输空间信息。自20世纪60年代源自通信领域的信息论被引入地图信息度量，现代地图学已经发展了一个崭新的研究领域——地图信息论。本文旨在对近50年来地图信息论的发展历程进行回顾，论述从狭义到广义地图信息论的基本概念、研究进展及应用领域，最后对地图信息论的发展进行了展望。

关键词：地图学；信息论；地图信息论；狭义地图信息论；广义地图信息论

地图被认为是人类最古老的3大交流工具之一，是空间信息传输的主要工具。地图负载了丰富的自然、人文、社会、经济等信息，是改变世界的十大地理思想之一。地图作为人类社会发展所不可或缺的重要媒介，在人类文明史上具有重要的地位。

地图学的研究，也像其他学科一样，从物质流、能量流和信息流等3大方面进行。这3种流贯穿地图学的整个过程，但在各个阶段侧重有所不同。传统的地图制作(从数据采集到地图绘制)主要是物质流，尽管也有信息流部分。在地图的解译和使用阶段，起主导作用的是地图能量流，尽管也有信息流和物质流部分。地图的能量指的是对人们的思想与决策行为的影响，因为“地图所赋予我们的现实超出我们的视野、我们的掌握、我们的时间，那是一种我们别无他法可以获得的现实”[1]。阐述能量流的典型著作包括《地图的力量》[1]及《地图的本质》[2]。信息流的研究源自20世纪50年代，早期研究方法主要是模拟自然语言的交流过程，即作者-读者之间的信息传输，而地图被视为两者之间的介质[3-4]。在20世纪60年代，地图学界将香农(Shannon)的信息传输理论[5]引入地图学领域[6]，试图建立基于现代信息论的地图信息论。

经过近50年的发展，地图信息论已经成为现代地图学的一个核心研究领域，国内外学者针对地图信息量计算这一核心目标已经开展了大量的研究工作，并取得了可喜的研究成果。本文旨在对近半个世纪以来，地图信息论的发展历程进行梳理，从狭义地图信息到广义地图信息度量的研究脉络对当前研究的进展进行回顾和总结，并对地图信息论研究存在的问题与发展方向进行探讨。

1香农信息论与地图信息论

20世纪40年代末以来，信息量的度量首先在通信领域取得突破，美国科学家香农首先基于概率与统计思想提出了信源不确定性的度量指标——信息熵，奠定了现代信息论的基础[5]。1967年Sukhov率先将信息论引入地图学领域，提出了用于度量地图符号多样性的信息熵度量指标[6]，开启了地图信息论。

1.1香农信息熵与信息论

信息的定义是信息度量的前提，信息论的创始人香农把信息的定义为“信息是事物运动状态或存在方式的不确定性”。信息量是对信息统计特征的一种描述，香农从统计上给出了信息传输模型中(图1)信息量的计算方法。

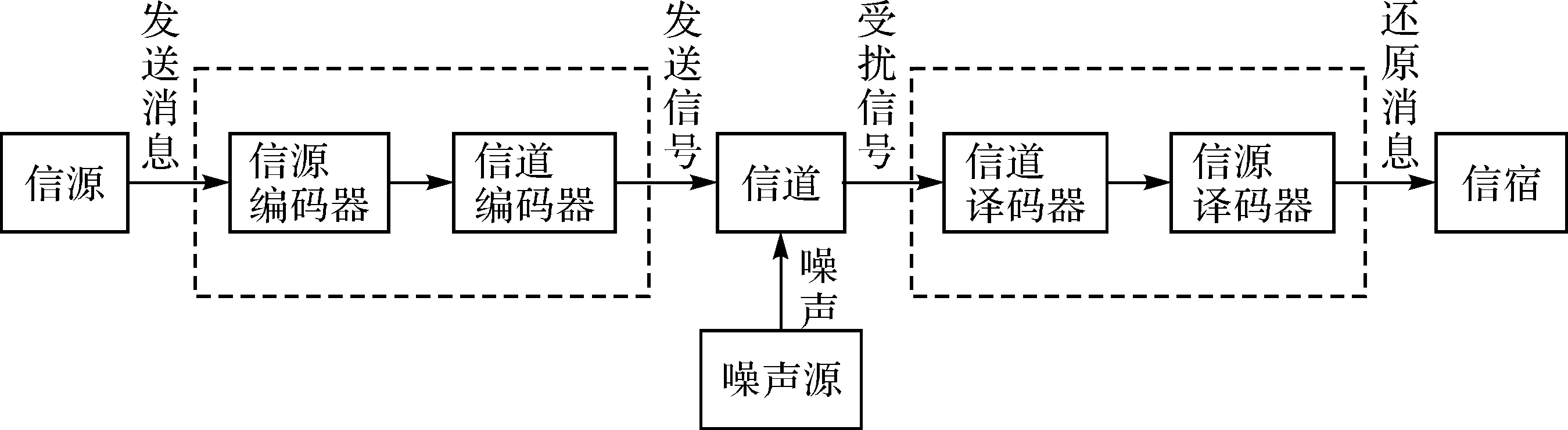
图1　信息传输模型 (http:∥wiki.mbalib.com/wiki/Information_theory)Fig.1　The model of information transmission(http:∥wiki.mbalib.com/wiki/Information_theory)

信息熵：表示了信源所包含的平均信息量，它表征了信源输出后每个消息提供的平均信息量(或信源输出前的平均不确定度)，定义为

(1)

式中，P(xi)表示随机变量X每一个可能取值xi的概率。

互信息：设X为信源，Y为信宿，I(X;Y)表示信道传输的平均信息量，定义为

I(X;Y)=H(X)+H(Y)-H(X,Y)

(2)

(3)

式中，H(X,Y)表示联合熵，代表了通信前后整个系统仍存在的不确定度；P(xy)表示事件x、y同时发生的概率，即联合概率。

条件熵：条件熵H(X|Y)表示给定随机变量Y时，随机变量X的平均不确定性，它表征了因信道干扰所损失的平均信息量；H(Y|X)表征了因信道干扰产生的噪声熵，分别定义为

(4)

(5)

上述公式表达了信号从信源到信宿的传输过程中的各种信息量，其关系如图2所示。

图2　信息传输过程中各种信息量间的关系(改自文献[7])Fig.2　The relationship among different entropy in information transmission[7]

信息论：香农把热力学的思想创造性地引入了信息学领域，建立了以信息熵为基础的信息传输理论-信息论。信息论运用概率论与数理统计的方法研究信息、信息熵、通信系统、数据传输、密码学、数据压缩等问题，是信息科学领域第一次脱离物理层面，仅仅只在数学层面完成自洽，并且在数学层面验证了数据传输的极限和压缩率的极限[8]。

1.2地图统计信息熵的定义：狭义地图信息论的兴起

自香农创建了信息论后，地图学界试图将信息论引入，建立一套地图信息传输理论。美国的Robinson教授等学者在20世纪50年代就开始在努力，提出了多个地图信息传输模型[3]。图3是由捷克地图学家Kolacny提出的一个代表性模型[9]，可以看出，这仅仅是模仿图1信息传输模型的概念模型。

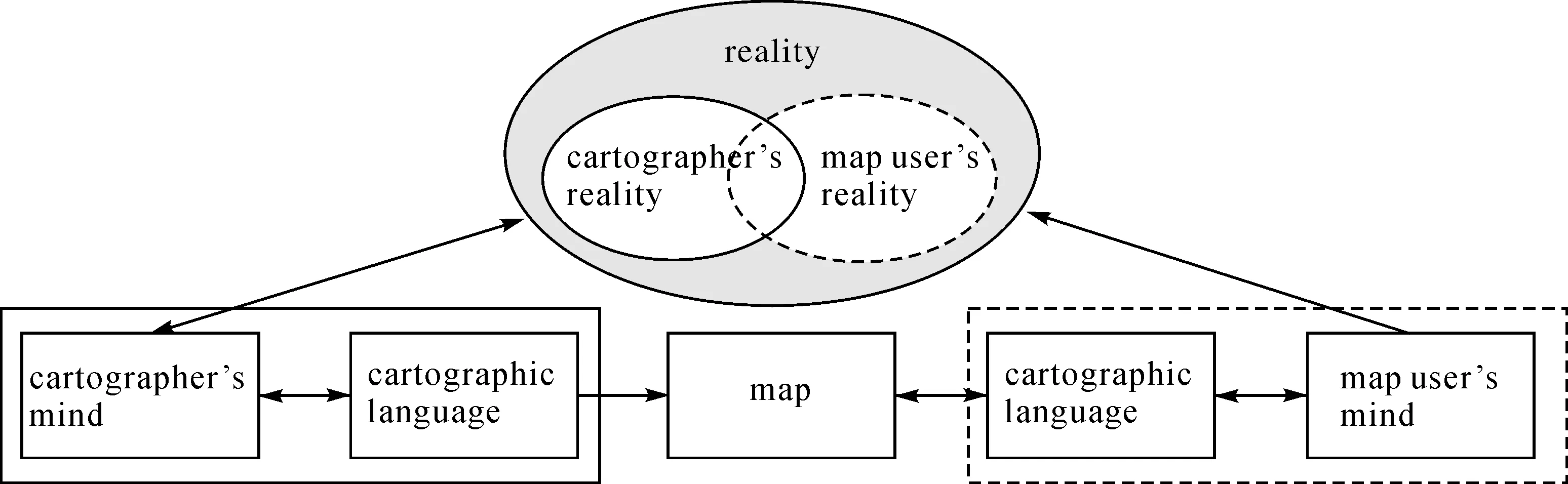
图3　捷克地图学家Kolacny教授提出的地图信息传输模型[9]Fig.3　The cartographic information transmission model proposed by Kolacny[9]

要建立地图信息传输理论，必须建立一套数学模型。为此，前苏联制图学家Sukhov教授率先将香农的信息熵引入地图学[6]，对地图信息进行度量。假设，N为地图上所以符号得总数，M为地图上符号的总类数，第i类符号的数量为Ki，则地图上每类符号的频率为

(6)

将式(6)代入式(1)，即可算出该地图的信息量。地图学界早期大部分的工作是通过计算频数的方式直接套用信息熵的计算公式，即式(1)。例如，计算地图上居民地行政分级、人口分级与汉字出现频率对居民地要素信息量进行度量[10]；计算坐标、数字(字母)出现频次对地图上地物的位置和注记信息进行度量[11]；计算每个地图符号的邻接度的频数得到拓扑关系的概率，用于计算地图的拓扑信息熵[12]。

这种基于地图符号频率的信息熵实际上是统计信息熵，本文将基于这种统计信息熵的地图信息传输理论称为狭义地图信息论，因为地图不仅包含统计信息，更重要的是包含各种空间信息。目前，狭义地图信息论在地图综合[13]和地图设计等方面得到普遍应用[14]。

1.3地图统计信息熵的先天不足：狭义地图信息论的局限性

引入信息论对地图信息进行度量使得地图负载信息的计算更为科学，然而基于概率频次的地图信息量计算方法到底反映了何种地图信息需要仔细分析。地图作为一种图形语言，从认识论的层次上，地图信息可以被划分为3个层次：语法地图信息、语义地图信息及语用地图信息[15-16]。语法地图信息表征了地图上地物或现象的时空状态与组合存在方式；语义地图信息表征了地物或现象的时空状态与组合存在方式的含义；语用地图信息表征了具有特定含义的时空状态和存在方式对地图用户的价值和效用。香农本人已经隐含地表明其探讨的信息熵仅仅是在语法层次[17]，因此以Sukhov提出的符号信息熵为代表的地图信息度量亦在语法地图信息的范畴。进而，需要探讨这种统计信息熵是否能够有效度量语法地图信息。

图4　地图的统计信息量例子Fig.4　Examples of the statistical information of maps

图5　两幅各类符号数量完全相同，但分布于不同的地图[18])Fig.5　Two maps with same symbols, but different spatial distributions[18]

2地图信息论：从狭义到广义

伴随着地图信息论研究的深入，国内外学者逐渐认识到狭义地图信息论度量地图信息量的不足，并逐渐从地图信息的来源与特点出发对地图信息进行度量[18]。

2.1地图空间信息量的定义：广义地图信息论的开启

文献[18]对地图信息进行深入的剖析，认为除了统计信息外，地图信息更重要的应包括：

(1) 几何信息，包括了地图要素的位置、数量、大小与形状等信息。

(2) 空间关系信息，包括了地图要素拓扑、方向、距离及分布等信息。

(3) 专题信息，包括了地图要素的类型、重要程度等信息。

他们借助V(Voronoi)图，将离散的地图要素有机地关联起来(图6)，“运用了Voronoi图对地图要素占用区域划分的思想，克服了经典信息论对地图仅进行简单统计学度量的局限性，使得几何信息这一地图的重要特性有了明确的数学度量方法”[19]。他们“针对地图要素提出了通过建立Voronoi图来量测地图的几何信息量、专题信息量和拓扑信息量的方法, 使得地图学中的信息量量测有了新的方法”[20]。

图6　基于V(Voronoi)图的地图几何信息量计算[18]Fig.6　The calculation of metric information based on Voronoi diagram[18]

2.1.1地图几何信息量(metric information)

设一幅地图上有N个符号，每个地图符号的V图所占面积与整个地图区域面积的比率为

Pi=Si/Si=1,2,…,N

(7)

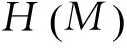
(8)

图5中两幅地图的几何信息熵分别为4.29和5.13(图6)，即右图的信息熵高于左图。当两幅包含不同符号数量地图的几何信息量时，进一步给出了地图几何信息量的标准化形式

(9)

式中，Hmax(M)表示当所有地图符号的V图面积均相同时取得的最大熵，Hmax(M)=log2N。

2.1.2地图专题信息量(thematic information)

设第i个地图符号有Ni一阶邻近符号(图7(a))，这些邻近符号具有Mi种专题类型，其中第j种专题类型的符号个数为Ni，则第i个邻居符号包含第j种专题属性类型的频率定义为

(10)

图7　基于Voronoi图的地图专题信息量计算Fig.7　The calculation of thematic information based on Voronoi diagram[18]

图7(b)是对这些数学符号的解释。将式(10)代入信息熵公式中可获得每个符号的专题信息量，累加后可计算整幅地图的专题信息量。整幅地图信息熵的完整数学表达式为

(11)

2.1.3地图拓扑信息量(topological information)

每个地图符号V图的一阶邻居数目的平均值用来表征拓扑关系的信息量。

文献[18]给出的地图信息量分类体系与计算指标将信息论与地图信息有机融合，将单纯的统计信息量拓展为真正意义上的地图信息量，其满足了地图信息度量的两个核心原则：①地图符号的空间分布不同，地图空间信息量就不同；②有地图符号就有空间信息量。

学者们发现这种基于的 V图空间信息度量一方面反映了地图实体对空间占有的势力划分，另一方面也体现出地物之间的邻接关系, 而这两方面正是语法层次地图信息量的主要体现[20-21]。亦有文献[18]认为“基于Voronoi图的几何度量方法是现有的对地图信息的最佳量测, 其将地图学的具体问题与信息论基本原理结合的方法是符合地图信息度量具体实践的”[22]。

2.2对文献[18]地图空间信息度量扩展的种种尝试

对文献[18]的地图空间信息度量，有些学者认为仅考虑V图的面积比不够,应该将面积比或其他度量指标分类(分段)，再算每类(段)的频率[7]。然而，这种做法不但忽略了类别区别(因为不同类别的符号也会可能有相同的V图面积)，也忽略了符号空间位置区别(每个符号与其他都有位置区别)，计算的结果既不是统计信息熵，也不能满足“有地图符号就有空间信息”的基本原则。

也有些学者认为，当符号的空间分布趋近均匀时，文献[18]的地图几何信息量最大，这跟香农的“概率小、信息量大”相反[23]。事实上，“概率小信息量大”是指单个事件，而香农的总信息熵就是在概率相同时出现最大值，因为均匀分布意味着大离散度，就产生大信息熵。

对文献[18]的地图空间信息度量，国内外许多学者作了种种扩展的尝试，这里进行简单回顾。

3.2.1基于加权V图量测多级地图要素几何信息量

有学者认为V图具有势力范围属性特性，这与地理信息的空间范围性表现出很好的一致性，地物空间范围性不仅反映了地理事物所处的位置、尺寸，更重要的是它间接反映了地理事物之间的关系,因此基于V图来量算地图几何信息量从方法论角度基本解决了地图几何信息的度量问题[19]。但是，文献[18]的度量没有引入级别的概念，即没有考虑地物要素的多级别性，因此需要对不同级别地物加以权重来计算的V图

(12)

式中，Ri是第i级别符号的几何度量。

图8表示从等权的V图(左图)到加权后V图的变化。他们的结论是：考虑不同类别的固有特征, 具有地理学上的有用性。这一扩展很有意义，但可能需要弄清楚是在哪个层次上的扩展，即“不同类别的固有特征”可能与语义有关，而“地理学上的有用性”可能与语用有关。

图8　顾及地图要素级别的加权V图Fig.8　Use of weighted Voronoi diagram with consideration of map element levels

2.2.2基于符号大小及符号V图面积差异的几何信息量

一些学者试图对几何信息量度量进行修正，如几何信息量与符号大小关联[24](式13)、与V图的面积差异关联[25](式14)。几何信息量与符号大小关联计算的方法如式(13)所示

(13)

式中，S为总符号面积；Si表示第i个地图符号的面积。这样就可以发现，当两幅地图同样两个符号(如房子和三角点)，当三角点符号变小时，地图的信息熵变小，但信息量跟符号的空间分布(特别是邻接关系)无关。

图9　同样两个符号，大小不一样，信息量也不一样Fig.9　Different information for two symbols with the same type but different sizes

用V图的面积差异来定义地图空间信息的公式如式(14)所示

(14)

式中，Si为第i个符号的V图面积；Sav为符号的V图的平均面积；Smax为最大的V图的面积。可以发现，这样的定义会出现奇怪现象，即“有符号没信息”及“两符号的V图面积很不一样而信息量却一样”。图10表达了这种情况。左图中，Si=Sav=Smax，因此信息量为0。右图中，Sav=1/2，Smax=2/3，S1=1/3，S2=2/3，所以两个符号的信息量是一样的，尽管一个的V图面积是另一个的2倍。这类研究实际上是从方差的角度对于地形图信息进行了度量，由于方差与信息量存在正相关的关系，因此可以在一定程度上反映地形图的统计分布信息，但是将方差替代信息计算中的概率缺乏严密的理论依据，而且不满足地图信息度量的基本原则(有符号但无信息)。

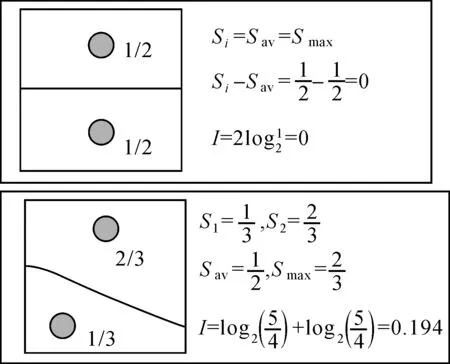
图10　两种奇怪现象：有符号没信息及两符号的V图面积很不一样而信息量一样Fig.10　Two examples: a map with symbols but without information; two symbols with different sizes of Voronoi regions with same information

2.2.3基于邻近像素灰度值差的信息度量

有学者认为，地图符号的信息跟符号的吸引力(attractiveness)有关，并提出了一种基于像素邻近灰度值之差的信息度量方法，即信息量是所考虑的像素(P)与周边像素灰度值差的总和[26]

(15)

式中，Cp是所考虑的像素的灰度值；Ci是第i个邻近像素的灰度值；m是邻近像素的个数，在一个3×3的窗口时为8(图11(a))；ki为一个常数。一幅影像的信息量为所像素的信息的总和，如果地图是彩色的，则将色彩分解成RGB分别计算。

这一扩展很有意义，但好像已经超越了地图空间信息，因为地图图形表达以地图要素为基本单元。在他们的处理中，一个地图要素由有限个像元表达，这好像已经是地图的图像信息量，而不是地图的图形的信息量。例如图11(b)的3个厕所符号具有相同的地图图形信息，而具有非常不同的地图图像信息。

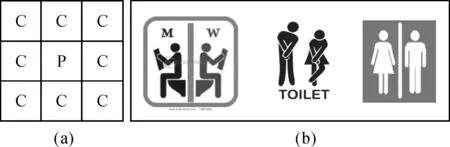
图11　地图的图形信息与图像信息：同类符号含不一样的图像信息(图片来源于网络)Fig.11　The graphic and image information of map: same types of symbols with different image information

2.3广义地图信息论的发展现状

广义地图信息论既具有信息论的坚实基础理论，又体现了地图信息度量的独特性，国内外学者在该框架下对地图解译、地图综合、地图设计等方面开展了大量的研究工作，真正促进了地图信息度量理论向实践的快速发展。下面将对国内外学者在广义地图信息度量框架下开展的研究工作进行回顾和总结。

2.3.1基于广义地图信息的地图解译

近年来，广义地图信息论已经在地图可读性度量方面被广泛应用，地图可读性关系到地图使用者能否有效地获得地图上提供的信息，在移动终端与互联网在线地图广泛应用的今天，对地图可读性的度量尤为重要。文献[27—29]在地图几何信息量基础上，又细分了符号数量与符号本身的大小与形态信息，采用人工判读结果对地图信息度量结果进行评价，结果发现在测试数据上(比例尺为1∶1万、1∶5万的地形图)符号的数量与几何信息量最能表征地图的可读性，而符号本身的复杂性(如大小与形态等)对地图可读性的影响不明显[27-29]。

文献[30]计算1∶5万与1∶25万不同地貌的高线地图的几何与拓扑信息量，认为地图信息量计算结果与人的观察结果是吻合的。文献[31]采用广义地图信息度量方法对我国西部1∶5万测图工程的地形图产品的质量进行评价，认为地图信息度量方法是我国现有产品规范的有力补充。

2.3.2基于广义地图信息的地图综合

地图综合是多比例尺地图生产与跨比例尺地图更新的关键技术，地图综合中地图信息量随比例尺(或尺度)的变化规律(图12)是评价综合质量与地图服务质量的基础问题。

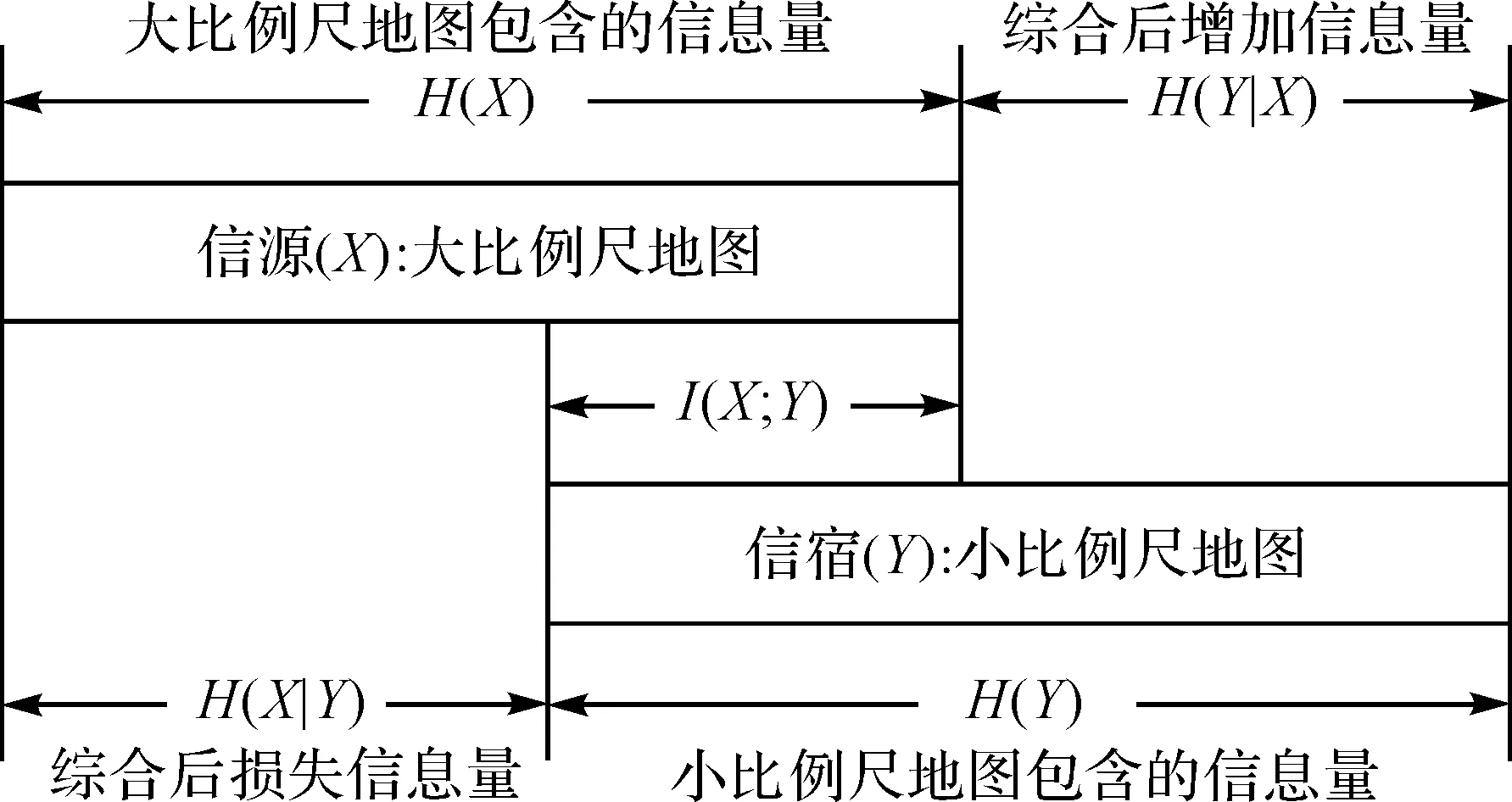
图12　地图综合过程中的信息传递模型(改自文献[7])Fig.12　The information transmission model in map generalization[7]

文献[32]对不同比例尺下的地图信息变化作了系统试验，发现跟比例尺的平方根比与相应的几何信息比很一致。

文献[20]认为几何信息量基于V图的计算方法一方面反映了地图实体对空间的划分，另一方面亦体现出了地物间的邻接关系，是语法层次地图信息量的主要体现，采用几何信息量指导点群的自动综合，与手工综合结果极为接近。

文献[33]对几何信息量进行了进一步扩展，研究了目标层次上地图信息的传递规律[7]，并借助地图几何信息度量方法对现有的线要素化简算法进行评价，认为地图信息量指标优于当前综合算法评价指标。

文献[21]采用基于V图的几何信息量计算方法以制图综合中移位和合并两种典型操作为例，研究了面目标尺度变换中的信息量衰减规律，可为综合算法评价提供客观依据。

2.3.3基于广义地图信息的地图设计

广义地图信息量度量亦被推广应用于地图设计，如地图注记配置、地图色彩数目确定。文献[34]引入几何信息量用于面状要素的注记配置，从地图信息的角度阐明地图注记配置的本质是降维，配置优化的目标是最大限度保持原有的几何信息量。为此，他们创建了基于熵线的注记配置(图13)，这一方法不仅使得注记配置的效果得到了改进, 更是注记配置思维由关注具体图形到关注一般本质的一种提升。

图13　基于熵线的注记配置[34]Fig.13　Name placement based on entropy[34]

文献[14]从地图信息量负载的角度研究地图色彩数目的确定问题(图14表示了色彩数目与地图有益信息的关系)，从理论上证明了经验性的色彩数目确定原则(不超过7～8种)。

2.3.4其他广义地图信息的定义

广义地图信息度量亦延伸到影像的信息度量，各种影像(如遥感影像)加符号后成为一种特殊的地图-影像地图。引入广义地图信息论对遥感影像的信息量进行度量亦受到了国内外学者的关注，对遥感影像进行度量一方面可以对遥感影像的质量进行评价，另一方面也可以对影像处理方法的性能进行衡量[35-36]。现有的遥感影像信息度量方法实际上与文献[18]提出的广义地图信息理论有着共通之处，例如采用一阶邻近像元灰度差异[25]或相关性[37]度量影像信息实际上与地图专题信息量的计算方法极为相似：一阶邻近像元实际上等同于一阶Voronio邻近，而像元灰度差亦与地图符号的类别差类似。然而，对遥感影像每个像元的信息量进行度量时，依然采用的是灰度值出现的概率进行计算[38]，实际上这种信息量仅是统计信息量：与像元的空间分布无关，且仅存在一个灰度值时，有像元但无信息量。

图14　色彩数目与有益信息的关系[25]Fig.14　The relationship between number of colours and entropy[25]

3广义地图信息论研究的未来方向

地图信息度量经过近半个世纪的发展，已经从狭义地图信息论发展为广义地图信息论，而且广义地图信息论在现代地图学乃至遥感领域均取得了实质性的应用成果。广义地图信息论的研究方兴未艾，本文认为未来广义地图信息论的发展在于扩展与整合。

3.1广义地图信息论的3大扩展方向

本文认为未来广义地图信息论会从3大方向扩展(图15)：①由语法地图信息向语义和语用;②由客观概率向主观、逻辑概率;③由空间到时空。

3.1.1由语法地图信息向语义和语用地图信息延伸

从语言层次上来看，目前广义地图信息论主要度量的是语法层次上的地图信息，但是语法地图信息度量是语用和语义地图信息度量的重要基础[14]。近年来，已经有学者尝试将广义地图信息论拓展到语义层次上，例如，采用加权V图拓展的几何信息量计算[19]; 考虑水平和垂直方向变化对数字高程模型的几何信息量进行度量[39]。如何从人类认知的角度将语法地图信息度量推广到语义和语用地图信息度量将是未来发展的重要方向，甚至可能需要对信息论的基础理论进行修正。

图15　广义地图信息论的3大扩展方向Fig.15　Three research directions of general cartographic information theory

3.1.2由客观概率向主观、逻辑概率的转变

从概率种类来看，当前在广义地图信息论框架下表征地图符号不确定性的依然是客观概率，即根据事件发展的客观性统计出来的概率。客观概率只能用于完全可重复事件，对于很多现实事件并不适用。地图服务人类认知的特点，决定了地图信息度量中符号概率必须融入人的主观性，即主观概率。更深层次上，可能需要对命题或预言被不同的人判定为真的概率(即逻辑概率)进行考虑。在概率计算中纳入人的认知约束也可能是将语法信息向语义和语用信息延伸的一种途径，一些统计学理论(如贝叶斯理论)或许可以提供理论方法支撑。

3.1.3由空间信息到时空信息的发展

当前广义地图信息论考虑的时空专题已经从狭义地图信息论的统计信息扩展到几何、专题、拓扑等方面。进一步，伴随着大数据时代的到来，传统地图已经向可视化解析(visualanalytics)迈进，表现为语义关系一致的四维时空位置信息的集合，其特点包括：高动态、个性化、高精度、精细化、真三维、同移动互联网及物联网紧密结合[40-41]。可视化解析中包含的多维时空动态信息，时间和空间信息的交互作用、传递及耦合对广义地图信息论提出了新的挑战。

3.2图形与图像统一的信息论

影像是现实世界的写照，是比较具体的表达，而地图是符号化、抽象化的表达。介于两者之间是影像地图，一种在正射影像上加地图符号的新型地图。影像地图已经得到广泛的应用。图16为谷歌地图提供的影像地图截屏。要研究影像地图的信息量以及影像到地图的信息传输理论，必须研究图形与图像统一的信息度量，或者建立二者的转换关系。

图16　从影像到地图：符号化(谷歌地图截屏)Fig.16　From image to map: symbolization (screenshots from Google map)

影像的信息度量本质上与地图信息度量存在共通性，当前影像信息度量实际上还多是对统计信息的度量，而对影像反映的空间信息本质属性顾及不足。借鉴广义地图信息论中几何信息量和专题信息量的度量策略发展影像的空间信息度量模型将是未来图形与图像统一信息论研究的重要方向。

4总结与展望

本文对近半个世纪以来，信息论在地图学领域的发展进行了回顾，将地图信息度量区分为两个发展阶段：狭义地图信息论与广义地图信息论。进而，对这两个发展阶段的研究成果、特点进行了系统的归纳与评述。本世纪初提出广义地图信息度量理论后，地图信息度量对现代地图学发展产生了重要的推动作用，在地图质量/可读性评价、地图综合、地图设计等诸多领域产生了新的变革，并取得了一系列标志性的应用成果。

本文同时对广义地图信息论的发展现状进行了定位，在此基础上从语言层次、概率种类与时空专题3个方面对广义地图信息论的发展方向进行了展望，同时亦对影像与地图信息论的统一问题进行了初步的探讨。通过对地图信息度量领域的发展进行梳理，希望能够起到抛砖引玉的作用，促进广义地图信息论的新发展。

参考文献：

[1]WOOD D, FELS J. The Power of Maps[M]. New York: Guilford Press, 1992.

[2]WOOD D, FELS J, PICKLES J. The Natures of Maps: Cartographic Constructions of the Natural World[M]. Chicago: University of Chicago Press, 2009.

[3]ROBINSON A H. The Look of Maps[M]. Madison: University of Wisconsin Press, 1952.

[4]KEATES J S. The Perception of Colour in Cartography[C]∥Proceedings of the Cartographic Symposium. Edinburgh: [s.n.], 1962: 19-28.

[5]SHANNON C E. A Mathematical Theory of Communication[J]. The Bell System Technical Journal, 1948, 27(3): 379-423.

[6]SUKHOV V I. Information Capacity of a Map Entropy[J]. Geodesy and Aerophotography, 1967, 10(4): 212-215.

[7]邓敏, 徐震, 赵彬彬, 等. 地图概括中空间目标几何信息传递模型研究[J]. 地球信息科学学报, 2010, 12(5): 655-661. DENG Min, XU Zhen, ZHAO Binbin, et al. A Transmission Model of Geometrical Information for Individual Spatial Objects in Cartographic Generalization[J]. Journal of Geo-Information Science, 2010, 12(5): 655-661.

[8]COVER T M, THOMAS J A. Elements of Information Theory[M]. 2nd ed. New Jersey: John Wiley & Sons, 2006.

[10]祝国瑞, 黄采芝. 一览图上居民地要素语义信息量的测度[J]. 武汉测绘学院学报, 1985, 10(4): 89-96.

ZHU Guorui, HUANG Caizhi. On the Measurement of Map Information of Settlements[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1985, 10(4): 89-96.

[11]何宗宜. 地图信息含量的量测研究[J]. 武汉测绘科技大学学报, 1987, 12(1): 70-80. HE Zongyi. A Study of the Method for Measuring the Information Content of Map[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1987, 12(1): 70-80.

[12]NEUMANN J. The Topological Information Content of a Map An Attempt at a Rehabilitation of Information Theory in Cartography[J]. Cartographica, 1994, 31(1): 26-34.

[13]KNOPFLI R. Communication Theory and Generalization[M]∥TAYLOR D R F. Graphic Communication and Design in Contemporary Cartography. New York, Chichester: John Wiley & Sons, 1983: 177-218.

[14]BJ∅RKE J T. Exploration of Information Theoretic Arguments for the Limited Amount of Information in a Map[J]. Cartography and Geographic Information Science, 2012, 39(2): 88-97.

[15]BJ∅RKE J T. Framework for Entropy-Based Map Evaluation[J]. Cartography and Geographic Information Systems, 1996, 23(2): 78-95.

[16]刘宏林. 地图信息的科学含义再探[J]. 测绘学院学报, 1992(2): 51-55.

LIU Honglin. Exploring the Scientific Implication of Map Information Again[J]. Journal of the Institute of Surveying and Mapping, 1992(2): 51-55.

[17]SHANNON C E, WEAVER W. The Mathematical Theory of Communication[M]. Urbana: University of Illinois Press, 1964.

[18]LI Zhilin, HUANG Peizhi. Quantitative Measures for Spatial Information of Maps[J]. International Journal of Geographical Information Science, 2002, 16(7): 699-709.

[19]王少一, 王昭, 杜清运. 顾及地图要素级别的几何信息量量测方法[J]. 测绘科学, 2007, 32(4): 60-62. WANG Shaoyi, WANG Zhao, DU Qingyun. A Measurement Method of Geometrical Information Considering Multi-Level Map Feature[J]. Science of Surveying and Mapping, 2007, 32(4): 60-62

[20]王昭, 费立凡. 基于语法层的地图综合信息量原则[J]. 测绘科学, 2007, 32(6): 21-23.

WANG Zhao, FEI Lifan. Syntax-Based Information Quantity Rule for Automatic Map Generalization[J]. Science of Surveying and Mapping, 2007, 32(6): 21-23.

[21]艾廷华, 何亚坤, 杜欣. GIS数据尺度变换中的信息熵变化[J]. 地理与地理信息科学, 2015, 31(2): 7-11.

AI Tinghua, HE Yakun, DU Xin. Information Entropy Change in GIS Data Scale Transformation[J]. Geography and Geo-Information Science, 2015, 31(2): 7-11.

[22]张辉. 地图信息度量的方法及其应用[J]. 测绘与空间地理信息, 2010, 33(3): 236-239. ZHANG Hui. The Approach and Application of Map Information Measurement[J]. Geomatics & Spatial Information Technology, 2010, 33(3): 236-239.

[23]刘慧敏, 樊子德, 邓敏, 等. 地图上等高线信息度量的层次方法研究[J]. 测绘学报, 2012, 41(5): 777-783. LIU Huimin, FAN Zide, DENG Min, et al. A Hierarchical Approach to Measuring the Information Content of the Contours in a Map[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 777-783.

[24]陈杰, 邓敏, 徐枫, 等. 面状地图空间信息度量方法研究[J]. 测绘科学, 2010, 35(1): 74-76, 49.

CHEN Jie, DENG Min, XU Feng, et al. A Measurement Approach for Spatial Information of Area Map[J]. Science of Surveying and Mapping, 2010, 35(1): 74-76, 49.

[25]刘慧敏. 地图空间信息量的度量方法研究[D]. 长沙: 中南大学, 2012. LIU Huimin. Methods of Measuring the Spatial Information Content of a Map[D]. Changsha: Central South University, 2012.

[26]WU Huayi, ZHU Haijun, LIU Yi. A Raster-based Map Information Measurement for QoS[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2004, 35(B2): 365-370.

[27]HARRIE L, STIGMAR H. An Evaluation of Measures for Quantifying Map Information[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(3): 266-274.

[28]STIGMAR H, HARRIE L. Evaluation of Analytical Measures of Map Legibility[J]. The Cartographic Journal, 2011, 48(1): 41-53.

[29]HARRIE L, STIGMAR H, DJORDJEVIC M. Analytical Estimation of Map Readability[J]. ISPRS International Journal of Geo-Information, 2015, 4(2): 418-446.

[30]刘文锴, 乔朝飞, 陈云浩, 等. 等高线图信息定量度量研究[J]. 武汉大学学报(信息科学版), 2008, 33(2): 157-159.

LIU Wenkai, QIAO Chaofei, CHEN Yunhao, et al. Quantitative Measures for Spatial Information of Contour Maps[J]. Geomatics and Information Science of Wuhan University, 2008, 33(2): 157-159.

[31]王红. 基础地理信息地形数据库信息量度量方法研究[D]. 阜新: 辽宁工程技术大学, 2010.

WANG Hong. Research on Quantity Measurement of Basic Geographic Information in Topographic Database[D]. Fuxin: Liaoning Technical University, 2010.

[32]LI Zhilin, HUANG Peizhi. Transformations of Spatial Information in Multi-scale Representation[C]∥Proceedings of the 20th International Cartographic Conference. Beijing: Scientific and Technical Program Committee, 2001.

[33]邓敏, 樊子德, 刘慧敏. 层次信息量的线要素化简算法评价研究[J]. 测绘学报, 2013, 42(5): 767-773. DENG Min, FAN Zide, LIU Huimin. Performance Evaluation of Line Simplification Algorithms Based on Hierarchical Information Content[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 767-773.

[34]王昭, 吴中恒, 费立凡, 等. 基于几何信息熵的面状要素注记配置[J]. 测绘学报, 2009, 38(2): 183-188. WANG Zhao, WU Zhongheng, FEI Lifan, et al. Automatic Name Placement of Area Feature: A Metric Information Approach[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(2): 183-188.

[35]张恒, 冯德俊, 朱军, 等. 遥感影像信息量与空间分辨率的关系研究[J]. 应用光学, 2014, 35(3): 409-413. ZHANG Heng, FENG Dejun, ZHU Jun, et al. Relationship between Information Content and Spatial Resolution of Remote Sensing Images[J]. Journal of Applied Optics, 2014, 35(3): 409-413.

[36]韩鹏, 龚健雅, 李志林, 等. 遥感影像分类中的空间尺度选择方法研究[J]. 遥感学报, 2010, 14(3): 507-518.

HAN Peng, GONG Jianya, LI Zhilin, et al. Selection of Optimal Scale in Remotely Sensed Image Classification[J]. Journal of Remote Sensing, 2010, 14(3): 507-518.

[37]林宗坚, 张永红. 遥感与地理信息系统数据的信息量及不确定性[J]. 武汉大学学报(信息科学版), 2006, 31(7): 569-572. LIN Zongjian, ZHANG Yonghong. Measurement of Information and Uncertainty of Remote Sensing and GIS Data[J]. Geomatics and Information Science of Wuhan University, 2006, 31(7): 569-572.

[38]张盈, 张景雄. 顾及空间相关性的遥感影像信息量的度量方法[J]. 测绘学报, 2015, 44(10): 1117-1124. DOI: 10.11947/j.AGCS.2015.0140417.ZHANG Ying, ZHANG Jingxiong. Measure of Information Content of Remotely Sensed Images Accounting for Spatial Correlation[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1117-1124. DOI: 10.11947/j.AGCS.2015.0140417.

[39]HU Lujin, HE Zongyi, LIU Jiping, et al. Method for Measuring the Information Content of Terrain from Digital Elevation Models[J]. Entropy, 2015, 17(10): 7021-7051.

[40]王家耀. 关于信息时代地图学的再思考[J]. 测绘科学技术学报, 2013, 30(4): 329-333.

WANG Jiayao. Rethinking about the Information Age Cartography[J]. Journal of Geomatics Science and Technology, 2013, 30(4): 329-333.

[41]周成虎, 朱欣焰, 王蒙, 等. 全息位置地图研究[J]. 地理科学进展, 2011, 30(11): 1331-1335.

ZHOU Chenghu, ZHU Xinyan, WANG Meng, et al. Panoramic Location-based Map[J]. Progress in Geography, 2011, 30(11): 1331-1335.

(责任编辑：张燕燕)

修回日期： 2016-05-24

First author： LI Zhilin(1960—)，male，PhD,professor,majors in cartography,GIS and remote sensing.

中图分类号：P208

文献标识码：A

文章编号：1001-1595(2016)07-0757-11

基金项目：国家973计划(2012CB719901)，国家自然科学基金(41471383)；香港研究资助局基金(B-Q49E)

收稿日期：2016-05-03

第一作者简介：李志林(1960—)，男，博士，教授，主要研究方向为地图制图、地理信息科学及遥感等。

Entropy-based Cartographic Communication Models：Evolution from Special to General Cartographic Information Theory

LI Zhilin1,2，LIU Qiliang2,3，GAO Peichao2

1. Joint State-Province Engineering Laboratory of Spatial Information Technology for High-speed Railway Safety，Southwest Jiaotong University, Chengdu 611756, China； 2. Department of Land Surveying and Geo-Informatics, The Hong Kong Polytechnic University, Hong Kong, China； 3. Department of Geo-Informatics, Central South University, Changsha 410083, China

Abstract：Map is a kind of powerful means to help people in understanding the objective world. The key function of map is to transmit spatial information. The measurement of spatial information of maps dates back to 1960s, when the information theory of communication was introduced to the field of cartography. The introduction led to a new branch of cartography, i.e. cartographic information theory. This paper provides a review of the development of cartographic information theory over the past 50 years. Emphasis is on the evolution from the special to the general cartographic information theory.

Key words：cartography; information theory; cartographic information theory; special cartographic information theory; general cartographic information theory

引文格式：李志林、刘启亮，高培超.地图信息论：从狭义到广义的发展回顾[J].测绘学报，2016,45(7)：757-767. DOI:10.11947/j.AGCS.2016.20160235.

LI Zhilin，LIU Qiliang，GAO Peichao.Entropy-based Cartographic Communication Models：Evolution from Special to General Cartographic Information Theory[J]. Acta Geodaetica et Cartographica Sinica,2016,45(7):757-767. DOI:10.11947/j.AGCS.2016.20160235.