土壤水入渗补给数值模拟——以河北栾城为例

吴庆华，王贵玲，张家发，朱国胜，张　薇

(1.长江科学院 水利部岩土力学与工程重点实验室，武汉　430010; 2.中国地质大学 教育部长江三峡库区地质灾害研究中心，武汉　430074; 3.中国地质科学院 水文地质环境地质研究所，石家庄　050061)



土壤水入渗补给数值模拟——以河北栾城为例

吴庆华1,2,3，王贵玲3，张家发1，朱国胜1，张薇3

(1.长江科学院 水利部岩土力学与工程重点实验室，武汉430010; 2.中国地质大学 教育部长江三峡库区地质灾害研究中心，武汉430074; 3.中国地质科学院 水文地质环境地质研究所，石家庄050061)

摘要：由于通过短时间尺度的土壤水动态监测数据难以准确获得土壤水入渗补给的规律，因此在中国地质科学院栾城试验场开展了长时间尺度(5 a)的土壤水动态监测试验，监测深度为340 cm。利用Hydrus-1D软件的双渗透(基质流区和大孔隙流区)模型进行数值模拟，并采用最小函数法对模型进行参数反演。为克服地表复杂的气象条件可能给模拟结果带来较大误差，选取140 cm深度为模型上边界。研究结果表明，基质流区(m)和大孔隙流区(F)土壤水动力特征参数nm，nF，αm和αF，大孔隙流区饱和导水系数KsF对模型入渗补给量的灵敏性最高，并被选取为模型反演参数。 总体上，土壤体积含水量的模拟值能较好地拟合其实测值，其决定系数为0.78。地下水入渗补给速率具有年际变化特征，但在年内具有明显的季节性，即在雨季达到最大，然后缓慢减小。年均入渗补给速率为220 mm/a，其中由优先流引起的入渗补给量为211 mm/a，这表明地下水入渗补给以优先流为主。该研究成果可提高对地下水入渗补给规律的认识，同时可为地下水资源评价与农业节水管理等提供参考。

关键词：土壤水；地下水；入渗补给；数值模拟；Hydrus-1D

1研究背景

地下水入渗补给是指降雨或灌溉水通过土壤垂向入渗补给地下含水层的现象。地下水入渗补给是农业水利、水文地质与地下水污染防治等领域研究的重点，因此，一直受到该领域学者的高度重视。研究地下水入渗补给的方法主要有示踪法[1-2]、地中渗透仪法[3-4]、水均衡法[5]、地下水位波动法[6-7]、零通量面法[8]和数值模拟法[9-11]等，但每种方法都有其应用的适用性。与其它方法相比，数值模拟方法具有对地下水入渗补给过程准确刻画与预测等优点，因此被广泛应用。目前国际上用于研究土壤水入渗的数值模型主要有：连续性模型、两区或多区模型和网络状模型[12]。连续性模型假设土壤孔隙是连续的、均匀的，并利用Richards方程描述其非饱和土壤水流。根据孔隙的导水能力，将该模型分为单孔隙、双孔隙和多孔隙均匀流介质模型。其中单孔隙水流均匀且土壤水在运移过程中处于平衡状态，适用于均质介质，但Ross和Smettem[13]认为在Richards方程中土壤含水量与水势之间的平衡是时间的函数，并非真的平衡流。双孔隙和多孔隙连续模型假设土壤水流各自通过自己的孔隙通道，无相互作用，且水流为稳定流，适用于结构性土壤。两区模型和两流区的共同点是将整个土壤分为2个区，不同点在于两区模型将土壤流区划分为可流动区和不可流动区，而两流区模型则划分为快速流动区(优先流)和慢流动区(基质流)[14-18]。两流区模型更加真实反映实际土壤水流情况，但主要存在2方面难题：一是两区模型所需参数多，大多数参数在室内外均难以测得，主要通过参数反演程序获取，这对模型运行的稳定性与参数验证的唯一性提出了挑战。而且目前用于模型田间土壤水运移的监测数据的时间序列短，难以客观反演参数在时间上的代表性，因此在实际工作中需要观测长序列数据进行模型参数反演。二是将模型应用田间时将会遇到上边界条件(大气地表)难以控制，土壤蒸发与植物的蒸腾量难以准确获取等问题。如X.Lu 等[19]利用Hydrus-1D软件对2004年河北栾城地区地下水入渗补给进行模拟，分别采用Feddes(1978年)模型和Penman-Monteith公式对植物根系吸水项和作物蒸发蒸腾量进行估算，存在经验参数众多，计算精度低，难以准确刻画土壤表层边界条件等问题。如将模型上边界选择在地表一定深度以下且植物根系吸水作用不存在或可忽略的区域，则可回避地表复杂的气象条件。

综上所述，地表条件复杂且各项边界条件难以精确测量与确定，以及用于模型参数反演数据的观测时间短等不足，对数值模拟均造成一定的影响。为此，本文选择中科院栾城试验场近5 a的土壤水动态监测数据对该地区地下水入渗补给进行了数值模拟研究，其研究成果对于探索长时间尺度地下水入渗补给规律以及建立准确的数值模型具有重要意义，也可对该地区的地下水资源评价以及农业节水等方面提供科学参考。

2研究区概况

本试验选取中国科学院栾城试验场，研究地下340 cm深度范围内土壤水动态变化规律。栾城试验场位于河北平原栾城县，介于37°47′～38°01′N，114°28～114°47′E，占地面积0.4 km2，属太行山东麓倾斜平原南部，代表河北平原深厚包气区，地下水埋深37.0 m，地层岩性复杂，夹杂薄层黏土或粉质黏土。年均气温12.8 ℃，年均降雨量为450 mm(1990—2010年)，集中于6—9月份。年均蒸发量为1 470 mm(1990—2010年)[20]。主要作物为棉花、冬小麦和夏玉米，以地下水进行漫灌。

3试验材料与方法

3.1试验设计

在中国科学院栾城试验场开展土壤水动态监测试验，用于研究种植条件下长序列土壤水运移动态变化，定量分析优先流在土壤水入渗补给地下水中的作用。采用中国地质科学院水文地质环境地质研究所研制的WM-1型水银式负压计和英国的IH-II型中子水分仪分别监测土壤剖面中的土壤水势和含水量，监测深度为3.4 m，分别布设20个负压计和20个中子仪监测点。WM-1系统测量与计算负压原理和中子仪标定方程详见文献[21]。负压计和中子仪监测剖面相距1.0 m，且两者的监测点位置相互对应，即在0～1 m，1～2.6 m，2.6～3.4 m深度范围内，分别每隔10，20，40 cm深度安装1个负压计和1个中子监测点。负压计和中子测量的监测频率为：常规3 d观测1次。当有大降雨或灌溉时，加密监测频率，即降雨或灌溉事件期间0.5 h 1次；结束后6 h内0.5 h 1次；6～12 h内1 h 1次；12～48 h内3 h 1次；大于48 h，6～12 h 1次，逐渐加长时间间隔。每次测量时间为5 min。试验期间灌溉量、降雨量与蒸腾量均由中科院栾城试验站提供监测。

监测时间为2003年3月到2013年1月。通过对监测数据的分析，优选2003—2007年之间的系列数据进行土壤水动态分析与优先流现象发育特征研究。

3.2数值模拟

3.2.1数学模型

采用基于Richards方程的双渗透模型描述土壤水流方程，其控制方程如式(1)至式(5)[22]：

(1)

(2)

(3)

(4)

(5)

式中：θF，θm，θ分别为大孔隙、基质流区以及整个流区的体积含水量(cm3/cm3)；SF和Sm分别为大孔隙和基质流区植物吸收项(d-1)；hF和hm分别为大孔隙流和基质流区土壤基质势(cm)；KF和Km分别为大孔隙和基质流区导水系数(cm/d)；Γw为大孔隙与基质流区交换水量(d-1)；ω为大孔隙流区占整个流区比重；αw为一阶土壤水传输系数(cm-1·d-1)；β为土粒几何形状因子，如当土粒形状为长方体和球形时，其取值分别为3.0和15.0，在本文中取值15.0；γ为经验系数，一般取值为0.4；a为基质区中心与大孔隙边界之间的距离(cm)；Ka为基质与大孔隙区界面之间的渗透系数(cm/d)；t为时间(d)；z为垂向坐标轴，向上为正(cm)。

对于垂向一维模型的边界条件仅需考虑上边界与下边界条件。上边界选在地下深-140 cm界面处，其主要原因：其一，该界面以下仅有少量冬小麦根系发育，其植物根系吸水作用可忽略不计，即SF和Sm均为0；其二，地表条件复杂，难以准确监测植物的蒸发蒸腾，且在长时间尺度的土壤水动态试验中难以适用；其三，该试验的目的是研究入渗补给过程中的优先流， 200 cm以下地下水常年入渗补给地下水[5]，则将上边界选在140 cm处回避了地表条件复杂的缺点。但在没有明显植物根系吸水作用的前提下尽量选择较浅深度作为上边界，因为土壤越浅，其土壤水动态变化相对较大，越有利于模型运行。

上边界定义为变压力水头边界，利用试验期间140 cm深度处土壤水势数据，用式(6)表示：

(6)

下边界为零梯度自由排水边界，该边界条件适用于地下水水位埋深较大的田间试验。该边界为变流量边界，用式(7)表示：

(7)

初始条件为土壤基质势能，用式(8)表示：

(8) 表1　栾城试验站田间土壤水动态试验参数反演结果Table 1　Results of parametric inversion for the field test at Luancheng site

3.2.2数值模型

采用Hydrus-1D 4.0软件进行土壤水优先流模拟。模拟深度140～340 cm，共离散为200个单元，离散精度为1 cm。共有9个土壤含水量和水势监测点，其位置分别为Z=140， 160， 180， 200， 220， 240， 260，300，340 cm。模拟时间从2003年4月9日至2007年10月24日，共计1 618 d。时间单位为d，初始时间步长为0.000 1 d，最小步长为0.000 01 d，最大为5 d。最大迭代次数为20，在参数反演迭代过程中，如达到迭代收敛时所需要的迭代次数小于3时，时间步长乘以常数1.3增加步长，减少运行时间；如迭代次数大于7次时，时间步长将乘以0.7减小步长，提高迭代运行精度。迭代中可容许的最小土壤体积含水量为0.000 1，水势变化为1 cm。

3.2.3参数反演

参数反演是一种间接根据土壤水盐运移数据获取土壤水力或溶质运移参数的方法。该方法的实质是利用一种最小函数法使观测数据与模拟值相差最小的方法。Hydrus-1D采用nek等提出的最小函数法进行参数反演，利用Levenberg-Marquardt 非线性的牛顿与最快骤降法使主函数最小[23]。双渗透模型中共涉及17个参数，13个独立参数，给模型的参数反演带来很大的不确定性[15]。为了尽量减少反演过程中参数个数，则需要对13个独立的参数进行灵敏性分析，仅对灵敏性较高的参数进行参数反演，提高模型的确定性与准确度。采用式(9)进行参数灵敏性评估[24]：

(9)

式中：Skl为灵敏系数；bl为评估的参数；qk为参数灵敏性评价对象，即当参数改变1%时模型输出结果qk的变化值；b为参数b的矢量；el为l阶矢量单位。选取下边界出流速率作为参数灵敏性评价对象(qk)。

4结果与讨论

4.1参数反演

总体上大孔隙流区中参数的灵敏度要高于基质流区。在所有参数中，大孔隙区的土壤特征参数nF和αF的灵敏性最高，其次为基质流区中的土壤特征参数nm和土壤残余含水量(θrm)以及大孔隙区中饱和渗透系数(KsF)。2区中的土壤饱和含水量(θsm和θsF)和孔隙弯曲度(lm和lF)最不灵敏。

θrm根据土壤颗粒组成采用RETC软件估算值0.09。则在参数反演中，共选取nm，αm，nF，αF，KsF、ω和Ka进行参数反演。虽然ω和Ka的参数灵敏性不高，但其无法从实验中获得，则需要通过反演获取。θsm和Ksm采用扰动土土柱饱和含水率和饱和导水系数，分别取值为0.360和0.5 cm/d。根据经验，θrF，θsF，lm，lF，β，γ和a分别取值为0.00，0.600，0.5，0.5，15.0，0.4和0.1。参数反演程序中各参数的初始值及其范围和反演结果见表1。

图1　体积含水量观测值与模拟结果对比

4.2地下水入渗补给模拟

图1为土壤体积含水量实测与模拟值随时间变化对比图。从图1可知，体积含水量模拟值能较好地拟合观测值，其决定系数为0.78，表明模拟结果可靠。图2为总入渗补给量与降雨-灌溉-蒸发随时间变化关系。

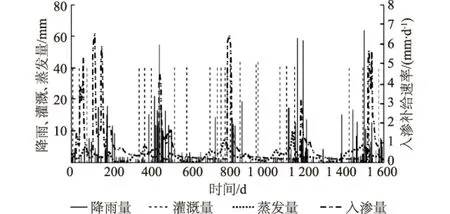
图2　总入渗补给量与降雨-灌溉-蒸发 随时间变化关系

图3　累积入渗补给量随时间变化曲线

入渗补给速率具有年际变化规律，总体上在雨季达到最大，然后缓慢减小。但其最大值比雨季晚1个月才会到达，表明在雨季时期地表降雨需要大概1个月时间才能到达340 cm深度处，而在干旱时期则需要更长时间。另外，入渗补给速率并不随灌溉量而发生显著变化，尽管其灌溉量大，灌溉强度高，这主要是因为灌溉时土壤干旱缺水，大部分水分均被浅层土壤吸收以及用于作物蒸发蒸腾。虽然根据灌溉时期土壤剖面含水量与水势可以确定灌溉水在很短的时间内将运移至200 cm以下，甚至更深，但由于土壤干旱，其优先流入渗的灌溉水一部分用于补充其周围土壤基质水分亏缺，另一部分则以相对较慢优先流速度入渗深层土壤，导致在340 cm深度处并无明显反应。但从整个入渗补给过程来看，灌溉时期渗入200 cm以下水分均属于由大孔隙优先流所贡献，不论其最终是以补缺土壤水分或者以缓慢优先流形式穿透340 cm界面。入渗补给速率最大值一般发生在雨季中降雨量最大时刻，土壤剖面前期相对湿润，加速水分传输，有利于优先流激发。

图3为累积地下水入渗补给量的评价结果。从2003-04-04至2007-09-27共计1 618 d，总入渗补给量为975 mm，年均220 mm/a。其中2004年度为195 mm/a，与该研究区Br-和T示踪的研究结果(215 mm/a)具有较好的一致性[1]。由优先流引起的入渗补给量为939 mm，占总入渗补给量96.3%，表明研究区0～340 cm深度范围内地下水入渗补给主要是以优先流方式补给地下水。但目前的研究仅局限于340 cm深度范围，对于340 cm至潜水位(埋深3 700 cm)土壤水运动模式有待于进一步探讨。根据钻孔岩性资料调查， 340～500 cm主要为黏土， 500 cm以下主要为粉细砂。随深度增加，土壤大孔隙呈指数减少，大孔隙优先流程度明显降低。但土壤结构如黏土块体裂隙和因生物沉积作用形成的土壤孔隙等均是良好的优先流通道。另外由于粉砂土存在斥水性，导致500 cm以下的粉砂岩土层为指流发育的主要场所。总之，该研究区降雨-灌溉水主要以优先流方式入渗补给浅层地下水。

5结论

(1) 选取140 cm深度处为模型上边界，回避了地表复杂的气象条件，可提高模拟结果的准确性。

(2) 利用最小函数法对双渗透模型进行参数进行反演，基质流区(m)和大孔隙流区(F)土壤水动力特征参数nm，nF，αm和αF，大孔隙流区饱和导水系数KsF以及两流区水分交换系数Ka对地下水入渗补给量的灵敏性最高。

(3) 利用Hydrus-1D双渗透模型能准确模拟长时间尺度的土壤水动态变化。总体上，地下水入渗补给速率具有年际变化规律。年内雨季最大，然后缓慢减小。

(4) 年均地下水入渗补给速率为220 mm/a，其中由优先流引起的入渗补给量为211 mm/a，说明地下水入渗以优先流为主。

参考文献：

[1]WANG B,JIN M,WANG W,etal.Estimating Groundwater Recharge in Hebei Plain,China under Varying Land Use Practices Using Tritium and Bromide Tracers[J]. Journal of Hydrology, 2008, 356: 209-222.

[2]KÖHNE S, LENNARTZ B, KÖHNE J M,etal. Bromide Transport at a Tile-drained Field Site: Experiment, and One- and Two-dimensional Equilibrium and Non-equilibrium Numerical Modeling[J]. Journal of Hydrology, 2006, 321(1/4): 390-408.

[3]王丙国. 地下水补给评价方法研究[D]. 武汉：中国地质大学,2008.

[4]KITCHING R,SHEARER T R,SHEDLOCK S L.Recharge to Bunter Sandstone Determined from Lysimeters[J]. Journal of Hydrology, 1977, 33(3/4): 217-232.

[5]吴庆华, 王贵玲, 蔺文静,等. 太行山山前平原地下水补给规律分析:以河北栾城为例[J]. 地质科技情报, 2012, 31(2): 99-105.

[6]HEALY R, COOK P. Using Groundwater Levels to Estimate Recharge[J]. Hydrogeology Journal, 2002, 10(1): 91-109.

[7]SINGH R M,SINGH K K,SINGH S R.Water Table Fluctuation between Drains in the Presence of Exponential Recharge and Depth-dependent Evapo-transpiration[J]. Journal of Irrigation and Drainage Engineering, 2007, 133(2): 183-187.

[8]荆恩春, 费瑾, 张孝和. 土壤水分通量法实验研究[M]. 北京: 地震出版社, 1994.

[9]JIN F F. An Equatorial Ocean Recharge Paradigm for ENSO. Part I: Conceptual Model[J]. Journal of the Atmospheric Sciences, 1997, 54(7): 811-829.

[10]COES A, SPRUILL T B, THOMASSON M J. Multiple-method Estimation of Recharge Rates at Diverse Locations in the North Carolina Coastal Plain, USA[J]. Hydrogeology Journal, 2007, 15(4): 773-788.

[11]ARSHAD M, AHMED N, CHEEMA J M. Modeling Approach for the Assessment of Recharge Contribution to Groundwater from Surface Irrigation Conveyance System[J]. Irrigation and Drainage Systems, 2008, 22(1): 67-77.

[12]KÖHNE J M, KÖHNE S, SIMNEK J. A Review of Model Applications for Structured Soils: A) Water Flow and Tracer Transport[J]. Journal of contaminant hydrology,2009, 104(1/4): 4-35.

[13]ROSS P J,SMETTEM K R J.A Simple Treatment of Physical Non-equilibrium Water Flow in Soils[J].Soil Science Society of America Journal,2000,64(6):1926-1930.

[14]LEIJ F J, TORIDE N, FIELD M S,etal. Solute Transport in Dual-permeability Porous Media [J]. Water Resources Research, 2012, 48(4): 1-13.

[15]ARORA B, MOHANTY B P, MCGUIRE J T. Uncertainty in Dual Permeability Model Parameters for Structured Soils[J]. Water Resources Research,2012,48(1):1-17.

[16]TAYLOR P, ALAOUI A, GERMANN P,etal. Dual-porosity and Kinematic Wave Approaches to Assess the Degree of Preferential Flow in an Unsaturated Soil[J]. Hydrological Sciences Journal, 2003, 48(3): 37-41.

[17]DOLEŽAL F, ZUMR D, VACEK J,etal. Dual Permeability Soil Water Dynamics and Water Uptake by Roots in Irrigated Potato Fields[J]. František, Doležal, 2007, 62(5): 552-556.

[18]马东豪, 王全九. 土壤溶质迁移的两区模型与两流区模型对比分析[J]. 水利学报, 2004,35(6): 1-8.

[19]LU X, JIN M, VAN GENUCHTEN M T,etal. Groundwater Recharge at Five Representative Sites in the Hebei Plain, China[J]. Groundwater, 2011, 49(2): 286-294.

[20]吴庆华，张家发，蔺文静，等.土壤水流模式染色剂示踪及优先流程度评估[J]. 农业工程学报，2014，30(7)：82-90.

[21]吴庆华.人类活动影响下土壤水动态演变及其高效利用[D]. 北京：中国地质科学院， 2008：87.

[23]SIMMERS I. Groundwater Recharge: An Overview of Estimation Problems and Recent Developments[J]. London: Geological Society, Special Publications, 1998,(130):107-115.

(编辑：曾小汉)

收稿日期：2015-01-06; 修回日期：2015-02-06

基金项目：国家自然科学基金项目(51279016,41402213)；中国地质大学教育部长江三峡库区地质灾害研究中心开放性基金项目(TGRC201403)；中国地质科学院水文地质环境地质研究所开放性基金项目(KF201508)

作者简介：吴庆华(1981-)，男，湖北监利人，工程师，博士，主要从事包气带与地下水资源评价方面的研究，(电话)027-82820385(电子信箱)wqh0505@126.com。

通讯作者：张薇(1981-)，女，辽宁大连人，助理研究员，硕士，主要从事地下水资源与地热资源评价，(电话)0311-67598538(电子信箱)zhangwei1306@126.com。

doi:10.11988/ckyyb.20150012

中图分类号：P641

文献标志码：A

文章编号：1001-5485(2016)04-0016-06

Numerical Modeling of Groundwater Recharge Based on SoilWater Infiltrating: A Case Study of Luancheng Area in Hebei Province

WU Qing-hua1,2,3, WANG Gui-ling3, ZHANG Jia-fa1, ZHU Guo-sheng1, ZHANG Wei3

(1.Key Laboratory of Geotechnical Mechanics and Engineering of Ministry of Water Resources, Yangtze River Scientific Research Institute, Wuhan430010, China; 2.Three Gorges Research Center for Geo-hazard under Ministry of Education, China University of Geosciences, Wuhan430074, China; 3.Institute of Hydrogeology and Environmental Geology, Chinese Academy of Geological Sciences, Shijiazhuang050061, China)

Abstract:In order to investigate groundwater recharge in a long-term scale, soil water volume content of a soil profile of 340cm depth was observed for five years in Luancheng test site of Chinese Academy of Sciences. The dual-permeability model (e.g., matrix region and marcopore region) of Hydrus-1D containing parameter optimization procedure was applied to simulate the soil water movement and groundwater recharge. The place at 140cm depth rather than on the soil surface was chosen as the upper boundary, which could overcome the complexity and uncertainty of datum on the soil surface. The sensitivities of 17 parameters to groundwater recharge in the Hydrus-1D were analyzed, and the results showed the sensitivities of soil water hydraulic parameters nm,nF,αm and αF (subscript m and F represents soil matrix and fracture regions, respectively) and saturated soil hydraulic conductivity KsFwere the highest. These five parameters and other two parameters, i.e., Ka (effective hydraulic conductivity of fracture-matrix interface) and w (ratio of the volumes of the fracture domain and the total soil system) were chosen for the inversion. The modeling results showed that the modeled soil water volume content matched well to the measured values, with the correlation coefficient of 0.78. The groundwater recharge displayed similar character in each year of five years, e.g., the recharge was the largest in wet season, and then reduced gradually. The annual groundwater recharge was 220 mm/a, 211 mm/a of which attributed to the preferential flow, which indicated that the groundwater recharge was controlled by the preferential flow in this area. The results of this paper could be helpful to understand groundwater infiltration in a long-term scale, and could be useful to the management of groundwater resource and agricultural water saving.

Key words:soil water; groundwater; infiltration recharge; numerical modeling; Hydrus-1D

2016,33(04):16-21