一种分数域二分法LFM信号参数估计方法

孙　乐，魏　军，张衡阳，刘　立，王建翔

(1.空军工程大学 信息与导航学院，陕西 西安 710077；2.空军95801部队，北京 100076)



一种分数域二分法LFM信号参数估计方法

孙乐1，魏军1，张衡阳1，刘立1，王建翔2

(1.空军工程大学 信息与导航学院，陕西 西安 710077；2.空军95801部队，北京 100076)

摘要：针对传统基于分数阶傅里叶变换(fractional Fourier transform，FRFT)的线性调频(linear frequency modulated，LFM)信号参数估计方法中估计精度和计算量难以同时满足实际要求的问题，提出一种分数域二分法的LFM信号参数估计方法。该方法分析量化了变换阶次误差对参数估计误差的影响，利用单分量LFM信号变换阶次和分数域展宽的关系，通过迭代不断缩小变换阶次的取值范围，获得满足初设阈值的最优阶次，并利用最优阶次和峰值位置对LFM信号进行参数估计。采用逐次重构消除的方法，可以对强弱混合的多分量LFM信号进行参数估计。仿真结果表明，在满足信噪比要求的条件下，该方法能够有效地对LFM信号进行参数估计，可以通过参数估计精度的要求选择不同阈值，与传统方法相比，在参数估计精度相当的情况下大大地减小了计算量。

关键词：分数阶傅里叶变换；线性调频(LFM)信号；分数域；二分法；最优阶次

0引言

随着通信技术的发展，人们对通信系统的抗干扰性能提出了更高的要求。变换域通信系统以其独特的主动式抗干扰思想，受到了国内外大量学者的关注和研究。其抗干扰的关键在于对电磁频谱的准确估计，而线性调频(linear frequency modulation, LFM)干扰信号作为一种非平稳干扰信号，广泛地存在于实际应用中，因此，LFM信号参数的准确估计自然成为频谱估计的关键。

目前，许多国内外学者对LFM信号的参数估计做出了大量的研究，提出了一些可行的参数估计方法，它们大体可以总结为时频分析方法[1-3]和非时频分析方法[4-5]两类。但大部分方法都存在计算量大，估计精度低的问题，难以在工程实现中成熟运用。基于分数阶傅里叶变换(fractional Fourier transform，FRFT)的LFM信号参数估计，物理意义明确，多分量时没有交叉项干扰，时频聚集性能好，在众多估计方法中脱颖而出。在FRFT的基础上，文献[6]提出了一种预判的方法，该方法利用快速傅里叶变换(fast Fourier transformation，FFT)对LFM信号调频率进行预判，根据预判的结果再进行一维搜索，在保证参数估计精度的同时减小了计算量；文献[7]提出了基于自相关函数的参数估计方法，该方法利用分数阶自相关构造的检测统计量将参数估计的二维搜索变为阶次p的一维函数，进而进行参数估计，减小了运算的复杂度；文献[8]指出LFM信号的参数估计可以不受奈奎斯特采样定理的限制，提出了欠采样参数估计方法，该方法通过减小信号采样的点数降低参数估计的运算量。文献[9]提出了基于插值的参数估计，该方法利用较大步长对信号进行FRFT，得到变换阶次的粗略估计，在此基础上对变换阶次和分数域进行插值，得到了参数估计的精确值。以上方法虽然都可以有效地估计出LFM信号的参数，但大部分方法仍然需要在变换阶次一维搜索的基础上进行，并没有彻底解决估计精度和运算量之间的矛盾。

本文提出了一种基于分数域二分法的参数估计方法，根据变换阶次和分数域展宽的关系，通过分数域二分的方法不断迭代以缩小目标区域，最终找到满足设定阈值的变换阶次区域，取中值作为最优的变换阶次。相比其他方法，本文所提方法在保证参数估计精度的同时减少了计算量。

1FRFT定义及LFM信号参数估计原理

FRFT作为傅里叶变换的拓展形式，是一种新兴的时频分析工具。傅里叶变换可以理解为时域信号绕坐标原点旋转π/2后得到的表达形式，而FRFT可以理解为时域信号绕坐标原点旋转任意角度后得到的表达形式，这种特殊的性质使FRFT在信号处理时具有更好的灵活性。信号x(t)的α角度的FRFT定义为[10]

(1)

LFM信号的参数估计，实际上是寻找信号在分数域出现脉冲时的变换阶次和脉冲在分数域的位置，称此变换阶次为最优变换阶次。其参数估计的过程可以描述为[11]

(2)

(3)

可以看出，对LFM信号参数的估计可以转化为对LFM信号最优阶次和分数域峰值位置的估计，而峰值位置的估计首先要确定最优的变换阶次。但是实际估计时，最优变换阶次的估计是在一系列的离散值中选取，正是这种变换阶次的离散给参数估计的精度带来了巨大的影响。

2分数域二分法介绍

2.1最优变换阶次对参数估计的影响

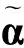
由(3)式可知，调频率的估计误差为

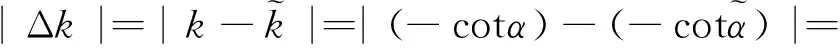
(4)

初始频率估计误差为

(5)

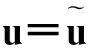
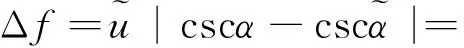
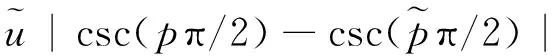
(6)

由(4)式和(6)式可以看出，调频率和初始频率的估计误差取决于cot函数和csc函数的性质，函数的斜率代表变换阶次误差对参数估计误差的影响程度。对cot(pπ/2)函数和csc(pπ/2)函数分别关于p求导，记为k(p)，f(p)，得

(7)

(8)

为了直观地看到阶次误差对参数估计误差的影响程度，图1给出了|k(p)|，|f(p)|随p变化的曲线图。

定义单位变换阶次误差对参数估计误差影响的大小为影响因子ξ，其物理意义为一倍变换阶次的误差将带来ξ倍的参数估计误差。ξ越大，参数估计精确度受变换阶次误差的影响越大；相反，ξ越小，参数估计精确度受变换阶次误差的影响越小。另外，记ξk,ξf分别为变换阶次误差对调频率和初始频率的影响因子。从图1可以看出，当变换阶次为1时，即信号调频率为0时，ξk为1.57，ξf为0，此时，变换阶次误差对参数估计误差的影响最小，随着变换阶次远离1的程度增大，即调频率绝对值的增大，ξk，ξf的值随着变换阶次的增大呈指数增长，当变换阶次为1.6时，ξk为4.54，ξf为3.67，这种误差在实际应用中是无法接受的。

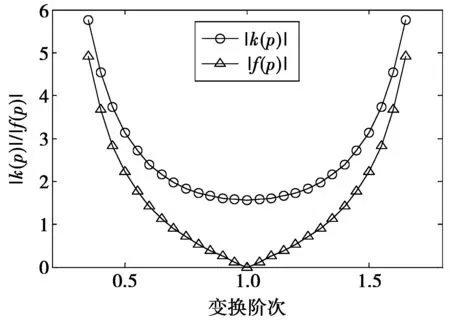
图1　|k(p)|，|f(p)|随p变化的曲线图Fig.1　Variation curve of |k(p)| and |f(p)| with p

2.2变换阶次和分数域展宽的关系

设LFM信号时长为T，信号时频线与t轴的夹角为β，则LFM信号的时频线长度ρ可表示为[14]

(9)

当分数域旋转角度为α时，LFM信号时频线相对于分数域u轴的夹角为θ=β-α，此时，LFM信号的分数域展宽为[14]

(10)

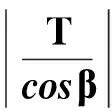
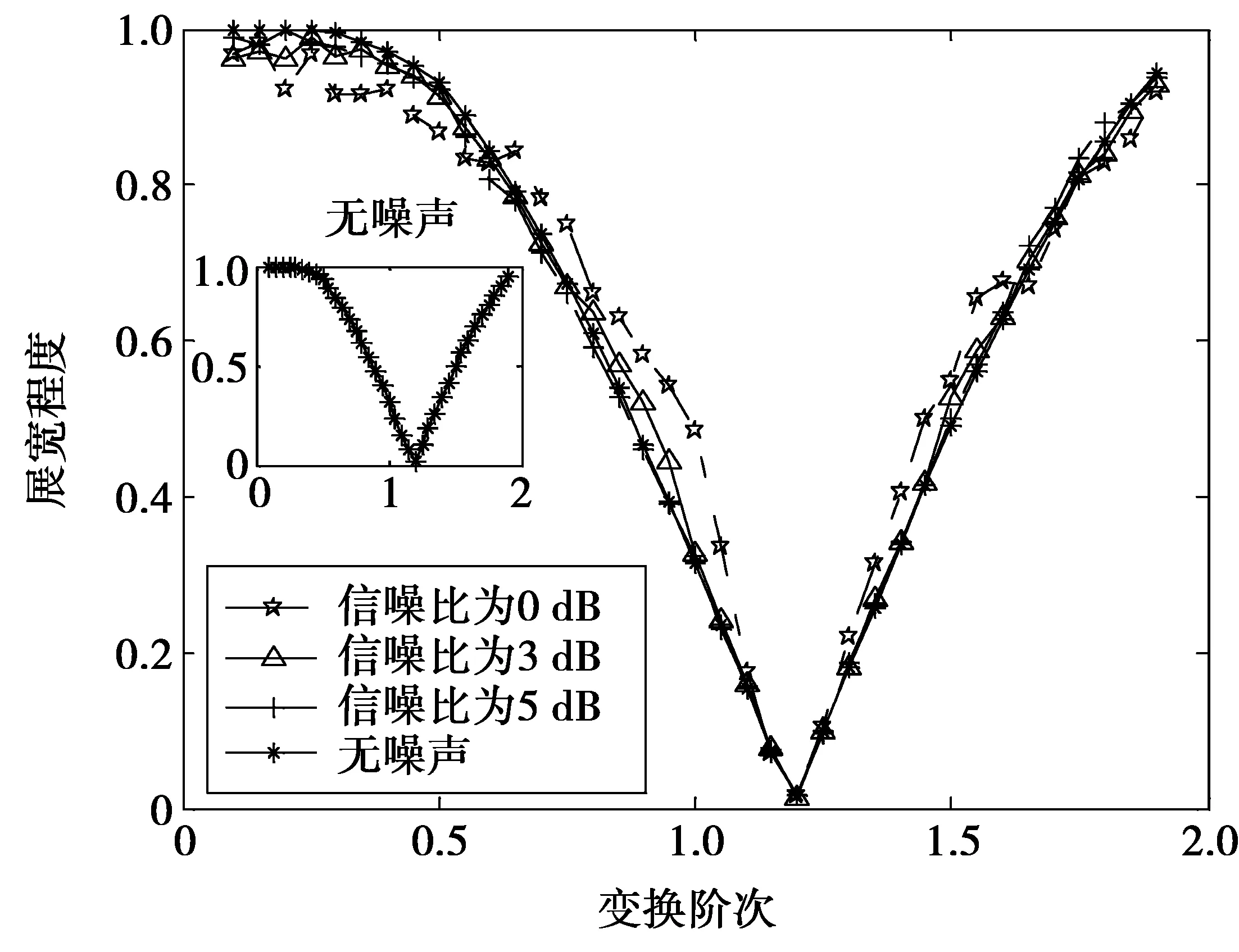
图2　不同信噪比下的分数域展宽程度Fig.2　Fractional domain bandspread under different SRN

从图2可以直观地看到以下3点。

1)LFM信号在最优阶次的分数域展宽最小，近似于0，而在最优阶次的两侧，其分数域的展宽程度呈准线性增长，且近似对称；

2)噪声会对分数域的展宽程度产生影响，而且信噪比越低，影响程度越严重；

3)变换阶次越接近最优阶次，噪声对分数域展宽程度的影响越小。

因此，可以利用LFM信号变换阶次和分数域展宽程度的关系，快速估计最优变换阶次的位置，进而对其参数进行估计。

2.3最优阈值的确定

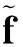
(11)

在参数估计时，阈值T的设定应满足在变换阶次达到阈值要求时，峰值位置唯一，即满足

(12)

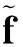
(13)

2.4基于分数域二分法的参数估计算法流程

最优变换阶次的精确估计是整个参数估计工作的第一步，本节利用变换阶次和分数域展宽的关系，介绍分数域二分法的参数估计方法，其过程如图3所示。

图3　分数域二分法参数估计过程Fig.3　Parameter estimation process of fractional domain dichotomy

具体步骤如下。

1)设变换阶次的2个初始值p1和p2；

2)对待估计信号进行p1和p2阶FRFT，并分别计算出对应的分数域展宽a1和a2；

4)比较a1，a2，a的大小，取其中较小的2个值所对应的变换阶次为新的初始值；

5)如果2个初始值之差小于预设的阈值T，进行第6)步；否则，返回第2)步；

7)对待估计信号进行p阶FRFT，并得到峰值位置u，利用p和u对参数进行估计，算法结束。

在计算分数域展宽的时候，该方法对其分数域幅值进行平滑处理，减小了噪声对展宽的影响。

上述算法可以总结为一个通过不断迭代寻找分数域最小展宽的过程。对于多分量LFM信号，依然可以用上述算法对其参数进行估计。具体方法如下，对待估计信号进行上述算法，通过迭代，必然可以得到分数域展宽最小的一种情况，此时，对应的变换阶次为某一分量的最优阶次，利用其最优阶次和峰值位置，可以估计出这一分量的信号参数，然后重构此信号并在待估计信号中减去此信号，对剩余信号重新进行上述方法，依此不断重复，直到剩余信号的分数域展宽均大于0.5，则多分量LFM信号的参数被全部估计。

3仿真分析

3.1计算量分析

采用分数域二分法对LFM信号参数进行估计时，运算量主要是对每次迭代的初始值和中值进行FRFT。假设待估计LFM信号的调频率绝对值最大为50 Hz/s，根据本文仿真参数设置，变换阶次初始值可设置为0.36和1.64，最优阈值为0.001 5，则采样点数为N的单分量LFM信号参数估计迭代次数为11次，一共需要进行12次FRFT，采用Ozaktas采样型算法，计算量为O(12NlogN)。而对于搜索步长为γ的传统二维搜索算法，每一分量的参数估计都需要进行变换阶次的二维搜索，其计算量为O(2NlogN/γ)，在本文仿真参数设置下，γ分别取0.01和0.001，其计算量分别为O(200NlogN)和O(2 000NlogN)，可以看出，本文方法在计算量方面具有明显的优势。 利用本文方法对多分量LFM信号进行参数估计，对每一分量都需要进行12次FRFT， 如果分量较多时，该方法的估计效率会有所下降。

3.2单分量LFM信号参数估计仿真

仿真参数设置：LFM信号的时间取值为[-2，2]，采样频率fs为128 Hz，采样点数为512，变换阶次的2个初始值分别为0.36和1.64，初始频率f0为10 Hz，初始相位为0 rad，调频率k取8 Hz/s。变换阶次为初始值时，不同信噪比下的分数域展宽如图4，图5所示。

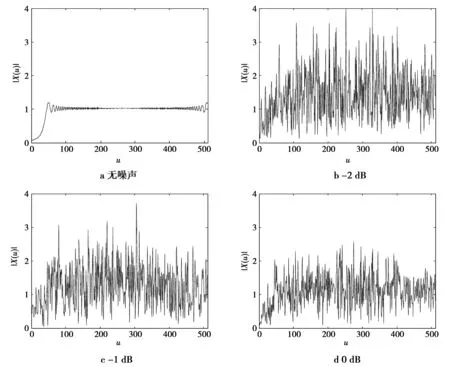
图4　初始值为0.36时不同信噪比下的分数域展宽Fig.4　Fractional domain bandspread with initial value 0.36 under different SRN

由图4、图5可以看出，在信噪比为-2 dB时，待估计信号的分数域展宽遭到严重破坏，难以对分数域展宽做出准确计算，此时，参数估计误差较大；随着信噪比的增加，其分数域展宽越来越清晰，正确计算展宽的概率不断增加，参数估计的误差也随之减小；当信噪比增大到0 dB时，可以容易地计算展宽并进行比较。

在变换域通信系统幅度谱生成时，LFM信号是作为干扰信号出现，干噪比大于0 dB，因此，不会对文中方法分数域展宽的计算产生影响，可以稳定地进行参数估计。

对不同的信噪比和阈值，分别进行100 000次仿真，调频率和初始频率的均方误差仿真结果如图6所示。

从图6可以看出以下3点。

1)对于传统二维搜索的参数估计方法，减小步长可以增加调频率和初始频率的估计精度。随着信噪比的增加，其参数估计的误差不断减小，且趋于稳定；

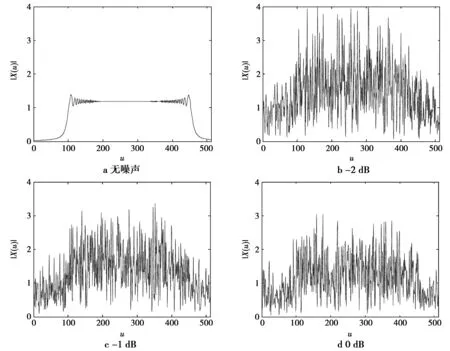
图5　初始值为1.64时不同信噪比下的分数域展宽Fig.5　Fractional domain bandspread with initial value 1.64 under different SRN

图6　不同信噪比下参数估计均方误差分析Fig.6　MSE analysis of parameter estimation under different SRN

2)当信噪比大于0 dB时，随着信噪比的增加，文中方法可以稳定地对信号进行参数估计；在最优阈值时，可以达到与传统方法相当的精度。在信噪比小于0 dB时，文中方法相比传统二维搜索方法性能衰减速度加快，但此时LFM信号能量较小，不会影响通信系统的性能；

3)在信噪比满足的情况下，减小设定的阈值，可以提高变换阶次的估计精度，进而提高参数估计的精度；但当设定的阈值达到最优阈值后，阈值的减小不会换来参数估计精度的显著提高。

3.3多分量LFM信号参数估计仿真

仿真参数设置：待估计信号取二分量LFM信号，时间取值、采样频率、采样点数、变换阶次的初始值与3.2节中相同。信噪比为3 dB，初始频率分别为-6 Hz，16 Hz，调频率分别为6 Hz/s，16 Hz/s，初始相位都为0 rad，利用分数域二分法对待估计信号进行参数估计。

设定阈值为最优阈值0.001 5，经过一次参数估计，LFM信号的最优阶次估计值为1.294 4，调频率估计值为16.012 8，初始频率估计值为15.945 5，对待估计信号做最优阶次的FRFT如图7a所示。在待估计信号中剔除估计出来的单分量LFM信号，重复上述过程，可以估计出LFM信号的第2分量的最优阶次为1.118 1，调频率估计值为6.030 3，初始频率估计值为-6.115 6，对其进行最优阶次的FRFT如图7b所示。

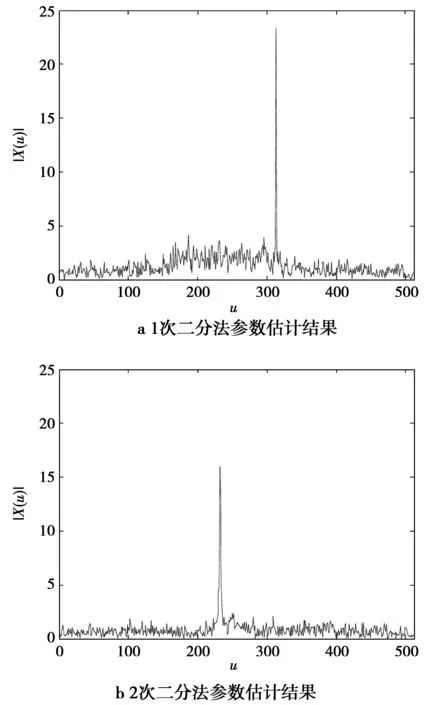
图7　二分量LFM信号二分法参数估计Fig.7　Parameter estimation of 2-component LFM signal using Fractional domain dichotomy

采用分数域二分法对多分量LFM信号进行参数估计时，不需要考虑强弱信号遮蔽问题的影响，但是在分量较多时，估计误差的叠加将导致估计的精度将有所下降。

综上所述，分数域二分法可以利用较小的计算量精确的估计出LFM信号的参数。

4结论与展望

提出了一种分数域二分法的快速精确参数估计方法，该方法利用变换阶次和分数域展宽的关系，通过迭代，获得对应分数域展宽最小的变换阶次，作为最优的变换阶次，最终利用最优变换阶次和峰值位置进行参数估计。在信噪比满足的情况下，保证估计精度的同时大大地减小了计算量。通过在不同信噪比和阈值下进行仿真，验证了方法的有效性，同时可以对多分量LFM信号进行参数估计。该方法改进了最优阶次的估计精度，但是对峰值位置的确定仍然受到分数域分辨率的影响，导致初始频率的估计精度受到限制，这是下一步需要深入研究和解决的问题。

参考文献：

[1]TAO Ran, DENG Bing, WANG Yue. Research progress of the fractional Fourier transform in signal processing [J]. Science in China-Series F: Information Science, 2006, 49(1): 1-25.

[2]ZHANG Long,HE Xiaohui,XING Mengdao,et al.Parameters estimation of LFM signals based on STTFD[C]//IEEE.Signal Processing,2008 16th European Conference on.Lausanne,Switzerland:IEEE,2008:2351-2355.

[3]YUAN Ye, LI Qingfu, FU Ying. Detection and parameter estimation of multicomponent LFM signals based on Hilbert-Huang hough transform[C]//IEEE.Computational Intelligence and Industrial Applications，2009 Asia-Pacific Conference on.Wuhan,China:IEEE,2009:476-479.

[4]唐鹏飞, 林钱强，袁斌，等. 基于积分二次相位函数和分数阶Fourier变换的多分量 LFM信号参数估计[J].信号处理,2012, 28(7): 926-931.

TANG Pengfei, LIN Qianqiang, YUAN Bin, et al. Parameter estimation of multi-component LFM signals using integrated quadratic phase function and Fractional Fourier transform[J].Signal Processing,2012,28(7):926-931.

[5]刘昊晨, 梁红. 线性调频信号参数估计和仿真研究[J]. 计算机仿真, 2011, 28(2): 157-159, 263.

LIU Haochen, LIANG Hong. The parameter estimation and simulation research of LFM signal[J].Computer Simulation, 2011, 28(2): 157-159, 263.

[6]张希会, 蔡竞业, 杨亦师. 基于分数阶傅里叶变换的LFM信号参数估计预判法[J]. 信号处理, 2008, 824(4): 667-671.ZHANG Xihui,CAI Jingye,YANG Yishi.The Pre-estimation algorithm of chirp based on the Fractional Fourier transform[J].Signal Processing,2008,824(4):667-671.

[7]王璞, 杨建宇, 杜雨洺. 分数阶自相关和FRFT的LFM信号参数估计[J]. 电子科技大学学报, 2006, 35(2): 179-182.WANG Pu,YANG Jianyu,DU Yuming.Parameter estimation of LFM signal using Fractional autocorrelation and FRFT[J].Journal of UEST of China,2006,35(2):179-182.

[8]仇兆炀, 陈蓉, 汪一鸣. 基于FRFT的线性调频信号欠采样快速检测方法[J].电子学报, 2012, 40(11): 2165-2170.QIU Zhaoyang,CHEN Rong,WANG Yiming.Fast detection of LFM signal based on FRFT and sub-Nyquist sampling[J].Acta Electronica Sinica,2012,40(11):2165-2170.

[9]SONG Jun, LIU Yunfei. Parameter estimation of LFM signal by direct and alpine interpolation based on FRFT[C]//Information technology and software engineering, 2012 international conference on. Beijing, China: Springer, 2012: 41-48.

[10] 陶然, 邓冰, 王越. 分数阶傅里叶变换及其应用[M]. 北京: 清华大学出版社, 2009: 13-46.

TAO Ran, DENG Bing, WANG Yue. Fractional Fourier transform and its applications[M]. Beijing: Tsinghua University Press, 2009: 13-46.

[11] QI Lin, TAO Ran, ZHOU Siyong, et al. Detection and parameter estimation of multicomponent LFM signal based on Fractional Fourier transform[J]. Science in China: Ser F Information Sciences, 2004, 47(2): 184-198.

[12] OZAKTAS H M, ARIKAN O, KUTAY M A, et al. Digital computation of the Fractional Fourier transform[J]. IEEE Trans Signal Processing,1996,44(9):2141-2150.

[13] 赵兴浩, 邓兵, 陶然. 分数阶傅里叶变换数值计算中的量纲归一化[J]. 北京理工大学学报, 2005, 25(4): 360-364.

ZHAO Xinghao, DENG Bing, TAO Ran. Dimensional normalization in the digital computation of the fractional Fourier transform[J]. Transactions of Beijing Institute of Technology, 2005, 25(4): 360-364.

[14] 徐会法, 刘峰. 线性调频信号分数阶频谱特征分析[J].信号处理, 2010, 26(12): 1896-1901.

XU Huifa,LIU Feng.Spectrum characteristic analysis of linear frequency-modulated signal in the fractional Fourier domain[J].Signal Processing,2010,26(12):1896-1901.

DOI：10.3979/j.issn.1673-825X.2016.04.006

收稿日期：2015-06-19

修订日期：2016-04-07通讯作者：孙乐sunle202@163.com

基金项目：国家自然科学基金(61202490)；航空科学基金(2013ZC15008)

Foundation Items：The National Natural Science Foundation of China(61202490); The Aeronautical science Foundation of China(2013ZC15008)

中图分类号：TN911.7

文献标志码：A

文章编号：1673-825X(2016)04-0473-08

作者简介：

孙乐(1991-)，男，陕西澄城人，硕士研究生，主要研究领域为变换域通信系统。E-mail: sunle202@163.com。

魏军(1968-)，男，陕西西安人，副教授，硕士生导师，主要研究领域为航空数据链。

张衡阳(1978-)，男，湖南祁东人，副教授，硕士生导师，主要研究领域为航空自组网与数据链。

刘立(1990-)，男，陕西华县人，硕士研究生，主要研究领域为变换域通信系统。

王建翔(1979-)，男，陕西阎良人，主要研究领域为信息通信工程。

(编辑：王敏琦)

Fractional domain dichotomy LFM signal parameter estimation method

SUN Le1, WEI Jun1, ZHANG Hengyang1, LIU Li1, WANG Jianxiang2

(1. Information and Navigation College, Air Force Engineering University, Xi’an, 710077, P.R.China;2. Air Force 95801 Army, Beijing 100076，P.R.China)

Abstract:Traditional parameter estimation methods of linear frequency modulation(LFM) signal based on fractional fourier transform did not deal with the contradiction between the satisfactory precision and the lesser computation cost . Therefore, a fractional domain dichotomy is proposed in this paper. Firstly, the effect of the transform order error on the parameter estimation error is analyzed and quantified. Then, the fractional domain dichotomy is adopted to obtain the optimal order of single component LFM signal corresponding to fractional domain minimum bandspread. Finally, the parameters are estimated according to the optimal order and the peak position. The parameters of strong and weak mixing multi-component LFM signal are estimated by using successive reconstruction and elimination method. Simulation results show that, compared with the traditional method, the method can meet the requirement of estimation precision with the computation cost reduced significantly.

Keywords：fractional Fourier transform; linear frequency modulated(LFM) signal; fractional domain; dichotomy; the optimal order