工程用高聚物注塑成型制品服役应力优化设计

王新宇，李　征，谷俊峰，阮诗伦,2，申长雨,2，王希诚,2



工程用高聚物注塑成型制品服役应力优化设计

王新宇1，李征1，谷俊峰1，阮诗伦1,2，申长雨1,2，王希诚1,2

（1大连理工大学工程力学系，辽宁 大连 116024；2大连理工大学工业装备结构分析国家重点实验室，辽宁 大连 116024）

摘要:近年来，航空航天、汽车等工程领域大量使用工程用高分子聚合物材料制备结构零部件。在复杂的工作环境下，工程用高聚物注塑成型零部件承受机械荷载、热荷载等服役条件，其服役应力的大小直接关系到工程设备的结构安全。将半球形聚碳酸酯(PC)制品的翘曲变形和残余应力作为服役的初始条件，建立考虑制品结构、模具结构以及工艺条件的服役应力优化模型，利用基于Kriging代理模型和EI加点法的序列优化方法，有效地降低了半球形聚碳酸酯制品的服役应力。结果表明，制品厚度、熔体温度和保压压力对服役应力影响较大。

关键词:聚合物加工；服役应力；Kriging模型；优化设计；产品设计

引 言

由于工程高分子聚合物材料具有耐高温、耐腐蚀、比强度高等优异的性质，汽车行业、航空航天、海洋工程等工程领域已开始广泛使用工程用高聚物材料制品。工程高分子材料注塑成型制品在应用中承受复杂的荷载条件（如高温、高压、碰撞等），其内部的服役应力影响着设备结构和人身的安全。因此，从制品成型角度，研究如何减小工程高聚物零部件的最大服役应力有着非常重要的现实意义。

注塑成型过程不可避免地会带给制品一定程度的成型缺陷。国内外学者有大量的关于注塑成型缺陷的研究，目的在于通过优化工艺参数、模具结构等因素解决制品的成型缺陷，提高制品的加工质量。例如，Mathivanan等[1]、Guo等[2]研究了制品的沉降斑问题，Deng等[3]、Ozcelik[4]分别解决了制品熔接痕问题。其中，关于制品的翘曲变形和残余应力的优化研究工作最多。Kurtaran等[5]采用响应面结合遗传算法的优化策略降低了制品的翘曲变形。Gao等[6-7]、周香等[8]利用Kriging代理模型的方法优化了成型工艺参数，降低了制品的翘曲变形。Kitayama等[9]通过优化保压压力曲线减小了制品的翘曲变形，提高了制品的成型质量。Wang等[10]则通过优化动态注塑工艺参数，降低制品的最大翘曲值。此外，刘文娟等[11]分别对常速率注射参数和曲线式速率注射参数进行优化设计，目的在于降低制品的成型残余应力。

制品从成型到服役经历了注塑成型加工、与适配结构装配和承受载荷服役3个过程，成型加工造成的翘曲变形和残余应力导致其在装配后会产生较大的装配应力，进而降低制品的服役承载能力。因此，制品的翘曲变形与残余应力在其装配与承载过程中是不可忽略的。但是，很少有文献真实地考虑翘曲变形与残余应力对制品装配和承载服役应力的影响，并进行相关的优化工作。

本文将翘曲变形和残余应力结果作为结构装配和承载服役分析的位移条件和初始应力条件，建立了以注塑成型工艺条件、制品厚度和冷却管道直径为优化设计变量、服役应力为目标函数的优化模型，利用基于代理模型的序列优化方法有效地降低了制品的服役应力。这种从制造到服役的一体化分析与优化策略充分考虑了成型加工因素对服役应力的影响，可以作为工程塑料制品成型设计的有效数值分析方法。值得注意的是，本文提出的策略充分考虑了制品自身结构上的设计参数，可以在优化工艺参数和模具结构参数的同时进行制品结构上的几何设计，为工程塑料注塑成型零部件的尺寸设计提供了有效且全面的优化设计方法。

1　制造-服役的分析方法

考虑成型缺陷的工程高聚物制品从成型到服役一体化分析方法如下述步骤。

（1）建立模型。利用CAD软件建立目标制品的几何结构，划分有限元网格。

（2）成型分析。将制品有限元模型导入Moldflow insight 2016，设置相关成型工艺参数，对制品进行注塑成型模流分析，获取制品成型后的翘曲变形与内部残余应力结果。

（3）装配分析。以残余应力为制品结构的初始内应力，以装配位置翘曲变形值的大小作为装配条件，装配方向为翘曲变形的反方向，利用 ANSYS进行制品装配分析。

（4）服役分析。对装配后的制品结构施加荷载工况（如均布荷载、温度荷载等），利用ANSYS进行结构的力学分析，提取最大的工作应力。

上述过程建立了成型条件与服役应力的联系。选取制品结构、模具结构以及工艺条件相关参数作为设计变量，结合一定的优化方法，可以从工程设计的角度降低制品的服役应力。

图1　半球形PC制品与模具结构Fig.1 Depicture of hemisphere polycarbonate part and mould construction

2　半球形聚碳酸酯应力优化问题

半球形PC制品和模具结构如图1所示，其中制品下边界为装配边界，翘曲的制品被强制装配到刚性结构上，服役条件为内表面承受0.1 MPa压力，工作温度为-40℃。成型材料为SABIC 生产的PC Lexan 105，表1列出了其基本的物性参数。

表1　SABIC Lexan 105聚碳酸酯材料物性Table 1 Properties of SABIC Lexan 105 polycarbonate

制品直径为100 mm，包含9696个三角形单元，选取制品厚度(h)为设计变量，目的在于寻找合理的制品结构以降低最大服役应力，并研究制品厚度参数对服役应力的影响。冷却管道采用隔水板式随形水道，隔水板直径(D)选为设计变量。此外，选取熔体温度（Tmelt）、成型时间（tmolding）、注射时间（tfilling）、保压压力百分比（P）、保压时间（tpacking）5个主要的工艺参数为设计变量。设计变量取值范围如表 2所示。其中，熔体温度取值范围为Moldflow材料测试推荐的加工温度范围，其他变量取值范围按经验给出。其中保压压力采取图2所示梯形压力曲线，设计变量中的保压时间为恒压段作用时间。服役应力优化模型为

其中，σMises为制品注塑成型装配后承载的Mises应力，Ωx为表2构成的超立方变量设计空间。

表3　设计变量取值范围Table 2 Rang of design parameters

图2　梯形保压曲线Fig.2 Trapezoid packing pressure curve

3　基于代理模型的序列优化方法

3.1 Kriging代理模型

工程优化问题的目标函数与设计变量之间不是显式的函数关系，需要结合插值方法建立近似的函数关系[12-13]。本文采用 Kriging代理模型建立目标函数与设计变量的预测模型[14]。其表达式为

其中，误差项ε（x）服从高斯分布norm[0,σ2]。Kriging均值模型的预测均值与预测方差分别为[15]

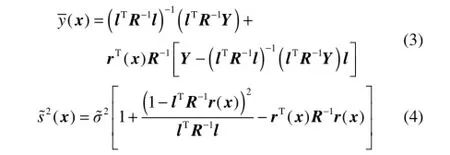
其中，li=1,Y为插值样本的目标函数值向量，2σ~ 为σ2的最大似然估计，r为未知空间点与已知样本点的相关函数向量，R为已知k个样本点之间的相关函数矩阵。本文采用高斯相关函数，其定义为

其中，θn为第n维变量的相关系数，代表了目标函数关于设计变量的非线性程度，用于描述目标函数关于变量xn的敏感程度，θn越大，目标函数关于第n维变量xn非线性程度越大，意味着xn微小变化会引起目标函数非常大的变化。

3.2 EI加点序列优化方法

根据Kriging插值模型的随机特征，可以定义“提高”函数与EI函数[16]

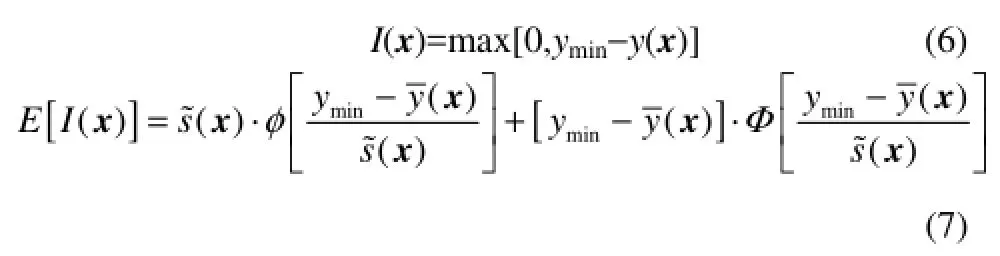
其中，ymin为当前插值样本中的最小函数值，ϕ 和Φ分别表示标准正态分布的密度函数和分布函数。

根据EI函数的数学意义，可以发现最大EI函数值能够提供 Kriging模型中比当前样本集最优值更优的设计点或者插值模型预测不确定性较大的点。基于Kriging模型和EI函数发展的序列优化方法能够快速有效地进行工程优化设计[17-19]。优化问题（1）式转变为如下等效的优化模型列示

实现式（8）优化过程的具体方法如下所述:

（1）采取一定的初始样本取样方法，在设计域内抽取一定数量的初始样本X，与目标函数值Y；

（2）利用样本集建立初始 Kriging代理模型式（2），进而得到EI函数式（7）；

（3）结合一定的优化算法（如序列二次规划、遗传算法、粒子群算法等，本文采用序列二次规划法SQP）搜索取最大EI函数值的x*，计算其对应目标函数y*，判断收敛条件是否满足。若满足，则停止优化。否则，将[x*, y*]添加到X和Y中，执行步骤（2）～步骤（3），直到收敛条件满足为止。

每次寻找最大 EI值都是寻找一个能够比当前样本最优值更好的设计点，或插值模型最不确定的设计点。因此，基于Kriging模型和EI函数的优化问题(8)是一个不断寻找最大“提高”可能性的过程。

4　优化结果与讨论

4.1 优化结果

采用Georgiou等[20]提出的取样方法选取32个正交拉丁超立方样本建立初始Kriging模型，其中样本最优结果为42.26 MPa。优化结果如表3所示，Mises应力云图如图3所示。优化结果最大服役应力为37.13 MPa，比初始样本中最优设计的最大服役应力结果下降12.14%。其中，保压压力达到取值的上界，熔体温度也十分接近取值的上界，而制品厚度达到取值下界。这意味着在给定的设计空间中，提高保压压力和熔体温度、减小制品厚度均有利于降低最大服役应力。

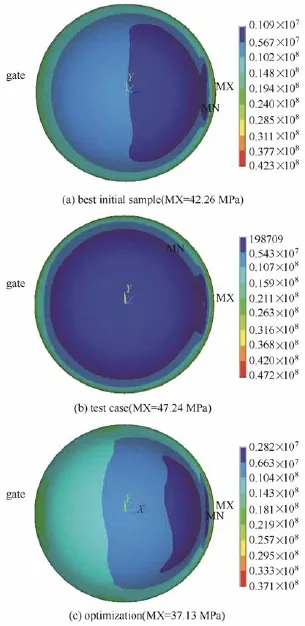
图3　样本最优、测试算例和优化结果服役应力对比Fig.3 Comparison on service stress between the best sample design and the optimum design

选取厚度为2 mm、隔水板直径为25 mm的测试算例设计，采用优化结果相同的工艺条件，进行服役分析（表3）。最大服役应力为47.24 MPa，优化设计比其小21.4%。说明制品和模具结构对服役应力同样有很大的影响。因此，对比结果进一步说明了对工艺条件、制品结构、模具结构同时进行整体性的优化设计，对降低服役应力是十分必要的。尤其是对于具有特征结构（如筋、孔、槽等）的工程塑料制品，优化模型中需要充分考虑特征结构的几何设计参数，这样的优化模型能够针对服役应力进行更全面的制品几何尺寸设计，从而减小制品内部的最大服役应力（或者应变），提高其承受载荷的能力，提升服役质量。对于本算例，特征尺寸为厚度，关于厚度对服役应力影响的讨论详见4.2节相关的内容。

图4　变量相关系数Fig.4 Correlative coefficients of design factors

4.2 结果讨论

如前所述，Kriging代理模型中的相关系数 θn代表了代理模型与第n维设计变量之间的非线性程度。θn值越大，意味着变量相关区域越小，变量的空间相关性越小，模型关于该变量的非线性程度越高，也即目标函数对该变量比较敏感，变量很小的变化可能会引起目标函数很大的改变。优化结果的相关系数如图4所示。从图4可以看出，服役应力关于制品厚度的非线性程度要高于其他设计变量。对于工艺条件来说，服役应力关于保压压力的非线性程度最大，其次是熔体温度，关于保压时间的非线性程度最小。

表3　应力优化结果Table 3 Optimization result of service stress

图5　不同载荷条件下无成型缺陷制品的厚度与服役应力的关系Fig.5 Relationship between thickness of perfect-molded part and service stress under different load conditions

图6　服役应力与翘曲变形和残余应力之间的关系Fig.6 Relationship between service stress and warpage/residual stress

从成型加工的角度来说，制品的厚度是决定制品成型加工条件的最重要的一个因素。对于相同结构的制品来说，厚度越小，其壁面剪切黏度越大，注射压力越大，越容易引起较大的流动残余应力和翘曲变形。因此，较厚的制品有利于成型加工。但是，从服役的角度来说，制品承受的温度荷载与结构体积相关，在相同低温条件、一定的厚度范围内，厚壁制品较薄壁制品收缩明显，容易导致较大的温度应力。因此，较薄的制品有利于降低温度应力。制品同时承受了均布荷载，制品越厚，刚度越大，有利于承受机械载荷，抵抗变形，降低服役应力。图5为无翘曲无残余应力状态下制品厚度与服役应力的关系。由于没有装配应力，其内部应力是承载的服役应力。从图5中可以看出机械应力要比温度应力小很多。优化的方向应是制品温度应力减小的方向。因此，结果中厚度优化到了下界是合理的。

保压压力的大小和保压时间的长短决定了制品的体收缩率大小。不均匀的收缩易导致不可接受的翘曲变形。熔体温度是另外一个影响成型质量非常重要的因素。较低的熔体温度导致制品内部产生较大的剪切应力，形成较大的流动残余应力。提升熔体温度有利于提高熔体流动性，减少制品的翘曲变形和残余应力。此外，较短的充填时间容易导致浇口处产生较高的剪切应力。较短的成型时间可以缩短成型周期，提高生产效率。但是，过短的冷却时间容易导致制品冷却不彻底，脱模后收缩严重。

服役应力与翘曲变形和残余应力的关系如图 6所示。从整体趋势来说，减小翘曲变形和残余应力有利于减小服役应力。但是，服役应力是成型缺陷、装配条件和服役条件共同作用的结果。由于翘曲变形和残余应力无法避免，因此，以服役应力为目标函数的优化问题实际上是寻找翘曲变形和残余应力最优组合的制品结构设计和注塑成型工艺与模具设计方案。

4.3 可行设计空间

基于Kriging代理模型和EI加点法的序列优化方法目的在于寻找可行域内的最优设计。但是，对于注塑成型研究者来说，成型缺陷和服役应力是无法避免的。因此，在目标函数值可接受的条件下，为工程师提供一组可行的设计窗口具有非常实际的现实意义，工程师可以根据自己的需求选取合适的设计方案。从加点寻优历史图7中可以发现，其中很多设计方案的目标函数值都接近最优设计。例如，本文表4给出了9组设计方案，其服役应力均在40 MPa以内。

图7　EI加点寻优历史Fig.7 Iteration for searching optimum with EI method

表4　推荐设计方案Table 4 Recommended design schemes

5　结 论

从制品、模具和工艺的整体设计角度，本文建立了服役应力的工程优化模型，利用基于 Kriging代理模型和EI加点法的序列优化方法，有效地降低了半球形PC制品的服役应力。结论如下。

（1）成型缺陷（如翘曲变形、残余应力）能够降低制品的服役质量。因此，在对工程高聚物注塑制品进行结构分析时，要充分考虑成型缺陷的影响，尤其是残余应力。

（2）减小翘曲变形与残余应力能够降低服役应力，但是服役应力是成型质量、装配条件以及服役工况共同作用的结果。由于成型缺陷不可避免，因此寻找一个合理的缺陷状态是降低服役应力的有效途径。

（3）通过分析变量对目标非线性程度的影响发现，制品厚度、保压压力和熔体温度对服役应力的影响较大。说明工程高聚物注塑制品厚度与工艺的设计对其承载服役质量至关重要。因此，降低服役应力应充分考虑结构和工艺两方面因素。

本文提出的成型-服役一体化优化设计策略具有非常好的通用性，对工程高分子材料注塑成型制品的产品设计具有非常重要的实际意义。

References

[1] MATHIVANAN D, PARTHASARATHY N S. Sink-mark minimization in injection molding through response surface regression modeling and genetic algorithm [J]. Int. J. Adv. Manuf. Tech., 2009, 45 (9/10): 867-874.

[2] GUO W, HUA L, MAO H J. Minimization of sink mark depth in injection-molded thermoplastic through design of experiments and genetic algorithm [J]. Int. J. Adv. Manuf. Tech.,2014, 72 (1/2/3/4): 365-375.

[3] DENG Y M, ZHENG D, SUN B, et al. Injection molding optimization for minimizing the defects of weld lines [J]. Polym-Plast Technol., 2008, 47 (9): 943-952.

[4] OZCELIK B. Optimization of injection parameters for mechanical properties of specimens with weld line of polypropylene using Taguchi method [J]. Int. Commun Heat Mass, 2011, 38 (8): 1067-1072.

[5] KURTARAN H, ERZURUMLU T. Efficient warpage optimization of thin shell plastic parts using response surface methodology and genetic algorithm [J]. Int. J. Adv. Manuf. Tech., 2006, 27 (5/6): 468-472.

[6] GAO Y H, WANG X C. An effective warpage optimization method in injection molding based on the Kriging model [J]. Int. J. Adv. Manuf. Tech.,2008, 37 (9/10): 953-960.

[7] GAO Y H, WANG X C. Surrogate-based process optimization for reducing warpage in injection molding [J]. J. Mater. Process Tech., 2009, 209 (3): 1302-1309.

[8] 周香, 陈文琳, 王晓花, 等. 基于 Kriging代理模型和遗传算法的注塑件翘曲优化 [J]. 塑性工程学报, 2015, (2): 142-147.

ZHOU X, CHEN W L, WANG X H, et al. Warpage optimization for injection molding based on Kriging model and genetic algorithms [J]. Journal of Plasticity Engineering, 2015, (2): 142-147.

[9] KITAYAMA S, ONUKI R, YAMAZAKI K. Warpage reduction with variable pressure profile in plastic injection molding via sequential approximate optimization [J]. Int. J. Adv. Manuf. Tech., 2014, 72 (5/6/7/8): 827-838.

[10] WANG X Y, GU J F, SHEN C Y, et al. Warpage optimization with dynamic injection molding technology and sequential optimization method [J]. Int. J. Adv. Manuf. Tech., 2015, 78 (1/2/3/4): 177-187.

[11] 刘文娟, 王新宇, 李征, 等. 基于 Kriging代理模型的注塑件残余应力优化分析 [J]. 塑料工业, 2015, (1): 53-57.

LIU W J, WANG X Y, LI Z, et al. Residual stress optimization of injection-molded parts based on Kriging surrogate model [J]. China Plastics Industry, 2015, (1): 53-57.

[12] DEBOOR C, RON A. Computational aspects of polynomial interpolation in several variables [J]. Math. Comput., 1992, 58 (198): 705-727.

[13] HUANG D, ALLEN T T, NOTZ W I, et al. Sequential Kriging optimization using multiple-fidelity evaluations [J]. Struct. Multidiscip. O., 2006, 32 (5): 369-382.

[14] CRESSIE N. The origins of Kriging [J]. Math. Geol., 1990, 22 (3): 239-252.

[15] SACKS J, WELCH W J, MITCHELL T J, et al. Design and analysis of computer experiments [J]. Statistical Science, 1989, 4 (4): 409-423.

[16] JONES D R, SCHONLAU M, WELCH W J. Efficient global optimization of expensive black-box functions [J]. J. Global Optim., 1998, 13 (4): 455-492.

[17] SHI H Z, GAO Y H, WANG X C. Optimization of injection molding process parameters using integrated artificial neural network model and expected improvement function method [J]. Int. J. Adv. Manuf. Tech., 2010, 48 (9-12): 955-962.

[18] SOBESTER A, FORRESTER A I J, TOAL D J J, et al. Engineering design applications of surrogate-assisted optimization techniques [J]. Optim. Eng., 2014, 15 (1): 243-265.

[19] SUN G Y, SONG X G, BAEK S, et al. Robust optimization of foam-filled thin-walled structure based on sequential Kriging metamodel [J]. Struct. Multidiscip. O., 2014, 49 (6): 897-913.

[20] GEORGIOU S D, STYLIANOU S. Block-circulant matrices for constructing optimal Latin hypercube designs [J]. Journal of Statistical Planning and Inference, 2011, 141 (5): 1933-1943.

2015-12-07收到初稿，2016-03-17收到修改稿。

联系人:谷俊峰。第一作者:王新宇（1986—），男，博士研究生。

Received date: 2015-12-07.

中图分类号:TQ 320.66

文献标志码:A

文章编号:0438—1157（2016）07—3040—07

DOI:10.11949/j.issn.0438-1157.20151843

基金项目:国家重点基础研究发展计划项目（2012CB025905）；国家自然科学基金重点项目（11432003）；111引智计划项目（B14013）；国家高技术研究发展计划项目（2015AA033803）。

Corresponding author:GU Junfeng, jfgu@dlut.edu.cn supported by the National Basic Research Program of China (2012CB025905), the National Natural Science Foundation of China (11432003), the 111 Project of China (B14013) and the National High Technology Research and Development Program of China(2015AA033803).

Service stress optimization of injection-molded engineering plastic product

WANG Xinyu1, LI Zheng1, GU Junfeng1, RUAN Shilun1,2, SHEN Changyu1,2, WANG Xicheng1,2

(1Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024, Liaoning, China;2State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, Liaoning, China)

Abstract:Recently, engineering polymer material is applied widely in aerospace and automotive fields. Engineering plastic products manufactured by injection molding have to endure mechanical, thermal and other complicated service conditions when they work. Under the complicated load conditions, the magnitude of service stress in engineering plastic parts is associated with the structure safety of the engineering devices, especially with people’s lives. Taking warpage and residual stress of a hemisphere polycarbonate product as the initial conditions of the mechanical analysis, this paper proposes an efficient service stress optimization strategy with respect to the process parameters and the structure of the product and cooling channel, which integrals injection molding analysis and mechanical analysis. The maximum service stress is finally reduced by using an optimization strategy based on Kriging surrogate model and EI method. The results indicate that the thickness of the product, melt temperature and packing pressure are critical factors to influence the service stress.

Key words:polymer processing; service stress; Kriging model; optimal design; product design