工业级错流列管式固定床反应器的CFD模拟
2016-08-06葛世轶黄正梁孙婧元王靖岱廖祖维蒋斌波阳永荣浙江大学化学工程与生物工程学院浙江杭州310027
杨 遥,葛世轶,黄正梁,孙婧元,王靖岱,廖祖维,蒋斌波,阳永荣(浙江大学化学工程与生物工程学院,浙江 杭州 310027)
工业级错流列管式固定床反应器的CFD模拟
杨遥,葛世轶,黄正梁,孙婧元,王靖岱,廖祖维,蒋斌波,阳永荣
(浙江大学化学工程与生物工程学院,浙江 杭州 310027)
摘要:工业级大型列管式固定床反应器壳程温度场与流场的均匀程度与反应的转化率及选择性密切相关。通过添加阻力源项和分散热源项,对工业级全尺寸错流列管式固定床壳程流场及温度场进行了CFD模拟研究,并进一步考察了折流板窗口区大小及其位置对壳程压降与温度分布的影响。结果表明,模拟得到壳程压降与由经验公式计算得到的压降较为接近,且壳程温度分布与工业实际数据吻合;增大窗口区面积,壳程压降呈现指数下降,同时高温差区(径向温差大于2 K)的范围与径向温差变大;随着第1块折流板位置降低,高温差区范围及径向温差均减小,但压降并不呈现规律性变化。模拟方法可用于工业级大型列管式固定床反应器的优化及设计。
关键词:固定床反应器;计算流体力学;优化
引 言
列管式固定床反应器由于其传热面积大,传热能量强,被广泛应用于正丁烷氧化制顺酐[1]、邻二甲苯制苯酐[2]及环氧乙烷制备[3]等强放热反应中。列管式固定床反应器与列管式换热器具有较为相似的结构特性,因此在列管式固定床设计过程中,设计者通常采用与换热器相同的设计标准,这一方法在反应器直径较小时,常可获得较好的设计结果;然而,随着反应器直径的增加,采用这一方法设计获得的反应器,其壳程换热介质的流动及传热均匀性逐渐变差,最终有可能使得反应器径向热点温差大于2 K[4],使得反应器的转化率及选择性下降。因此,对工业级大型列管式固定床反应器的壳程流场及温度场进行研究具有应用价值。
目前,模拟计算是研究列管式固定床反应器及换热器壳程流场与温度场的主要方法。这些方法可根据计算模型的不同分为3类。其一是基于多孔介质的流动模型,这类模型基于体积多孔度和分布阻力的概念,将管束分布的区域等效为各向异性的多孔介质[5-6];基于此类模型,研究者对 TEMA-E换热器[7-8]、带翅片管束管壳式换热器[9]、板翅式换热器[10]及固定床反应器[11-12]等的壳程管间流动场进行了模拟研究。第二类是流体流动分析模型,这一模型从壳程流体流动的特性入手,根据其流动途径不同细分为若干流股,通过对具有不同特性的流股单独建立流动方程,可对壳程流体的流场进行模拟研究[13-14]。近年来,随着商用仿真计算软件的快速发展,部分研究者开始着眼于通过CFD仿真模拟对列管式固定床及反应器壳程的流场及温度场进行研究。基于此方法,王定标等[15]对不同结构参数下大型纵流换热器的流动及传热进行了模拟研究;曹晓丽等[16]对并流反应器管间流体流动进行了研究;张敏华等[17]对直径3.5 m的列管式固定床反应器的部分(1/24)管束间单相流动与传热进行了研究;Kim 等[18]耦合管内管外传热对仅有200根反应管的列管式固定床反应器进行了优化设计。
上述3类方法已被研究者们广泛使用,然而这3类方法仍存在着一些问题。第1类与第2类方法均较难提供可视化流场及温度场,且第2类方法通常只能用于模拟构型简单的换热器及反应器;第 3类方法虽然可直接提供可视化的流场及温度场,但是直接模拟真实反应器,将会因其体积庞大、构型复杂等因素致使计算效率低下,使得研究者通常只能对小型实验室级反应器或者大型反应器的一部分进行研究,且难以包含传热过程。本文将第1类方法中所述的多孔介质的思想引入第3类方法用于简化计算提高计算效率,并通过数学分析在能量守恒方程中添加分散热源引入传热过程,对用于正丁烷氧化制顺酐的工业级大型全尺寸错流列管式固定床反应器壳程的流场及温度场进行了CFD模拟研究,并基于此方法对分布板窗口区尺寸及排布进行了优化。

图1 模拟对象的几何结构Fig. 1 Geometry structure of simulated domain
1 模拟对象
本文的模拟对象为某厂20000 t·a-1正丁烷氧化制顺酐的工业级列管式固定床反应器,如图1所示。为了在反应器壳间形成错流流场,该反应器壳程中距反应器壳体下端面1000、2500、4500 mm处分别装有3块盘环形折流板;其中两块环板的窗口区直径均为反应器内径的30%,即1500 mm;盘板直径为3500 mm。该反应器的其他结构参数见表1。

表1 模拟对象的结构参数Table 1 Parameters of simulated domain
工业运行过程中,反应器壳程换热介质为二元硝酸熔盐,由55%的硝酸钾和45%的亚硝酸钠组成,其密度为1800 kg·m-3,黏度为1.835 mPa·s,比热容为1867 J·kg-1·K-1,热导率为330 W·m-2·K-1。在工业装置中,进出口采用环状分布器以达到周向各进出口熔盐质量流量相等的目的,在模拟中将其简化为在周向上均匀分布的、直径均为600 mm的6个圆柱形进出口,见图2。进口管长250 mm,为了防止计算时出口发生回流,出口管略长于进口管,为 700 mm。模拟计算时,根据工业操作条件可计算得到每个入口的熔盐流速为1.57 m·s-1。

图2 熔盐进口分布Fig. 2 Layout of molten slat inlets
2 数学模型
为了简化计算提高计算效率,本文基于多孔介质的思想,通过添加阻力源项来模拟反应管对流场的影响,同时采用添加分散热源的方式来模拟反应放热对温度场的影响。
2.1 控制方程
本文假设壳程流体熔盐在操作条件下为不可压缩的牛顿流体,同时忽略换热过程中的辐射传热,可以得到在笛卡儿坐标系下的连续性方程、动量方程及能量方程,见式(1)~式(3),式中速度 u均为表观速度。
连续性方程

动量守恒方程能量守恒方程
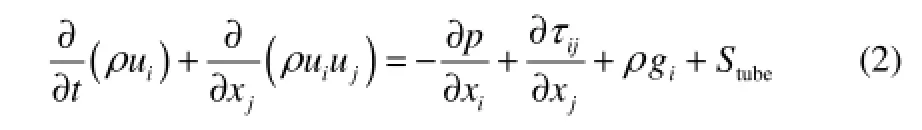
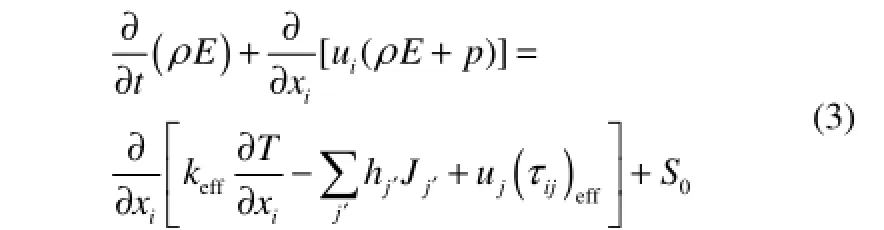
2.2 阻力源项
本文基于多孔介质的思想通过添加阻力源项来模拟管束对熔盐的流动阻力,即在描述动量传递的方程右侧添加一项由于管束存在导致的阻力源项,如式(2)右侧最后一项Stube所示,Stube可表达成式(4)的形式。

式中,Ci为流体流经不同方向的阻力系数,由管束的排布方式及流动方向决定,当流体错流流过管束时,阻力系数如式(5)所示,当流体顺流流过管束时,阻力系数如式(6)所示[19]。

式中,S为管心距,m;do为反应管外径,m;χ为管间距与反应管外径的比值;fi为不同方向的透过率,由管束排布的密度决定;Re为基于流体流经管束的最大速度和管外径的壳程Reynolds数。
2.3 换热源项
为了计算壳程流体的温度场,本文采用了添加分散热源的方式,将反应管与熔盐之间的换热量分散到每一个计算单元,在原有能量方程中添加了计算单位体积、单位时间内的换热量的源项S0,即式(3)右边的最后一项。
对于熔盐从周向等质量流量流入的盘环形列管式反应器,其换热单元应该为一个环形薄层,如图3所示。为了计算换热源项S0,假设此环形换热单元的高为 dz、厚度为 dr,该换热单元内共有 nr根反应管,每根反应管反应程度相同,管程温度相等,均为T;换热单元内熔盐温度为Tc;从周向各位置流入换热单元的熔盐总质量流量为Qin,温度为Tc1;流出换热单元的熔盐总质量流量为Qout,温度为Tc2;稳定状态下,流入与流出换热单元的熔盐质量流量相等,即Qin=Qout=Q。

图3 环形换热单元Fig. 3 Schematic diagram of annular heat transfer unit
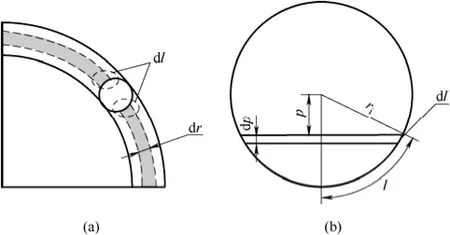
图4 换热面积Fig. 4 Schematic diagram of heat transfer area
据此,对单位时间内换热单元中的能量传递进行衡算可得到式(7)
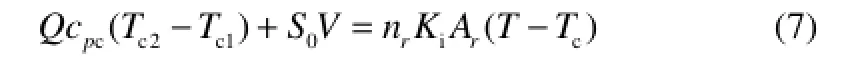
考虑到式(7)所描述的对象为非常薄的环形换热单元,且在工业操作过程中,多数反应器的径向温差一般不大于 2 K,因此在单位时间内流入与流出换热单元的熔盐温度差极小,即式(7)左边第1项约为0,由此可将式(7)进一步简化为式(8)

式(8)中V为薄层内熔盐体积,由于本文模拟中采用多孔介质模拟管束阻力,但是流动时的流通体积并没有变,因此 V=2πrdrdz,在笛卡儿坐标系下,;nr为换热单元内的列管数,是换热单元位置r的函数,且为不连续整数函数。
Ar为换热单元内单管的换热面积,为了计算Ar必须准确计算夹在换热单元的圆环截面内反应管的弧长dl[图4(a)],Ar=2dldz。进一步,如图4(b)所示,由几何条件可以得到如下关系

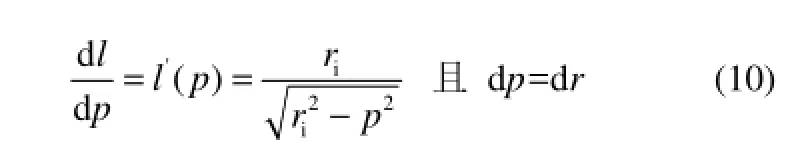
由式(9)及式(10)计算可以得到

将式(11)代入式(8)并进一步化简可得到单位时间、单位体积的换热热源S0如式(12)所示。

式中,Ki是基于反应管内径di的总传热系数,其计算式见式(13)。

式中,λt为管壁热导率,hw与α分别为管程与壳程对流传热系数,经计算发现管程传热热阻约是壳程传热热阻的200倍以上,因此在本文中忽略壳程传热热阻。式(12)中T为反应管管程温度,是轴向位置z的函数,可由工业数据拟合得到。拟合结果见图5及式(14)。


图5 管程温度随管长的变化Fig. 5 Variation of tube side temperature with tube length
3 模型求解
本文采用Fluent 6.3.26求解模拟对象的壳程流场及温度场。根据表1所示的换热管数及布管方式可计算得到反应器中布管区的范围,见图 6。在计算过程中,将整个计算主体分为内外两个区域,内区为布管区,在布管区采用 UDF添加阻力源项及分散热源项;外区为非布管区,不添加阻力源项及热源项。
计算过程中不考虑折流板与反应管间隙的漏流。计算主体网格由Gambit生成。分别采用0.2、0.5、1作为步长生成正六面体网格进行网格无差异检验,检验结果见图7。由图7可知,当步长小于0.5,网格尺寸将不会对模拟得到的壳程压降产生明显影响,因此采用0.5作为步长生成正六面体网格是合适的,采用此步长获得的网格总数约为240万个。计算采用三维、双精度、基于压力的稳态隐式求解器;进口边界条件设置为速度边界条件,出口边界条件设置为outflow,壁面选择标准壁面函数,湍流模型选择标准k-ε模型。收敛条件除能量方程为10-6之外,均为10-4。

图6 布管区Fig. 6 Schematic diagram of area with tubes

图7 网格无关性检验Fig. 7 Pressure drop at three different kinds of mesh
4 模型验证
4.1 壳程总压降
为了验证模拟结果的准确性,本文首先模拟了6种不同进口流速下熔盐流经此反应器的总压降,并将模拟结果与由经验公式计算得到的理论结果进行了对比。Stankiewicz[20]总结并分析了计算列管式固定床壳程压降的经验公式,根据其推荐,本文采用式(15)~式(19)来计算流体流经壳程的理论压降。
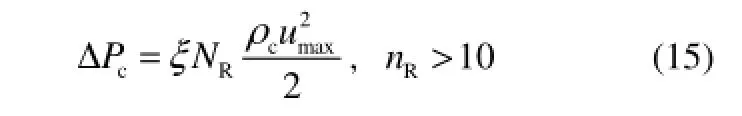

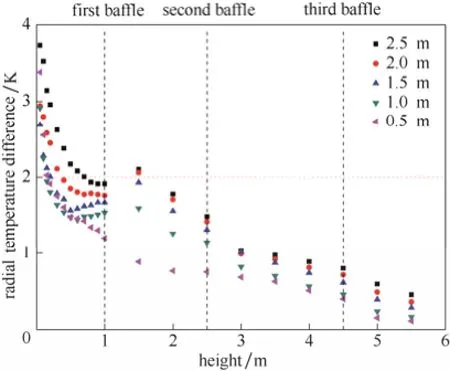
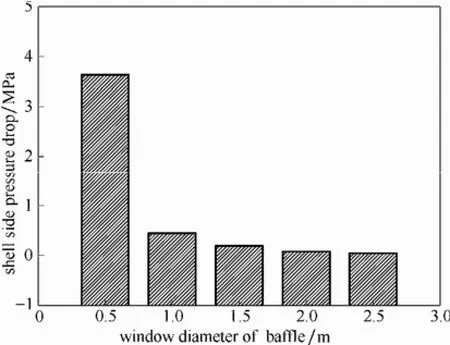
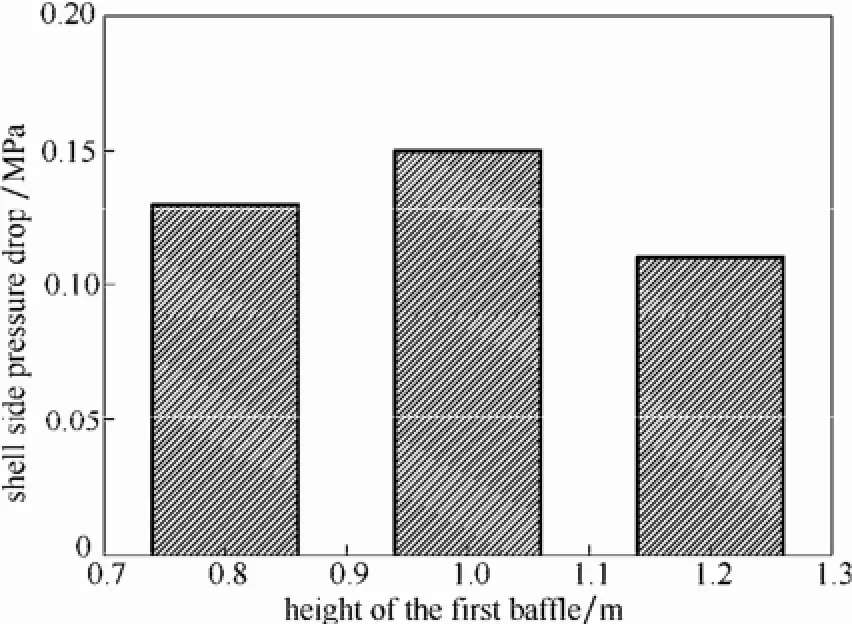
式中,ΔPc与ΔPw分别为流体流经管束和流过折流板窗口区的压降;NR为折流板重叠区管层数;umax为熔盐错流流经壳程时的最大流速,对于盘环形折流板,umax=Q/(πdwhfs),其中,dw为环板窗口区直径,h为两折流板之间的间距;Rec为基于反应管外径do和错流最大流速umax的Reynolds数,1≤Rec≤3×105;uw为窗口区流速,其适用范围为0.1 图8对比了模拟结果与经验计算结果。由图8可以看出,随着进口流速的增加,模拟值和经验值均呈现对数增长趋势;模拟值介于含窗口区压降的经验值与不含窗口区压降的经验值之间,且偏离含窗口区压降的经验值。在已有研究中,对于盘环形折流板窗口区压降的推荐经验公式较少,且这些经验公式的适用范围较小,因此由经验公式计算得到的理论窗口区压降值得商榷,这也导致模拟得到的壳程压降与由经验公式计算得到的理论压降存在一定误差。但是,总的说来,模拟值与理论值之间的相对误差总是小于15%,通过添加阻力源项的方法能够准确地模拟管束造成的流动阻力。 图8 模拟压降与经验压降的对比Fig. 8 Comparison between simulated pressure and pressure calculated by correlations 图9 双对数坐标系中模拟压降与进口气速的关系Fig.9 lnΔP vs lnUin 图9进一步将模拟得到的壳程压降与进口流速绘制于双对数坐标系中。由图可知,在双对数坐标系中,模拟压降与进口流速呈现直线关系,拟合可得到模拟压降与进口流速之间的关系如式(20)所示。 式(20)显示壳程压降与进口速度的1.79次方呈正比,这一结果与He等[21]的研究结果一致。He等研究发现,壳程湍流流动的压降与进口速度的指数关系为1.75~2.0。 4.2 壳程温度分布 本文进一步模拟了工业条件下床内壳程温度场分布,并将其与工业数据进行了对比,见图10。图中所述的工业数据为平稳运行过程中某一时刻各不同检测位置的熔盐温度,模拟数据为对应位置的模拟结果。由图可以看出,模拟得到的平均温度与工业检测得到的平均温度较为接近,但仔细对比模拟得到的结果与工业数据,也可发现一些不同。首先,工业数据中温度的波动要明显大于模拟结果;其次,在反应器底部,工业数据小于模拟结果,而除底部之外的大部分区域工业检测值大于模拟结果。这可能是由于工业数据来自于运行2年后的生产装置,经过长期的运行,反应器壳程出现了不均匀的结垢,这一方面加大了温度波动,另一方面也加大了熔盐流经反应器壳程的阻力损失,使得流速降低。如上所述,本文模拟的对象,其管程传热热阻是壳程传热热阻的200倍,传热主要由管程控制,因此结垢造成的流速降低并不会造成传热系数的较大变化,但是壳程流体流速的降低将会增加熔盐流经每一根管的停留时间从而加大熔盐流经每根换热管的换热量。因此相对于无结垢时的模拟结果,在工业反应器底部,从壳程向管程传递的热量增加, 使工业监测得到的温度低于模拟结果;而随着反应器高度的增加,当管程反应气体的温度高于壳程熔盐时,从管程向壳程传递的热量也增加,使工业监控得到的温度高于模拟结果。 图10 模拟得到的壳程温度与工业数据的对比Fig. 10 Comparison between simulated temperature in shell side and industrial data 经上述验证结果发现,采用本文所述的模拟方法可以较好地获得工业级列管式固定床反应器壳程整体压降及内部温度分布,因此可以采用此方法对列管式固定床反应器进行优化设计。本文将采用此方法,考察折流板窗口区面积及折流板位置对壳程压降及温度分布的影响。 5.1 折流板窗口区面积 折流板窗口区面积是影响错流列管式固定床壳程换热及流动特性的重要因素之一,其大小直接影响着壳程压降及壳程径向温差。图11给出了入口流速为1.31 m·s-1时,两块环板窗口区直径分别为0.5、1.0、1.5、2.0及2.5 m时,盘环形反应器纵向截面的温度分布。从图11可以看出,径向温差较大的区域主要出现在第1块折流板以下,且此处等温线呈现“山峰形”分布,峰顶位于第1块折流板的窗口区,峰宽及峰高随着窗口区面积的增大而增大。另外,壳程的热点区主要位于第2块折流板与第3块折流板之间,随着窗口区面积的增大先减小后增大,在窗口区直径为1.5 m时达到最小值。 为了进一步定量分析窗口区大小对径向温差的影响,本文计算了不同窗口区面积时反应器壳程熔盐径向温差沿轴向的分布,见图12。图12的结果表明,在本文考察的条件下,反应器壳程高温差(大于2 K)的区域均主要存在于第1块折流板以下;在同一轴向高度,反应器的壳程温差基本随窗口区面积的下降而下降;同时,除窗口区直径为0.5 m时,反应器壳程温差总是在某一窗口区面积下随着轴向位置的升高先减小再增大再减小,当窗口区直径为0.5 m时,这一变化规律有所改变,随着反应器轴向位置的升高,径向温差持续递减。 这一结果的产生是由于窗口区直径不同,则流体流经反应器壳程的压差不同,进而导致熔盐的流动型式不同。对于本文模拟的错流列管式,流体在壳间的流动主要由分布板重叠区的错流流动及窗口区的顺流流动组成,当窗口区直径不同时,这一错流及顺流的比例发生了变化,导致换热介质的流型及其流经壳程的压降不同,最终造成径向温差分布的差异。图13进一步给出了不同窗口区大小下反应器的壳程压降,可以发现随着窗口区的减小,反应器壳程的流场随之改变,壳程压差增大,且壳程压差的增长速度越来越大,当窗口区直径从1.0 m下降至0.5 m时,壳程压降急剧增加、发生突变。 图11 不同窗口区直径反应器的纵向截面温度分布Fig. 11 Temperature distribution of longitudinal cross-section of various reactors with different window sizes 图12 不同窗口区直径反应器的壳程径向温差Fig. 12 Radial temperature differences of various reactors with different window sizes 图13 不同窗口区直径反应器的壳程压降Fig. 13 Shell side pressure drops of various reactors with different window sizes 5.2 折流板位置 5.1节的研究结果表明,壳程径向温差较大的区域主要存在于第1块折流板以下,即高温差区(大于2 K)的大小直接受到第1块折流板位置的影响,因此有必要对第1块折流板的位置进行优化设计。图14为第1块折流板高度分别为0.8、1.0及1.2 m时纵向截面的温度分布。由图可知,随着折流板位置降低,反应器底部“山峰形”等温线的峰顶宽度逐渐增加,且当第1块折流板升高至1.2 m时,第2块折流板的上方出现了其他的热点区。为了进一步分析第1块折流板对径向温差的影响,本文计算了3种情况下反应器2.0 m以下区域的径向温差,见图15。图15显示,当折流板位于1.2 m处,反应器中1.6 m以下的区域径向温差均大于2 K;当折流板位于1.0 m处时,高温差区为低于0.4 m及1.2~1.4 m之间的区域;进一步降低折流板至0.8 m处,高温差区为低于0.2 m及1.0~1.2 m之间的区域,即降低第1块折流板确实能够使高温差区变小,但是随着折流板位置的降低,通过调节折流板位置从而减小高温差区的作用越来越不明显。 图14 不同折流板位置反应器的纵向截面温度分布Fig. 14 Temperature distribution of longitudinal cross-section of various reactors with the first baffle at different heights 图15 不同折流板位置反应器的壳程径向温差Fig. 15 Radial temperature differences of various reactors with the first baffle at different heights 图16为第1块折流板高度分别为0.8、1.0及1.2 m时反应器的壳程压降,结果显示改变第1块折流板的高度对壳程整体压降的影响不大。这是因为,虽然降低第1块折流板的高度将会使得第一块折流板以下的区域流速变大,从而压降变大,但是与此同时这也增大了第1块折流板与第2块折流板之间的流动通道,使得这一区域的流通阻力变小,因此在这双重作用下,改变第1块折流板的高度,壳程总压降并不呈现出规律性的变化。 图16 不同折流板位置反应器的壳程压降Fig. 16 Shell side pressure drops of various reactors with the first baffle at different heights 本文采用添加阻力源项模拟流体流经管束的压降,采用添加分散热源项的方式模拟管束换热,对年产20000 t·a-1正丁烷氧化制顺酐的工业级反应器的壳程压降及温度分布进行了模拟研究,得到了以下结论。 (1)本文采用的多孔介质模型和添加分散热源的方式能够较好地用于工业级尺寸列管式固定床反应器的模拟研究,模拟得到的压降与理论公式计算结果一致,获得的温度分布也与工业检测的结果基本一致。 (2)通过改变盘环形折流板的窗口区面积,可以达到有效改善流体流经壳程的压降及壳程的温度场;增大窗口区面积,壳程压降逐渐降低且降低幅度逐渐减小,同时高温差区的范围变大,径向温差变大。 (3)改变第1块折流板的位置可以达到改善壳程温度场分布的作用,随着第1块折流板位置降低,高温差区变小,径向温差减小;但是随着折流板位置降低,这一作用越来越不明显。另外,改变第 1块折流板的位置,其壳程压降并没有一致性规律。 综上,本文提出的模拟方法可用于工业级错流列管式固定床的设计及优化。同时,在错流列管式固定床设计过程中,为了尽可能地减少高温差区,使得径向温度分布更为均匀,可以在一定程度上降低第1块折流板的高度,同时减小折流板窗口区面积。然而,值得注意的是,窗口区面积及第1块折流板的高度也并非越小越好,而必须综合考虑这些因素对壳程温度场及壳程压力的影响,最终才可获得最优化设计。 符 号 说 明 Ar——单管在换热单元内的换热面积,m2 C ——多孔介质阻力系数,m-1 cp——比热容,J·kg-1·K-1 di,do——分别为管内、外径,m dw——折流板窗口区直径,m E ——能量,J g ——重力加速度,m·s-2 h ——折流板间距,m hw——壳程对流传热系数,W·m-2·K-1 ——总传热系数,W·m-2·K-1 NR——折流板重叠区管数 nr——换热单元内管数 Pc——错流压降,Pa Pw——窗口区压降,Pa p ——静压,Pa Q ——质量流率,kg·s-1 Stube,S0——分别为阻力源项、分散热源项 T ——温度,K t ——时间,s Uin——反应器进口流速,m·s-1 u ——速度,m·s-1 umax——错流流经管束的最大流速,m·s-1 uw——窗口区流速,m·s-1 V ——体积,m3 x ——位移,m α——管程对流传热系数,W·m-2·K-1 λt——管壁热导率,W·m-2·K-1 ξ ——阻力系数 ρ ——密度,kg·m-3 τ ——应力张量 References [1] SHARMA R K, CRESSWELL D L, NEWSON E J. Kinetics and fixed-bed reactor modeling of butane oxidation to maleic anhydride[J]. AIChE Journal, 1991, 37(1): 39-47. [2] CHOU Y S, WU C H. Passivity-based control of the phthalic anhydride fixed-bed reactor[J]. Chemical Engineering Science, 2007, 62(5): 1282-1297. [3] ZHOU X G, YUAN W K. Optimization of the fixed-bed reactor for ethylene epoxidation[J]. Chemical Engineering and Processing: Process Intensification, 2005, 44(10): 1098-1107. [4] 曹晓丽. 列管式固定床反应器管间流体流动特性的研究[D]. 上海:华东理工大学, 2008. CAO X L. Flow characteristics in a multi-tubular fixed-bed reactor[D]. Shanghai: East China University of Science and Technology, 2008. [5] SHA W T, YANG C I, KAO T T, et al. Multidimensional numerical modeling of heat exchangers[J]. Journal of Heat Transfer, 1982, 104(3): 417-425. [6] PRITHIVIRAJ M, ANDREWS M J. Three-dimensional numerical simulation of shell-and-tube heat exchangers(Ⅱ): Heat transfer[J]. Numerical Heat Transfer, Part A: Applications, 1998, 33(8): 817-828. [7] 邓斌, 陶文铨. 管壳式换热器壳侧湍流流动的数值模拟及实验研究[J]. 西安交通大学学报, 2003, 37(9): 889-893. DENG B, TAO W Q. Numerical simulation and experimental study on turbulent flow in shell side of shell-and-tube heat exchangers[J]. Journal of Xi’an Jiaotong University, 2003, 37(9): 889-893. [8] 邓斌, 陶文铨. 管壳式换热器壳侧湍流流动与换热的三维数值模拟[J]. 化工学报, 2004, 55(7): 1053-1059. DENG B, TAO W Q. Three-dimensional numerical simulation of turbulent flow and heat transfer characteristics in shell side of shell-and-tube heat exchangers[J]. Journal of Chemical Industry and Engineering(China), 2004, 55(7): 1053-1059. [9] 李欣, 邓斌, 陶文铨. 翅片管束式管壳式换热器三维数值模拟研究[J]. 工程热物理学报, 2005, 26(2): 316-318. LI X, DENG B, TAO W Q. Study on three-dimensional numerical simulation of shell-and-tube heat exchangers with finned rod bundles[J]. Journal of Engineering Thermophysics, 2005, 26(2): 316-318. [10] 彭波涛, 罗来勤, 王秋旺, 等. 多股流板翅式换热器的微分与优化数值研究[J]. 化工学报, 2004, 55(6): 876-881. PENG B T, LUO L Q, WANG Q W, et al. Numerical study of differential and optimal design for multi-stream plate-fin heat exchanger[J]. Journal of Chemical Industry and Engineering(China), 2004, 55(6): 876-881. [11] STANKIEWICZ A, EIGENBERGER G G. Dynamic modelling of multitubular catalytic reactors[J]. Chemical Engineering & Technology, 1991, 14(6): 414-420. [12] 刘永兵, 陈纪忠, 阳永荣. 固定床反应器中错流流动的数值模拟[J]. 高校化学工程学报, 2006, 20(4): 527-532. LIU Y B, CHEN J Z, YANG Y R. Numerical simulation of cross flow in fixed bed reactor[J]. Journal of Chemical Engineering of Chinese Universities, 2006, 20(4): 527-532. [13] TINKER T. Shell side characteristics of shell and tube heat exchangers[J]. General Discussion on Heat Transfer, 1951: 89-116. [14] KAKAC S. Heat Exchangers: Thermal-hydraulic Fundamentals and Design[M]. Misc-Sci/Eng, 1981. [15] 王定标, 向飒, 董其伍, 等. 纵流壳程换热器的三维流场[J]. 化工学报, 2004, 55(5): 699-703. WANG D B, XIANG S, DONG Q W, et al. Flow field in heat exchanger with longitudinal flow of shell-side[J]. Journal of Chemical Industry and Engineering(China) , 2004, 55(5): 699-703. [16] 曹晓丽, 沈荣春, 束忠明, 等. 平行流列管式固定床反应器管外流动的数值模拟[J]. 化学反应工程与工艺, 2008, 24(4): 301-304. CAO X L, SHEN R C, SHU Z M, et al. Simulation of fluid flow in shell side of parallel multitubular reactor[J].Chemical Reaction Engineering and Technology, 2008, 24(4): 301-304. [17] 张敏华, 百璐, 耿中峰, 等. 列管式固定床反应器管束间单相流动与传热的CFD研究[J]. 高校化学工程学报, 2013, 27(2): 222-227. ZHANG M H, BAI L, GENG Z F, et al. CFD simulation of fluid flow and heat transfer of single phase inside the shell side of multitubular fixed bed reactor[J]. Journal of Chemical Engineering of Chinese Universities, 2013, 27(2): 222-227. [18] KIM W, YUN C, JUNG K T, et al. Computer-aided scale-up of a packed-bed tubular reactor[J]. Computers & Chemical Engineering, 2012, 39: 96-104. [19] YOU Y, FAN A, HUANG S, et al. Numerical modeling and experimental validation of heat transfer and flow resistance on the shell side of a shell-and-tube heat exchanger with flower baffles[J]. International Journal of Heat and Mass Transfer, 2012, 55(25): 7561-7569. [20] STANKIEWICZ A. Advances in modelling and design of multi-tubular fixed-bed reactors[J]. Chemical Engineering & Technology, 1989, 12(1): 113-130. [21] HE Y, TAO W Q, DENG B, et al. Numerical simulation and experimental study of flow and heat transfer characteristics of shell side fluid in shell-and-tube heat exchangers[C]//Proceedings of Fifth International Conference on Enhanced, Compact and Ultra-Compact Heat Exchangers: Science, Engineering and Technology. Hoboken, NJ, USA, 2005: 29-42. 2016-01-11收到初稿,2016-04-18收到修改稿。 联系人:黄正梁。第一作者:杨遥(1989—),男,博士研究生。 Received date: 2016-01-11. 中图分类号:TQ 062.1 文献标志码:A 文章编号:0438—1157(2016)07—2692—10 DOI:10.11949/j.issn.0438-1157.20160047 基金项目:国家自然科学基金项目(91434205);国家杰出青年科学基金项目(21525627);浙江省杰出青年科学基金项目(LR14B060001);高等学校博士学科点专项科研基金(20130101110063)。 Corresponding author:HUANG Zhengliang, huangzhengl@zju.edu.cn supported by the National Natural Science Foundation of China (91434205), the National Science Fund for Distinguished Young (21525627), the Natural Science Foundation of Zhejiang Province (LR14B060001) and the Specialized Research Fund for the Doctoral Program of Higher Education of China (20130101110063). CFD simulation of cross flow in multi-tubular fixed-bed reactor of industrial level YANG Yao, GE Shiyi, HUANG Zhengliang, SUN Jingyuan, WANG Jingdai, LIAO Zuwei, JIANG Binbo, YANG Yongrong Abstract:The conversion and selectivity of an extremely large multi-tubular fixed-bed reactor of industrial level remarkably relate to the distribution homogeneity of temperature and flow of heat transfer medium in shell side. In this work, through introducing two items of resistance source and a dispersed heat transfer source, the distribution of temperature and flow in the shell of a multi-tubular fixed-bed reactor of industrial level for butane oxidation to maleic anhydride was investigated by CFD simulation. Subsequently, effects of the window size and the location of baffles on the pressure drop of shell side and the distribution of temperature and flow were studied. It showed that the pressure drop of the shell side achieved by simulation are in good agreement with that by calculation of experimental equations, and the simulated temperature distribution of shell side is in accordance with industrial experimental data. With an increase in window area of the baffles, the pressure drop of shell side exponentially decreased, the range of large temperature difference (with a radial temperature difference greater than 2 K), and the radial temperature difference increased. With a decrease in height of the first baffle, both the range of large temperature difference and the radial temperature difference reduced, while the pressure drop of shell side did not show any consistent changes. Here the modeling strategy can be a good way to optimize the design of extremely large multi-tubular fixed-bed reactor of industrial level. Key words:fixed-bed reactor; CFD simulation; optimal design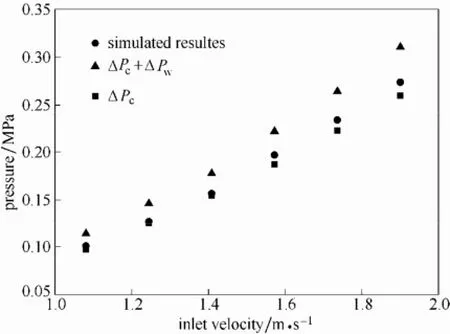

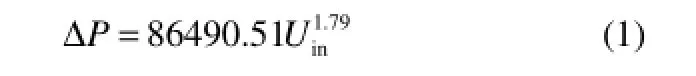

5 不同反应器型式的考察



6 结 论
(College of Chemical and Biological Engineering, Zhejiang University, Hangzhou 310027, Zhejiang, China)
