基于ELM的一类不确定性纯反馈非线性系统的Backstepping自适应控制

李　军，石　青



基于ELM的一类不确定性纯反馈非线性系统的Backstepping自适应控制

李军，石青

（兰州交通大学自动化与电气工程学院，甘肃 兰州 730070）

摘要:针对一类不确定性纯反馈非线性动力学系统，在中值定理、Backstepping控制的基础上，提出一种基于极限学习机(ELM)的自适应神经控制方法。ELM随机确定单隐层前馈网络(SLFNs)的隐含层参数，仅需调整网络的输出权值，能以极快的学习速度获得良好的推广性。在每一步的Backstepping设计中，应用ELM网络对子系统的未知非线性项进行在线逼近，通过Lyapunov稳定性分析设计的权值参数自适应调节律，可以保证闭环非线性系统所有信号半全局最终一致有界，系统的输出收敛于期望轨迹的很小邻域内。将所设计的控制方法应用于化工过程中的连续搅拌反应釜(CSTR)非线性系统实例中，仿真结果表明了控制方法的有效性。

关键词:非线性动力学；自适应；控制；Backstepping；极限学习机；神经网络

引 言

Backstepping控制方法[1-2]也称为反演控制，它目前已成为一大类非线性动力学系统的主流设计方法，与反馈线性化控制技术相比，它能灵活地避免系统中有用的非线性项被抵消，且很容易地保证系统的全局稳定性。它在每一步的设计中，将复杂的非线性动力学系统分解为不超过系统阶次的子系统，然后为每个子系统分别设计Lyapunov函数及中间虚拟控制量，一直“后退”到整个系统，直到完成整个控制律的设计。自适应神经控制[3-5]或自适应模糊控制[6-7]在应对非线性的参数变化、未建模动态以及外界干扰等方面具有更加优越的性能，尤其是结合 Backstepping设计的自适应控制方法[8-12]在非线性系统的控制中已得到广泛的应用，它解决了一大类非线性动力学系统的全局稳定性以及渐进跟踪性等问题。

文献[8-10]在自适应 Backstepping设计的基础上，提出了不同的神经网络自适应 Backstepping控制方法，且取得了较好的控制效果，它们均是针对如式(1)所示的严格参数反馈非线性系统进行的，即

与严格反馈非线性动力学系统相比，化学反应、飞行控制、生化过程等纯反馈非线性动力学系统是一类更一般的且更能真实描述的非线性系统[11]。纯反馈形式的非线性系统与严格反馈非线性系统一样，均具有三角形结构，且状态变量仅依赖于[x1,x2,…,xi+1]T，i=1,…,n-1。区别在于严格反馈非线性系统是一类特殊形式的纯反馈非线性系统，系统具有仿射形式的结构，即每个状态变量以及控制输入是仿射的，而纯反馈非线性系统往往具有非仿射形式的结构。实际应用中的大多数工程系统本质上是非仿射的，因此研究纯反馈非线性系统具有更好的工程实用价值。文献[12]针对一类非仿射的纯反馈单输入单输出非线性系统，提出了一种自适应变结构神经网络控制策略, 而且证明闭环系统的所有信号在平衡点上是半全局一致有界的。文献[13]提出一种基于RBF神经网络的Backstepping自适应控制方法，所设计的控制器能满足闭环系统的所有信号半全局一致最终有界，通过适当地选择设计参数，能保证闭环系统的控制性能。在上述文献中，由于前馈神经网络、RBF神经网络或模糊逻辑系统的良好逼近特性，且具有自适应学习的特点，可用于逼近非线性系统的不确定部分，进一步基于Lyapunov综合法设计参数的在线自适应调节律，以保证控制系统的闭环稳定性。但是在网络结构的确定方面，如径向基函数(radial basis function, RBF)神经网络的隐含层节点的参数或模糊系统的隶属度函数构造上，主要利用先验知识确定，有时会影响闭环系统的跟踪精度和控制效果，存在一定的不足。

极限学习机(extreme learning machine, ELM)是由Huang等[14-15]提出的用于单隐层前馈网络(single layer feedback networks, SLFNs)的快速学习算法，其特点是随机选择 SLFNs的隐含层节点及相应的节点参数，在训练过程中仅需调节网络的输出权值。针对单数单输出仿射非线性系统，文献[16]给出了基于 ELM的直接自适应神经控制方法，应用于倒立摆基准实例中。针对一类多输入多输出严格反馈非线性动力学系统，文献[17]给出了基于ELM的自适应Backstepping控制方法，应用于双轴运动平台实例中；文献[18]给出了基于ELM的鲁棒自适应控制方法，应用于二自由度刚性机械臂实例中，均取得了很好的控制效果。

鉴于ELM在参数选择和学习速度方面的优势，针对一类不确定性纯反馈非线性动力学系统，在Backstepping设计与中值定理的基础上，本文提出一种基于ELM的自适应神经控制方法，将其应用于化工过程中的连续搅拌釜(continuous stirred taank reactor, CSTR)系统的控制实例中，以验证本文方法的有效性。

1　问题描述

考虑如下一类不确定性纯反馈非线性系统

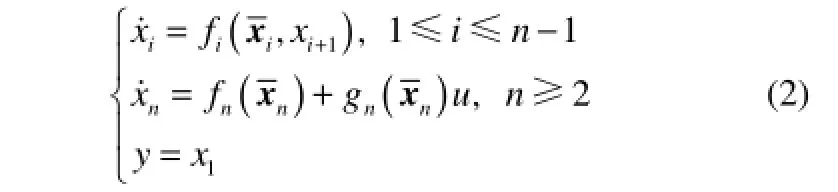
为将式(2)变形为严格反馈形式的非线性系统，首先，由中值定理在给定平衡点附近进行泰勒级数展开，即

其中，xi0是对应t0时刻的给定值，其次，将式(3)代入式(2)得

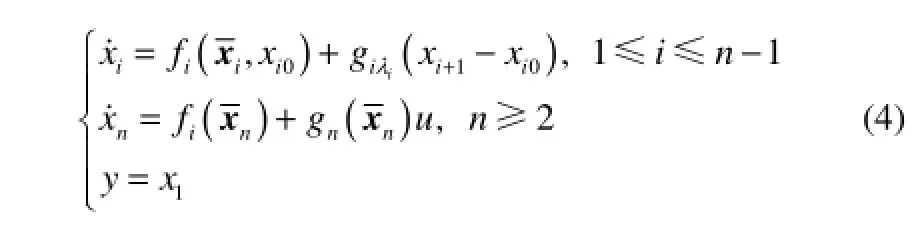
针对式(4)的严格参数反馈形式的非线性动力学系统方程，可以通过Backstepping控制思路，设计控制律 u(t)，以保证闭环系统的所有信号半全局一致最终有界，使得系统的输出能够跟踪给定的期望轨迹 yd(t)。非线性动力学系统式(4)满足如下假设。

假设1 期望轨迹yd有界，且存在n阶导数，其各阶导数均可微有界。

假设2 函数gi(·)是符号已知的光滑函数，并且存在常数，使得。

假设2表明光滑函数gi(·)严格为正或为负，不失一般性，可设

另外，由式(3)看出，gi(·)的偏微分仅依赖于状态变量，而fi(·)和gn(·)假定是光滑函数，在紧集合Ω内是有界的。因此，进一步给出假设3。

2　极限学习机

2.1 ELM

ELM起源于对SLFNs的研究，是SLFNs的推广和延伸，其本质不同于对SLFNs学习算法的通常理解，即其隐含层的节点及其参数均无须调整，与训练数据独立，随机的确定隐含层节点。

对于含有 L个隐含层节点，m个输出节点的SLFNs，其网络输出的数学描述为

式中，wi、bi表示网络隐含层节点的学习参数；θi表示连接第i个隐含层节点与网络输出层节点的输出权值向量；hi(x)表示第 i个隐含层节点的输出函数h(x;wi,bi)，h(x;wi,bi)由隐含层节点类型确定。

当隐含层节点为可加性Sigmoid激活函数时

当隐含层节点为RBF激活函数时

当隐含层节点为硬限幅Hard-limit激活函数时

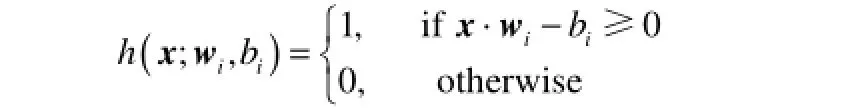
其中，wi∈Rn,bi∈R，wi·x表示向量wi和x的内积。

2.2 ELM的学习

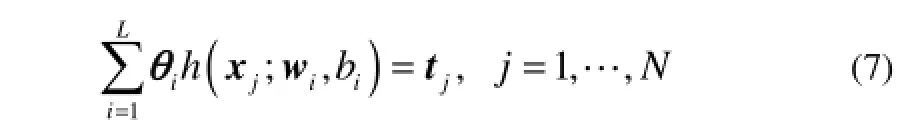
以矩阵形式表示为

其中

这里，H为SLFNs的隐含层输出矩阵，其第i行表示与输入xi相关的特征映射，即xi:h（xi），且h（x）=[h（x;w1,b1）,…,h（x;wL,bL）]。

若h(xj;wi,bi)在任意区间上无限可微，且SLFNs隐层节点及节点参数可以随机生成，则由文献[15]可知，当隐含层节点数目L小于样本N时，SLFNs仍能以极小的训练误差逼近训练样本。此时矩阵H并非方阵，从而存在使得

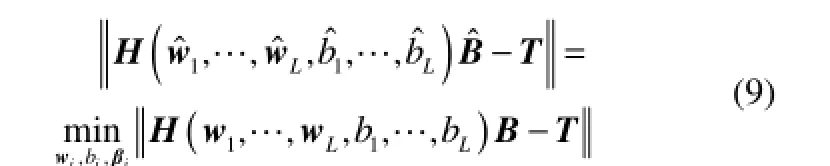
因此，与使用梯度下降算法训练所有网络权值的SLFNs方法不同，ELM的基本学习算法就是求解式(9)的权值最小二乘解。

2.3 ELM对未知非线性函数的逼近

实际的控制工程中，基于前馈神经网络的良好逼近特性，通常可应用RBF神经网络或SLFNs对未知非线性函数进行建模。本文将应用 ELM逼近未知连续函数 ϕ（Z）∈R，输入向量Z∈Rn。因此，式(8)中的B∈RL×m此时成为L×1的列向量，H∈RN×L成为列向量h（Z）∈R1×L，即有

假设4 对所有的Z∈ΩZ，存在最优输出权值向量，满足≤ε∗，常数ε∗＞0。

3　Backstepping自适应神经控制器的设计

Backstepping控制是一种逐步递推的设计方法，通过引进虚拟控制量达到静态补偿，前面的子系统必须通过后边子系统的虚拟控制达到镇定的目的。本节针对式(2)所示的一类不确定性纯反馈非线性系统，将其变换为式(4)后，应用ELM网络逼近子系统的未知部分，并使用Lyapunov综合方法保证系统的半全局一致最终稳定，设计出 Backstepping自适应控制器。

Step 1 定义跟踪误差e1=x1-yd，则其导数为

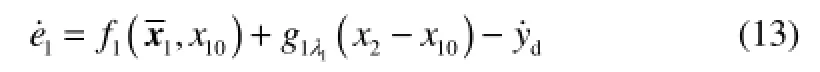
将x2视为虚拟控制输入，则存在一个期望反馈控制

其中，设计参数 b1＞0；f1和11gλ均是未知光滑函数。

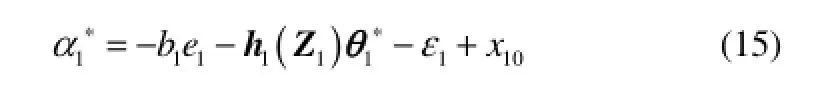
在国内，虽然一些酒店企业也拥有较丰富的管理经验，但是往往没有形成系统成熟的管理模式。在信息发达的今天，很多酒店没有很好地利用起这一优势，在信息化管理方面欠缺，设施不齐全。很多企业在借鉴其他企业经验或者从酒店管理公司获得管理技术时没有结合本企业的实际情况和发展特点。此外，我国酒店大多都是小规模经营，而且地区差异较大，发展不平衡，不能适应世界酒店发展的趋势，更没有吸取到世界上信息化管理酒店这一模式的好处，与全球较为成功的酒店还存在很大的差距。

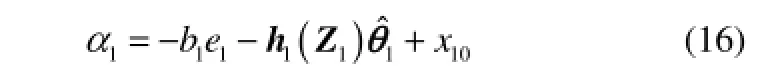
式(18)求导可得

设计权值 ˆiθ的自适应律为其中，γi>0，σi>0为设计参数。

令b1=b10+b11,b10,b11>0，考虑式(20)的自适应律在不同情形下的取值。

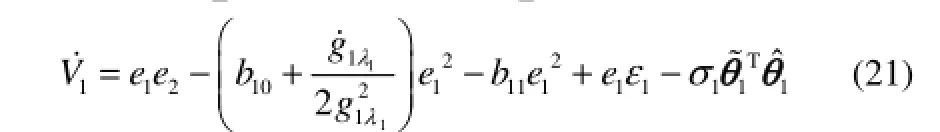
应用完全平方公式，有如下不等式成立

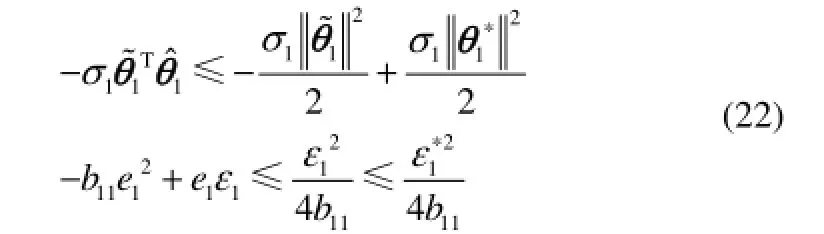
由假设2及假设3，可得

则有

可见，对于自适应律在不同情形下的取值，均能保证式(24)成立。

Step 2 定义e2=x2-α1，则其导数为

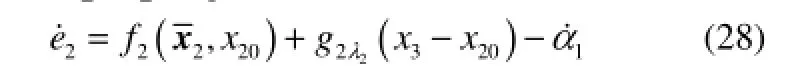
将x3视为虚拟控制输入，存在一个期望反馈控制

其中，b2>0是一个设计参数。由式(14)可知，α1是关于x1、yd和的函数，则

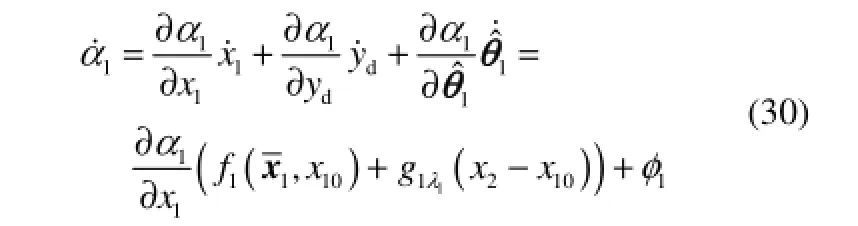
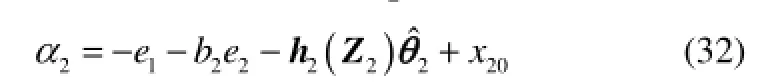
选择Lyapunov函数为

式(34)求导可得

应用完全平方公式，有如下不等式成立

另外，由假设2及假设3，可得

由式(35)得

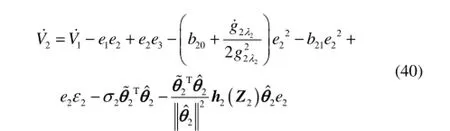
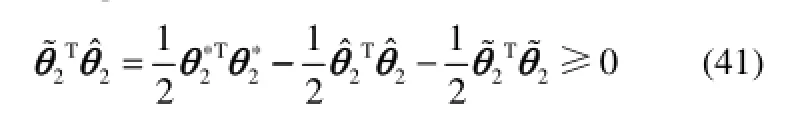
因此，无论自适应律为何种形式，均能保证式(39)成立。Step定义，其导数为

将 xi+1视为虚拟控制输入，存在一个期望反馈控制

其中，bi>0是一个设计参数。是关于及的函数，因此，可有

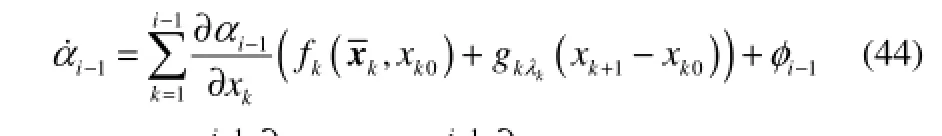
选择Lyapunov函数为

式(48)求导可得

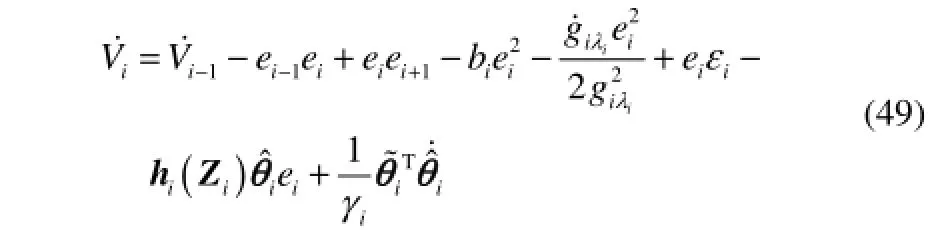
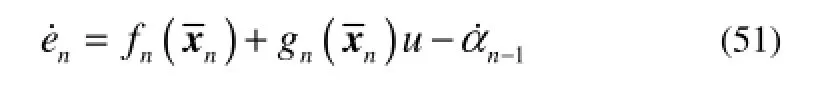
为了使整个系统稳定，存在一个期望反馈控制

其中，bn>0是一个设计参数。是关于及的函数，因此，可有

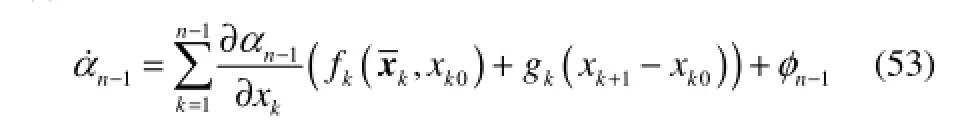
则

选择Lyapunov函数为

式(57)求导，结合权值 ˆnθ的自适应律，与Step i的推导类似，可得如下不等式

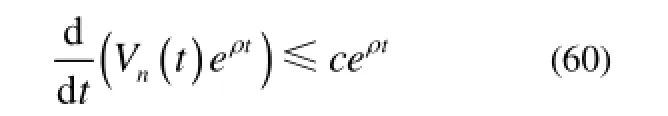
在[0,t]内，式(60)积分，可得

在控制器的每步反演设计过程中，由于待逼近的ϕi(Zi)依赖于上一步设计中的神经网络权值向量的影响，通过引入中间变量，则有效避免了第i步设计中，ELM网络的输入产生“维数灾难”的不利情形。因此，每步设计中，均可应用有限数目输入的 ELM网络逼近子系统的未知部分。

4　仿真研究

为了验证本文控制方法的有效性，以一阶连续搅拌反应釜(CSTR)系统的不可逆放热反应AB过程为例。该模型是一类典型的纯反馈非线性系统，其质量和能量平衡方程式[19-20]为

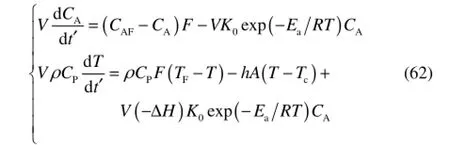
其中，CA为反应物A的浓度，T是反应釜温度，冷却剂温度Tc为操作控制变量。

与文献[21]的处理一致，首先引入以下量纲 1形式的参数，即

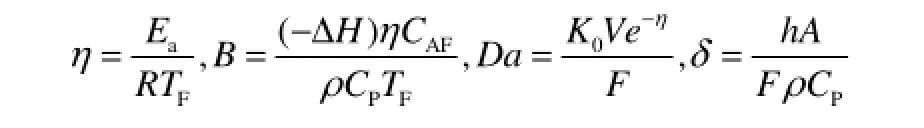
其中，F、CAF和TF分别是过程流量、进料浓度、进料温度。定义量纲1形式的变量如下

其中，TCO是冷却液温度的参考值。

在上述定义的基础上，对式(62)进行变换，可转换为量纲1的模型方程如下

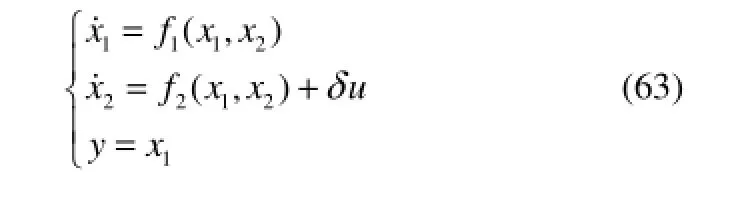
其中

x1和x2分别是量纲1反应浓度和温度，输入u是夹套内的冷却剂温度，Da是Damkohler数，η是量纲1活化能，B是反应热，δ是热交换系数。

可见，式(63)与式(2)的形式一致，本质上属于纯反馈非线性系统。选择参数 Da=0.072，η=20，B=8，δ=0.3。当u=0时，式(63)有3个平衡状态[7]x1=(0.1440,0.8862)，x2=(0.4472,2.7520)，x3=(0.7646,4.7052)=控制目标是通过设计控制律u希望反应器能够到达操作点（平衡状态）或者在操作点附近波动，即使系统的输出y=x1能够跟踪给定的期望轨迹yd，且保证闭环系统的所有信号均一致最终有界。

4.1 仿真一

选择系统的平衡状态x1=(0.1440,0.8862)，为获取光滑的参考信号，可使用线性参考模型将不连续的参考信号 r(t)变换为期望参考信号 yd。线性二阶的参考模型为

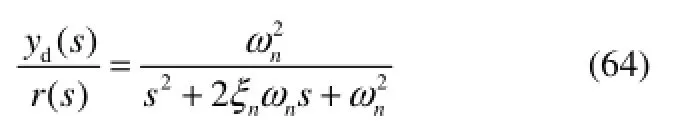
其中，r(t)是所选平衡状态0.1440附近±0.02的阶跃信号，ωn=5 r·min-1，ξn=1.0,yd(0)=0.1。初始条件x(0)=[0.1440,0.8862]T。

在设计参数的选取中，依据相关文献的经验取值及试凑法，通过多次实验仿真，即可选取一组较优的取值。设计参数为:σ1=σ2=2，γ1=0.002，γ2=0.2，b1=3600，b2=30，x10=0.1440。ELM 网络的隐含层节点分别考虑 Sigmoid可加性节点、RBF节点及Hardlim节点，网络及的隐含层节点分别为5和10，输入分别为3和4维，即，隐含层节点参数(w,b)分别在［-1,1］及[0,1]之间随机给定。用于对比的基于RBF网络的Backstepping自适应控制方法中，其隐含层节点个数也分别选取5和10，高斯基函数参数中心矢量值按均匀分布在网络输入值范围内的值选取，范围均为[-2,2]，基宽取值为0.1。

图1及图2分别给出了在权值自适应律式(20)调节下，基于控制律式(55)的条件下，量纲1反应浓度x1的跟踪曲线及跟踪误差曲线，可以看出采用不同节点的基于ELM的自适应Backstepping控制方法取得了很好的跟踪控制效果，也略微优于基于RBF的自适应控制方法。图3给出了控制输入的变化曲线。同时，为进一步从数值上比较差异，不同控制方法对状态变量 x1的跟踪输出与参考轨迹 yd之间的均方根误差(root mean square error, RMSE)也在表1列出。表1的结果显示，基于ELM的自适应Backstepping控制方法，其RMSE较小，这也验证了其良好的跟踪性能以及方法的有效性。

图1　x1的跟踪曲线Fig.1 Tracking curve of x1

图2　x1的跟踪误差曲线Fig.2 Tracking error curve of x1

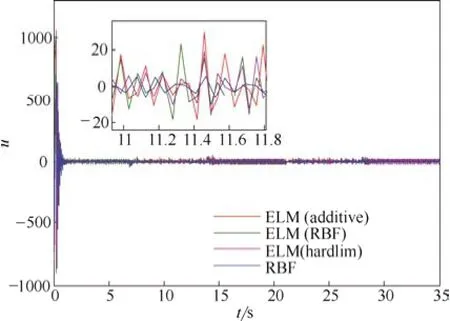
图3　控制输入uFig.3 Control input u

表1　不同控制方法的评价指标比较(仿真一)Table 1 Comparison of performance index of different control methods(simulation 1)

另外，实验还考虑了基于3种不同节点类型的ELM控制器，其隐含层节点数目变化时，所施加控制方法对控制性能的影响。当两个ELM网络的隐含层节点数目分别从5增加至25时，其状态变量x1跟踪参考轨迹yd的RMSE变化很微小，数值范围大约在0.0010～0.0013之间，这说明不同类型隐含层节点的ELM控制器，其控制性能相当，控制方法的鲁棒性好。

进一步考虑 ELM网络的隐含层节点参数的不同初始值设置对控制性能的影响，以Sigmoid节点为例，节点数目均为10，分别改变w和b取值的随机间隔范围，其中w的取值在[-0.5, 0.5]～[-4, 4]之间变化，b的取值在[0, 0.5]～[0, 4]之间变化时，状态变量x1跟踪参考轨迹yd的均方根误差(RMSE)变化很微小，控制器的性能几乎不受影响。

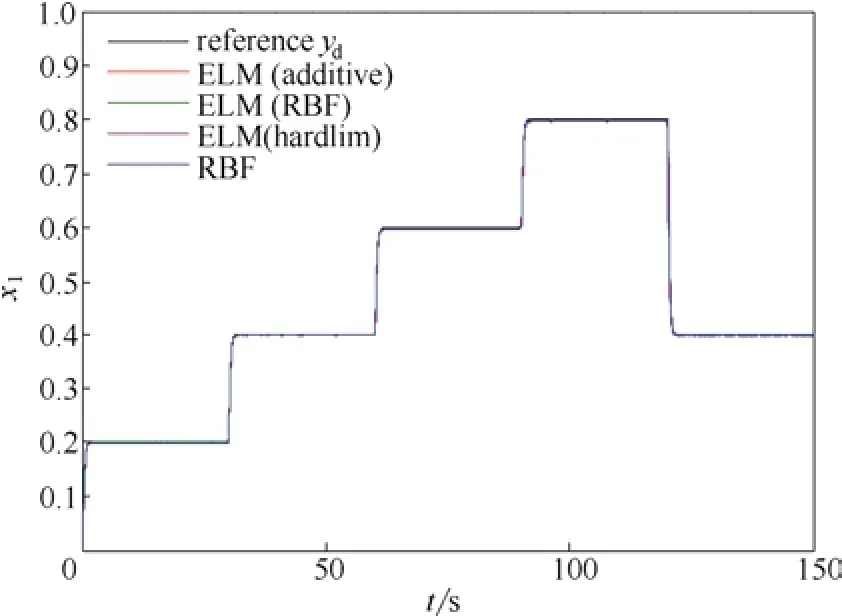
图4　x1在不同设定点的跟踪曲线Fig.4 Tracking curve of x1for different set-points

4.2 仿真二

与文献[7]的仿真情形一致，考虑系统在不同设定点情形下，控制器对量纲1反应浓度x1的跟踪性能。ELM网络的隐含层节点类型同仿真一，网络及的隐含层节点数目均为10，，隐含层节点参数(w,b)分别在[-1,1]及[0,1]之间随机给定。初始条件 x(0)=[0,0]T。设计参数选取为σ1=σ2=2，γ1=0.0002，γ2=0.2，b1=1800，b2=60，x10=0。用于对比的基于RBF网络的Backstepping自适应控制方法中，其隐含层节点数目也均为10，高斯基函数参数中心矢量值的范围为[-2,2]，基宽的取值为0.1。

图4和图5分别给出了量纲1反应浓度x1在不同设定点的跟踪曲线和跟踪误差曲线，图6进一步给出了控制输入的变化曲线。从仿真结果可以看出，采用 Sigmoid可加性节点和 RBF型节点的基于ELM的Backstepping自适应控制方法，其控制性能相当，略优于采用Hardlim硬限幅节点的ELM控制方法。不同节点类型的ELM控制方法，与基于RBF网络的自适应控制方法相比，其控制效果更好。

图5　x1在不同设定点的跟踪误差曲线Fig.5 Tracking error curve of x1for different set-points

图6　控制输入uFig.6 Control input u

表3　不同控制方法的评价指标比较(仿真二)Table 2 Comparison of performance index of different control methods(simulation 2)

为体现数值差异，不同控制方法中，状态变量x1的跟踪输出与参考轨迹yd之间的RMSE也在表2列出。从表 2的结果看出，基于 ELM的自适应Backstepping控制方法，其RMSE较小，这也验证了其良好的跟踪性能及方法的有效性。

5　结 论

Backstepping控制在设计不确定性系统的自适应控制器或鲁棒控制器方面已显示出一定的优越性，本文针对一类不确定性纯反馈非线性系统，通过中值定理，将其变换为严格反馈非线性系统的形式，在此基础上，给出了基于ELM的Backstepping自适应神经控制方法。该方法基于Backstepping控制设计步骤，应用 ELM网络逼近每一子系统的未知非线性项，由Lyapunov综合法设计参数自适应调节律，通过对 ELM网路输出权值的在线自适应调整，确保了闭环系统的所有信号半全局一致最终有界。最后，通过应用于化工过程的CSTR系统中，以其作为典型的纯反馈非线性系统实例，在不同的仿真情形下验证了本文控制方法的有效性。

References

[1] KANELLAKOPOULOS I, KOKOTOVIC P V, MORSE S. Systematic design of adaptive controllers for feedback linearizable systems[J]. IEEE Transactions on Automatic Control, 1991, 36(11): 1241-1253.

[2] KRASTIC M, KANELLAKOPOULOS I, KOKOTOVOC P. Nonlinear and adaptive Control Design[M]. HAYKLN S. New York, NY: John Wiley & Sons, 1995: 106-159.

[3] POLYCARPOU M M. Stable adaptive neural control scheme for nonlinear systems[J]. IEEE Transactions on Automatic Control, 1996, 41(3): 447-451.

[4] GE S S, HANG C C, ZHANG T. Nonlinear adaptive control using neural networks and its application to CSTR systems[J]. Journal of Process Control, 1999, 9(4): 313-323.

[5] 李冬娟. 连续搅拌反应釜的自适应神经网络控制[J]. 化工学报, 2013, 64(12): 4674-4680.

LI D J. Adaptive neural network control for continuous stirred tank reactor[J]. CIESC Journal, 2013, 64(12): 4674-4680.

[6] LABIOD S, GUERRA T M. Adaptive fuzzy control of a class of SISO nonaffine nonlinear systems[J]. Fuzzy Sets and Systems, 2007, 158(10): 1126-1137.

[7] CAO Y Y, FRANK P M. Analysis and synthesis of nonlinear time-delay systems via fuzzy control approach[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(2): 200-211.

[8] CHEN W, GE S S. Globally stable adaptive Backstepping neural network control for uncertain strict-feedback systems with tracking accuracy known a priori[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(9): 1842-1854.

[9] ZHANG T, GE S S, HANG C C. Adaptive neural network control for strict-feedback nonlinear systems using Backstepping design[J]. Automatica, 2000, 36(12): 1835-1846.

[10] GE S S, WANG C. Adaptive neural control of uncertain MIMO nonlinear systems[J]. IEEE Transactions on Neural Networks, 2004, 15(3): 674-692.

[11] 胡云安, 程春华, 邹强, 等. 非仿射纯反馈系统的间接自适应神经网络控制[J]. 控制理论与应用, 2014, 31(4): 467-478.

HU Y A, CHENG C H, ZOU Q, et al. Indirect adaptive neural networks controller for non-affine pure-feedback systems[J]. Control Theory & Application, 2014, 31(4): 467-478.

[12] 杜红彬, 李绍军. 一类纯反馈非仿射非线性系统的自适应神经网络变结构控制[J]. 系统工程与电子技术, 2008, 30(4): 723-726.

DU H B, LI S J. Adaptive neural network variable structure control for a class of non-affine nonlinear pure-feedback systems[J]. Journal of System Engineering and Electronics, 2008, 30(4): 723-726.

[13] GE S S, WANG C. Adaptive NN control of uncertain nonlinear pure-feedback systems[J]. Automatica, 2002, 38(4): 671-682.

[14] HUANG G B, CHEN L, SIEW C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes[J]. IEEE Transactions on Neural Networks, 2006, 17(4): 879-892.

[15] HUANG G B, WANG D H, LAN Y. Extreme learning machines: a survey[J]. International Journal of Machine Learning and Cybernetics, 2011, 2(2): 107-122.

[16] RONG H J, ZHAO G S. Direct adaptive neural control of nonlinear systems with extreme learning machine[J]. Neural Computing and Applications, 2013, 22(3): 577-586.

[17] 李军, 乃永强. 基于ELM的一类MIMO仿射非线性系统的鲁棒自适应控制[J]. 控制与决策, 2015, 30(9): 1559-1566.

LI J, NAI Y Q. Robust adaptive control for a class of MIMO affine nonlinear systems using extreme learning machine[J]. Control and Decision, 2015, 30(9): 1559-1566.

[18] ELKOTESHYA Y, JIAO L C, CHEN W S. ELM-based adaptive Backstepping neural control for a class of uncertain MIMO nonlinear systems with predefined tracking accuracy[J]. International Journal of Control, 2014, 87(5): 1047-1060.

[19] 朱群雄, 王军霞. 连续搅拌釜式反应器的鲁棒最优控制[J]. 化工学报, 2013, 64(11): 4114-4120.

ZHU Q X, WANG J X. Robust optimal control for nonlinear continuous stirred reactor[J]. CIESC Journal, 2013, 64(11): 4114-4120.

[20] LIGHTBODY G, IRWIN G W. Direct neural model reference adaptive control[J]. IEEE Proceedings—Control Theory and Applications, 1995, 142(1): 31-43.

[21] UPPAL A, RAY W H, POORE A B. On the dynamic behavior of continuous stirred tank reactors[J]. Chemical Engineering Science, 1974, 29(4): 967-985.

2015-10-10收到初稿，2016-04-19收到修改稿。

联系人及第一作者:李军（1969—），男，博士，教授。

Received date: 2015-10-10.

中图分类号:TP 273

文献标志码:A

文章编号:0438—1157（2016）07—2934—10

DOI:10.11949/j.issn.0438-1157.20151533

基金项目:国家自然科学基金项目（51467008）。

Corresponding author:Prof. LI Jun, lijun691201@mail.lzjtu.cn supported by the National Natural Science Foundation of China (51467008).

Adaptive control for a class of uncertain pure-feedback nonlinear systems using Backstepping based on extreme learning machine

LI Jun, SHI Qing
(College of Electrical Engineering and Automation, Lanzhou Jiaotong University, Lanzhou 730070, Gansu, China)

Abstract:For a class of uncertain pure-feedback nonlinear dynamical systems, an adaptive neural control method using the extreme learning machine (ELM) is presented on the basis of mean value theorem and Backstepping control. As a kind of single-hidden layer feed forward networks (SLFNs), ELM, which randomly chooses hidden node parameters and analytically determines the output weights, shows good generalized performance at extremely fast learning speed. In the process of each step for the Backstepping controller design, the ELM network is used to approximate unknown nonlinear part of the subsystem. Meanwhile, the adaptive adjustment law of weights parameter by Lyapunov stability analysis is derived so that the semiglobal uniform ultimate boundedness of all signals in the closed-loop nonlinear system can be guaranteed and the output of the system can also converge to a small neighborhood of the desired trajectory. The employed control method is then applied to the instance of continuous stirred tank reactor (CSTR) system in the chemical process and the simulation results are presented to verify the effectiveness of the method.

Key words:nonlinear dynamics; adaptive; control; Backstepping; extreme learning machine; neural networks