中空纤维膜外压全量过滤动态过程的数值模拟
2016-08-06庄黎伟戴干策
庄黎伟,戴干策
中空纤维膜外压全量过滤动态过程的数值模拟
庄黎伟,戴干策
(华东理工大学化学工程联合国家重点实验室,上海 200237)
摘要:建立了中空纤维膜外压式全量过滤的CFD模型,模拟膜丝长度、直径、渗透系数、装填密度、污染指数以及跨膜压差不同条件,得到通量分布和产水量的动态演变过程。研究结果表明:通量分布会随着过滤的进行而逐渐变得均匀,这种通量分布的自我调节作用在膜丝较长、较细,渗透性较好,装填密度较高,污染指数较高以及跨膜压差较高时更为明显;产水流量的倒数与累积产水量呈线性关系,但由于通量分布不均匀并且均匀性演变,这种线性关系区别于传统滤饼过滤模型;通过数据拟合得到了适用于中空纤维外压式全量操作的滤饼过滤关联式,可用于预测组件的性能和指导组件的设计。
关键词:中空纤维膜;计算流体力学;模型;数值模拟;通量分布;动态演变
引 言
中空纤维超滤膜组件凭借其自支撑、高装填密度、高比表面积[1]的优点,被广泛用于污水处理[2]和海水脱盐[3]等领域。然而,中空纤维膜组件的特殊结构会造成膜表面通量分布不均[4-7],从而减小膜面积利用率,缩短组件寿命。因此,有诸多学者进行了中空纤维膜组件内通量分布的研究。
早期研究主要采用的是模型外加辅助实验的方法:Chang等[8]通过建立浸没式中空纤维膜的渗透模型,发现通量沿膜丝长度的分布取决于膜丝内径、长度以及渗透性;在此基础上,他们先后研究了操作通量低于或高于临界通量下浸没式中空纤维膜组件的通量分布[9]以及全量操作下通量分布在过滤过程中的演变情况[10]。随着计算流体力学方法的兴起,越来越多膜研究者将其用于膜组件的设计和过程的优化[11]:Günther等以Happel的自由表面模型[12]为依据,将整个膜组件简化成由单根膜丝和包裹其外围的环状流体层,在此基础上分别研究了纯水过滤时装填密度对通量分布的影响[13]以及耦合滤饼过滤模型时装填密度对通量和滤饼分布的影响[14]。由此可知,中空纤维膜组件内通量分布不仅与膜丝本身性质有关,还会受膜丝装填以及污垢阻力的影响。由于中空纤维膜组件管程和壳程存在质量交换,交换过程由膜多孔介质层的流体渗透实现,渗透通量又与污垢阻力相互耦合,所以中空纤维膜组件内局部通量既存在空间上的分布,又随时间变化。中空纤维膜组件内通量分布的动态演变必然影响组件的产水性能,因而研究这种动态过程有助于深化理解中空纤维膜组件的过滤机理。虽然文献中存在中空纤维膜组件内通量分布动态演变的研究,但是缺乏对几何和操作参数影响的系统考量,从而无法建立通量分布动态演变与组件过滤性能的关系,所以本文的研究目的便在于此。
在前期的研究[4]中,分别采用解析模型和CFD模拟研究了中空纤维膜组件在外压式全量过滤时几何因素对通量分布以及能耗利用率的影响。本文在此基础上,考虑了滤饼阻力和局部通量的耦合,建立了新的中空纤维膜过滤CFD模型,描述在不同几何参数和操作条件下外压式全量过滤通量分布和产水流量的动态过程,并根据CFD模拟结果拟合出产水流量与累积产水量的关联式。
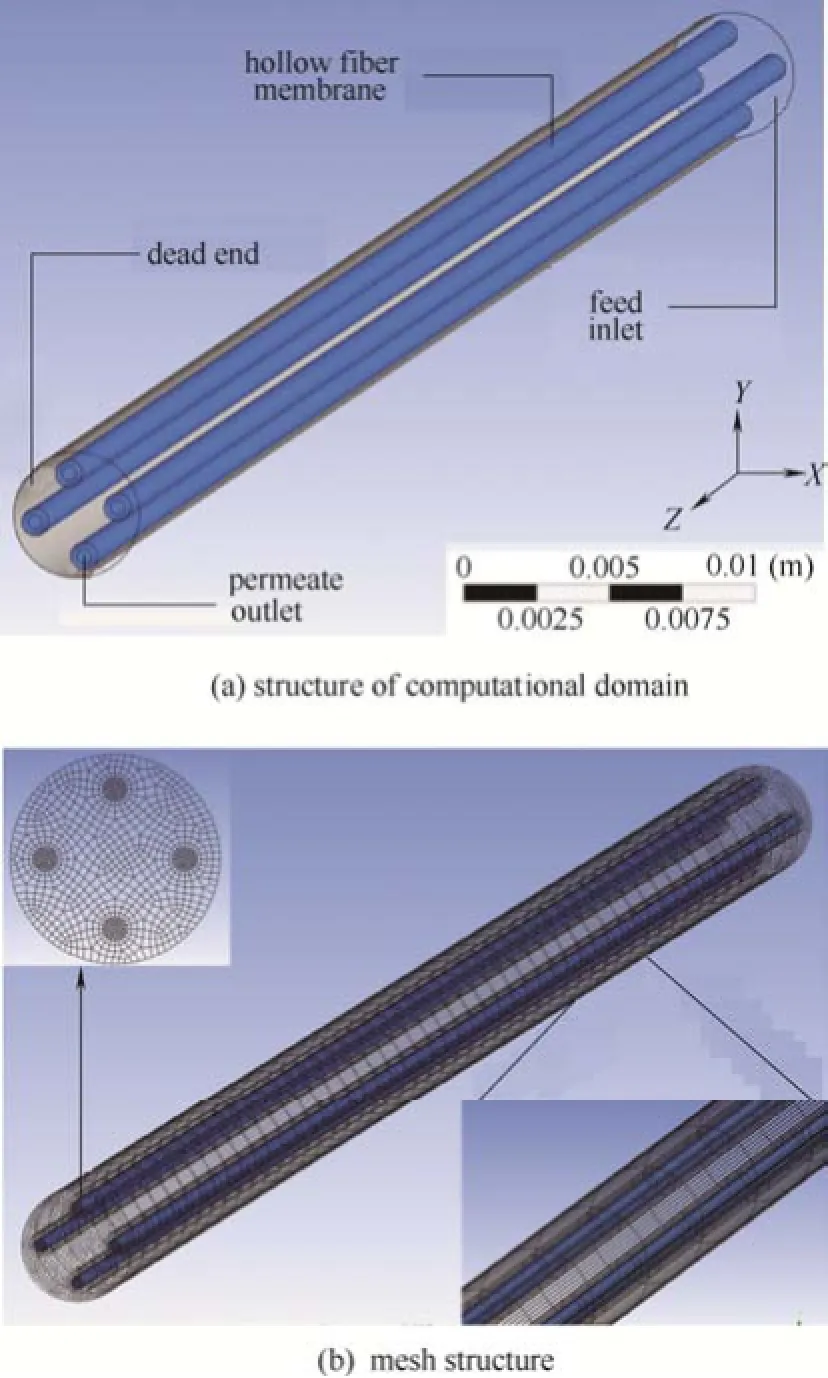
图1 中空纤维膜组件Fig.1 Hollow fiber membrane module
1 模型建立
1.1 物理模型
计算所用物理模型结构如图1(a)所示。4根长度为0.5 m,内外径分别为0.7和1.3 mm,渗透系数为4.9×10-16m2的中空纤维膜丝均匀装填于长为0.5 m、直径为6 mm的圆柱形壳体内,装填密度约为18.8%。原水由入口进入到壳程,在沿着轴向流动的同时,不断通过膜表面渗透至管程,由于是全量操作,原水全部转化为渗透液,并从管程出口离开。污垢全部截留在膜外表面,在渗透阶段,渗透阻力不断增大,直至进入洗涤阶段。跨膜压差为0.1 MPa,恒压操作。原水浓度为0.2 g·L-1,滤饼比阻为3×1014m·kg-1,忽略滤饼的可压缩性。在以上结构参数和操作参数的基础上,改变其中某一参数值,研究不同参数下过滤的动态特征。共考虑6个参数,分别为几何参数(膜丝长度、直径、渗透系数、装填密度)和操作参数(跨膜压差、污染指数),每种参数取7种情况,所有参数值列于表1。其中污染指数FI(fouling index)为原水浓度和滤饼比阻的乘积。在改变直径时,同时改变渗透系数,以保证不同直径膜丝的点跨膜阻力均为6.12×1011m-1,消除渗透系数的影响。在研究装填密度时,采用文献[4,13-14]的方法,保持膜丝尺寸不变,通过改变膜丝外围环形壳程空间大小来调节装填密度。
1.2 控制方程
在管程与壳程可认为是非定态层流不可压缩流动,因而连续性方程和动量方程分别为

式中,v为流体速度;ρ为流体密度;p为压强;μ为流体运动黏度。对于膜多孔介质区域,存在膜阻力和污垢阻力,对动量方程进行修正,得到多孔介质区域的连续性方程和动量方程
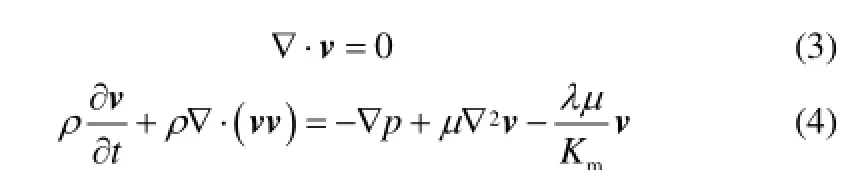
式中,λ为膜丝实体孔隙度,设定为 0.7;Km为多孔介质的渗透系数,且随着过滤的进行而不断降低。本文将污垢阻力等效成膜多孔介质阻力的增幅,该方法简化了污垢层的计算,推导过程如下。
根据阻力串联定律[14-15],任何一点通量J可以表示为

式中,Rm和 Rf分别为膜阻力和污垢阻力。对于污垢阻力,主要来源于污垢造成孔道阻塞、孔道收缩以及外层形成的滤饼。本文假设污垢颗粒大于膜孔径,所以污垢阻力仅为滤饼阻力。因此,污垢阻力Rf可以表示为[16]

式中,m为单位面积滤饼的质量;α为滤饼比阻。任意一点m随时间的变化关系可以表示为[16]
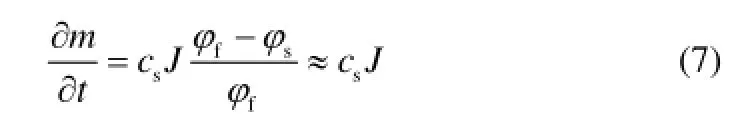
式中,cs为原水污垢质量浓度;φf和φs为滤饼层和原水中固体体积分数。由于全量过滤多用于低浓度污水处理,φf≫φs,所以有式(7)的简化。将微分形式的式(7)进行时间离散得到式(7)的差分形式,同时联立式(6),可以得到滤饼阻力在时间步长Δt内的增幅正比于t~(t+Δt)时段内该处的局部通量(由于时间步长很小,可认为该时段通量不发生变化),因而可以得到任意时刻任意点滤饼阻力与该处局部通量所有历史值之间的关系,最终任意点任意时刻通量可以表示为

式中,Δp为局部跨膜压差。此外,式(4)中膜的渗透系数可以表示为

式中,δ为膜多孔区域厚度。通过式(8)实现点通量和渗透阻力的耦合。理论上只要时间步长够小,联立式(1)~式(4)和式(10)就可以描述整个系统渗透的动态过程。
上述模型还基于以下假设:全量过滤时轴向速度较小,忽略平行于膜表面流动剪切对污垢的轴向输运作用,即污垢一旦与膜或滤饼接触便黏附;污垢与流体密度相近,跟随性好,忽略布朗扩散和惯性作用[14];忽略滤饼层对流动通道尺寸的影响,该假设在装填密度较低或者渗透周期较小时可认为合理。

表1 几何参数和操作参数Table 1 Geometric and operating parameters
1.3 边界条件和初始条件
如图1(a)所示,原水进口和渗透液出口分别设为压强入口和压强出口,其中出口处压强保持 0 MPa,进口处压强根据表1的跨膜压差而进行调整;计算域外围其他区域均设为无滑移壁面;计算域内部膜实体区设为多孔介质,仅考虑黏性阻力,阻力系数根据式(10)确定;多孔介质区域与管壳程交界面压强和速度连续,该种处理方法能定性描述交界面处滑移速度的轴向分布[4],优于文献惯用的速度无滑移处理[13-14]。初始时,内部速度和压强均设为0,原水在跨膜压差驱动下进入设备。
2 数值求解
2.1 方程离散与求解
计算域内整个流动过程,通过基于有限体积法的计算流体力学软件Fluent 6.3.26进行离散求解,压强速度以SIMPLE算法进行耦合,压强离散为二阶格式,动量离散为二阶迎风格式,求解过程中,压强、动量的亚松弛因子分别为 0.3、0.7。时间步长设为 10-3s,每个时间步内连续性和速度残差均低于10-5时进入下一时间步。先在纯水过滤过程中计算至流量稳定,1 s时开启污水过滤模式,计算至101 s,同时记录实时流量。多孔介质黏性阻力与流动的耦合通过自编程序(UDF)实现。求解过程通过两个Intel Xeon CPU和64 GB的DDR4型号内存完成。
2.2 网格与时间步长无关性
整个计算域均为结构化网格,以1.1节给出的特定尺寸的计算域为例,膜多孔介质区轴向均匀排布50个网格层,与管程和壳程一致,径向上有两个网格层,多孔介质区和壳程网格为六面体,管程均为五面体,如图1(b)所示。由图2可知,时间步长为10-3s时,网格数由48850增加至403100,1~100 s的产水量随时间的衰减曲线最大偏差在1%以内;同时,由图3可知,两种网格尺寸下1 s和100 s两个时刻点通量的轴向分布最大偏差也在 6%以内,可认为48850的网格数或相同网格尺寸下所得计算结果的数值误差在允许范围内。根据图2、图3可知,时间步长由10-3s减小至5×10-4s时,计算结果几乎无差别,可认为10-3s的时间步长足够捕捉过滤过程的动态特征。

图2 产水量随时间的变化Fig.2 Volumetric flow rate of permeate against time
3 结果与讨论
3.1 模型验证
首先,通过实验验证CFD模型在模拟纯水渗透方面的准确性,实验装置和操作细节见文献[4]。采用 5种长度中空纤维膜丝(其余膜丝细节与 1.1节一致)得出单根膜丝产水量随膜丝长度的变化关系,如图4所示,模拟结果与实验值相差在10%以内。

图3 点通量的轴向分布Fig.3 Flux distribution in axial direction
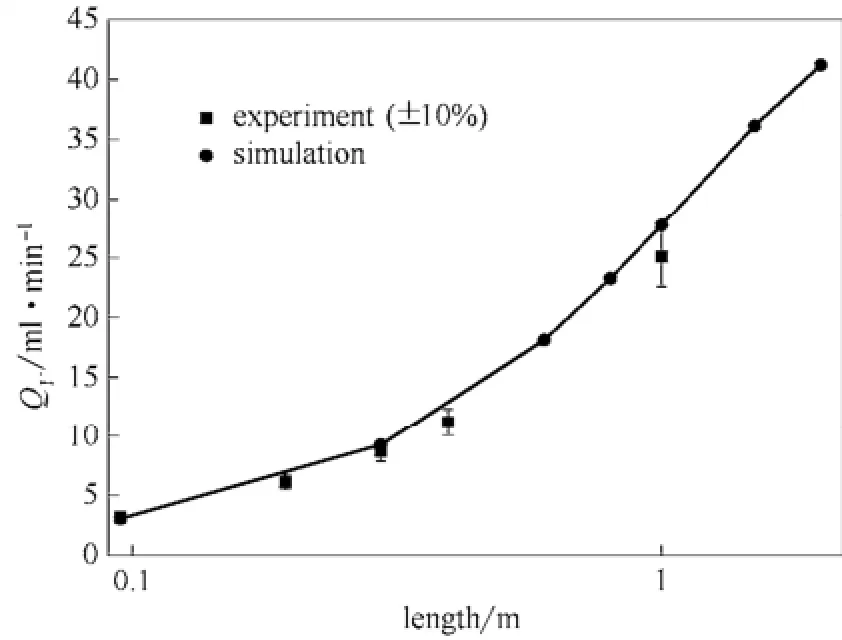
图4 单根膜丝产水速率随长度变化的实验值和模拟值Fig.4 Volumetric flow rate of single fiber with different length based on experiment and simulation

图5 组件跨膜压差随时间变化的模拟结果与文献结果[16]对比Fig.5 Comparison of trans-membrane pressure against time in present study and Ref. [16]
然后,参照文献[16]的中空纤维膜组件尺寸和操作参数,模拟了恒流量下跨膜压差随时间的变化关系,并与文献的模拟结果进行对比(图5),最大偏差在8%以内。需要指出的是,文献[16]考虑了滤饼厚度对壳程通道的影响,但是装填密度较低,可认为通道尺寸未发生明显变化,所以与本文的模拟细节一致。
因此,实验结果和文献结果验证了本文CFD模型的合理性。
3.2 压强场与速度场
图6、图7分别给出了组件内部的压强和速度分布,该图基于1.1节中几何和操作参数,过滤时间为101 s。由图6可知,壳程压强远高于管程,这是因为外压式过滤需要跨膜压差作为推动力;由图7可知,壳程速度逐渐降低,而管程速度逐渐升高,这由全量过滤壳程原水不断渗透至管程造成。由此可知,模拟所得压强和速度分布符合外压全量过滤流场特征。
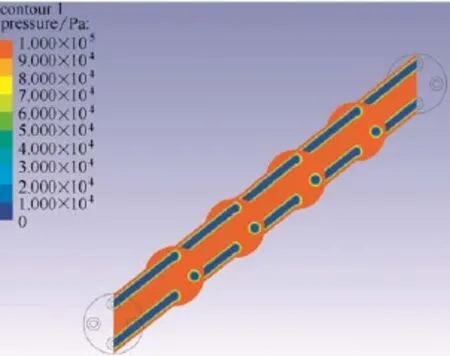
图6 压强分布Fig.6 Pressure distribution

图7 速度分布Fig.7 Velocity distribution
3.3 通量分布均匀性演变
图8(a)~(f)分别给出了不同膜丝长度、直径、渗透系数、装填密度、污染指数和跨膜压差(具体数值见表1)下,1 s、52 s和101 s等3个时刻通量分布的均匀性。6幅图中框出的数据均为基于 1.1节中几何参数和操作参数下模拟所得结果,除了图8(d)中装填密度为9.1%,低于其他图中的18.8%。通量分布均匀性采用轴向上量纲1局部通量的标准差SD表示

式中,J为平均通量。SD越高,通量分布均匀性越差。
由图8可知,随着过滤的进行,通量分布的均匀性有所提高,这种自我调节作用在许多文献[9,17]中都有提及。原因在于,初始局部通量较高的位置,滤饼形成速率高于初始局部通量较低区域,而滤饼形成速率对应着过滤阻力增加的速率,从而在一定的点跨膜压差分布下,局部通量高的区域通量降低速率更快,通量分布逐渐均匀。
对于t=1 s,即初始通量分布,由图8(a)、(b)可知,随着膜丝长度的增加和膜丝直径的减小,通量分布的初始均匀性逐渐降低,这是因为管程压降造成了局部跨膜压差沿膜丝长度逐渐增大,使靠近出口端的局部通量最高,靠近入口端的最低,这种分布从图3可以看出,并且这种不均匀性在较长[4]和较细[8]的膜丝中尤为明显。由图 8(c)可知,膜渗透系数越低,通量分布的初始均匀性越好,这是由于渗透系数越低意味着阻力越大,通道阻力的提高会一定程度削弱造成流动不均匀因素的影响[18-20],从而使流动分布更均匀,所以超滤、微滤膜中通量分布均匀性普遍差于纳滤以及反渗透。由图8(d)可知,通量分布的初始均匀性随着装填密度的增大先渐渐变好,然后急剧恶化。根据文献[4]的理论模型可知,中空纤维膜外压式全量过滤时局部通量沿轴向呈U形分布,当装填密度较小(低于约50%)时,局部通量最大值靠近出口端,而当装填密度较大时,膜丝进口端的局部通量会接近甚至超过出口端数值,这就解释了图8(d)的现象。但是可以看出,当装填密度低于68.1%时,通量分布的初始均匀性均在 0.01~0.02,差别不大。尤其是当装填密度低于40%时,可认为膜丝相互独立,此时装填密度的变化对组件通量分布[4]和产水量[13]没有明显影响。虽然低装填密度能防止通量分布均匀性的恶化,但是高装填密度却能提高膜组件在横截面的流动分布均匀性[19-20]。所以在组件膜丝装填密度的取舍上,应该选择合适的范围,例如文献[20]建议装填密度在30%左右以兼顾热质传递系数和压降损耗,而本文的建议范围是30%~68%以保证通量分布和组件横截面流动分布的均匀性。由图 8(f)可以看出,跨膜压差或者说是操作通量的增大会降低通量分布的初始均匀性,这与文献[7]所得结果一致,原因是高操作通量增大了管程的压降。

图8 几何和操作参数对瞬态通量分布均匀性的影响Fig.8 Effect of geometrical and operating parameters on uniformity of transient flux distribution
对于t=52 s和101 s,通过6幅图可以发现,通量分布初始均匀性差的提高幅度最大,比如图8(a)~(d)中的L7、D7、P1、PD7,或者是最大的污染指数或最大的跨膜压差会最大幅度提升通量分布均匀性,分别如图8(e)、(f)中的FI7和TMP7,由此说明,通量分布自我调节作用在初始均匀性较差或者较大污染指数或者较大跨膜压差(对应较大操作通量)下才更为明显。此外,开始的51 s(t=1~52 s)通量分布均匀性提高幅度远高于后期的49 s (t=52~101 s)。原因在于,初始通量分布十分不均匀,并且前期通量较高,滤饼生成速率越高,所以自我调节作用较为明显;而后期,由于通量分布均匀性已有明显提高,并且由于恒压操作,通量衰减至较小值,所以自我调节作用没有前期明显。
3.4 产水量演变
经典的滤饼阻力模型可以表示为[5,21]

式中,A为膜表面积;V为累积产水体积。然而,该模型只适用于平面式膜[3],并且,从模型表达式也可以看出,该模型只能描述局部滤饼形成过程或者通量和滤饼阻力分布完全均匀的情况,无法应用于本文的中空纤维膜系统。所以,本文将给出中空纤维膜系统的滤饼阻力模型,适用于存在通量和滤饼阻力分布及其均匀性演变的过程。

图9 不同几何和操作参数下dt/dV随V的变化Fig.9 dt/dV versus V under various geometrical and operating conditions
参照式(12),图9(a)~(f)分别给出了不同膜丝长度、直径、渗透系数、装填密度、污染指数和跨膜压差(具体数值见表1)条件下,6~101 s(隔5s取一次数值)中dt/dV随着渗透液累积体积V的变化。拟合结果表明,所有曲线都呈高度线性,说明通量和滤饼阻力分布及其均匀性演变并未改变dt/dV与 V的线性关系。所以,中空纤维膜系统内滤饼阻力模型可假设为

式中,a为斜率,b为截距。
图9说明,随着过滤的进行,产水累积总量越来越大,但产水流量会逐渐减小,图9中任意曲线上相邻两点间隔时间都为5 s,但点的距离却不断减小,也说明单位时间的产水量不断减小。这是因为恒定跨膜压差下,滤饼阻力的增大必然使产水流量逐渐减小。
图9中6幅图可以分为3类。
第1类是各曲线斜率不同,截距不同,比如图9(a)、(b)、(f)。截距等于初始或者纯水过滤体积流量的倒数,反映的是跨膜压差(推动力)和中空纤维膜组件结构(设备阻力)两者的作用结果;而斜率反映了跨膜压差(推动力)、组件结构(设备阻力)和污垢(过程阻力)三者的作用结果。在图9(a)、(b)中,随着膜丝增长和增粗,斜率和截距均不断减小。参照式(12)可知,膜表面积的增大均会降低曲线的斜率和截距,而膜丝增长和增粗正好对应面积的增大,说明中空纤维膜过滤产生滤饼的过程也有类似的规律。同样,图 9(f)中跨膜压差的增大也同时减小了斜率和截距,与式(12)给出的规律相同。
第2类是各曲线斜率相同,截距不同,比如图9(c)、(d)。在图 9(c)中,随着膜渗透系数的减小,或者说膜阻力的增大,截距不断增大,初始产水流量不断减小,也与式(12)规律相同。在图9(d)中,随装填密度的增大,截距逐渐增大,并且增大速率加快,说明过高装填度会显著降低产水流量,这与文献[13]所得结果一致。
第3类是各曲线截距相同,而斜率不同,比如图9(e)。在该图中,污染指数的增大提高了斜率,说明进料浓度或者滤饼比阻的增大都会加快产水量流量的衰减。
为了得到式(13)中a和b的表达式,首先取出图9中42条曲线的截距,通过数据拟合并参照文献[16]可知,截距b的表达式可以在该文献中纯水渗透表达式的基础上进行简单修正而得到;然后,取出图9中所有曲线的斜率,参照式(12)斜率的表达式并进行修正可以得到斜率a的表达式。最终
式(13)可以表示为

其中

式中,n为膜丝数量;Ai和Ae分别为单根膜丝内外表面积;di和de分别为内外径;g(ε)=,ε为壳程孔隙度,与装填密度之和为 1。通过与曲线(12)斜率比较可以发现,曲线(14)斜率跟膜的内外表面积以及内外径之比都有关系,说明中空纤维膜的圆环形结构以及管壳程流场都会使滤饼形成过程变得复杂,而无法采用模型(12)进行描述。图10给出了表1中所有几何和操作参数下任意V所对应dt/dV的模拟值与拟合式(14)所得数值的相对误差的平均值,吻合较好,说明关联式(14)能描述各种几何和操作参数下产水流量和累积产水量的关系。

图10 不同几何和操作参数下模拟与关联式(14)所得dt/dV的相对误差Fig.10 Relative error of dt/dV obtained from simulation to the one based on correlation Eq. (14) under various geometrical and operating conditions
4 结 论
本文建立了中空纤维膜外压式全量过滤 CFD模型,模拟展示了通量分布和产水体积流量的动态演变过程,并通过数据拟合得到了适用于中空纤维膜过滤的关联式,结果表明:
(1)中空纤维膜通量分布会随着过滤的进行逐渐变得均匀,这种自我调节作用在通量均匀性较差、产水流量较大以及进料浓度或滤饼比阻较大时更加明显;
(2)中空纤维膜外压式全量产水体积流量随过滤的进行逐渐减小,当污垢阻力主要为不可压缩滤饼阻力时,产水体积流量的倒数与累积产水量呈线性关系,但这种线性关系是基于通量分布不均匀以及均匀性存在演变的特性,区别于基于通量分布完全均匀假设的传统滤饼阻力模型,因而更能反映中空纤维膜组件过滤的产水特性;
(3)关联式(14)包含中空纤维膜组件的结构和操作参数,且适用于较宽的参数范围,因而可用于预测特定结构下组件的产水性能,并指导组件的优化设计;同时,本文的CFD模型在模拟计算时耗费计算资源较少,有望用于大型中空纤维膜组件过滤过程的模拟,这部分工作将在后期的研究中开展。
符 号 说 明
A ——膜面积,m2
Ae——膜外表面积,m2
Ai——膜内表面积,m2
cs——原水污垢质量浓度,kg·m-3
de——膜丝外径,mm
di——膜丝内径,mm
J ——渗透通量,m·s-1
Km——膜渗透系数,m2
L ——膜丝长度,m
m ——单位面积滤饼的质量,kg·m-2
n ——膜丝数量
p ——静压强,MPa
Δp ——局部跨膜压差,MPa
QV——体积流量,m3·s-1
Rf——污垢阻力,m-1
Rm——膜阻力,m-1
TMP ——总跨膜压差,MPa
t ——时间,s
α ——滤饼比阻,m·kg-1
δ ——膜厚度,mm
ε ——膜丝束壳程空隙度
λ ——膜丝孔隙度
μ ——动力黏度,Pa·s
ρ——密度,kg·m-3
ϕf——原水固体体积分数
ϕs——滤饼层固体体积分数
References
[1] YANG X, WANG R, FANE A G, et al. Membrane module design and dynamic shear-induced techniques to enhance liquid separation by hollow fiber modules: a review [J]. Desalination and Water Treatment, 2013, 51 (16/17/18): 3604-3627.
[2] DELGADO S, DIAZ F, VERA L, et al. Modelling hollow-fibre ultrafiltration of biologically treated wastewater with and without gas sparging [J]. Journal of Membrane Science, 2004, 228 (1): 55-63.
[3] LI N N, FANE A G, HO W W, et al. Advanced Membrane Technology and Applications [M]. New Jersey: John Wiley & Sons, 2011: 47-242.
[4] ZHUANG L W, GUO H F, WANG P H, et al. Study on the flux distribution in a dead-end outside-in hollow fiber membrane module [J]. Journal of Membrane Science, 2015, 495: 372-383.
[5] KIM J, DIGIANO F A. Defining critical flux in submerged membranes: influence of length-distributed flux [J]. Journal of Membrane Science, 2006, 280 (1): 752-761.
[6] LI X H, LI J X, WANG J, et al. Experimental investigation of local flux distribution and fouling behavior in double-end and dead-end submerged hollow fiber membrane modules [J]. Journal of Membrane Science, 2014, 453: 18-26.
[7] LI X H, LI J X, WANG H, et al. A filtration model for prediction of local flux distribution and optimization of submerged hollow fiber membrane module [J]. AIChE Journal, 2015, 61 (12): 4377-4386.
[8] CHANG S, FANE A G. The effect of fibre diameter on filtration and flux distribution—relevance to submerged hollow fibre modules [J]. Journal of Membrane Science, 2001, 184 (2): 221-231.
[9] CHANG S, FANE A G, VIGNESWARAN S. Modeling and optimizing submerged hollow fiber membrane modules [J]. AIChE Journal, 2002, 48 (10): 2203-2212.
[10] CHANG S, FANE A G, WAITE T D. Analysis of constant permeate flow filtration using dead-end hollow fiber membranes [J]. Journal of Membrane Science, 2006, 268 (2): 132-141.
[11] GHIDOSSI R, VEYRET D, MOULIN P. Computational fluid dynamics applied to membranes: state of the art and opportunities [J]. Chemical Engineering and Processing: Process Intensification, 2006, 45 (6): 437-454.
[12] HAPPEL J. Viscous flow relative to arrays of cylinders [J]. AIChE Journal, 1959, 5 (2): 174-177.
[13] GÜNTHER J, SCHMITZ P, ALBASI C, et al. A numerical approach to study the impact of packing density on fluid flow distribution in hollow fiber module [J]. Journal of Membrane Science, 2010, 348 (1): 277-286.
[14] GÜNTHER J, HOBBS D, ALBASI C, et al. Modeling the effect of packing density on filtration performances in hollow fiber microfiltration module: a spatial study of cake growth [J]. Journal of Membrane Science, 2012, 389: 126-136.
[15] TANSEL B, BAO W Y, TANSEL I N. Characterization of fouling kinetics in ultrafiltration systems by resistances in series model [J]. Desalination, 2000, 129 (1): 7-14.
[16] SERRA C, CLIFTON M J, MOULIN P, et al. Dead-endultrafiltration in hollow fiber modules: module design and process simulation [J]. Journal of Membrane Science, 1998, 145 (2): 159-172.
[17] MENDRET J, GUIGUI C, CABASSUD C, et al. Numerical investigations of the effect of non-uniform membrane permeability on deposit formation and filtration process [J]. Desalination, 2010, 263 (1/2/3): 122-132.
[18] ZHANG L Z. Flow maldistribution and performance deteriorations in membrane-based heat and mass exchangers [J]. Journal of Heat Transfer, 2009, 131 (11): 111801.
[19] ZHANG L Z, LI Z X, ZHONG T S, et al. Flow maldistribution and performance deteriorations in a cross flow hollow fiber membrane module for air humidification [J]. Journal of Membrane Science, 2013, 427: 1-9.
[20] LI Z X, ZHANG L Z. Flow maldistribution and performance deteriorations in a counter flow hollow fiber membrane module for air humidification/dehumidification [J]. International Journal of Heat and Mass Transfer, 2014, 74: 421-430.
[21] CHELLAM S, JACANGELO J G, BONACQUISTI T P. Modeling and experimental verification of pilot-scale hollow fiber, direct flow microfiltration with periodic backwashing [J]. Environmental Science & Technology, 1998, 32 (1): 75-81.
2016-01-19收到初稿,2016-03-09收到修改稿。
联系人:戴干策。第一作者:庄黎伟(1988—),男,博士研究生。
Received date: 2016-01-19.
中图分类号:TP 273
文献标志码:A
文章编号:0438—1157(2016)07—2841—10
DOI:10.11949/j.issn.0438-1157.20160088
Corresponding author:Prof. DAI Gance, gcdai@ecust.edu.cn
Numerical simulation of dynamic process during outside-in dead-end filtration in hollow fiber membrane module
ZHUANG Liwei, DAI Gance
(State Key Laboratory of Chemical Engineering, East China University of Science and Technology, Shanghai 200237, China)
Abstract:A CFD model was developed based on the filtration in the dead-end outside-in hollow fiber membrane module. Various fiber length, diameter, permeability, packing density, fouling index and transmembrane pressure were chosen during numerical simulation of the dynamic evolution of flux distribution and permeate volumetric flow rate. The simulation revealed that the uniformity of flux distribution improved as the filtration processes. The self-adjustment of the flux distribution was more pronounced with longer, narrower, more permeable fibers, higher packing density, fouling index and trans-membrane pressure. The inverse of the water volumetric flow rate increased linearly with the accumulated volume of the permeate. Due to the non-uniformity of the flux distribution and its dynamic evolution, the linear relationship differed from the one presented in the classic cake filtration model. A correlation equation to characterize the dead-end outside-in cake filtration in the hollow fiber membrane module was obtained through curve fitting of the simulation data. The equation enabled the prediction of the module performance and better design of the module.
Key words:hollow fiber membrane; CFD; model; numerical simulation; flux distribution; dynamic evolution
