CFD-DEM模型并行化及其在流化床气固流动中的应用
2016-08-06杨春振陈成敏刘光霞段钰锋
杨春振,陈成敏,刘光霞,段钰锋
CFD-DEM模型并行化及其在流化床气固流动中的应用
杨春振1,陈成敏1,刘光霞1,段钰锋2
(1山东省科学院能源研究所,山东 济南 250014;2东南大学能源与环境学院能源热转换及其过程测控教育部重点实验室,江苏 南京 210096)
摘要:提出广义区域覆盖法用于定位计算节点区域,利用Fluent软件的UDFs实现颗粒信息在计算节点间高效、准确地传递,建立了适用于非正交网格的CFD-DEM模型并行求解方法,在探讨并行模型计算效率的基础上对埋管流化床和单孔射流流化床内的气泡行为及双支腿流化床半床间的颗粒交换行为进行了数值模拟研究并对比实验结果。结果表明:CFD-DEM模型并行求解方法能够快速传递及收集计算节点内的颗粒信息;广义区域覆盖法降低了颗粒在计算节点内的定位时间,提高了模型的并行计算效率;能够捕获与 Rong等一致的埋管周围气泡行为(其频率约为3 Hz),获得了与Bokkers等结果接近的单孔射流气泡尺寸及颗粒速度矢量分布,双支腿流化床半床间颗粒交换行为与实验结果一致,第一主频约为1 Hz,第二主频大于2 Hz。
关键词:并行;DEM模型;两相流;流化床;数值模拟
引 言
CFD-DEM(computational fluid dynamic and discrete element method)模型是目前研究稠密气固两相流流动、传热等的重要工具[1-5]。随着气固装置(如流化床)几何形状复杂度的提高,诸多学者提出了不同方法实现DEM模型在非正交网格内的使用。Wu等[6-7]提出了精确计算三角形网格和楔形网格内空隙率的方法;赵永志等[8-9]以正交DEM网格作为背景网格完成了DEM模型与Fluent软件的耦合,并研究了埋管流化床的传热行为;Su等[10]将DEM模型与OpenFOAM耦合,研究了多埋管流化床内的颗粒流动行为;杨旭[11]借鉴光滑粒子动力学中插值的思想和权函数的概念实现了 DEM在非规则网格内的使用;本课题组[12-13]提出二维和三维通用的区域覆盖法(domain coverage method, DCM),实现了颗粒在非正交网格内的高效定位技术,大大提高了 DEM 模型在非规则网格内的应用。
随着流化床尺寸的增加或颗粒粒径的减小,CFD-DEM模型需要跟踪的颗粒量急剧增加,采用串行程序会增加计算量。为了有效解决这一问题,研究者着力于开发 CFD-DEM模型的并行算法。Tsuji等[14]利用16个CPU研究了三维方形流化床内4.5×106个颗粒的气泡行为;Xu等[15]开发出多尺度CPU-GPU计算模式,采用CPU计算流场、GPU计算颗粒运动的方式模拟了工业流化床内的气固流动行为;任立波等[16]借助Fluent软件的MPI技术实现了CFD-DEM模型的并行耦合算法;Wu等[17]借助Fluent软件在并行计算方面的优势发展出一套颗粒在多计算节点间信息传递的方法,实现了DEM模型的并行化。
本研究在所提出的DCM方法基础上提出广义DCM方法,借助Fluent软件提供的用户自定义宏函数(user defined function,UDF)实现了CFD-DEM模型的并行化。首先介绍实现颗粒在多计算节点间信息传递的方法,借助广义DCM实现CFD-DEM模型的并行计算;然后数值模拟研究了单埋管流化床和单孔射流流化床的气泡特性及双支腿半床间颗粒交换行为,并与相关学者的实验研究结果进行对比,验证了所开发的CFD-DEM模型并行计算方法的准确性。本研究所使用的CFD-DEM数学模型与文献一致,见文献[12-13, 18-19]。
1 并行CFD-DEM模型
1.1 计算节点间颗粒信息的传递
Fluent软件具有高效的并行计算能力,其提供的 UDF不仅可以实现复杂数学模型的建模,也可通过 Host与 Node间的信息交互 UDF(如PRF_CSEND_###及PRF_CRECV_###等)实现模型的并行化。
CFD-DEM模型并行计算要求Fluent流体网格分布于至少2个Node内,由于每个DEM时间步长内颗粒位置均发生改变,需将各节点内的颗粒信息发送给Host统计并重新分配至其应属的Node。因此,提高颗粒信息的再分配效率是提高 CFD-DEM模型并行化速度的重点。
图1为Fluent流体网格在不同Node内的分布。Node 0包含全局网格的1~4列,其中1~3列为内部网格、4列为外部网格(用于 Node间的信息传递);Node 1包含全局网格的3~7列,其中4~7列为内部网格、3列为外部网格。位于Node内部网格的颗粒与分布在全部网格的颗粒必须是时刻相同的,因此为了获得全部颗粒信息同时保证不重复,可以将Node内部网格内的颗粒信息传递给Host统计,并通过host_to_node_###函数实现Host向Node分配颗粒信息的功能;为了保证Node内颗粒碰撞的准确性和完整性,需检测内部和外部网格内所有颗粒间是否发生碰撞。

图1 GDCM基本原理Fig. 1 Schematic diagram of GDCM Mesh splitting line; GDCM grid boundary; Fluent grid boundary;particle; particle locate in GDCM grid
为了实现Host将汇总到的颗粒重新合理、高效地分配至Node,本研究基于DCM提出广义区域覆盖法(general DCM,GDCM):首先建立如图1所示的GDCM网格(GDCC),分析各Fluent流体网格节点坐标获得各坐标方向上的最大值和最小值,最终确定各节点的计算区域,Host搜集位于该区域内的颗粒并将其信息传递给Node;然后在Node内利用DCM方法定位颗粒在Fluent网格内的位置,用于网格空隙率的计算,DCM可见文献[12]。DCM关键在于建立单个Fluent流体网格和多个DEM网格间的对应关系;GDCM借助DCM覆盖网格的思路,重点在于确定节点内所有Fluent网格的区域,并形成各计算节点区域的覆盖网格。
图 2为 CFD-DEM模型并行化流程图,采用User defined Init、User defined EXECUTE_AT_END 和User defined Adjust这3个UDF实现。User defined Init用于在 Host中初始化颗粒信息,确定各 Node 的GDCC、建立DEM网格和DCC,确定DEM网格与Fluent网格的映射关系;User defined EXECUTE_AT_END可控制流体和颗粒时间步长(Δtg和Δtp),当Δtp<Δtg时判断DEM模型的执行次数;User defined Adjust实现DEM模型功能,包括颗粒定位、网格空隙率、颗粒曳力、碰撞检测、计算接触力及颗粒跟踪等。
各Node的颗粒信息经过一个时间步长更新后汇总发送至Host。Host将颗粒信息汇总并存储,借助GDCC重新确定颗粒所属的Node,通过消息传递UDF将颗粒信息回传至Node。

图2 CFD-DEM模型并行算法流程Fig. 2 Flowchart of parallel CFD-DEM algorithm
1.2 并行CFD-DEM模型计算效率
为了定量对比并行算法和串行算法的效率,本研究测试了如图3(a)所示的0.1 m×0.1 m区域(戴尔:i3-2370M)内颗粒定位所耗时间,其中串行算法耗时为全部颗粒定位于各Fluent流体网格内的时间,并行算法耗时包括Host将汇总的颗粒信息传递给Node的时间及颗粒定位于各Node的Fluent网格的时间。颗粒总数分别为1万、4万和16万个。按照图3(a)所示颗粒排列方案,并行模型2个Node的颗粒数分别为0.52万、2.08万和8.32万个。从图3(b)所示的颗粒定位耗时可以看出定位颗粒所需时间随颗粒数增加而增加。定位16万个颗粒时,2个Node的耗时分别为46 ms和51 ms,串行算法需84 ms,可见CFD-DEM模型的并行算法计算效率更高。
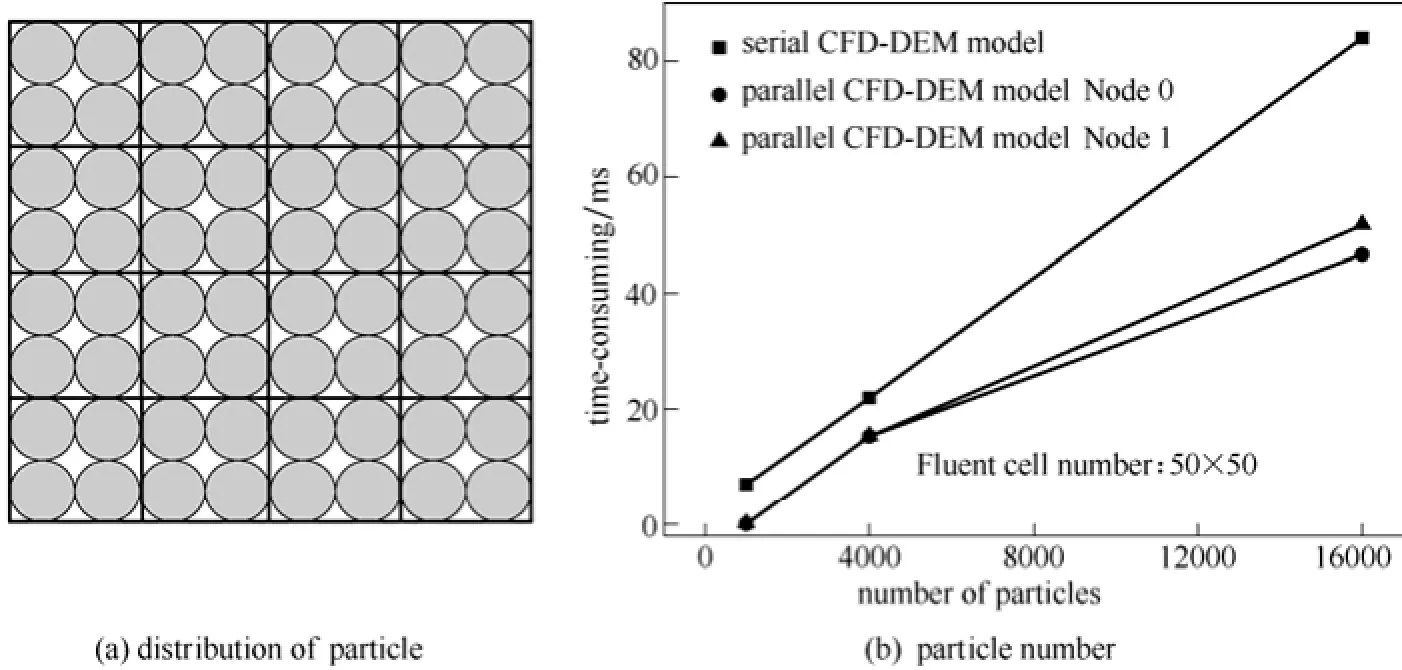
图3 颗粒数对定位颗粒耗时的影响Fig. 3 Effects of particle number on time-consuming
2 二维单埋管流化床气泡行为
为了验证并行化的CFD-DEM模型的准确性,采用串行与2个Node的并行CFD-DEM模型分别计算了单埋管流化床气泡行为,并与Rong等[18]的结果进行对比。图4(a)给出了二维单埋管流化床几何结构,宽和高分别为180mm和420mm,埋管直径为30 mm,采用非规则网格划分,网格数为8262个。本研究模拟20000个颗粒,采用重力沉降法获得颗粒的初始分布,如图4(c)所示。流化风通过在布风板上设置的20个Φ3 mm孔进入流化床,采用速度入口边界条件(u=1.1 m·s-1)、充分发展出口边界条件。
串行模型的DEM网格数为180×210。由于并行计算区域边缘呈锯齿状,并行模型2个Node分别设置90×210个DEM网格。模拟物理时间为5 s。表1列出了模拟参数,DEM模型见文献[18]。

表1 模拟参数Table 1 Simulation parameters

图4 二维单埋管流化床Fig. 4 2D fluidized bed with single immersed tube
图 5给出了采用串行 CFD-DEM模型和并行CFD-DEM模型获得的埋管右侧水平位置为基准上下2°范围内空隙率随时间的变化。从图中可以看出串行模型和并行模型均出现空隙率为1的时间段,这表明此时大气泡穿过埋管,而且完全包裹住埋管,阻碍颗粒与埋管发生碰撞。在空隙率不为1的时间段(由于采用质心定位法及拟三维法求解空隙率,图中呈现出空隙率小于 0.25的情形),呈现小气泡流动、颗粒包裹埋管及两种并存的3种阶段。
为了定量分析气泡生成、破碎的周期行为,对图5中的空隙率变化进行功率谱密度(PSD)分析,如图6所示。串行算法和并行算法获得的气泡频率分别为3.084 Hz和3.203 Hz,与Rong等[18](u=1.0 m·s-1)计算的2~3 Hz是相符的。

图5 埋管右侧上下2°范围内空隙率随时间的变化Fig. 5 Variations of void fraction at ±2° of right-side of tube simulated by serial and parallel CFD-DEM models
3 三维单孔射流流化床气泡行为
本研究模拟了三维矩形单孔射流流化床内的气泡行为,并与 Bokkers等[19]的实验和数值模拟结果进行对比。流化床宽深高分别为0.15 m、0.015 m、0.45 m;采用正交结构化网格划分,网格数为4050个;喷口宽10 mm,入口速度为20 m·s-1,流化速度为1.2 m·s-1。模拟3万个粒径为2.5 mm的颗粒。为了精确计算颗粒碰撞过程,颗粒运动的时间步长设为2×10-6s。采用2个Node。表2列出了模拟参数。本研究采用的CFD-DEM模型与文献[19]一致。
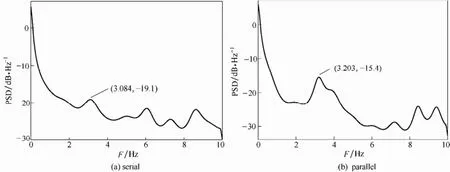
图6 对随时间变化的空隙率的功率谱密度分析Fig. 6 PSD analysis of variations of void fraction

表3 模拟参数Table 2 Simulation parameters
图7对比了t=150 ms时刻本研究并行算法获得的气泡与Bokkers等串行算法的模拟及实验结果。对比图7(a)和图 7(c)可以看出,本研究模拟得到的气泡较 Bokkers等的模拟结果小(本研究采用 De Felice曳力模型;Bokkers等采用Ergun/Wen-Yu曳力模型)。然而对比图 7(a)与图 7(b)所示的实验结果,本研究模拟结果与实验气泡相似。
为了定量描述射流气泡行为,图8给出了并行模拟和Bokkers等实验获得的气泡尺寸及其周围颗粒的速度分布。并行模拟的最大处的气泡尺寸约为80 mm×150 mm,实验得到的气泡尺寸约为 77 mm×120 mm,两者尺寸在高度方向存在较大的差别,但在宽度方向基本相同。此外,结合颗粒的速度矢量分布可以看出本研究并行算法能够在细节上较为准确地捕获气泡周围颗粒的运动规律,如气泡上部周围颗粒及其速度矢量分布一致性较好。但并行模拟结果在气泡顶端及气泡尾涡区域与实验结果存在一定的差异,这与颗粒的碰撞参数及曳力模型的选择有关。

图7 单孔射流气泡 (t=150 ms)Fig. 7 Bubble in single jet fluidized bed at t=150 ms
4 二维双支腿流化床颗粒交换行为
双支腿结构是大型循环流化床锅炉的一种重要设计方案,然而如果操作不当半床间易发生不稳定的颗粒交换并造成“翻床”现象。本课题组采用Yule-Walker方法对双支腿流化床(dual leg fluidized bed,DL-FB)半床间的压力脉动信号进行功率谱分析,研究颗粒交换的主频及其对应的物理特性[20],并采用CFD-DEM模型串行求解方法模拟了半床间的颗粒交换行为[13]。为进一步验证本研究并行求解方法的准确性,采用4个Node模拟颗粒交换行为。
图9给出了DL-FB的几何尺寸、网格分布(网格共10240个)以及重力沉降法获得的颗粒初始分布。双支腿入口气体流速为4.16 m·s-1,顶部出口气体充分发展,床料高80 mm,模拟时间为60 s。表3列出了模拟参数。

图9 双支腿流化床Fig. 9 Dual leg fluidized bed

表3 模拟参数Table 3 Simulation parameters

图8 气泡尺寸及气泡周围颗粒的速度矢量分布Fig.8 Bubble size and velocity vectors of solids
图10(a)为60 s内DL-FB半床内颗粒数(Np)的变化,可以看出颗粒在半床间发生剧烈的交换,而且呈现出两种明显的交换行为:颗粒数变化尖峰(颗粒以团簇的形式交换)、较缓和区域(颗粒以单颗粒的形式交换)并存。这与本课题组[20]的实验结果一致。为了定量分析两种行为的频率及强度,图10(b)给出了颗粒数变化的PSD图,可以看出存在两个主频,分别为1.152 Hz和2.324 Hz,这与实验得到的0.938 Hz和2.792 Hz[20]基本一致。

图10 DL-FB半床间颗粒交换行为及功率谱分析Fig. 10 Solid exchange behavior and PSD diagram in DL-FB
5 结 论
本研究提出广义区域覆盖法,借助Fluent软件的用户自定义函数实现颗粒信息在多计算节点间的快速、准确传递,建立了可适用于非规则网格的CFD-DEM模型并行求解方法。在对比了并行算法与串行算法的计算效率基础上,为了验证并行化CFD-DEM模型的计算精度,对比分析了单埋管流化床和单孔射流流化床内的气泡行为以及双支腿流化床内的颗粒交换行为,并采用功率谱分析方法定量获得了信号的脉动频率。结论如下。
(1)广义区域覆盖法能够快速将颗粒分配至多计算节点内;并行化CFD-DEM模型能够高效地保证颗粒信息在Host及Node间传递。
(2)模型并行算法具有较高的计算效率,双Node并行计算效率约为串行模型的1.6~1.8倍。
(3)并行化CFD-DEM模型能够较好地捕获流化床埋管周围的气泡行为,埋管周围气泡频率约为3 Hz;获得了与Bokkers等实验结果一致的单孔射流气泡尺寸及颗粒速度矢量;双支腿流化床半床间颗粒交换行为存在两个主频,数值模拟得到的第一、二频率分布与实验结果一致。
符 号 说 明
d——直径,m
e——颗粒碰撞恢复系数
F——频率,Hz
k——弹性系数,N·m-1
PN——颗粒数,个
t——时间,s
Δt——时间步长,s
u——速度,m·s-1
α——空隙率
μg, μpp, pw——分别为气体黏度和颗粒摩擦系数
ρ ——密度,kg·m-3
下角标
g——气体
n——法向
p——颗粒
t——切向
References
[1] 彭丽, 吴迎亚, 李佳瑶, 等. 基于 DEM 模拟气固鼓泡床中颗粒碰撞参数对流场间歇性的影响[J]. 化工学报, 2015, 66(6): 2041-2048.
PENG L, WU Y Y, LI J Y, et al. Effect of granular collision parameters on DEM simulation of flow field intermittency in gas-solids bubbling fluidized bed [J]. CIESC Journal, 2015, 66(6): 2041-2048.
[2] 王猛, 朱卫兵, 孙巧群, 等. 提升管内气固流动特性的离散元模拟[J]. 化工学报, 2013, 64(7): 2436-2445.
WANG M, ZHU W B, SUN Q Q, et al.. Discrete element simulation of gas-solids flow behavior in riser[J]. CIESC Journal, 2013, 64(7): 2436-2445.
[3] 周池楼, 赵永志. 离散单元法及其在流态化领域的应用[J]. 化工学报, 2014, 65(7): 2520-2534.
ZHOU C L, ZHAO Y Z. Discrete element method and its applications in fluidization[J]. CIESC Journal, 2014, 65(7): 2520-2534.
[4] 卜昌盛, 陈晓平, 刘道银, 等. 基于颗粒尺度的离散颗粒传热模型[J]. 化工学报, 2012, 63(3): 698-704.
BU C S, CHEN X P, LIU D Y, et al. Heat transfer model for particles with dicrete element method[J]. CIESC Journal, 2012, 63(3): 698-704.
[5] 吴迎亚, 蓝兴英, 高金森. 基于DEM模拟的气固鼓泡床内流场间歇性及颗粒相干结构的分析[J]. 化工学报, 2014, 65(7): 2724-2732.
WU Y Y, LAN X Y, GAO J S. Analysis of flow field intermittencyand coherent structure of particles based on DEM simulation of gas-solids bubbling bed[J]. CIESC Journal, 2014, 65(7): 2724-2732.
[6] WU C L, BERROUK A S, NABDAJYMAR K. Three-dimensional discrete particle model for gas-solid fluidized beds on unstructured mesh[J]. Chemical Engineering Journal, 2009, 152(2/3): 514-529.
[7] WU C L, ZHAN J M, LI Y S, et al. Accurate void fraction calculation for three-dimensional discrete particle model on unstructured mesh[J]. Chemical Engineering Science, 2009, 64(6): 1260-1266.
[8] ZHAO Y Z, JIANG M Q, CHENG Y. Particle-scale simulation of the flow and heat transfer behaviors in fluidized bed with immersed tube[J]. Frontiers of Chemical Engineering in China, 2008, 2(3): 341-345.
[9] 赵永志, 程易. 沉浸管式流化床的颗粒尺度模拟[J]. 化学工程, 2007, 35(11): 21-24.
ZHAO Y Z, CHENG Y. Particle-scale simulation of fluidized bed with immersed tubes[J]. Chemical Engineering (China), 2007, 35(11): 21-24.
[10] SU J W, GU Z L, XU X Y. Discrete element simulation of particle flow in arbitrarily complex geometries[J]. Chemical Engineering Science, 2011, 66(23): 6069-6088.
[11] 杨旭. 微型流化床的数值模拟及混合特性研究[D]. 长春: 吉林大学, 2014.
YANG X. Numerical simulation on the mixing characteristics in micro fluidized bed[D]. Changchun: Jilin University, 2014.
[12] 杨春振, 段钰锋, 孙荣峰, 等. 埋管流化床颗粒流动行为的数值模拟[J]. 化工学报, 2013, 64(8): 2788-2793.
YANG C Z, DUAN Y F, SUN R F, et al. Numerical study of solid behavior in a fluidized bed with multi-immersed tubes[J]. CIESC Journal, 2013, 64(8): 2788-2793.
[13] YANG C Z, DUAN Y F. CFD-DEM model for simulating solid exchange in a dual-leg fluidized bed[J]. Chemical Engineering & Technology, 2013, 36(11): 1907–1914.
[14] TSUJI T, YABUMOTO K, TANAKA T. Spontaneous structures in three-dimensional bubbling gas-fluidized bed by parallel DEM–CFD coupling simulation[J]. Powder Technology, 2008, 184(2): 132-140.
[15] XU M, CHEN F G, LIU X H, et al. Discrete particle simulation of gas-solid two-phase flows with multi-scale CPU-GPU hybrid computation[J]. Chemical Engineering Journal, 2012, 207/208: 746-757.
[16] 任立波, 韩吉田. 基于 CFD-DEM 耦合并行算法的锥形喷动床内离散颗粒数值模拟[J]. 东南大学学报(自然科学版), 2014, 44(5): 993-998.
REN L B, HAN J T. Numerical simulation of discrete particles in conical-base spouted bed based on parallel coupled CFD-DEM model[J]. Journal of Southeast University (Natural Science Edition), 2014, 44(5): 993-998.
[17] WU C L, AYENI O, BERROUK A S, et al. Parallel algorithms for CFD-DEM modeling of dense particulate flows[J]. Chemical Engineering Science, 2014, 118: 221-244.
[18] RONG D G, TAKAFUMI M, MASAYUKI H. Particle and bubble movements around tubes immersed in fluidized beds — a numerical study[J]. Chemical Engineering Science, 1999, 54(23): 5737-5754.
[19] BOKKERS G A, VAN SINT ANNALAND M, KUIPERS J A M. Mixing and segregation in a bidisperse gas-solid fluidised bed: a numerical and experimental study[J]. Powder Technology, 2004, 140(3): 176-186.
[20] YANG C Z, DUAN Y F, HU H T, et al. Pressure fluctuation analysis of solid exchange in a dual-leg fluidized bed[J]. Powder Technology, 2012, 224(224): 69-75.
2016-01-07收到初稿,2016-03-14收到修改稿。
联系人:陈成敏。第一作者:杨春振(1984—),男,博士。
Received date: 2016-01-07.
中图分类号:TK 1
文献标志码:A
文章编号:0438—1157(2016)07—2748—08
DOI:10.11949/j.issn.0438-1157.20160026
基金项目:山东省自主创新及成果转化专项(2014ZZCX04215);山东省科学院青年基金项目(2014QN016,2013QN016)。
Corresponding author:CHEN Chengmin, chencm@sderi.cn supported by the Project of Independent Innovation and Achievement Transformation of Shandong Province (2014ZZCX04215) and the Youth Fund of Shandong Academy of Sciences (2014QN016, 2013QN016).
Parallel algorithm of CFD-DEM model and applications on gas-solids flow in fluidized beds
YANG Chunzhen1, CHEN Chengmin1, LIU Guangxia1, DUAN Yufeng2
(1Energy Research Institute of Shandong Academy of Sciences, Jinan 250014, Shandong, China;2Key Laboratory of Energy Thermal Conversion and Control, Ministry of Education, School of Energy and Environment, Southeast University, Nanjing 210096, Jiangsu, China)
Abstract:General domain coverage method (GDCM) was proposed to determine the region for each computing node efficiently by comparing all cell nodes, where these regions were helpful for Host to identify which computing node solid particle belongs to. Particle information was passed among host and nodes with the help of Fluent UDFs. The parallel algorithm for CFD-DEM model was developed successfully to simulate gas-solids flows in the fluidized beds (FBs) which were meshed in arbitrary shapes. Based on the comparison of calculation efficiency between parallel algorithm and serial algorithm, the bubble behaviors were studied in a FB with an immersed tube in a single jet FB, and the solids exchange behaviors between two half beds were simulated and compared with experimental results in a dual leg FB. The simulation results showed that the particle information was passed between host and nodes efficiently by parallel algorithm. It was efficient for GDCM to determine which computing node particles are in. The simulated bubbling frequency (about 3 Hz) was similar as Rong’s simulation result. Compared with Bokkers’ simulated and experimental jetting bubble size, the more similar bubble size and solid velocity vectors around the bubble were obtained by the parallel algorithm. The solidexchange between two half beds in both forms of the first (~1 Hz) and second (>2 Hz) domain frequency was simulated, which was similar as the experimental result.
Key words:parallel; DEM model; two-phase flow; fluidized bed; numerical simulation
