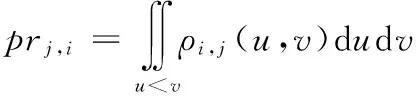基于不确定QoS的Web服务选择

沈梦婷　刘方方

(上海大学计算机工程与科学学院　上海 200444)



基于不确定QoS的Web服务选择

沈梦婷刘方方

(上海大学计算机工程与科学学院上海 200444)

摘要服务质量(QoS)是Web服务选择的一个重要考虑因素。目前基于QoS的Web服务选择研究多针对确定的QoS数据，此类方法不适合处理不确定的QoS属性。而已有的针对不确定QoS属性的研究方法基于离散的QoS属性，无法处理QoS属性连续时的情形。因此，提出针对不确定的连续QoS属性的查询方法，并提出QoS属性值在一定分布下的优化方法。实验表明，该方法能有效解决Web服务QoS属性连续条件下的查询，具备一定的可行性。

关键词Web服务不确定性QoS

0引言

Internet环境下Web服务通过WSDL、SOAP和UDDI等一组技术标准进行通信。随着Web服务技术的广泛应用，Internet上不同的服务商提供了功能相似的Web服务。如何利用不同的QoS属性值，从功能相似的Web服务中查找选择高质量、满足用户需求的服务，已成为热点研究问题之一。例如，通过公寓查询服务从不同的代理上获得一系列的价格、信誉、响应时间等租房信息，利用这些服务的QoS信息，选择一个最能满足用户需求的Web服务，或通过服务排序得到最好的几个服务。

目前对基于QoS的Web服务的研究多数是假定QoS属性是确定的，固定不变的。例如，查询公寓是一个单间需要998美元，这是一个固定不变的数。然而，有时价格并非是一个固定的值，可能是在一个区间里浮动，如表1所示，价格可在区间[＄990,＄1200]浮动。除了价格外，其他属性也会在区间里浮动，比如等候申请公寓的人数较多，导致批准时间可能在1到2个月内，公寓的声誉可能处在中等和高等之间等。以此可见，这些属性更适合用区间表示。

在实际应用中，用确定性的方法研究Web服务往往不适用于处理不确定QoS。例如，用户想根据价格对Web服务进行排序，而价格并非是一个确定离散的值。如表1所示，“pleasant view”的价格下界低于“sg.Court”的下界，它的上界高于后者的上界。此时QoS属性不是离散的，因而无法用加权平均值这种计算确定QoS的方法来解决Web服务排序问题。

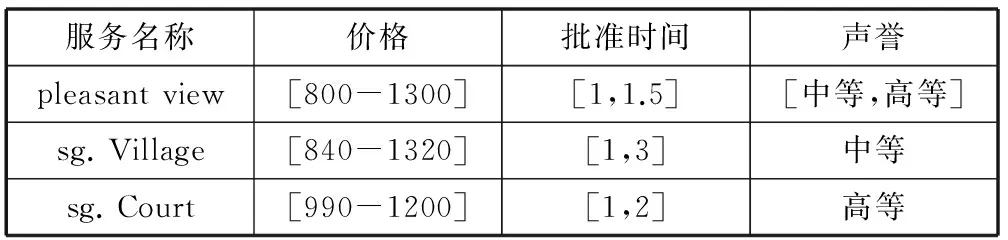
表1　租借服务

目前提出了不少针对不确定QoS的Web服务选择的方法，而这些方法主要是在QoS属性离散的情况下，即每个QoS值有一个存在概率。例如，响应时间1000 ms，它的存在概率是0.7。为了处理这类不确定数据，文献[1]提出了用属性的历史值来统计算不确定QoS值和存在概率的方法。而文献[2,14-17]利用skyline的方法查询相似服务之间QoS属性的支配关系，从而避免给QoS属性分配权重。这些方法只考虑了QoS属性是离散的，并没有考虑到QoS属性是区间值或连续的情况。

本文提出基于不确定连续QoS属性值的Web服务选择方法。目前，概率数据已经在数据库领域广泛地被研究[3-9]。对于连续性的不确定数据的研究则更具有挑战性。其中有两个原因:(1) 不确定数据的查询语义并没有统一的定义。比如，租借服务的某些提供者暂无房源时，查询结果是否还需要选择考虑这些服务。而在不确定数据研究中[3-9]，这些服务虽然不可用，但服务本身仍然存在，也是记录中的一部分。由此可见，语义不同，查询结果也会不同。(2) 对不确定数据的排序将涉及到高维概率计算，导致算法的时间消耗大。

本文针对实际应用场景，提出解决不确定QoS的Web服务查询方法，它将不确定数据的查询语义应用到服务查询中。本文给出两种查询定义：top-uncertain 和uncertain score rank。前一种方法和U-topk[5]类似，但是U-topk只考虑离散数据，而top-uncertain是基于连续数据。后一种方法类似U-kRank的连续分布的扩展[3,4]。最后，通过实验表明，本文提出的两种方法能有效解决Web服务QoS属性连续条件下的查询，具备一定的可行性。

1查询定义

由于Web服务处在开放的互联网环境中， QoS受多方面影响产生不确定性。目前处理这种不确定性主要几种在QoS离散的情况下，即计算每条记录的存在概率，并没考虑到QoS属性是区间值或连续的情况。至此，本节介绍Web服务中不确定连续QoS的表示，同时介绍两种针对QoS连续的情况下的查询定义。

本文定义的两种算法分别针对不同的应用场景，前者假定QoS记录存在概率为1，即不考虑服务的可信程度；后者则假设QoS记录有一个存在概率，主要适用于对可信度要求较高的应用场景。

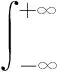
(1)其中pr(sj)表示Web服务sj的存在概率。式中，它由各个属性的存在概率决定。例如，由于受网络的影响，Web服务的响应时间会出现波动，同时服务被客户正确使用的概率，即可用性也会随着时间的变化不断改变。区间表示集中出现的波动范围，每个属性的浮动区间存在一个概率密度函数。一个Web服务的可信概率，也即存在概率，即所有属性存在概率累乘。式(1)可解决在不确定连续QoS属性下Web服务存在概率的计算。

多数情况下，用户喜欢通过计算QoS整体分值的方法找出满足他们要求的Web服务。因此，本文定义了score(sj;q1,…,qn)来描述QoS的整体分值，记为score(sj)。QoS值是由聚合函数得到的，假设聚合函数是线性函数，QoS的权重已经被分配(默认的或者用户定义)。这样，score(sj)计算如下：

(2)

式(2)是一个聚合函数，通过聚合函数，将多个属性聚合按照一定规则聚合成一个QoS值，用这种化多为少的方法可解决多目标决策问题。同时，计算中融入用户需求和偏好计算的QoS值，更能准确地选择满足用户需求的服务。

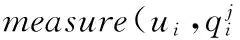
在文献[4]中，为了计算的简化，认为sj的存在概率为1，即sj的存在和它的属性存在不相关；而另一种情况， 假定sj的存在概率是QoS值的存在概率。对于由连续不确定QoS属性值计算得到的QoS值来说，每个记录的QoS值也是连续不确定的，把它作为服务的一个特殊属性值。此时，pr(sj)用pr(score(sj))表示。

在Web服务的中，以上两种情况都有可能发生。所以，本文定义这两种情况下的查询语义。

例1假设表1中的QoS属性的线性聚合函数为score(sj)=0.3·mprice+0.4·mw_l+0.3·mreputation。用户想根据QoS值排名得到前二个的服务。由于 “sg.Court” 暂无房源，针对不同的查询语义将得到不同的结果。例如，如果考虑所有服务都存在，返回的结果为{s1,s3}，而只考虑有房源的服务，则返回的结果为{s1,s2}。

针对第一种情况，以QoS记录的存在概率为1为前提，这样，返回结果排名只取决于QoS值的分布。本文对其做如下定义：

定义1Top-uncertain QoS:S={sj}是一组服务集，T={T1,…,Tm}， 是一组长度为k的服务向量集，每个Ti集中的服务都是根据QoS值进行排序。Top-uncertain QoS的返回结果记为T*，其中T*=argmaxT*∈T (∑sj∈T*pr(score(sj)))。

定义1和u-topk[5]相似，都是返回元组集中概率最大的K个服务。不同的是，u-topk所返回的是所有可能世界中发生概率最大的。而本文以服务的存在概率为1为前提，针对不确定的连续QoS属性提出的一种查询方法。

第二种情况，服务记录是否存在由QoS值的存在概率决定。其中，QoS值的概率分布即是存在概率分布。在这种情况下，和Top-uncertain QoS的返回结果不同，因为对服务的排序不仅由QoS值也由它存在概率决定。例如，表1中有三个service，假设它们的存在概率不是1，由这三个服务组成的可能世界[5-7]有{s1},{s2},{s3},{s1,s2},{s2,s3},{s1,s3},{s1,s2,s3}。以服务s3为例，在不同的可能世界实例中，它的排序位置不同。

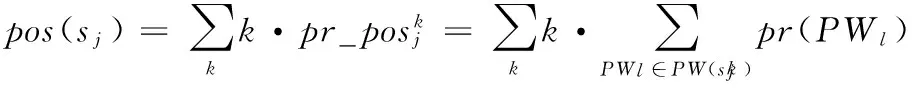
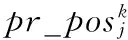
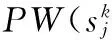
pr(PWl)是PWl的存在概率。它为其包含服务S的存在概率的累积。

此方法根据计算的位置函数值返回最优的K个服务。定义2类似于U-kRank[3,8,9]，都是通过计算可能世界中的位置排名返回最优的K个服务，不同之处定义2所计算的QoS值的概率作为记录的存在的概率。

2查询算法

对不确定数据进行排序和查询选择时需要考虑其概率和各属性值之间组成的语义，文献[5]提出了结合可信值和数据值的查询算法U-topk和U-kRank。这两种算法都是在数据概率离散情况下的处理方式，而对数据连续分布的情况未作出处理。本节提出的两种查询算法top-uncertain QoS和uncertain score rank，旨在解决不确定连续QoS的Web服务选择。

不同的查询语义所强调的是其所满足的性质和应用环境。本文提出的两种适用不同的应用环境的查询语义算法。

2.1top-uncertain QoS计算

本方法中，假设QoS记录存在概率为1。本文重点是通过QoS值的概率密度分布进行比较。QoS属性值是不确定连续，而对于QoS值来说，每个记录的QoS值也是连续不确定的，此时，服务的排序是由区间和概率密度分布决定的。当记录相互独立，QoS值具有相同概率密度分布时，通过比较积分面积[4]去比较哪个服务具有更高的服务质量的概率。具体如下：

首先，比较si和sj。si和sj的区间分别由[li,ui]和[lj,uj]表示。QoS值也有相同的概率分布。设概率密度函数为ρ。这样得到：

假设sj也有相同的概率分布，当si和sj都是连续区间上的变量时，si的QoS值大于sj的概率为：

式中，ρi,j为si和sj的QoS值变量的联合概率密度函数。Di,j表示u>v的积分域,即score(si)>score(sj)。

如图1所示，x坐标和y坐标分别表示si和sj的区间。si和sj区间组成的面积被直线y=x分割成ai和aj两个部分。如果ai>aj,则si的QoS值大于sj的QoS值可能性高，即pr(score(si)>score(sj))>pr(score(si)≤score(sj))。

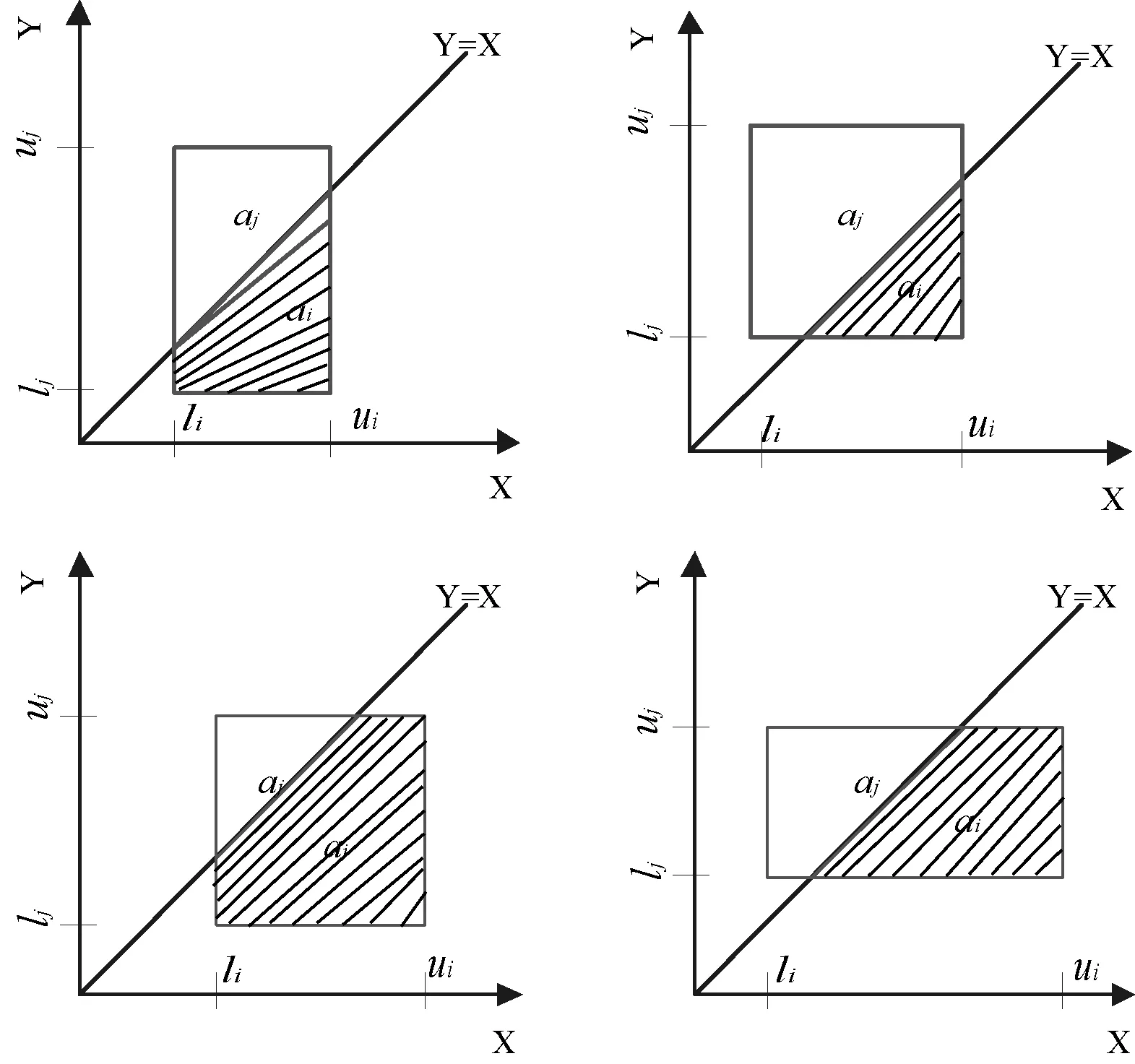
图1　积分面积不同的情况

当记录存在概率为1，QoS值符合相同密度分布时，top-uncertain QoS通过比较积分面积[4]计算两服务之间具有更高的服务质量的概率，从而避免多重积分的计算，降低时间消耗。它不考虑记录可信度，即假设记录的存在概率为1。例如，在公寓查询时，它没有考虑无房源的情况。

下面是top-uncertain QoS的算法：

其中，comp(si,sj)表示比较哪个服务具有更高的服务质量，如果si>sj，则comp(si,sj)=1；否则为0。DS表示服务集；ret_serk代表服务返回的k个结果，当DS为空时算法终止。Queue存储被访问的、不在ret_serk里的服务集。

算法1top-uncertain QoS算法

1:初始化：Queue←φ，ret_ser0←φ

d←0表示查询深度

2:ret_serk←DS中最先出栈k个

3:high,low←ret_serk中最大最小的代表值

4:while (DS≠φ) do

5:sd←DS中当前出栈的服务

6:if comp(high,sd)=0

7:if comp(sd,low)=1

8:ret_serk←sd

9:low←ret_serk中最小的代表值

10:else

11:Queue←sd

12:else

13:ret_serk←sd

14:high←sd

15:endif

16:endwhile

17:return ret_serk

2.2uncertain score rank计算

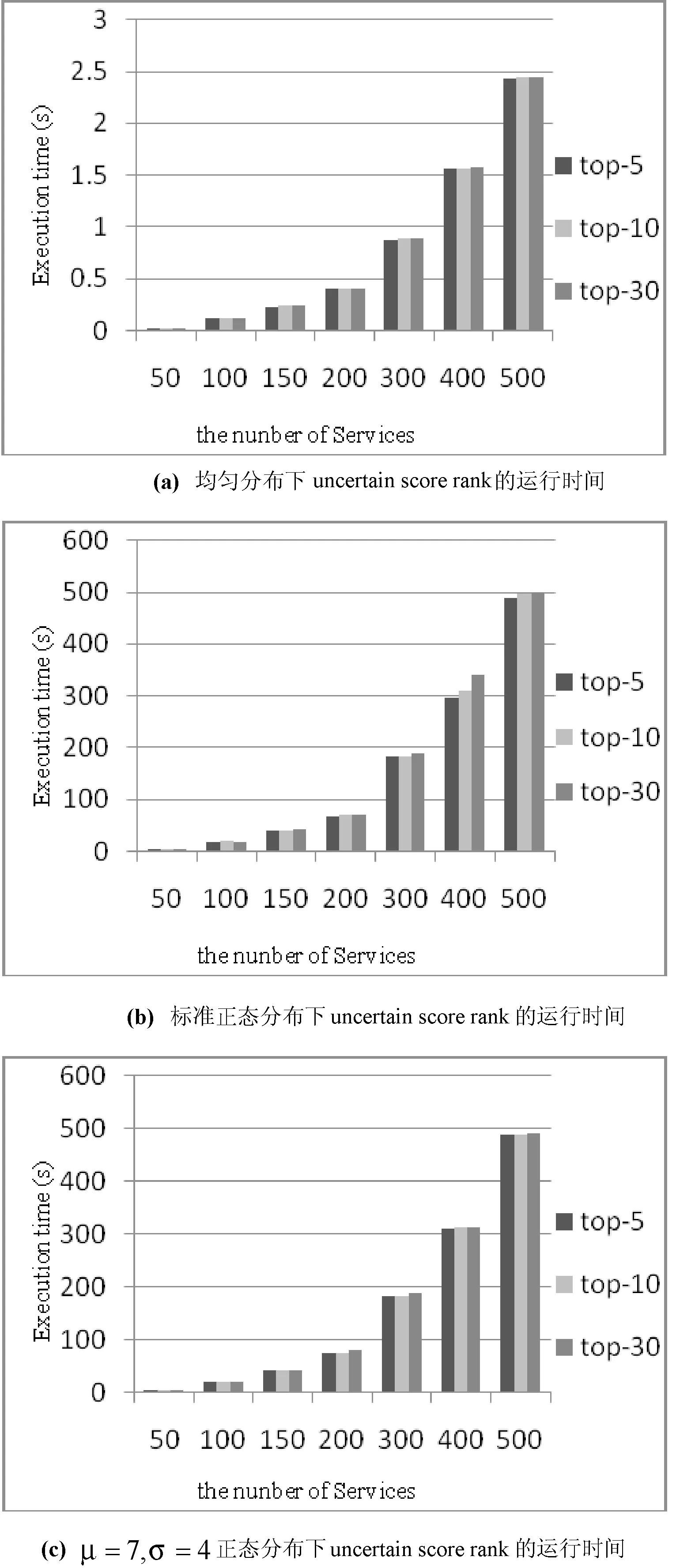
在计算top-uncertain QoS时，如果QoS记录存在概率不等于1。根据该定义，需要扫描所有的可能世界。例如表1,3个服务产生7个可能世界。通常情况下，n个服务将产生2n个可能世界。由此可见，随着服务数量的增加，可能世界会成指数级增加，这样大大增加了计算的时间复杂度。

文献[3]提出了一种剪枝的算法以减少运算代价。这种PRF方法基于离散不确定数据，当QoS值是离散的时候，递减排序。对于服务si，{sj}i集表示QoS值高于si的集合。由于低于si的QoS值的服务不会对si的排名结果造成影响，所以{sj}i只考虑QoS值高于si的集合。文献[8,9]提出了多项式系数的方法求解si排名k的所有可能世界的概率累和。其多项式公式如下：

(3)

将多项式展开如下：

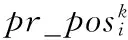
式(3)只考虑离散的不确定数据条件下，本文将它扩展应用到不确定的连续数据，uncertain score rank是利用PRF多项式系数得到服务排名位置的概率。然后计算返回pos(si)值最好的前K个。

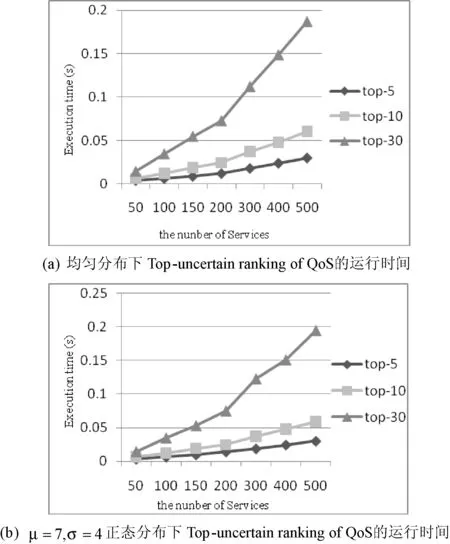
综上，当pr(sj)为pr(score(sj))时式(3)转换为：

pr(score(sj)>score(si))x)

(1-pr(score(sj)≤score(si))x)

(4)

用变量v替换score(si)式(4)变为如下：

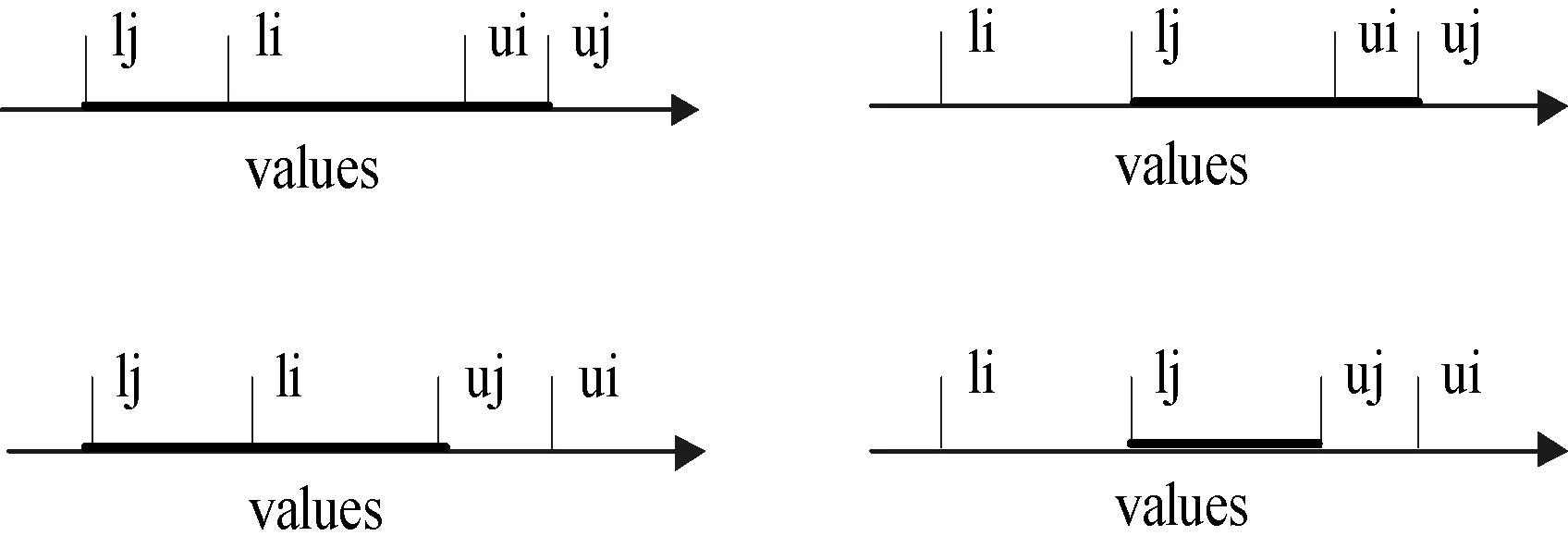
pr(score(sj)

整理得：

(5)

其中，ρi,j(u,v)是si和sj的QoS值的联合概率密度函数。

得出：

化简得：

(6)

其中，n是服务的总数。

用式(6)，可计算每个服务的pos(si)。最后返回pos值高的前k个。

Uncertain score rank算法考虑了记录可信度。假定记录的存在概率为QoS值的存在概率，对于由连续不确定QoS属性计算得到的QoS值来说，每个记录的QoS值也是连续不确定的，这种算法适用于对可信度要求较高的服务选择情况。例如，在公寓查询时，将无房源的情况考虑进去。

3实验结果分析

目前互联网的Web服务数量不超过10 000个，功能相同的服务也不超过300个，因此我们选择Web服务数量的范围在50到500之间。为验证uncertain score rank和 top-uncertain ranking of QoS这两种算法的可行性。本文模拟一个数据集，每个数据集有500条数据。每条记录的上下界在[0,10]中间浮动，记录的区间大小从0到10不等。本文假设概率分布分别符合均匀分布、标准正态分布和自定义正态分布的三种情况出发分析两种方法的执行时间。

在Web服务中，受到开放性网络的影响，其服务的响应时间集中在一定范围内浮动，离散的数据未能正确反映原有数据的分布。同时如按照离散型QoS属性值处理，当样本数据量庞大，很难准确计算每条记录的概率，如用简单的概率分布函数表示存在概率，可避免每条记录的概率计算。通过本实验分析表明，该方法能有效解决Web服务QoS属性连续条件下的查询，具备一定的可行性。

3.1基于均匀分布和正态分布的uncertain score rank

利用式(6)，通过计算每个sj的prj,i来计算si的位置QoS值，si和sj无论属于哪种概率分布。当ui

图2　服务QoS属性值区间

根据上述的4中情况，prj,i的计算如下：

(7)

根据式(6)、式(7)，可计算服务的位置QoS值。

在服务数量不同，返回服务个数不同的情况下，图3分别表示均匀分布和正态分布条件下uncertain score rank的运行时间。

图3　uncertain score rank运行时间

在正态分布的情况下，si的概率密度函数为：

图3(b)和图3(c)分别是标准正态分布和μ=7,σ=4的正态分布图。运行时间随着服务数量的增加而增加，而k值的变化对运行时间的影响并不大。

从图3得出，对于不同的分布，时间消耗主要在可能性pr的计算上。

3.2基于均匀分布和正态分布的Top-uncertain ranking of QoS

这种方法，我们不需要计算位置的多重积分值，只需要比较服务si和sj的QoS属性值区间所围成的面积大小。而且不需知道其服务属于哪种分布，即不同分布对此方法的时间消耗没有影响。

图4是不同的服务数量在两种不同分布下的运行时间。

图4　Top-uncertain ranking of QoS运行时间

4相关工作

随着功能相似的Web服务的逐渐增多，基于QoS的Web服务选择已经成为目前的一个研究热点。

文献[8]提出了一种可扩展的QoS计算模型，它是根据用户反馈信息建立QoS信息的计算模型。文献[9,10]提出了利用线性规划的方法找到最佳服务。类似于这个方法，文献[11]提出了带有本地约束的线性编程模型。文献[12]研究了在多个QoS约束条件下的服务选择问题,它提出了两种QoS组合中的融入启发式算法的模型：(1) 组合模型；(2) 图模型。文献[13]介绍了一种用于评估多维属性的QoS的选择算法。以上的这些方法都是基于确定的QoS。

目前，也有不少针对不确定的QoS研究，文献[1]介绍了离散的不确定QoS属性，提出了一种对不确定QoS的描述方法，并给每个QoS属性设立一个权值，计算出Web服务中每条记录的加权QoS值之和进行排序。利用U检验或者峰度和偏态返回数值较小的Web服务。文献[2,14-17]提出了Skyline的QoS查询方法，这种方法不需要用户给出QoS的权重。文献[2,17]将Skyline的查询方法应用到了不确定QoS中，并提出了一种提高Skyline查询的效率方法。然而这些方法都是基于离散的不确定QoS。

连续的不确定性在文献[3,4]中被提出来，它比离散的不确定性更加复杂。对于连续的不确定数据的查询方法主要难点还是在查询语义的定义[4]和不确定数据的表示[3]。

针对不确定数据查询有不同的查询语义[5]，这些方法都是基于离散的数据。本文在现有的基础上，提出了基于连续不确定QoS的Web服务查询方法。最后通过实验验证了本文方法的可行性。

5结语

本文根据不同的查询语义，提出针对不确定的连续QoS属性的查询方法，并提出了QoS属性值在一定分布下的优化方法。实验表明，该方法能有效解决Web服务QoS属性连续条件下的查询，具备一定的可行性。接下去的工作主要集中以下两点：(1) 讨论涵盖更多应用场景的查询语义和研究相应的算法；(2) 研究如何优化技术，降低算法的复杂性，减少时间消耗。

参考文献

[1] Cheng Wan,Hongbing Wang.Uncertainty-aware QoS Description and Selection Model for Web Services[C]//IEEE International Conference on Services Computing,Salt Lake City,UT:IEEE,2007.

[2] Karim Benouare,Djamal Benslimane,Allel Hadjali.Selecting Skyline Web Services from Uncertain QoS[C]//IEEE International Conference on Services Computing, HI:IEEE,2012.

[3] Jian Li,Amol Deshpande.Ranking Continuous Probabilistic Datasets[J].Proceedings of the VLDB Endowment,2010,3(1):638-649.

[4] Chonghai Wang,Liyan Yuan,Jiahuai You.On the semantics of top-k ranking for objects with uncertain data[J].Computers and Mathematics with Applications,2011,62(7):2812-2823.

[5] Soliman M,Ilyas I,Chang K C.Top-k query processing in uncertain databases[C]//IEEE 23rdInternational Conference on Data Engineering,Istanbul:IEEE,2007.

[6] Chonghai Wang,Li Yan Yuan,Jia Huai You,et al.On Pruning for Top K Ranking in Uncertain Databases[J].PVLDB,2011,4(10):598-609.

[7] Gupta R,Sarawagi S.Creating Probabilistic Databases from Informaiton Extraction Model[C]//Proceedings of the 32nd international conference on Very large data bases,2006.

[8] Jian Li,Barna Saha,Amol Deshpande.A Unified Approach to Raning in Probabilistic Databases[J].The VLDB Journal,2009,20(2):249-275.

[9] Jian Li,Amol Deshpande.Consensus answers for queries over probabilistic databases[C]//Proceedings of the twenty-eighth ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems,New York:ACM,2009.

[10] Liu Y,Ngu A H H,Zeng L.Qos computation and policing in dynamic web service selection[C]//Proceedings of the 13th international World Wide Web conference on Alternate track papers & posters,New York:ACM,2004.

[11] Zeng L,Benatallah B,Dumas M,et al.Quality driven web services composition[C]//Quality driven web services composition,New York:ACM,2003.

[12] Zeng L,Benatallah B,Ngu A H H,et al.Qos-aware middleware for web services composition[J].IEEE Trans. Software Eng,2004,30(5):311-327.

[13] Ardagna D,Pernici B.Adaptive service composition in flexible processes[J].IEEE Trans.Software Eng,2007,33(6):369-384.

[14] Yu T,Zhang Y,Lin K J.Efficient algorithms for web services selection with end-to-end qos constraints[J].ACM Transactions on the Web (TWEB),2007,1(1):1-26.

[15] Wang X,Vitvar T,Kerrigan M,et al.A qos-aware selection model for semantic web services[C]//Proceedings of the 4th international conference on Service-Oriented Computing,Berlin,Springer-Verlag,2006.

[16] Alrifai M,Skoutas D,Risse T.Selecting skyline services for qos-based web service composition[C]//Proceedings of the 19th international conference on World wide web,New York:ACM,2010.

[17] Yu Q,Bouguettaya A.Computing service skylines over sets of services[C]//2010 IEEE International Conference on Web Services,Miami,FL:IEEE,2010.

[18] Benouaret K,Benslimane B,HadjAli A.On the use of fuzzy dominance for computing service skyline based on qos[C]//2010 IEEE International Conference on Web Services, Washington,DC:IEEE,2011.

[19] Yu Q,Bouguettaya A.Computing service skyline from uncertain qows[J].IEEE T. Services Computing,2010,3(1):16-29.

收稿日期：2014-12-28。上海市自然科学基金项目(12ZR14110 00)；2015年度上海大学电影高峰学科成果。沈梦婷，硕士生，主研领域：Web service。刘方方，副教授。

中图分类号TP3

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.006

UNCERTAIN QOS-BASED WEB SERVICES SELECTION

Shen MengtingLiu Fangfang

(SchoolofComputerEngineeringandScience,ShanghaiUniversity,Shanghai200444,China)

AbstractQuality of service (QoS) is considered as a significant criterion for Web services selection. Most of researches in regard to QoS-based Web services selection focus on the determined QoS data, such kind of means are not suitable for processing uncertain QoS attributes. However existing research means for uncertain QoS attributes are based on discrete QoS attributes and cannot deal with the situation when the QoS attributes are in continuity. Therefore in this paper, we present the query method for continuous QoS attributes with uncertainty, and propose the optimisation approach for QoS attributes under certain distribution. It is indicated by experiment that the method is able to effectively solve the query of Web services under the condition of QoS attributes in continuity, and it possesses certain feasibility as well.

KeywordsWeb serviceUncertaintyQoS