浅析引力半径和轨道半径的异同
2016-08-04匡海发
匡海发


摘 要:《万有引力与航天》这章的特点是公式多、模型多,学生很难区分引力半径和轨道半径。笔者通过万有引力这章常见的3种模型来对引力半径和轨道半径加以区分。
关键词:万有引力;引力半径;轨道半径
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2016)7-0064-2
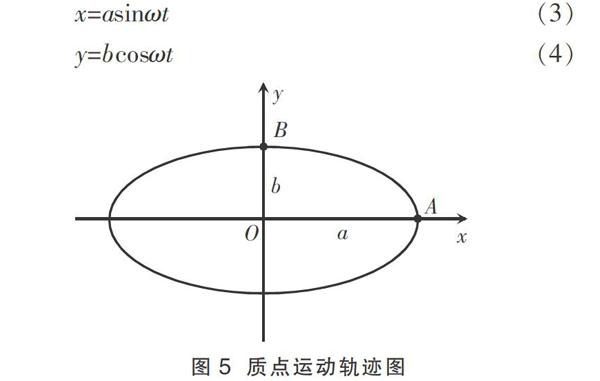
笔者在讲解卫星变轨问题时,学生提出:我们根据万有引力F=G和牛顿第二定律F=ma可以推出a=G(如图1)。在A点:r=r,所以,a=a。但是,卫星要从轨道1变为轨道2,卫星必须在A点进行一次瞬间加速,所以v 1 “中心天体+环绕天体”模型 如图2所示,M为中心天体的质量,R为中心天体的星球半径,m为环绕天体的质量,r为环绕天体的轨道半径,周期为T,根据圆周运动知识则有:G=mr。 引力半径指计算任何两个质点之间万有引力时,质点与质点之间的距离,用r表示。轨道半径指物体做圆周运动时,物体到圆心之间的距离,用r表示。根据定义可知,在“中心天体+环绕天体”模型中,引力半径r和轨道半径r相同。 2 双星天体模型 如图3所示,两颗星体质量分别为M、m,它们之间的距离为L,现它们绕O点做匀速圆周运动,轨道半径分别为rM、rm,角速度为ω,则根据圆周运动知识有: M:G=Mω2rM(1) m:G=Mω2rm(2) (1)和(2)式中,引力半径是L,M和m的轨道半径分别为rM、rm,可以看出引力半径和轨道半径在双星系统中是不同的。 3 卫星变轨模型 如图4所示,轨道1是近圆轨道(停泊轨道),轨道2是椭圆轨道(转移轨道),轨道3是远地圆轨道(预设轨道),如卫星要从轨道1变为轨道2,需要在图4中的A位置瞬间加速,所以v 首先,要分析曲线运动的质点在曲线上某点的运动情况,往往先要弄清楚曲线在这一点的切线方向及程度。切线方向可由切线的斜率反映出来,弯曲程度可用极限圆曲率半径反映出来。如果在曲线上某点附近取一段,只要取得足够短,那么,这一小段就可以看成一段很短的圆弧,此圆弧所在的圆叫做曲线在该点的极限圆,极限圆的半径叫曲线在该点的曲率半径(符号ρ)。 下面讨论椭圆在A和B点的曲率半径: 假设质点的运动轨迹方程为:+=1,如图5所示,把质点的椭圆运动看成两个相互垂直的同频率简谐振动的叠加,即: 根据公式an=计算向心加速度时,笔者认为r应指的是该点的曲率半径(即轨道半径),即使卫星从轨道1变为轨道2,在近地点有瞬间加速。但是,最后通过两种方式计算出来加速度,也得出相同的结论:。 笔者认为在讲解《万有引力与航天》这章内容时,如果能抓住本章的一个中心(万有引力提供向心为中心)、两个半径(引力半径和轨道半径)、多种变化(公式变形)进行教学,也许会收到事半功倍的效果。 参考文献: [1]温黎明.椭圆曲率半径的四种求法[J].中学生数理化·教与学,2009(12):121—122.(栏目编辑 邓 磊)
