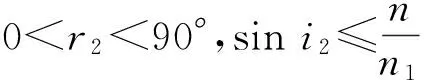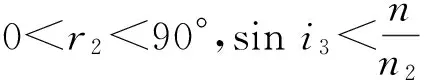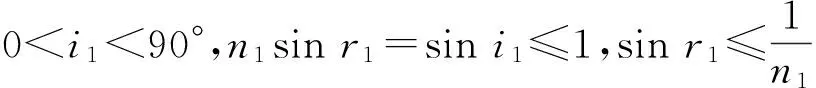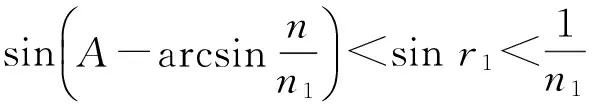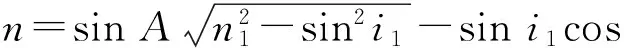用双棱镜测量液体的折射率

苏为宁，周　进，周慧君

(南京大学 物理实验教学中心，江苏 南京 210093)



用双棱镜测量液体的折射率

苏为宁，周进，周慧君

(南京大学 物理实验教学中心，江苏 南京 210093)

摘要：根据光在三棱镜中的色散关系和界面全反射，测量了液体的色散曲线和折射率. 该题目作为全国大学生物理竞赛的基础实验试题，考察了学生的理论知识和动手能力.

关键词：折射率；色散；三棱镜；分光计

作为“第3届全国大学生物理竞赛”的基础题，首先在大学物理实验教学大纲[1]的要求下，考核学生对基本仪器的使用情况，在此基础上，要求学生根据具体的测量项目，灵活使用实验中提供的仪器，设计实验方案，并测量要求的参量,考察学生的动手能力，以及运用现有的理论知识和实验仪器解决实际问题的能力. “液体的色散曲线的测量”是一个基础实验题目，首先考核学生应用分光计测量棱镜的顶角和色散率，在此基础上，拓展测量内容，要求学生应用2快形状相同、折射率不同的棱镜，测量液体的色散关系.

1试题

试题题目：液体的色散曲线的测量.

每人1套仪器，考试时间为4 h.

基础知识：光在异质界面上折射，如果入射方折射率为n1，入射角为i,出射方折射率为n2，折射角为r,那么：n1sini=n2sinr. 光经过三棱镜(图1)，入射角为i1，出射角为r2，出射光偏离入射方向的角度称为偏向角，偏向角的大小随入射角的变化而变化，通常可以测出三棱镜的顶角A和最小偏向角δ[2]，由此算出三棱镜的折射率，即

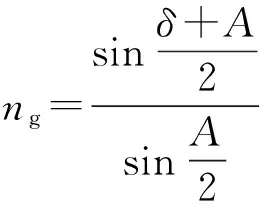
待研究问题：在2块尺寸相同的三棱镜间夹1层液体膜，根据出射光谱，测量液体的折射率.

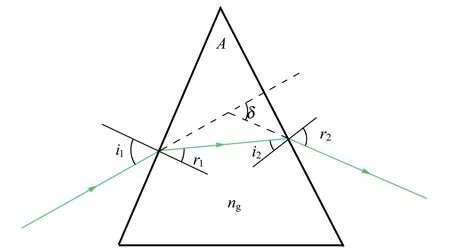
图1　光在三棱镜中散射的光路图

实验器具：分光计，2块顶角近似相同折射率不同的等腰三棱镜A和B，高压汞灯，水平仪，平面镜，待测液体，容器，滴管，垫分光计脚的纸片.

实验要求：所有数据只要求单次测量.

1)判断A和B哪个棱镜的折射率高？

2)测量折射率低的三棱镜的顶角.

a.画出测量光路图.

b.测出顶角.

3)测量较低折射率棱镜的色散曲线n-λ(要求至少测量5个点，并作图) .

a.写出实验主要步骤并测量.

b.作出色散曲线.

4)测量给定液体的色散曲线，这一部分可索要求助方案(包括实验光路图、测量公式).

a.画出实验光路图.

b.导出所需要的公式.

c.作出液体的色散曲线.

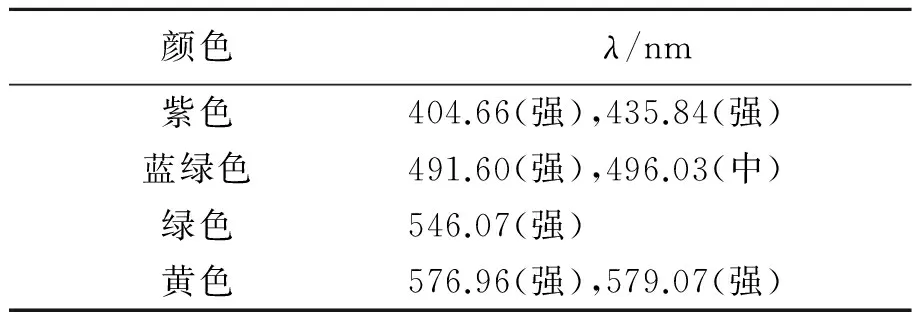
表1　汞灯的主要谱线波长

2试题解答

1)折射率高，偏向角大，出射光谱散得开，由此很容易选出折射率高的棱镜.

2)测量三棱镜的顶角，可分别测量三棱镜2个光学面的法线1和2的角位置(图2)，由此算出顶角A.

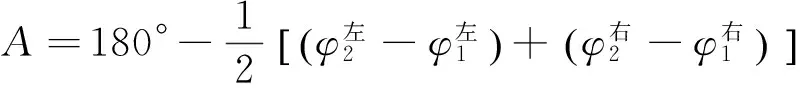
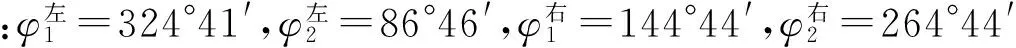
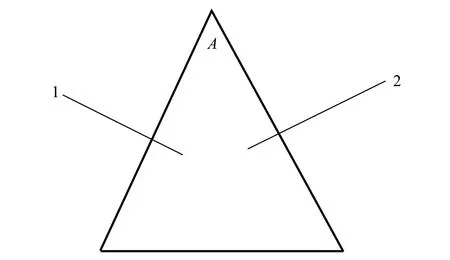
图2　测量三棱镜的顶角的示意图

3)跟踪待测的光谱，改变入射角(旋转内盘)寻找最小偏转角位置，然后锁定内盘，测量出射光谱θi和白光θ0的位置，由此算出待测光谱的最小偏向角δ. 对每一种颜色的光谱，都要寻找最小偏向角位置，然后再测量. 测量结果见表2，色散曲线见图3.

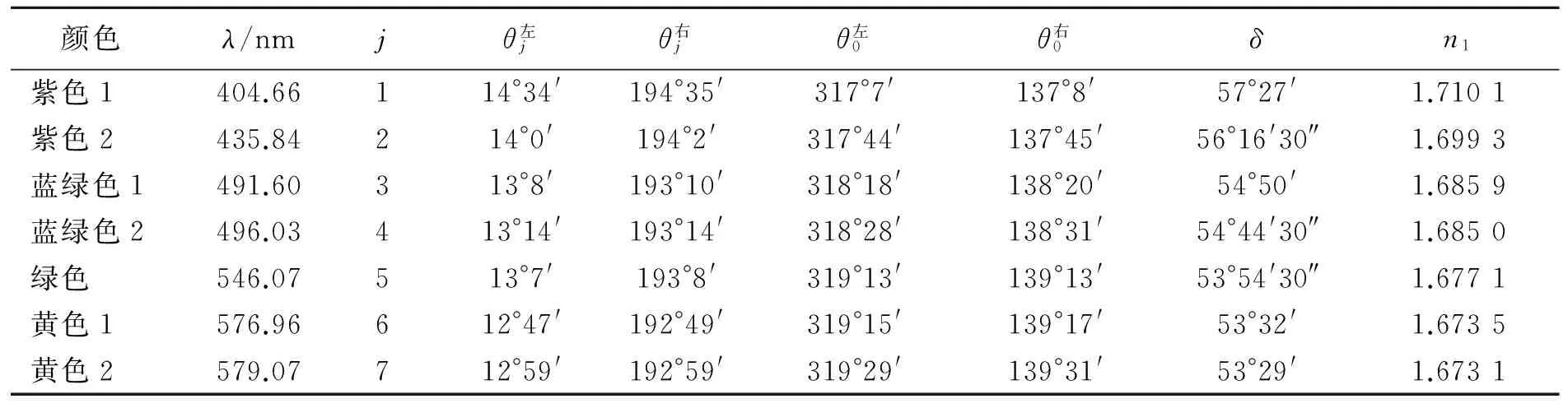
表2　测量棱镜A的最小偏向角δ和折射率n1

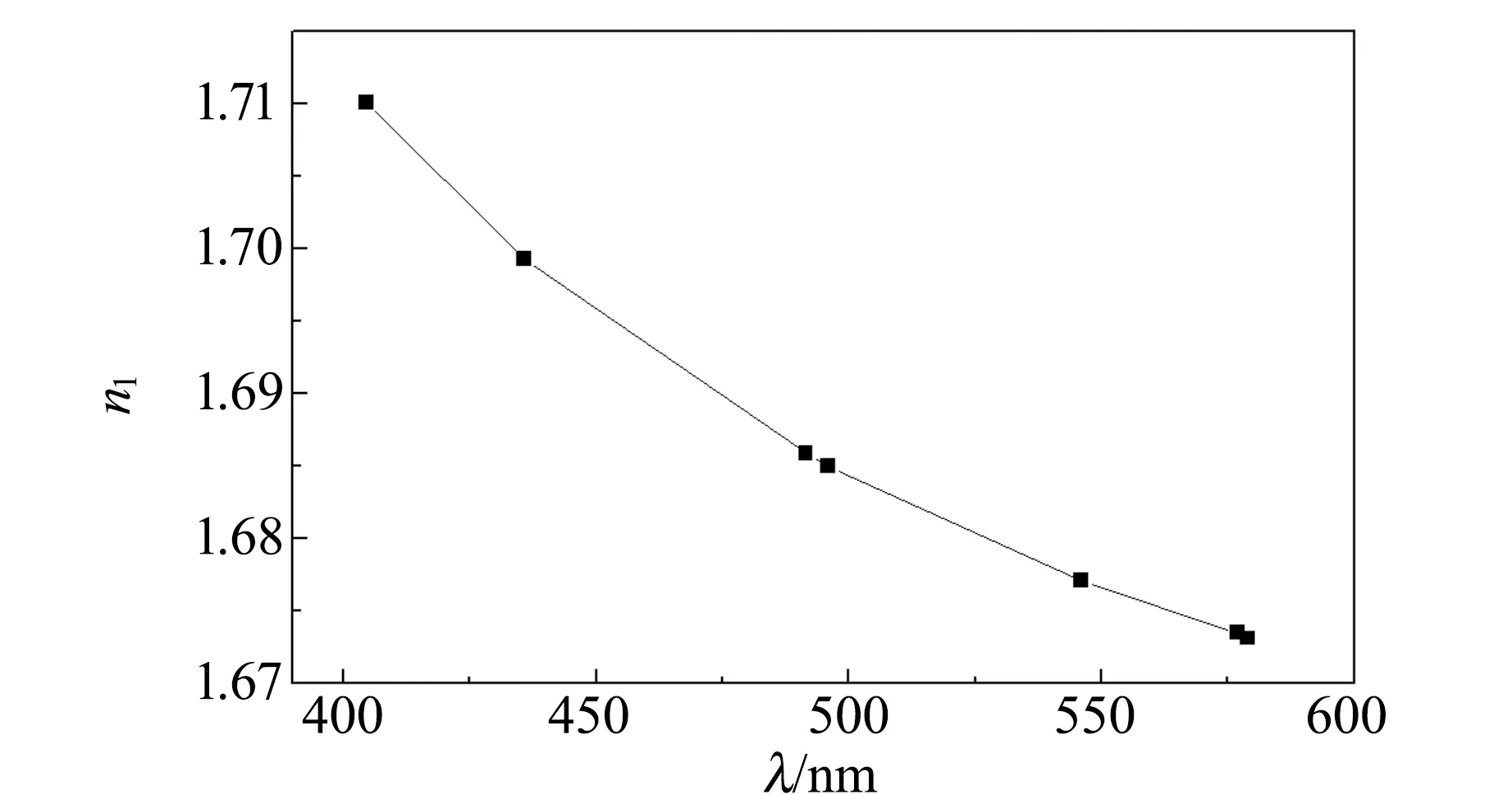
图3　三棱镜的色散曲线

4)测量液体的色散曲线

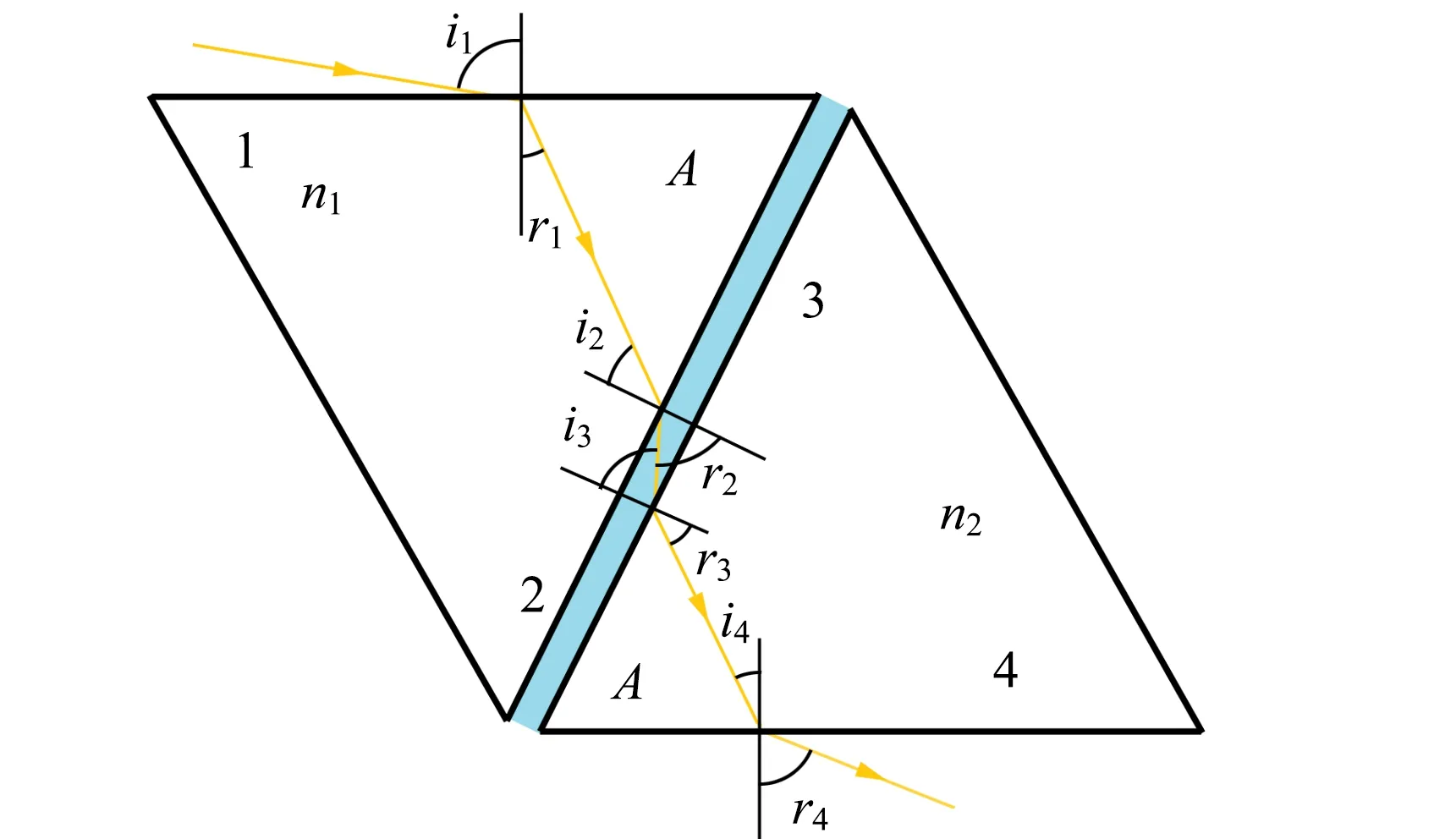
用2块三棱镜制备液膜，并且测量液膜的折射率，光路图见图4[3-4].

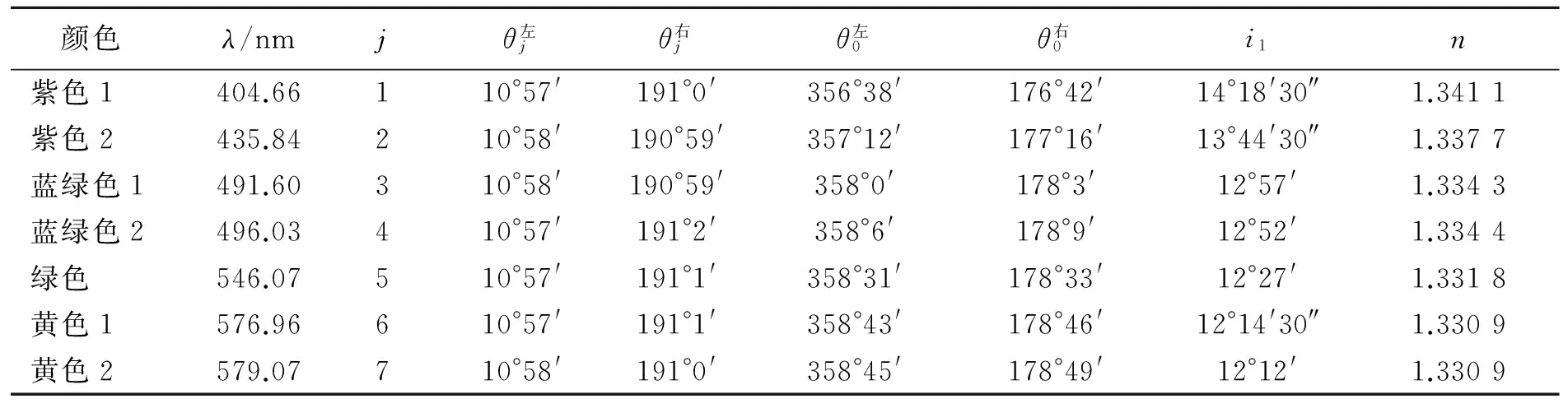
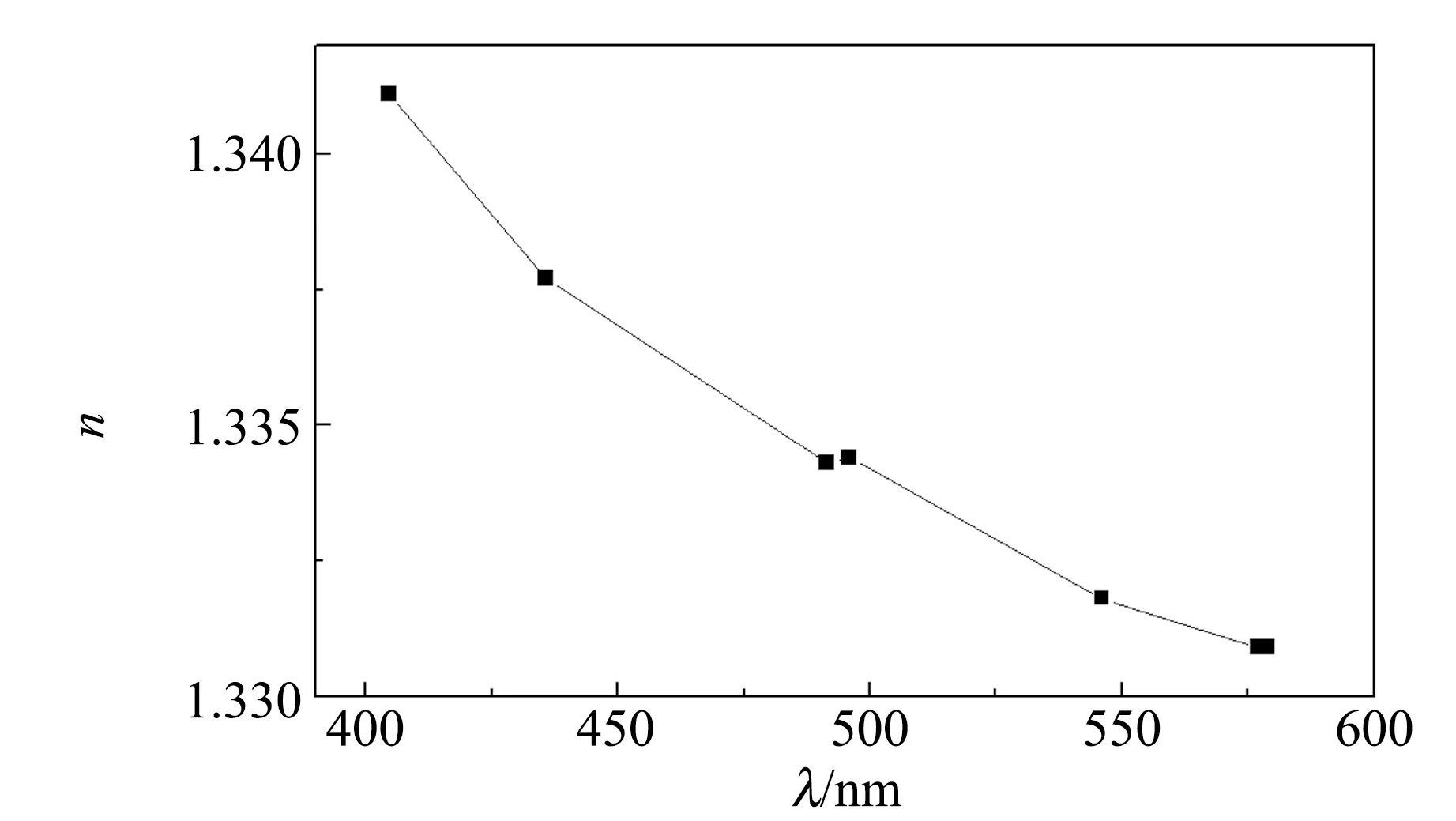
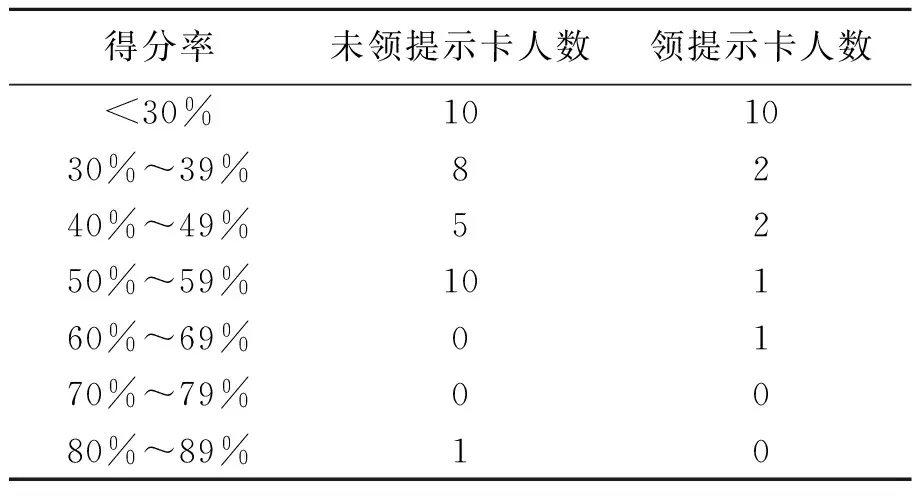
设空气的折射率为1，三棱镜的折射率分别为n1和n2,顶角为A，待测液体的折射率为n，且满足关系：n

图4　测量液体的色散曲线的光路图

光线在界面 1上的入射角为i1，折射角为r1，入射角的可能范围为0

sini1=n1sinr1≤1,

n1sini2=nsinr2≤n,

(1)

i2=A-r1.

可能通过界面2的光线，满足：

(2)

那么

(3)

光线经过液体膜以后，在界面3上入射，入射角i3=r2，

nsini3=n2sinr3.

(4)

光线到达界面 4时，入射角为i4，折射角为r4. 可观察到出射光谱时，折射角的范围是0

n2sini4=sinr4≤1.

(5)

根据光路可逆，在界面3上，只有满足关系：

(6)

界面1上，光线也要满足关系：

(7)

综合(3)和(7)式得

(8)

当在界面 2 折返的光线满足r2=90°，则：

(9)

实验用汞灯作光源，在光学面 4 一侧可观测到分立的光谱，改变入射角(转动内盘)，可看到光谱线从紫光开始逐条消失，跟踪光谱线消失那一刻(锁定内盘)，测量入射光的位置及光学面 1 (或光学面 4 )的法线方向，求出入射角i1，代入式(9)，即可算出待测液体的折射率. 测量结果见表3，色散曲线见图5.

表3　测量入射角i1和液体折射率n

图5　液体的色散曲线

3考试结果及评析

第一小题“判断哪个棱镜折射率高”，考察考生对偏向角与折射率关系的理解；第二小题“测量三棱镜的顶角”，考察了考生对仪器的了解程度；第三小题“测量三棱镜的色散曲线”，是实验大纲要求的内容，这3个问题难度不大，实验内容和数据处理量适中，而且都是大学物理实验必做的实验项目. 第四小题“测量液体的色散曲线”，包含了3个小问题，其中的前2个小问可以借助“求助方案”得到实验光路图和测量公式，代价是总分扣20分，这一小题建立在前面三题的基础上，对考生的理论知识和实验动手能力都有较高的要求. 共有50人参加考试，其中34人未申请提示卡，16人陆续申请了提示卡. 从实验过程和答卷结果看，在提供仪器说明书的前提下，还是有少数考生不会使用分光计. 前面3小题属于大纲的教学内容，这部分考题占总分的60%，有一半的考生可以得到其中50%的分数；第4小题超出大纲要求，考察学生综合应用分光计及理论联系实际的能力. 这部分考题占总分的40%,领到提示卡的考生，在实验测量和回答问题时，目的性比较明确，但扣掉提示卡的20分以后，得分率也不高. 表4是考生总得分的情况统计，以及扣除提示卡的20分以后，两部分考生的卷面总分得的统计情况比较.

表4　扣掉求助的20分以后总得分的情况统计

考试结果表明：大部分考生分析问题、解决问题的能力较弱，其中有相当一部分考生对基本的实验仪器不了解，动手能力差，这警示在以后的大学物理实验教学过程中，要加强仪器功能的说明，强化仪器使用的训练，最重要的是增加了学生的自主实验方面的训练，切实提高了学生的综合实验能力.

参考文献：

[1]教育部高等学校物理学与天文学教学指导委员会，物理基础课程教学指导分委员会. 理工科类大学物理实验课程教学基本要求[M]. 北京：高等教育出版社，2012.

[2]胡小鹏，高文莉，万春华. 大学物理实验(第一册)[M]. 南京:南京大学出版社，2011.

[3]张蕾,赵锦柱，王思慧，等. 棱镜法测量水的色散[J]. 物理与工程,2007,17(2)：46-48.

[4]贺昊，赵地，王鑫，等. 布儒斯特角法测金属薄膜折射率并解释不消光现象[J]. 物理实验,2013,33(6)：40-43.

[责任编辑：任德香]

收稿日期：2016-04-05

作者简介：苏为宁(1963-)，女，浙江玉环人，南京大学物理系教授，硕士，从事基础物理教学与研究.

中图分类号：O43

文献标识码：A

文章编号：1005-4642(2016)07-0028-04

Measuring the refractive index of liquid with double prism

SU Wei-ning, ZHOU Jin， ZHOU Hui-jun

(Physics Experiment Center, Nanjing University, Nanjing 210093, China)

Abstract:The dispersion curve and refractive index of the liquid were measured according the dispersion relation of prism and the total reflection at the interface. As the basis test question of the experiment exam of the national college students’ physics competition, the students’ theoretical knowledge and practical ability were tested.

Key words:refractive index; dispersion; prism; spectrometer