基于Q函数优化的加权有向复杂网络模糊聚类算法设计研究

李海威，韦天瀚

（1.广东省财政数据信息中心，广东广州　510030；2.香港中文大学，香港）

基于Q函数优化的加权有向复杂网络模糊聚类算法设计研究

李海威1，韦天瀚2

（1.广东省财政数据信息中心，广东广州510030；2.香港中文大学，香港）

研究加权有向复杂网络中社团的模糊聚类算法，在谱平分、FCM算法的基础上，构建新的适用于加权有向复杂网络模糊划分的Q函数，设计了复杂网络模糊聚类算法，并针对FCM聚类算法结果不稳定的现象进行了算法上的改进，使算法更适合于现实世界。通过实验数据验证了设计的算法，从总体上提高算法的划分精确度，结果也趋向于稳定。解决了从加权有向复杂网络、模糊集中发现、划分社团的实际问题。

复杂网络；FCM算法；Q函数优化；谱平分

0引言

许多研究表明，真实世界的大量网络都具有社团结构的特征，复杂网络的社团结构对实际系统有着重要的含义：在社会网络中，不同的社团结构可使人们能深入了解他们与其他社团结构相区别的特质或信仰（汪小帆，2009）；在万维网中，不同的社团结构可以表示不同主题的主页集合（Gibson，1998；Flake，2002）；而在生物分子网络中，不同的社团结构往往是不同的功能性模块（Vespignani，2003）。而在产业R&D溢出网络中，不同的社团结构代表着不同的产业集群（李海威，2011）。在复杂网络演化的研究中，在同一社团的节点很可能会逐渐连接在一起，而R&D溢出网络中的节点表示不同的产业，因此在同一溢出集群的产业很可能由于R&D溢出而紧密关联。R&D溢出网络的聚类算法设计研究，是了解该网络组织结构和功能的重要方法，有助于理解R&D溢出内部结构的连接层次，对于如何科学地选择产业园的进园产业等具体问题具有重要意义。

1　　算法设计

随着复杂网络社团结构研究的不断深入，现已发展出许多划分复杂网络社团结构的算法。这些算法可按照不同的标准分为不同种类：如按照社团结构形成过程进行分类，算法可分为分裂算法、凝聚算法、搜索算法及其他算法（谱平分）等；按照算法的物理背景进行分类，算法可分为基于网络拓朴结构、基于网络动力学和基于Q函数优化及其他算法；根据节点是否只能属于一个社团进行分类，又可分为硬聚类和模糊聚类。上述划分社团的算法在判断标准、思路及步骤等方面各有不同，各有优缺点，因此有些研究者进行了对已有算法综合的研究，并提出一些新的算法，如Newman（2006）综合谱分析与Q函数算法等。

R&D溢出网络是加权有向复杂网络，且具有明显的层次（李海威，2011）。而在上述算法中，谱平分方法对于社团结构较清晰的复杂网络分析效率高，且理论基础建立在拉普拉斯 （Laplace）矩阵之上，较适合R&D溢出网络的社团结构分析。

根据Palla（2005）的研究发现，社团结构具有重叠性的重要特征。所谓重叠性是指复杂网络中有部分节点同时属于多个社团，重叠性在实际网络中体现得十分明显。传统的谱分析算法用标准化方法划分社团，也就是说一个节点只能归属于一个社团，但R&D溢出网络由许多互相重叠的社团构成，也就是说一个产业可能同时属于多个社团，因此模糊聚类方法划分的社团更能体现重叠性特征。

综上所述，根据R&D溢出网络特点，本文参照Newman（2006）及张世华等人（2007）的方法，综合谱分析方法及模糊c-均值聚类方法划分R&D溢出网络社团结构，然后用Q函数优化法选出最优的划分方法，进行R&D溢出网络的聚类算法设计研究。

1.1谱平分算法

谱平分方法是建立在邻接矩阵基础上的，主要思路是对邻接矩阵形成的Laplace矩阵（或标准矩阵）的特征值、特征向量进行分析，从而寻找社团结构（capocci，2005）。传统的谱平分方法是基于Laplace矩阵，计算速度快，但前提条件是已知社团个数。其在使用时有较大限制，因此，Capocci（2005）提出改进算法。该算法与传统谱平分算法不同，是基于标准矩阵N= K-1A。N的最大特征值总为1，其相应的特征向量称作平凡特征向量（trivial eigenvector）。Capocci等人（2005）还将谱平分算法扩展至加权有向网络。

1.2模糊c-均值聚类算法

模糊聚类方法中应用最广的是基于目标函数的模糊c均值聚类算法FCM（Fuzzy c-mean），Bezdek （1981）提出并建立了模糊c均值聚类理论。模糊聚类问题实质上是数学集合论问题。通常在实际应用中，还需要定义相似性或相异性的划分准则（目标函数），以及分析集合元素与模糊子集之间的相似度或失真度（目标函数距离最小），从而判定集合元素具体隶属于哪个模糊子集。而FCM则是建立在c均值目标函数的基础上。

FCM将n个向量xj∈X（1,2…,n）分成c个组Gi，并计算每组的聚类中心，使得c均值目标函数达到最小。FCM通过分析每个给定元素的隶属度来确定其属于各分组的程度。隶属度取值在［0，1］之间，每个元素的隶属度总和等于1。至于加权指数m的选择，Pal等人（1993）在聚类有效性实验中研究中得出m的最优选取区间为［1.5，2.5］，不作特殊要求情况下可取区间中值2，因此本文取m=2。

1.3 Q函数优化法

根据谱平分算法和FCM，我们可以得到多个网络社团划分，但仍难以判断划分的社团是否合理有效。因此，本文将参考Newman等人（2006）提出了Q函数优化法，构造适用于R&D溢出网络的Q函数度量社团划分的合理性。fortunato（2010）归纳了加权无向图、无权有向图及加权有向图的硬划分（每个节点只属于某个社团）情况下的Q函数。Nicosia等人（2009）还分析了Q函数的两个最重要的性质：性质1是当所有节点都同属于一个社团的时候，Q=0；性质2是Q值越高，则社团结构的划分越合理。并证明了式（6-13）所定义的Q函数是满足以上重要性质的。

由于R&D溢出网络为加权有向图，因此本文在fortunato和Nicosia等人的研究基础上，提出加权有向图的模糊划分Q函数为：

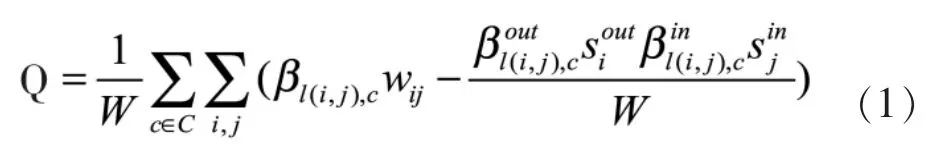
下面我们分析式（1）定义的Q函数的性质：

1）在所有节点都同属于一个社团的情况下，聚类数为1，Q=0。可见定义的Q函数满足性质1。

2）若网络的社团结构特征较显著时，若两个节点同属于一个社团，这时该两个节点的隶属度大小是相近的，从而产生的Q函数值为最大值，也就是说定义的Q函数满足模块性函数的第二个性质。

综上所述，式（1）满足Q函数最重要的二个性质，因此本文将用式（1）构造的Q函数度量R&D溢出网络社团划分的合理性。

1.4 R&D溢出网络社团算法

R&D溢出网络社团算法的思路是通过谱平分算法生成特征矩阵，然后运用FCM聚类算法进行聚类，并使模块性指标达到最大，最后选择Q值最大的社团划分结果。基本步骤如下：

2）计算标准矩阵Y=D-1WWT。

3）计算Yx=λx下的最大的K个特征值，并将其所对应的特征向量e1,e2,...,ek组成的矩阵Ek，其中K是社团数量的上界。

4）初始化k=2，并选择e1,e2,...,ek组成的矩阵Ek，在欧式范数下标准化的行向量。

5）使用FCM算法对Ek进行聚类，并划分R&D溢出网络为k个社团。

6）依据事先确定的阈值u，在计算得出的模糊隶属矩阵中确定社团结构，在本文中，阈值u为社团个数的倒数（1/k）。

7）令k增1，重复步骤3，4，5，直到k=K。

8）对于R&D溢出网络的K-1种划分结果，计算其Q函数值。

由于采用FCM算法进行聚类时，需生成值在0,1之间的随机数来初始化隶属矩阵，因此会导致单次聚类结果不稳定，出现误差。为减小聚类结果的误差，对上述算法进行改进，具体如下：

1）设定执行次数p，执行上述算法m次，计算m 次Q函数值的平均值。

2）选择Q函数平均值最大的划分方式n。

3）初始化L=1，初始化零矩阵U0。

4）在选择了最优的划分方式后，初始化k=n，执行FCM算法，得到模糊隶属矩阵UL。

5）对模糊隶属矩阵UL的列按从大到小次序排序。

6）令UL=UL+UL-1。

7）令L增1，重复步骤4和5，直至L=p。

8）计算Up/p，得到模糊隶属矩阵元素的平均值。

2　　实验结果

由于R&D溢出网络关邻矩阵D存在行为0的数据，因此D的逆矩阵不存在，即D为奇异。如果直接对D进行标准化会出现错误，因此需要对数据进行预处理，使其能够运用上述算法进行模糊聚类。我们对w中的每个元素进行极小量的偏移。使用MATLAB7.0软件按上述算法设计程序，将R&D溢出网络的关邻矩阵W作为初始数据，代入到设计的程序中去运行。运行100次后发现：当社团数目k=3，加权指数m=2时，对应的模块性Q函数平均值为最大值。社团数为3时Q函数平均值达到0.61，远超过Q函数值的下限0.3，划分结果可信。这说明将39个产业部门划分为3个社团是最优的划分结果，能够充分体现社团内部的关联较紧密，而社团之间的关联较稀疏的特点。而运行100次得到的平均模糊隶属矩阵与运行1000次得到的平均模糊隶属矩阵结果一致，表明算法运行100次后结果趋于稳定。通过以上实验得出本文设计的算法在加权有向复杂网络社区划分问题上的有效性，其检测结果稳定。

3　　结束语

在实际的复杂网络中，社团往往是模糊集。本文在谱平分、FCM算法的基础上，构建新的适用于加权有向复杂网络模糊划分Q函数，设计了复杂网络模糊聚类算法，并针对FCM聚类算法结果不稳定的现象进行了算法上的改进，使算法更适合于现实世界。最后，通过实验数据验证了设计的算法，结果从总体上提高算法的划分精确度，结果也趋向于稳定。本文设计的算法解决了从加权有向复杂网络、模糊集中发现、划分社团的问题。

［1］Bezdek J C. Pattern Recognition with Fuzzy Objective Function Algorithms［M］. New York：Plenum Press，1981.

［2］Capocci A,Servedio V D P，Caldarelli G，Colaiori F. Detecting communities in large networks［J］. Physica A，2005（7），352：669-676.

［3］Flake G W，Lawrence S R，Giles C L，et a.l：Self-organization and identification of web communities［J］. IEEE Computer，2002，35（3）：66-71.

［4］Fortunato S. Community detection in graphs. Physics Report［J］. 2010，486（2）：75-174.

［5］Gibson D，Kleinberg J，Raghavan P. Inferringweb communities from link topology［C］.//Proceedings of the 9th ACM Conference on Hypertext and Hypermedia. Pittsburgh：ACM Press，1998：225-234.

［6］HE D，JIN D，Baquero C，et a.l：Link Community Detection Using Generative Model and Nonnegative Matrix. Factorization［J］．PLOS ONE，2014，9（1）：e86899．

［7］Girvan M，Newman M E J. Community structure in social and biological networks［J］. Proc Natl A cad SciUSA，2002，99（12）：7821-7826.

［8］Newman M E J. Finding community structure in networks using the eigenvectors of matrices［J］. Phys Rev E，2006，74（3）：36104.

［9］Newman M E J. Modularity and community structure in networks［J］. Proc Natl A cad SciUSA，2006，103（23）：8577-8582.

［10］Nicosia V，Mangnioni G，Carchiolo V，Malgeri M. Extending the definition of modularity to directed graphs with overlapping communities［J］. physics，2009（3）：1-22

［11］Pal N R，Bezdek J C，Tsao E C K. Generalized clustering networks and Kohonen's self-organization［J］. IEEE Trans，1993，4（4）：549-557.

［12］Palla G，Derenyi I，Farkas I，et al. Uncovering the overlapping community structure of complex networks in nature and society［J］. Nature，2005，435（7043）：814-818.

［13］Pizzuti C，Rombo S E．Algorithms and Tools for Protein-Protein Interaction Networks Clustering，with a Special Focus on Populationbased Stochastic Methods［J］. Bioinformatics，2014，30（10）：1343-1352．

［14］Vespignani A. Evolution thinks modular［J］. Nature Gen，2003，35 （2）：118-119.

［15］Zhang S H，Wang R S，Zhang X S. Identification of overlapping community structure in complex networks using fuzzy c-means clustering［J］. Physica A，2007，374（1）：483-490.

［16］李海威. R&D溢出与产业发展关系研究［D］.中山大学，2011.

［17］汪小帆，刘亚冰.复杂网络中的社团结构算法综述［J］.电子科技大学学报，2009，38（5）：537-543.

李海威（1979-），男，高级工程师，博士，研究方向为复杂网络、聚类算法研究；韦天瀚（1994-），男，香港中文大学信息工程学院在读本科生。