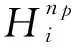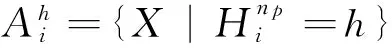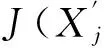一种改进式遗传算法优化分数阶PID控制器*

陈超波,胡　莉 ,马　颖，高　嵩,杨雪辉

(1.西安工业大学 电子信息工程学院,西安 710021；2.山东航天电子技术研究所,烟台 264670)



一种改进式遗传算法优化分数阶PID控制器*

陈超波1,胡莉1,马颖1，高嵩1,杨雪辉2

(1.西安工业大学 电子信息工程学院,西安 710021；2.山东航天电子技术研究所,烟台 264670)

摘要：为提高伺服控制系统的精度及响应速度.基于改进Oustaloup近似,采用改进式遗传算法对控制参数进行整定,提出了一种基于改进式遗传算法优化的分数阶PID控制器.在控制器的参数编码、适应度函数设计和进化机制选择上,引入竞争因子和优劣空间,选用自适应调节交叉概率和变异概率的方式,加快了优良子群的遗传进化,消除了传统遗传算法早熟和收敛性差等缺陷.将优化的整定结果应用到伺服系统模型中.通过时域性能仿真分析,结果表明：提出的改进式遗传算法分数阶控制器与传统PID控制器相比,具有更低的超调、更快的响应速度和更小的稳态误差,控制系统的动、静态性能显著优化,系统鲁棒性增强.

关键词：分数阶PID；改进式遗传算法；伺服系统；变异概率

自从1999年I.Podlubny对分数阶比例-积分-微分(Proportion-Integral-Derivative,PID)控制器[1]系统性能进行深入分析,其理论已日趋成熟.控制系统的性能分析一般是考虑系统的瞬态及稳态响应性能,结合其实际系统的控制效果,分析控制器的鲁棒性和稳定性等因素,随着在传统PID控制器的研究的深入,结合分数阶微积分理论,发现分数阶PID控制器比整数阶控制器具有更优的动态性能和强鲁棒性,其已广泛应用于物理学、材料学和建筑学等各个工程领域[2-4].分数阶控制器的设计及参数整定优化比传统PID控制器增加了整定难度及不确定性,但随着各种智能优化算法的深入研究,对分数阶PID控制器的设计也取得了一定的成果.文献[5]提出了一种对分数阶控制器参数进行智能调整的自适应的改进差分进化算法,结合实际被控对象构成的该闭环系统具有超调量小,上升时间快,稳定性好的优点.文献[6]用分数有限差分方法,建立分数阶延迟微分方程模型,对影响旅鼠群年生命周期的延迟系统进行了研究.文献[7]基于ARMAX模型的预测函数控制与分数阶比例积分相结合的控制算法,解决了预测控制模型失配和传统比例积分控制抗干扰性能差的问题.文献[8]提出了一种改进的基因遗传进化算法,这种算法是源于电磁理论的基于人群的启发式算法,使得优化的分数阶PID控制器作用于系统提高了系统的响应速度.文献[9]针对标准遗传算法(Simple Genetic Algorithm,SGA)易早熟、运行后期搜索速度慢等问题,提出了一种基于小种群策略的并行遗传算法来改善系统后期执行效率不高的性能.有效的解决了算法收敛速度与局部最优解之间的相互矛盾,针对非线性分数阶时滞微分方程的边值问题，求解出了不同种类的分数阶边界问题的近似解.

分数阶控制器在工程应用中起到越来越重要的作用,为了更好的对控制器进行参数求解,本文提出一种改进式遗传算法,该算法在分数阶控制器的参数编码、适应度函数的标定及进化机制上进行了分析,引入竞争因子和优劣空间,选用改善的自适应调节交叉变异概率的方式,将优良子群快速的遗传进化,淘汰更新适应力差的个体,克服了传统遗传算法的收敛性及稳定性的不足.通过实际伺服系统的仿真,验证了改进式遗传算法的有效性,以期提高被控系统的快速性和收敛性,同时使得系统具有更好的抗扰能力.

1分数阶微积分PID控制器

1.1分数阶微积分

分数阶微积分[10]是很好的建模工具,尤其是控制工程领域,分数阶微积分可以更加准确的描述应用对象[11-12].分数阶将整数阶微积分的阶次拓展到非整数,实质是任意阶微积分.函数f(t)的m阶微分为

(1)

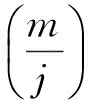
(2)

微积分算子为

(3)

式中：α为微积分的阶次,既可为整数也可以为分数；R(α)是α的实数部分.

分数阶微积分算子包含G-L定义和R-L定义,分数阶微积分G-L定义为

(4)

分数阶微积分R-L定义为

(5)

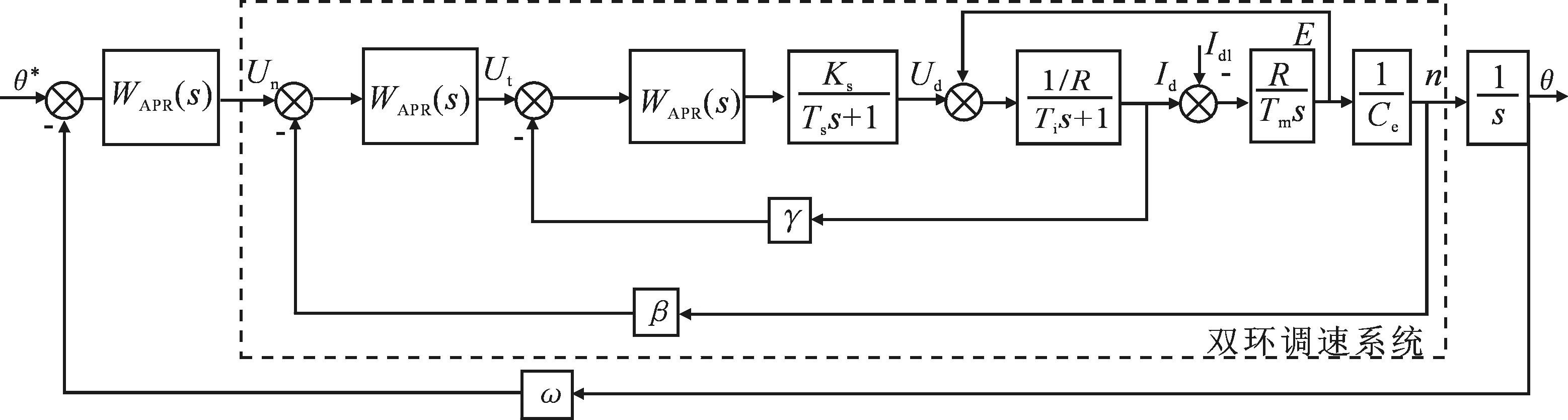
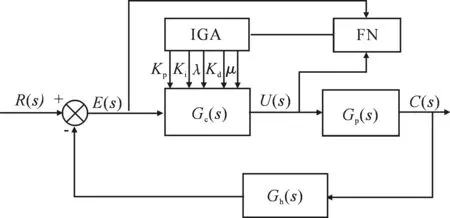
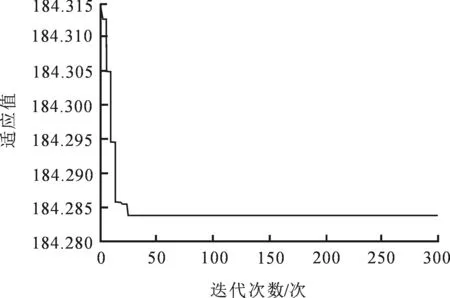
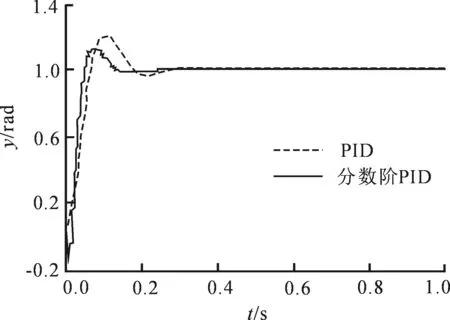
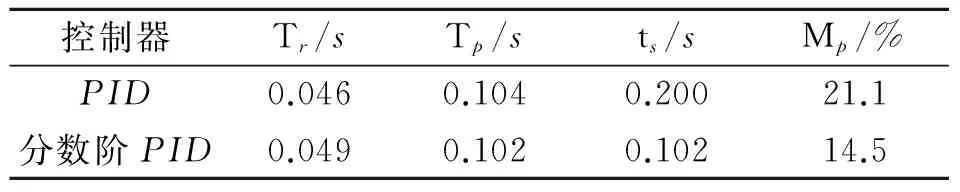
式中：m-1<α

1.2分数阶PID控制器

微积分算子通常用G-L定义可较精确的计算出给定信号的微积分,但这需要预先计算输入信号的采样值,不适用于控制系统仿真,故用滤波器算法逼近.本文采用改进Oustaloup滤波器近似法.

分数阶PID控制器比传统的整数阶PID控制器多了两个可变参数,这使得参数的整定更为复杂,其参数分别为比例系数KP、积分系数KI、微分系数KD、积分阶次λ和微分阶次μ,且当λ=μ=1时,分数阶PID控制器中的阶次从实数转换为整数,即可等效于整数阶PID控制器.分数阶PID控制器的输出可描述为

uc(t)=KPe(t)+KID-λe(t)+KDDμe(t)

(6)

式中：uc(t)为分数阶控制器的输出；e(t)为系统的误差及控制器的输入信号；D为微分算子.

由拉普拉斯变换,可得其传递函数为

(7)

其中Uc(s)和E(s)分别为分数阶控制器的输入和输出的拉氏变换.

2遗传算法的改进

遗传算法以生物界自然选择和自然遗传理论为基础,模拟自然界生物进化过程与机制来求解问题的一类自组织与自适应的人工智能技术[13-14].遗传算法具有随机选择的初始群体变量,一个适应度函数来评估每个个体在每一代的适应能力,这些个体进行复制、交叉和变异后产生新的下一代个体.遗传算法的可调参数较多,不同的参数配置对遗传算法的优化效果有显著影响,这对系统的控制参数的调整过程具有明显的不确定性,同时又可能不易找到最优参数而浪耗费机时.基于SGA的优化算法作为概率化的随机搜索方法,具有内在的隐并行性和全局寻优能力.但是,遗传算存在早熟和晚期收敛速度慢的现象,其原因主要是搜索过程中会丧失的种群多样性.因此,本文引入竞争因子和优劣空间等使良好种群个体较快地遗传进化,从而抑制早熟并增加种群的多样性.

2.1染色体构造编码和初始种群的生成

改进式遗传算法(ImprovedGeneticAlgorithm,IGA)对PID参数进行编码,构造出两个染色体,比例积分环节系数作为粗调参数分配给一个染色体,将微分环节的参数分配给另一染色体,均采用二进制字符集进行编码.用佳点集的方法随机生成一定数目的个体,对N个染色体编码的随机初始串数据作为初始点进行迭代,直到初始群体中的个体数目达到一定的规模,停止迭代.

2.2适应度函数值评估及标定

为了满足系统的动态特性,本文参考常见的误差绝对时间积分的性能指标和系统的调节时间确定系统的评价函数,为了防止控制量过大,引入输入的平方项.评价函数为

(8)

式中：w1、w2和w3为评价各个部分的权重值；e(t)为系统误差；u(t)为控制输入；ts为系统的调节时间.将目标函数做适当处理,可得适应度函数为

Fitness=1/J

(9)

为防止陷入局部最优,需要给予一定的限制,因此对适应度函数进行如下变换,即

Fitness′=e-βFitness

(10)

其中β为变换函数中的系数.β值越小,会强制选择那些趋向于适应度值大的种群个体.在优化后期,群体中个体适应度值通常非常接近,会导致不易收敛的情况发生,此时就需要放大个体适应度值,以提高选择能力.

2.3种群的选择及更新

SGA通常在解空间内使用一定随机方法产生一系列解集,并不能有效保证均匀分布,很可能始终群出现“早熟”情况.

i= 1,2,…,n；h= 0,1,2

(11)

式中：X为编码串序列；np为第n个染色体的p位的子编码串.当h为0时,将个体分到优空间集合；当h为1时,将个体分到劣空间集合；当h为2时,将个体分为空间需要补充的集合,一般视情况而定.划分优劣空间的标准为

(12)

在选择优质个体构成新的M个群体优劣空间中,继续将位数划分为高、中和低3个等级,以位数个数的均分比例末位淘汰制排挤,中等的前1/3位的位数可补充淘汰的部分,高等的作为父代进行交叉变异计算.

2.4自适应调整交叉变异率

遗传算法中使用交叉变异来产生新个体,通常用到的是固定交叉概率的点类的交叉算子和固定变异概率的基因位的变异算子,于是Srinvivas等提出了经典的自适应调整交叉概率和变异概率的方法,但是在进化初期会出现停滞现象,本文对经典自调整交叉概率Pc和变异概率Pv进行改进,即

(13)

(14)

式中：Fmax为最大种群的适应度值；Favg为每次迭代代种群的平均适应度值；F为要交叉的两个个体中的较大的适应度值(即选择算子中优劣空间中高等级适应度个体)；F’为变异个体的适应度值；Pc0为种群初始交叉概率；Pc1为提高后的种群交叉概率；Pv0为种群初始变异概率；Pv1为提高后的种群变异概率；k1和k2为变概率常数.

2.5优化分数阶PID算法

优化分数阶PID算法步骤：① 对分数阶PID参数按照经验范围分为分数阶积分和分数阶微分两部分,确定出各个参数上下限和精度，计算出二进制串位数进行参数编码.采用佳点集方法对参数群体进行初始化,包括初始子群的规模、搜索编码范围及最大迭代次数等.② 由设计的适应度函数,计算初始化的粒子适应度值、平均粒子的适应度值及当前适应度误差.③ 对初始化群体利用式(8)～(9)计算对应个体的适应度值并结合式(10)对适应度函数进行标定变换.④ 种群的遗传进化.利用

式(11)～(12)进行群体父代的选择,以保证选择出较好的适应度值个体,然后利用式(13)～(14)进行自适应交叉变异过程.⑤ 利用误差精度和迭代总次数判断是否满足结束条件,若满足则进行步骤⑥,否则返回步骤②.⑥ 将优化后的子群参数值[KP,KI,λ]和[KD,μ]进行解码并输出相应的适应度值.

3仿真及分析

3.1被控对象数学模型

本文将电流环和速度环看作由伺服电机及其驱动器构成的内部闭环结构,设计了分数阶PID控制器完成伺服系统最外环-位置环的控制.

伺服系统的结构框图如图1所示,其中虚线框内表示伺服系统双闭环调速系统作为位置环的被控对象.WAPR(s)、WAVR(s)、WACR(s)分别为位置调节器、速度调节器和电流调节器,ω，β和γ分别为位置、速度和电流反馈系数,θ*为给定位置信号,θ为位置输出信号.Un为速度输入,Ui为电流输入,Ud为电机输入电压,Id为电机电流输出,Idl为励磁电流,E为电枢回路电动势,n为电机转速,Ks为PWM变换器放大系数,Ts为变换器滞后时间常数,Ti为电枢回路电磁常数,Tm为电力拖动系统机械时间常数,Ce为电机反电动势系数，R为电枢电阻.

由图1伺服系统的结构,设计该系统的分数阶PID控制器参数整定框图如图2所示.FN为适应度函数评估；Gc(s)为位置环伺服控制器；Gp(s)为该伺服系统位置环的被控对象；Gh(s)为反馈通道传递函数.

R(s)为系统的位置输入,E(s)为系统误差信号,U(s)为被控对象的输入信号,即分数阶控制器的输出,C(s)为系统的输出信号的传递函数.

图1　伺服系统的结构框图Fig.1　Servo system block diagram

图2　分数阶控制器参数整定框图Fig.2　Parameter setting of fractional order controller

辨识结果利用连分式简化及降阶处理近似伺服系统模型[15],最后得到控制系统的开环传递函数为

G(s)=

(15)

式中：K1为等效伺服系统比例系数,其值为0.987；Kp、Ki、Kd、λ和μ为分数阶控制器的待求参数.

3.2模型仿真及分析

利用被控对象模型进行仿真验证,分别选取整数阶和分数阶控制对象进行仿真实验,其中,分数阶参数仿真实验选取参数为初始种群规模n=40,最大迭代步长iter_max=300次,交叉概率Pc0=0.85,变异概率Pv0=0.09,Kp∈[0,100],Ki∈[0,50],Kd∈[0,50],λ和μ∈[0,2]为搜索空间的上限和下限,计算得出的迭代后的算法曲线如图3所示.

图3　适应度变化曲线Fig.3　Fitness change curve

由图3可知,参数整定结果在迭代24次后可以取得满足精度的适应度函数的最小值.此时,得到的分数阶控制器为

(16)

传统PID方式整定出的整数阶控制器为

(17)

将用改进式遗传算法整定的分数阶控制器的参数、传统PID控制器及未施加控制器分别进行仿真,得到系统的单位阶跃响应如图4所示.其中t为仿真时间,y为系统仿真输出.

图4　不同控制器单位阶跃响应Fig.4　Unit step response of different controller

由图4可知,与传统PID控制器相比,分数阶控制器在保证控制精度的同时也改善了系统动态品质,减小了系统的超调并缩短了系统的调节时间,图4中各性能指标见表1,其中系统指标参数Tr、Tp、Mp分别为系统的上升时间、峰值时间和超调量,ts为系统调节时间.

表1　不同控制器下的系统时域性能指标Tab.1　Performance indicators in timedomain with different control systems

由表1可知,分数阶控制器在上升时间和峰值时间上改善不大,但在抑制系统振荡和进入稳态时间上面有良好的控制效果.

当t=0.3s时,给系统加一个幅值为0.2rad的扰动,此时系统的单位阶跃响应如图5所示.

由图5可知,分数阶控制系统在受到干扰后仍可以较快的恢复到稳定状态,与整数阶控制器相比,系统具有良好的抗干扰能力.优化后的分数阶控制器在系统受到一定的干扰后，仍可以使得系统具有良好的鲁棒性和动态响应，系统动态性能也较优化前明显改善.

图5　受扰动的单位阶跃响应Fig.5　Step response of the disturbance

4结 论

1) 针对简单遗传算法存在的早熟和收敛速度的问题,通过对自适应遗传算法进化初期的停滞现象进行分析,本文提出了一种改进式遗传算法来优化分数阶PID控制器.

2) 通过对实际伺服系统辨识模型进行数值模拟,结果表明该分数阶PID控制器优化时的收敛速度加快,保证了PID控制的实时性.

3)IGA优化的分数阶PID控制与传统PID控制相比,在系统的时域响应和抗干扰方面,优化后的分数阶PID控制系统具有较低的超调、较快的响应速度和良好的抗干扰性能.

参 考 文 献：

[1]PODLUBNYI.Fractional-orderSystemsandPI/Sup/SplLambda//D/Sup/SplMu//-Controllers[J].IEEETransactionsonAutomaticControl,1999,44(1):208.

[2]张俊峰,罗雄麟,袁毅夫.常减压装置旁路控制管壳式换热器的PID参数整定[J].石油化工自动化,2011,47(1):40.

ZHANGJunfeng,LUOXionglin,YUANYifu.PIDParametersTuningoftheTubeandShellHeatExchangerunderBypassControlinCDU[J].AutomationinPetro-ChemicalIndustry,2011,47(1):40.(inChinese)

[3]杨光祥,梁华,康秋红.两轮自平衡载运工具驱动电机分数阶PID控制器设计[J].机械科学与技术,2015,34(6):914.

YANGGuangxiang,LIANGHua,KANGQiuhong.DesigningFractionalOrderPIDControllerofDrivingMotorforaTwo-wheeledSelf-balancingVehicle[J].MechanicalScienceandTechnologyforAerospaceEngineering,2015,34(6):914.(inChinese)

[4]刘晓东,李绍铭.遗传算法的改进及其工程应用研究[J].工业控制计算机,2012,25(5):61.

LIUXiaodong,LIShaoming.ImprovementofGeneticAlgorithmandItsApplicationinEngineering[J].IndustrialControlComputer,2012,25(5):61.

(inChinese)

[5]黄丽莲,周晓亮,项建弘.分数阶PID控制器参数的自适应设计[J].系统工程与电子技术,2013,35(5):1064.

HUANGLilian,ZHOUXiaoliang,XIANGJianhong.Self-adjustingDesignonParametersoftheFractionalOrderPIDController[J].EngineeringandElectronics,2013,35(5):1064.(inChinese)

[6]MOGHADDAMBP,MOSTAGHIMZS.ANovelMatrixApproachtoFractionalFiniteDifferenceforSolvingModelsBasedonNonlinearFractionalDelayDifferentialEquations[J].AinShamsEngineeringJournal,2014,5(2):585.

[7]郭伟,陈一帆,周丽,等.无刷直流电机分数阶PI预测函数控制研究[J].武汉理工大学学报,2013,35(5):130.

GUOWei,CHENYifan,ZHOULi,etal.Fractinal-orderPIPredictiveFunctionControlResearchoftheBrushlessDCMotor[J].JournalofWuhanUniversityofTechnology,2013,35(5):130.(inChinese)

[8]LEECH,CHANGFK.Fractional-orderPIDControllerOptimizationviaImprovedElectromagnetism-likeAlgorithm[J].ExpertSystemswithApplications,2010,37(12):8871.

[9]胡振兴,李汪根.基于小种群策略的并行遗传算法[J].软件导刊,2013,20(2):33.

HUZhenxing,LIWanggen.ParallelGeneticAlgorithmBasedonSmallPopulationStrategy[J].SoftwareGuide,2013,20(2):33.(inChinese)

[10]PODLUBNYI.GeometricandPhysicalInterpretationofFractionalIntegrationandFractionalDifferentiation[J].FractionalCalculusandAppliedAnalysis,2002,5(4):367.

[11]BLANCHARDED,NGUYENCH.IdentificationandControlofaTrilayerConjugatedPolymerActuator[J].SmartMaterialsandStructures,2014,23(9):5025.

[12]BOHANNANGW.AnalogFractionalOrderControllerinTemperatureandMotorControlApplications[J].JournalofVibrationandControl,2008,14(9/10):1487.

[13]SRINIVASM,PATNAIKLM.AdaptiveProbabilitiesofCrossoverandMutationinGeneticAlgorithms[J].IEEETransactionsonSystems,ManandCybernetics,1994,24(4):656.

[14]SEKAJI,VESELV.RobustOutputFeedbackControllerDesign:GeneticAlgorithmApproach[J].IMAJournalofMathematicalControlandInformation,2005,22(3):257.

[15]高建龙.分数阶PID控制器在伺服系统中的应用及实现[D].南京:南京理工大学,2013.

GAOJianlong.ApplicationandImplementationofFractionalOrderPIDControllerinServoSystem[D].Nanjing:NanjingUniversityofScienceandTechnology,2013.(inChinese)

(责任编辑、校对张超)

【相关参考文献链接】

过晓芳.遗传算法的互补性产品定价策略研究[J].2013,33(5)：398.

谭宝成,廉春原,徐艾,等.一种基于改进遗传算法的机器人路径规划方法[J].2008,28(5)：456.

国亮,邓祥辉,国蓉.基于遗传算法的多项目资源约束优化问题研究[J].2007,27(6)：591.

李玉清,康筱锋,张建生,等.一类带工艺约束生产调度的随机梯度遗传算法[J].2007,27(3)：300.

张建生,康筱锋,李玉清,等.船舶尾流目标识别的随机梯度遗传算法研究[J].2007,27(1)：78.

苗荣霞,王彬.啤酒发酵温度的参数自整定模糊PID控制[J].2016,36(2)：167.

高嵩,王磊,陈超波,等.TS-PID算法的直流伺服控制系统[J].2016,36(1)：14.

国蓉,刘磊,孟祥众.圆柱零件加工用直线电机模糊自适应PID控制及建模[J].2015,35(12)：968.

薛航,贾培刚,何思锐,等.舰载稳定平台PIDNN控制系统设计与仿真[J].2015,35(4)：298.

郭全民,雷蓓蓓.汽车磁流变半主动悬架的模糊PID控制研究[J].2015,35(3)：192.

钟旭佳,高晓丁,严楠.电液比例压力控制系统的PID参数优化[J].2015,35(2)：106.

王昕炜,苗荣霞.锻造操作机大车行走机构的单神经元自适应PID控制[J].2014,34(12)：1012.

杨盛泉,刘海泉,王志安,等.台车式加热炉Fuzzy-PID复合控制系统[J].2013,33(7)：537.

谭宝成,马天力.无人车运动稳定性的模糊神经网络PID控制[J].2013,33(4)：334.

李聚锋,倪原,刘智平,等.某飞行器舵机控制的模糊PID算法[J].2013,33(3)：198.

谭宝成,康祖清.模糊PID算法在定型机温控系统上的应用[J].2012,32(11)：895.

张荷芳,王洁,易善伟.基于Smith预估的模糊PID串级中央空调水系统控制[J].2012,32(4)：330.杨盛泉,刘白林,裴昌幸.灰色预测PID模型的建筑构件耐火试验炉控制系统[J].2012,32(4)：315.

秦刚,王新茹.PID结构广义预测控制算法的仿真及分析[J].2012,32(2)：162.

谭宝成,于向恩.变结构PID在铸坯去毛刺机中的应用[J].2012,32(2)：147.

秦刚,陈凯,高惠中,等.内模PID控制器在智能车转向系统中的应用及仿真[J].2011,31(7)：649.

杨盛泉,刘白林,刘萍萍,等.基于DMC-PID复合算法的温度控制器的设计[J].2011,31(5)：459.

谭宝成,党莉.变速积分增量式PID在气力除灰控制系统中的应用[J].2010,30(5)：478.

谭宝成,成法坤.自适应模糊PID在中频弯管机温度控制中的应用[J].2010,30(2)：191.

谭宝成,王大为,俞开文.变结构PID在锻造操作机控制系统中的应用[J].2009,29(5)：466.

王航宇,倪原.基于卡尔曼滤波器的电动汽车PID控制系统设计[J].2008,28(3)：267.

樊泽明,冯卫星,王亮,等.智能阀门定位器PID单参数模糊自适应控制设计[J].2007,27(6)：563.

来跃深,司瑞强.专家PID控制器的CPLD设计[J].2007,27(5)：421.

高嵩,朱峰,肖秦琨,等.机载光电跟踪系统的模糊自整定PID控制[J].2007,27(4)：312.

DOI:10.16185/j.jxatu.edu.cn.2016.06.014

*收稿日期：2015-09-15

基金资助：兵器预研支撑基金(62201070317)；陕西省国际科技合作重点项目(2015KW-024)

作者简介：陈超波(1978-)，男，西安工业大学副教授，主要研究方向为智能控制、模式识别.E-mail：choby@xatu.edu.cn.

文献标志码:中图号：TP273A

文章编号：1673-9965(2016)06-0510-07

Improved Genetic Algorithm for Optimal Fractional-Order PID Controller

CHENChaobo1,HULi1,MAYing1,GAOSong1,YANGXuehui2

(1.School of Electronic Information Engineering,Xi’an Technological University,Xi’an 710021,China;2.Shandong Institute of Aerospace Electronics Technology,Yantai 264670,China)

Abstract:In order to enhance the accuracy and response speed of servo control system,based on improved Oustaloup approximation,an improved genetic algorithm in optimal fractional order PID controller is proposed.The competition factor and the pros and cons of space are induced,and the adaptive crossover rate and mutation rate are selected,to accelerate the evolution rate of excellent subgroup and eliminated the premature and poor convergence of traditional genetic algorithm.Optimized results are applied in servo system model.The simulation and analysis in time-domain show that the proposed improved genetic algorithm of fractional order controllers is better than the conventional PID controller in faster response speed,lower overshoot and smaller steady-state error,as well as excellent dynamic and static properties and strong robustness.

Key words:fractional order PID controller; improved genetic algorithm; servo system; mutation rate