空间动态面板模型的时间滞后效应检验

孙　荣

(重庆工商大学 数学与统计学院， 重庆 400067)



空间动态面板模型的时间滞后效应检验

孙荣

(重庆工商大学 数学与统计学院， 重庆 400067)

摘要：空间面板数据模型由于考虑了经济变量间的空间相关性，其优势日益凸显,已成为计量经济学的热点研究领域。将空间相关性与动态模式同时扩展到面板模型中的空间动态面板模型，不仅考虑了经济变量之间的空间相关性，还考虑了时间上的滞后性，是空间面板模型的发展，增强了模型的解释力。考虑一种带固定个体效应、因变量的时间滞后项、因变量与随机误差项均存在空间自相关性的空间动态面板回归模型，提出了在个体数n和时间数T都很大，且T相对地大于n的条件下空间动态面板模型中时间滞后效应存在性的LM和LR检验方法，其检验方法包括联合检验、一维及二维的边际和条件检验；推导出这些检验在零假设下的极限分布；其极限分布均服从卡方分布。通过模拟试验研究检验统计量的小样本性质，结果显示其具有优良的统计性质。

关键词：空间动态面板模型；时间滞后效应；LM检验；LR检验

一、引言

空间相关性的存在导致空间数据在经典统计学理论的应用中产生问题，为了分析这种空间相关性，Clif等人于 1973年提出了空间自回归模型(the spatial autoregressive model, SAR)[1]120-184。这种模型不仅考虑了空间相关性，也将时间依赖性纳入其中，综合了普通面板数据模型方法、传统时间序列方法和横截面方法。在SAR模型的基础上形成的空间面板数据模型由于具有更高的自由度、涵盖更丰富的信息量、减少了变量间的共线性、提高了模型估计的有效性等优点，引起了学者浓烈的兴趣。对于空间面板模型检验问题的研究主要有：Anselin等研究了空间相关性的检验问题[2][3]90-132[4-6]；Baltagi 等分析了随机个体效应与剩余误差项序列空间相关性的联合检验问题[7]，这些研究都没有考虑剩余误差序列中的剩余项相关性问题。Baltagi等提出了一种存在随机个体效应、剩余误差序列存在空间相关且剩余误差序列中的随机扰动项是AR(1)过程的空间面板模型，建立了这种模型的个体效应、空间相关性、AR(1)过程的联合、边际与条件的LM与LR检验方法[8]， Myoung Jin Jang 等提出了对于存在随机时间效应、随机误差项存在空间自相关的面板模型在n固定T趋于无穷大或者T固定n趋于无穷大的随机时间效应、空间相关性的联合、边际与条件的LM与LR检验方法[9]。这些检验方法针对的模型并没有把时间滞后的因变量作为动态结构纳入面板模型中，而将空间相关与动态模式同时扩展到面板数据模型中的空间动态面板模型，不仅考虑了经济变量的空间相关性还考虑了时间上的滞后性，增强了模型的解释力。本文提出了一种带固定个体效应、因变量的时间滞后项、因变量与随机误差项均存在空间自相关性的空间动态面板回归模型；建立了在个体数n和时间数T都很大，且T相对地大于n的条件下时间滞后效应存在性的LM和LR检验方法，其检验方法包括联合检验、一维、二维的边际和条件检验；推导出了这些检验在零假设下的极限分布，其极限分布均服从卡方分布。这些检验方法是对Baltagi等学者提出的空间面板模型检验方法的发展，运用统计模拟方法对这些检验统计量的小样本性质进行了研究，其结果显示除了极少的算例表现出较明显的水平扭曲与较低的经验势之外，其他算例都具有较好的统计性质。

二、模型设定与似然函数

(一) 模型设定

本文考虑的基本模型是：

Ynt=λWnYnt+γYnt-1+Xntβ+Cn0+Unt

Unt=ρMnUnt+Vnt

(t=1,2,…,T)

(1)其中，Ynt=(y1t,y2t,…,ynt)′；Vnt=(v1t,v2t,…,vnt)′是n×1列向量，vit是关于i和d独立同分布、均值为0、方差为σ2的随机变量；Wn是n×n非随机的空间权重矩阵。这一矩阵决定了因变量的空间相关性；Xnt是n×k非随机解释变量矩阵；Cn0是n×1固定效应的列向量；Mn是n×n非随机的随机误差项的空间权重矩阵, 这一矩阵决定了随机误差项的空间相关性，因此模型的参数就是(λ,γ,β′,ρ,σ2)，定义θ=(λ,γ,β′,ρ,σ2)，对任意的λ与ρ，S(λ)=In-λWn,R(ρ)=In-ρMn。(λ,γ,ρ)取值于一紧的参数空间。

(二) 准极大似然函数

为了估计相关参数简化模型，本文运用Lee等人提出的变换方法，得到准极大似然函数[10]。

(2)

其中：

(3)

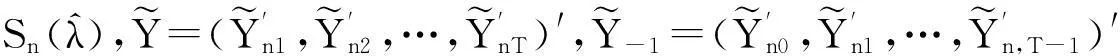
三、检验统计量与定理

(一)检验统计量

利用相关文献方法，我们提出在零假设下的LM检验统计量：

(4)

(二) 联合检验H0∶λ=γ=ρ=0

联合检验即是检验模型是否同时不存在因变量的时间滞后效应、因变量及随机误差项的空间相关性。

利用式(2)、式(3)可得到：

(5)

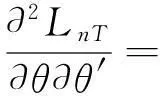
(6)

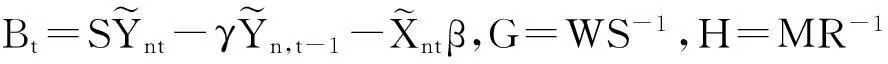
由式(2)、(3)、(5)得到参数θ=(λ,γ,ρ,σ2)无约束QMLE，其中：

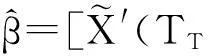
(7)

由式(2)、(3)、(5)得到参数θ=(λ,γ,β′,ρ,σ2)有约束QMLE，其中：

(8)

因此，在零假设成立条件下，由式(5)、(6)、 (8) 及假定1，得到：

(9)

(10)

由式(4)得到联合LM检验H0∶λ=γ=ρ=0的统计量为：

(11)

由式(3)、(7)可得到联合LR检验H0∶λ=γ=ρ=0统计量为：

LRJ=2(LU-LR)

(三) 时间滞后性检验

因变量的时间滞后效应检验包含一维与二维的条件检验与边际检验，其中二维检验包括因变量时间滞后性与随机误差序列空间相关性检验、因变量时间滞后性与空间相关性检验。

1.一维条件检验

1)一维条件检验：一维条件检验既是在允许存在因变量及随机误差项存在空间相关性的条件下即λ≠0与ρ≠0，检验λ=0成立与否。

由式 (2)、(3)、(5)得到参数θ=(λ,γ,β′,ρ,σ2)有约束QMLE，其中：

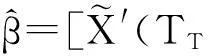
(12)

由式(5)、(12)得到：

(13)

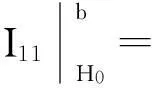
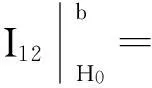
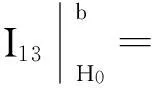
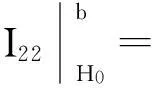
(14)

由式(12)、(13)、(14)得到条件LM检验统计量，记为LMγ：

由式(7)、(12)得到条件LR检验统计量，记为LRγ：

LRγ=2(LU-LR)

参数θ=(λ,γ,β′,ρ,σ2)无约束QMLE与式(7)相同。

2)一维边际检验

一维边际检验是在不存在因变量和误差序列空间相关性的条件下即λ=ρ=0时检验H0∶γ=0成立与否。当λ=ρ=0,S与R都简化为单位阵。在零假设成立的条件下，由式(2)、(3)、(5)得到参数θ=(λ,γ,β′,ρ,σ2)有约束QMLE，其中：

这样，边际的LM检验统计量记为LMγ/λρ：

LMγ/λρ

由式(7)、(12)得到边际LR检验统计量，记为LRγ/λρ：

LRγ/λρ=2(LU-LR)

2.因变量时间滞后性及随机误差序列空间相关性检验H0∶γ=ρ=0

1)二维条件检验

二维条件检验即当λ≠0时检验H0∶γ=ρ=0成立与否。

在零假设成立条件下，由(2)、(3)、(5)得到参数θ=(λ,γ,β′,ρ,σ2)有约束QMLE，其中：

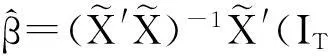
(15)

由式(5)、(15)得到：

(16)

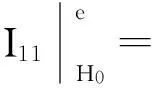
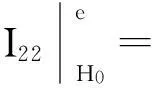
(17)

由式(15)、(16)、(17)得到条件LM检验统计量，记为LMγρ：

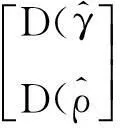
由式(7)、(15)得到条件LR检验统计量，记为LRγρ：

LRγρ=2(LU-LR)

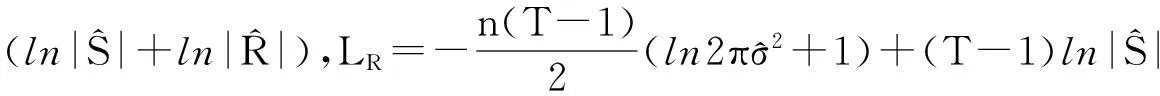
2)二维边际检验

二维边际检验即当λ=0时检验H0∶γ=ρ=0成立与否。

当零假设成立时，R与S变为单位矩阵,由式(2)、(3)、(5)得到参数θ=(λ,γ,β′,ρ,σ2)有约束QMLE，其中：

(18)

由式(16)、(17)、(18)得到边际LM检验统计量，记为LMγρ/λ：

由式(7)、(18)得到边际LR检验统计量，记为LRγρ/λ：

3.因变量时间滞后与空间相关性检验

1)二维条件检验H0∶λ=γ=0

二维条件检验即是在ρ≠0时检验H0∶λ=γ=0成立与否。

在零假设成立条件下，由式(2)、(3)、(5)得到参数θ=(λ,γ,β′,ρ,σ2)有约束QMLE，其中：

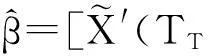
(19)

由式(5)、(19)得到：

(20)

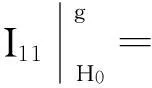
(21)

由式(19)、(20)、(21)得到条件LM检验统计量，记为LMλγ：

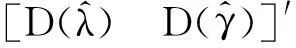
由式(7)、(19)得到条件LR检验统计量，记为LRλγ：

LRλγ=2(LU-LR)

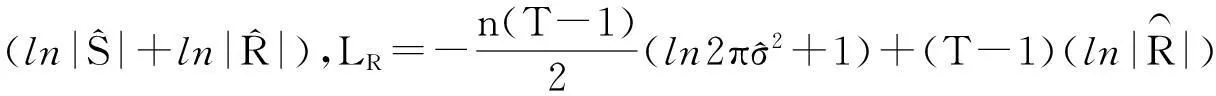
参数θ=(λ,γ,β′,ρ,σ2)无约束QMLE与式(7)相同。

2)二维边际检验

二维边际检验H0∶λ=γ=0即是在ρ=0时检验H0∶λ=γ=0成立与否。

在零假设成立条件下，由式(2)、(3)、(5)得到参数θ=(λ,γ,β′,ρ,σ2)有约束QMLE，其中：

(22)

由式(20)、(21)、(22)得到边际LM检验统计量，记为LMλγ/ρ：

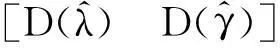
由式(7)、(22)得到边际LR检验统计量，记为LRλγ/ρ；

LRλγ/ρ=2(LU-LR)

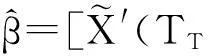
(四)定理

为了推导出检验统计量的极限分布,需要如下的相关假定：

假定1Wn与Mn是实对称的常数矩阵，其对角线元素满足：Wn,ii=0,Mn,ii=0,i=1,2,…,n。

假定2扰动项{vit}i=1,2,…,n,t=1,2,…,T，T是关于i和d独立同分布、均值为0，方差为σ2随机变量。对某些η>0,E|vit|4+η<∞。

假定3Sn(λ)对所有的λ非奇异,R(ρ)对所有的ρ非奇异。

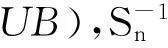
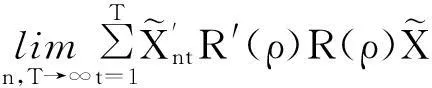
假定6n和T都非常大，且T相对的大于 n。

假定1为空间权重矩阵的一项正规化要求，常数矩阵表示权重不发生时变，利于参数估计的方便。Wn与Mn的空间主对角元素为0表示空间个体与自身不存在空间联系，可以避免出现空间自影响[11]；假定2是SAR模型为了保证估计量一致性的一般假定；假定3矩阵的非奇异性假定也是为了得到参数估计量的方便；假定4行和与列和的一致有界性假定是为了将空间与时间上的相关性限定在一定的范围，如果空间与时间的相关性都存在衰减变化，那这一假定就是合理的。由JihaiYua及Lee,L.F.的相关研究结论可知[10，13]；假定5和6是保证参数QMLE收敛性、获得λ与ρ估计参数可识别性的一致可识别、一致收敛与一致等度连续三条件的基本条件；假定7是保证得到统计量极限分布的重要条件，对于模型(1)加上在参考文献[10]、[12]、[13]中其他类似的相关条件，假定7可成立。

当T，n→∞，有：

定理3(a)当假定1～7成立, 当γ=ρ=0。假设∀λ

(b)当假定1～7成立，当H0∶λ=γ=0，假设∀ρ,n/T→0

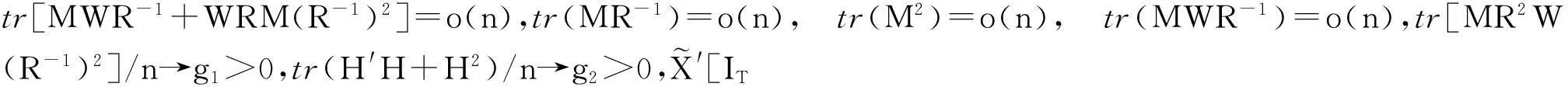
当T，n→∞,那么：

四、检验统计量的有限样本性质

统计模拟的基本模型为：

Ynt=λWnYnt+γYnt-1+Xntβ+Cn0+Unt

Unt=ρ0MnUnt+Vnt

其中，β=0.4；Xnt、Vnt和Cn0分别来自独立正态分布；Wn和Mn是rook矩阵,空间自相关因子λ和ρ变化取值为( 00.20.40.6 ),

γ取值为=( 0

0.30.50.8)。个体个数n分别为10，30，时间个数T分别为25和100。各种LM和LR检验模拟重复1 000次。

(一)联合检验H0∶λ=γ=ρ=0

表1给出了重复1 000次，n=10，30、T=25，100条件下，在 5%名义显著性水平下的H0∶λ=γ=ρ=0联合LM检验与LR检验经验水平与势。从表1可以看出，在5%的显著性水平下，当n=10和T=25两种检验的经验水平略高于名义水平 ，变化范围在6.4%与7%之间；当n=30和T=100，略低于5%变化范围在3.8%和4.8%之间。从检验统计量的检验势来看，当n和T较大时的拒绝概率要高于n和T较小时，保持了一个合理的拒绝水平。

表1　联合检验H0统计量经验水平与势

(二)检验H0∶γ=ρ=0

表2给出了重复1 000次，n=10，30、T=25，100条件下，在5%名义显著性水平下的H0∶γ=ρ=0条件与边际LM检验与LR检验经验水平与势。从表三可以看出，除了γ=0,λ=0.2,ρ=0时，两种检验的经验水平与名义水平并没有显著区别，变化范围在4.6%与7.8%之间。当n和T增加时，经验势水平亦随之改善，表现出一个合理的拒绝水平。

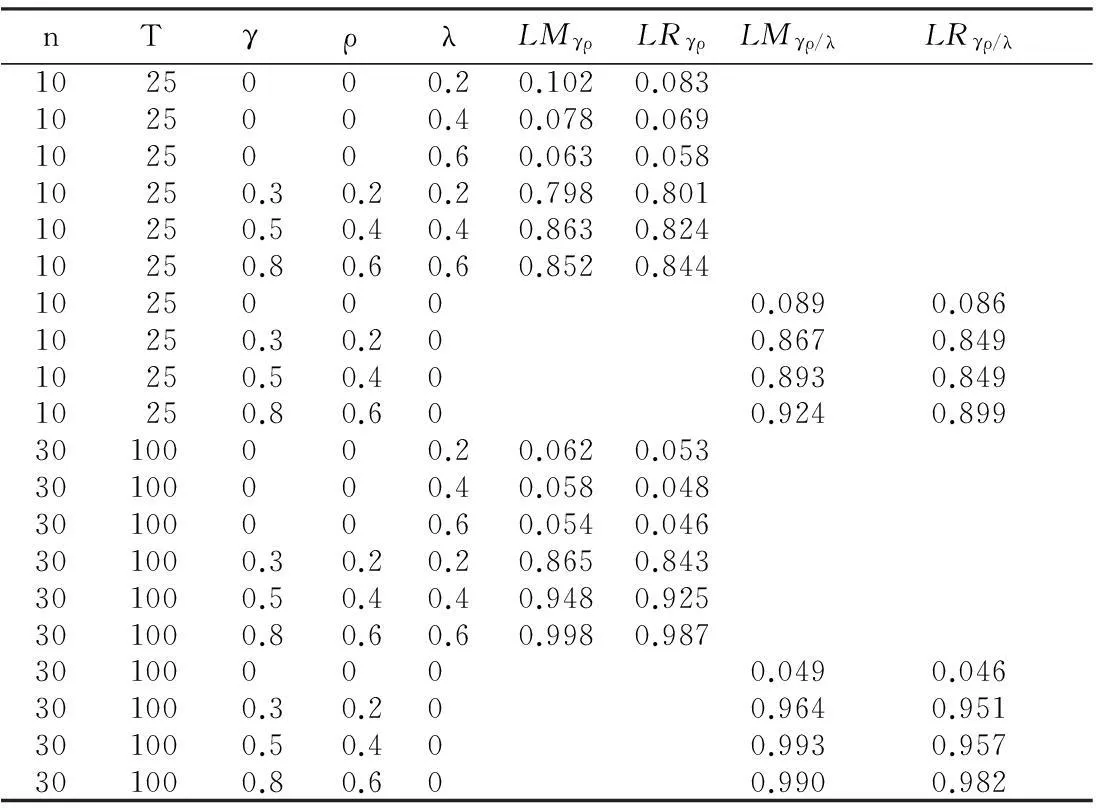
表2　检验H0∶γ=ρ=0统计量经验水平与势

五、结 论

空间面板数据模型因为分析了经济变量的空间相关性而成为空间计量经济学中重要的模型之一，而把空间相关性与时间滞后性同时扩展到空间面板形成的空间动态面板模型，是对空间面板模型的发展与完善。本文提出了一种带有固定个体效应，因变量时间与空间滞后项及随机误差项具有空间相关性的动态面板模型，这个模型是对Anselin、L.Florax、RAnselin等相关论文中模型的一个推广，对这种模型提出了在n和T都比较大，且T相对地大于n的时间滞后效应的检验问题，内容包括因变量时间滞后性、空间相关性与随机误差项的空间相关性联合检验、一维和二维的条件与边际检验，建立了LM和LR检验统计量，得出了这些检验统计量在零假设条件下的极限分布。从统计模拟结果来看，除了一些个别结果之外，整体来看，本文所提出的检验统计量具有较好的统计性质。

参考文献：

[1]Cliff A D, Ord J K. Spatial Autocorrelation[M]. London: Pion Ltd.,1973.

[2]Anselin L, Florax R. Small Sample Properties of Tests for Spatial Dependence in Regression Models: Somefurther Results[C]// Anselin L, Florax R. New Directions in Spatial Econometrics. Berlin: Springer, 1995.

[3]Anselin L. Spatial Econometrics: Methods and Models[M]. Dordrecht: Kluwer Academic, 1988.

[4]Anselin L, Bera A K. Spatial Dependence in Linear Regression Models with an Introduction to Spatial Econometrics[C] // Ullah A, Giles D E A. Handbook of Applied Economic Statistics. New York: Marcel Dekker, 1998.

[5]Kelejian H, Robinson D. A Suggested Test for Spatial Autocorrelation and/or Heteroskedasticity and Corresponding Monte Carlo Results[J].Reg. Sci. Urban Econ. 1998,28 (4).

[6]Anselin L. Raos Score Test in Spatial Econometrics[J]. J. Statist. Plann. Inference, 2001, 97 (1).

[7]Baltagi B H, Song S H, Koh W. Testing Panel Data Regression Models with Spatial Error Correlation[J]. J. Econometrics,2003, 117 (1).

[8]Baltagi B, Song S H, Jung B C, Kon W. Testing for Serial Correlation, Spatial Autocorrelation and Random Effects Using Panel Data[J]. Journal of Econometrics, 2007, 140 (1).

[9]Myoung Jin Jang, DongWan Shin. Tests for Random Time Effects and Spatial Error Correlation in Panel Regression Models[J]. Statistics, 2014,48(1).

[10]Lee L F, Yu J. Estimation of Spatial Autoregressive Panel Data Models with Fixed Effects [J].Journal of Econometrics,2010, 154 (2).

[11]邓明，钱争鸣. 混合形式的变系数空间面板数据模型[J].数理统计与管理,2014,33(3).

[12]Su L, Yang Z, Su L, et al. QML Estimation of Dynamic Panel Data Models with Spatial Errors[J]. Journal of Econometrics, 2007, 185,(1).

[13]Jihai Yua, Robert de Jong, Lung-fei Lee. Quasi-maximum Likelihood Estimators for Spatial Dynamic Panel Data with Fixed Effects When Both n and T are LargeI[J]. Journal of Econometrics, 2008, 146 (3).

(责任编辑：崔国平)

收稿日期：2015-11-06

基金项目：重庆市教委科技项目《人口老龄化背景下的社会养老保险隐性债务精算模型与应用研究》(KJ1400619)

作者简介：孙荣，男，四川宣汉人，硕士，副教授，研究方向：应用统计，计量经济学。

中图分类号：F224.0∶F064.1

文献标志码：A

文章编号：1007-3116(2016)07-0022-08

Tests for Time Lag Effects in Spatial Dynamic Panel Data Models

SUN Rong

(College of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067, China)

Abstract:Spatial panel data model considered spatial correlation between the economic variables, its advantage has become increasingly prominent, and become a hot research field of econometrics. Spatial dynamic panel model which simultaneously included the spatial correlation and the dynamic setting considered not only the economic variables of spatial correlation, but also the time lag, it was a development on the panel model, and enhanced the interpretation force. this paper considers a spatial dynamic panel data regression model with fixed region effects, time lagged spatial dependent variables, correlation of dependent variables and residual disturbances among cross sectional units. When the number of individuals , the number of time periods are large, and is asymptotically large relative to , the paper derives various Lagrange multiplier tests and likelihood ratio test statistics for this panel data regression model including tests for lag effects, in jointly, marginally and conditionally (one-dimensional and two-dimensional) . Limiting null distributions of the tests are derived, the limit distribution are all subject to chi-square distribution. Size and power performances of the proposed tests are compared by a Monte-Carlo experiment. Monte Carlo evidence shows their good size properties and power properties.

Key words:dynamic spatial panel model; time lag effect; lagrange multiplier tests; likelihood ratio tests

【统计理论与方法】