直升机机动飞行对尾传动轴临界转速的影响

陆凤霞, 朱如鹏, 倪　德

(1.南京航空航天大学 机电学院,南京　210016；2.中国航空动力机械研究所, 湖南　株洲　412002)

直升机机动飞行对尾传动轴临界转速的影响

陆凤霞1, 朱如鹏1, 倪德2

(1.南京航空航天大学 机电学院,南京210016；2.中国航空动力机械研究所, 湖南株洲412002)

直升机的平动分量和尾传动轴的位置参数均不影响传动轴的临界转速，仅直升机的转动分量对传动轴临界转速产生影响。通过几种典型机动飞行分析了直升机各转动分量对尾传动轴临界转速的影响。结果表明：偏航角速度与水平轴的临界转速近似呈抛物线关系，而与尾斜轴的临界转速近似呈线性关系且为左右对称图形；随着尾斜轴倾斜角的增大，对称轴向左偏移；俯仰角速度对尾传动轴临界转速的影响与偏航角速度相同；横滚角速度与水平轴和尾斜轴临界转速之间均呈线性关系，且随尾斜轴倾斜角的增大，对称轴向右偏移；传动轴第二阶临界转速变化曲线的对称轴对应角速度大小近似为第一阶临界转速时的16倍。

直升机；尾传动轴；机动飞行；弯曲振动；临界转速

直升机尾传动轴负责传递运动和动力给尾桨，其性能优劣对直升机整体性能有重要影响。服役中，直升机为一非惯性系，将在直升机的部件上作用附加载荷[1-2]，从而对其动力学特性产生不利影响。因此，有必要研究直升机的机动飞行对其尾传动轴动力学特性的影响。

目前，关于机动飞行对发动机转子系统振动的影响研究较多。祝长生等[3-4]建立了考虑空间机动飞行和发动机安装位置影响的多质量、多盘和多支承柔性转子系统动力学模型，并分析了几种典型机动飞行对转子系统振动特性的影响。林富生等[5-9]深入研究了飞行器速度和加速度对发动机等变速运动转子系统、有初始弯曲转子系统、裂纹转子系统、SFD-转子系统和碰摩转子系统动力学特性的影响，获得了很多重要的结论。徐敏等[10-11]对水平盘旋和俯冲拉起两种机动飞行状态下双盘悬臂转子和带挤压油膜阻尼器的Jeffcott转子的振动特性进行了研究。顾致平等[12]分析了飞机水平盘旋时刚性和弹性两种支承型式下Jeffcott转子的振动特性。杨永锋等[13-14]研究了俯冲拉起和水平盘旋对裂纹转子系统动力学特性的影响。然而这些研究均将轴段看作无质量的弹簧，并不适合具有质量连续分布特征的直升机尾传动轴。许兆棠[15]研究了直升机水平和垂直方向加速度对其尾传动轴动力学特性的影响，但是未考虑直升机转动的影响。倪德等[16]建立了直升机空间机动飞行下尾传动轴的横向弯曲振动模型，分析了直升机机动飞行对其尾传动轴中心运动轨迹的影响。本文将在文献[16]的基础上，研究直升机机动飞行对其尾传动轴临界转速的影响。

1考虑直升机机动飞行的尾斜轴动力学模型

1.1坐标系统与运动描述方法

如图1所示，选取直升机在地球上的起飞位置O0为原点，建立坐标系O0x0y0z0，O0z0轴的指向与直升机的前飞方向相反，则直升机的平动运动可用坐标系O0x0y0z0的平动分量[X0，Y0，-Z0]T来描述。取直升机的重心OR为原点，建立与机身对称轴相重合(ORzR轴)的坐标系ORxRyRzR，则直升机的转动运动可用坐标系ORxRyRzR上的转动分量[θxR，θyR，-θzR]T来描述。θxR为直升机的偏航角，θyR为俯仰角，θzR为横滚角且转向与正横滚方向相反。以尾斜轴的最左端轴颈中心O为原点，建立与坐标系ORxRyRzR相平行的坐标系Ox1y1z1，然后绕Oy1轴逆时针旋转φ角，建立坐标系Oxbybzb。φ角为尾斜轴与水平轴之间的夹角，φ=0时即为水平轴。则尾斜轴任意截面的横向运动可采用坐标系Oxbybzb中的运动分量uzb和vzb来描述。原点O与OR之间的距离在坐标系ORxRyRzR中各坐标轴上的投影分别为u0、v0和w0，称之为尾斜轴的位置参数。图中，l为尾斜轴的长度，ezb和φe0分别为轴截面质心相对于几何中心的偏心距及其初始相位角，ωφ为尾斜轴的角速度。尾斜轴采用空心轴，内径为d，外径为D。

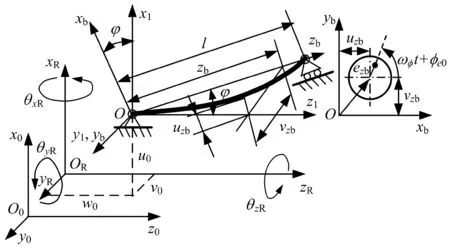
图1　直升机机动飞行下描述尾斜轴横向运动的坐标系统Fig.1 Coordinate system for describing lateral bending vibration of helicopter oblique tail drive shaft during maneuvering flight

1.2动力学方程

根据图1所建立的坐标系统，推导考虑直升机机动飞行影响的尾斜轴动能与势能计算公式，再利用哈密顿原理即可得到本文作者在文献[16]中推导的考虑直升机机动飞行影响的尾斜轴动力学偏微分方程(参见文献[16]中的式(3)和式(4))。利用分离变量法将uzb和vzb分解为固有振型函数和描述运动规律的时间函数的乘积，然后利用伽辽金计算方法，将上述偏微分方程转化为常微分方程(参见文献[16]中的式(6))，可采用常微分方程理论对其进行分析，简化了分析过程。令文献[16]的式(6)中由于直升机机动飞行引起的附加激励项和由于尾斜轴质量偏心引起的不平衡力项等于0，即可得到考虑直升机机动飞行的尾斜轴自由振动的运动方程为

(1)

式中：

Fa0=ρAglsinφ

式中：(·)表示对时间t求导，(′)表示对位置zb求导，p为尾斜轴的密度，A为轴截面的面积，E为尾斜轴材料的弹性模量，I为轴截面关于中性轴的惯性矩，Fa0为尾斜轴承受的总轴向力，Wr为尾斜轴的第r阶固有振型函数，是描述轴截面位置为zb时的横向振动幅值函数，qur和qvr为描述尾斜轴运动规律的时间函数，g为重力加速度。

2直升机机动飞行对尾斜轴临界转速的影响

(2)

式中：Aur和Avr为运动幅值，e为自然指数，s为Laplace域内的复变量。将式(2)代入式(1)中并写成矩阵形式有

(3)

由于系统振动时，Aur和Avr不能为0，所以，式(3)中的系数矩阵的行列式应等于0，即

(Kr+Kur+s2Mr)(Kr+Kvr+s2Mr)-[Kuvr+s(ωφGyr+Cr)][Kvur-s(ωφGyr+Cr)]=0(4)

令式(4)中的s=jωr且ωφ=ωr，然后求解该一元四次方程，即可得到直升机机动飞行下尾斜轴的临界转速。然而，式(4)很难直接获得解析解，所以本文采用二分法进行求解。

目前，直升机尾传动轴有亚临界和超临界两种设计方案，前者工作于第一阶临界转速之下，后者工作于第一阶和第二阶临界转速之间。因此，本文主要分析直升机机动飞行对尾传动轴前两阶临界转速的影响。取尾传动轴的计算参数为：d=84 mm，D=90 mm，l=1.65 m，E=70 GPa，G=27 GPa，ρ=2 800 kg/m3，g=9.8 m/s2，前飞速度为200 km/h。

盘旋机动、横滚机动、爬升机动和俯冲机动是直升机的4种典型机动飞行动作，分析其对尾斜轴临界转速的影响即可获得直升机各个转速运动分量对尾传动轴临界转速的影响规律。为分析直升机机动飞行时尾斜轴倾斜角对临界转速的影响规律和特点，文中首先分析尾水平轴的临界转速，再分析不同倾斜角的尾斜轴的临界转速。

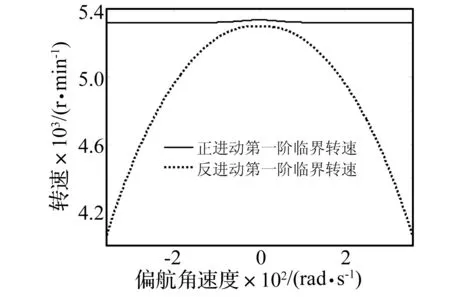
图2　定常盘旋机动飞行对尾水平轴第一阶临界转速的影响Fig.2 Influence of stationary hovering maneuvering flight on the first order critical speed of the horizontal tail drive shaft

虽然尾斜轴倾斜角较小时，临界转速与偏航角速度之间呈曲线关系，但是其曲率很小，故将其近似当作直线处理。φ=30°时可近似采用分段的直线方程表示为：

(5)

(6)

式中：npc2,30和nnc2,30分别表示倾斜角φ=30°的尾斜轴正、反进动第二阶临界转速，下标逗号之前的数字为临界转速的阶次，而逗号之后的数字为尾斜轴的倾斜角度。

倾斜角φ=45°和φ=60°时的近似表达式分别为

(7)

(8)

(9)

(10)

采用式(5)～(10)对直升机定常水平盘旋机动飞行时尾斜轴的第一阶临界转速进行估算，φ=30°时的最大误差不超过4%，φ=45°时的最大误差不超过1.2%，φ=60°时的最大误差不超过0.7%，故近似处理的结果在可接受范围。

由图4可知，水平轴正、反进动第二阶临界转速与偏航角速度之间的关系图均近似为开口向下的抛物线，对称轴为偏航角速度约等于0的竖轴。相对于第一阶临界转速，偏航角速度对反进动第二阶临界转速的影响变得很小，且偏航角速度对正、反进动临界转速的影响幅度差距大大缩小，两条曲线形状基本相同，说明临界转速的阶次越高，盘旋机动飞行对水平轴的影响越小。

(a) φ=30°(b) φ=45°(c) φ=60°图3 定常盘旋机动飞行对尾斜轴第一阶临界转速的影响Fig.3Influenceofstationaryhoveringmaneuveringflightonthefirstordercriticalspeedoftheobliquetaildriveshaft

图4　定常盘旋机动飞行对尾水平轴第二阶临界转速的影响Fig.4 Influence of stationary hovering maneuvering flight on the second order critical speed of the horizontal tail drive shaft

(11)

(12)

(13)

(14)

(15)

(16)

(a) φ=30°(b) φ=45°(c) φ=60°图5 定常盘旋机动飞行对尾斜轴第二阶临界转速的影响Fig.5Influenceofstationaryhoveringmaneuveringflightonthesecondordercriticalspeedoftheobliquetaildriveshaft

(17)

(18)

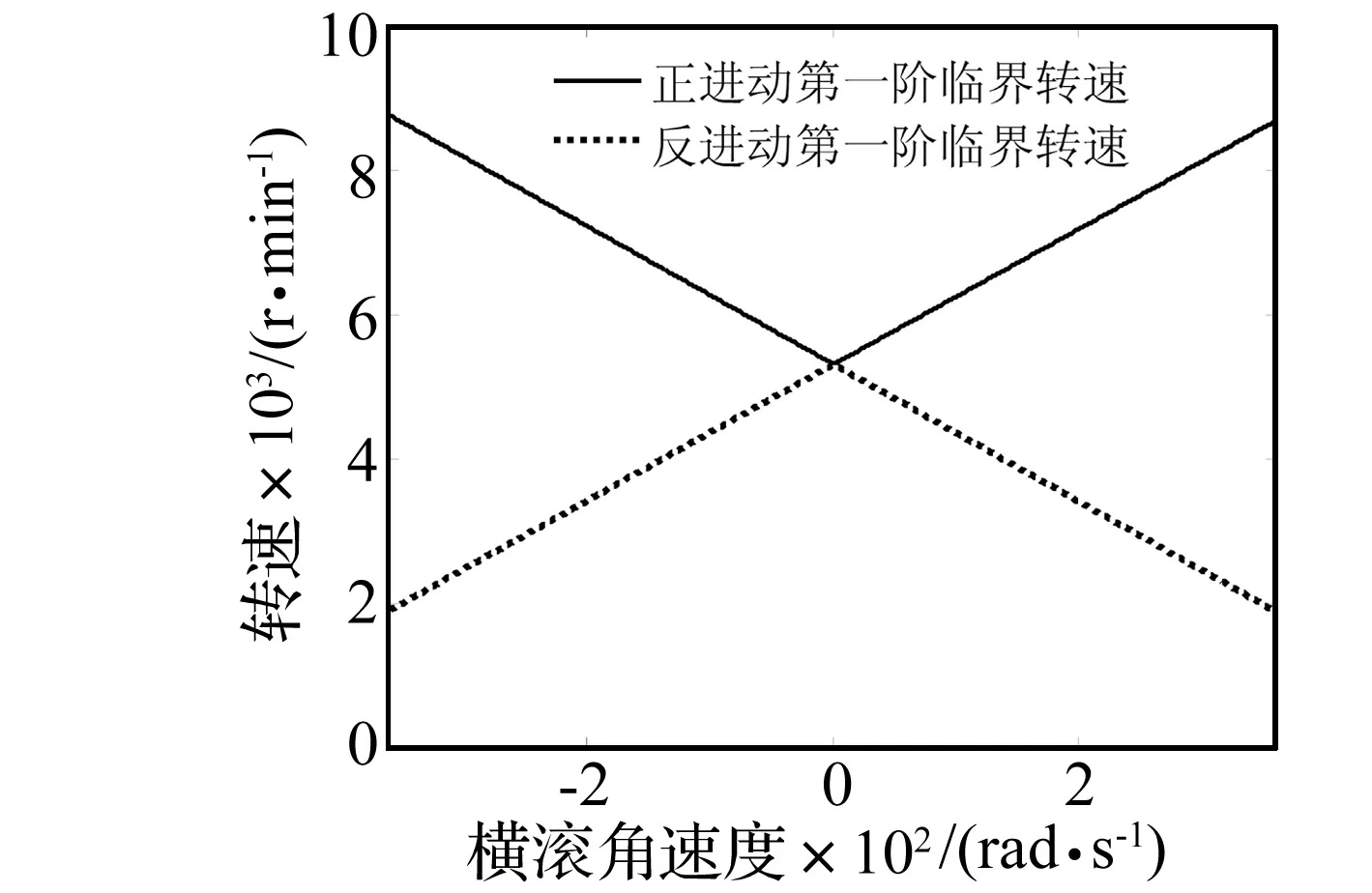
图6　定常横滚机动飞行对尾水平轴第一阶临界转速的影响Fig.6 Influence of stationary rolling maneuvering flight on the first order critical speed of the horizontal tail drive shaft

由图7可知，与直升机定常水平盘旋机动飞行的情况相反，直升机定常横滚机动飞行时，随着尾斜轴倾斜角φ的增大，临界转速与偏航角速度之间的关系逐渐由直线图形演变为曲线图形， 同一横滚角速度下的临界转速减小，对称轴位置向右偏移，其余特征与盘旋机动时类似。图7可用如下分段直线方程表示为：

(19)

(20)

(21)

(22)

(23)

(24)

其中：φ=60°时近似处理的误差最大，但是不超过1.7%。

(a) φ=30°(b) φ=45°(c) φ=60°图7 定常横滚机动飞行对尾斜轴第一阶临界转速的影响Fig.7Influenceofstationaryrollingmaneuveringflightonthefirstordercriticalspeedoftheobliquetaildriveshaft

(25)

(26)

图8　定常横滚机动飞行对尾水平轴第二阶临界转速的影响Fig.8 Influence of stationary rolling maneuvering flight on the second order critical speed of the horizontal tail drive shaft

图9表明，定常横滚机动飞行对尾斜轴第二阶临界转速的影响曲线呈线性特征， 对称轴对应的横滚角速度也是第一阶临界转速时的16倍左右，分别为35.15、43.05和60.85，其他特征与第一阶临界转速时的情况基本相同。第二阶临界转速与横滚角速度之间的关系可表示为：

(27)

(28)

(29)

(30)

(31)

(32)

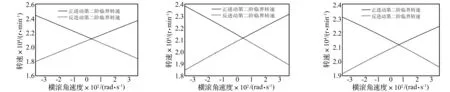
(a) φ=30°(b) φ=45°(c) φ=60°图9 定常横滚机动飞行对尾斜轴第二阶临界转速的影响Fig.9Influenceofstationaryrollingmaneuveringflightonthesecondordercriticalspeedoftheobliquetaildriveshaft

图10　非定常盘旋机动飞行对尾斜轴临界转速的影响 Fig.10 Influence of unsteady hovering maneuvering flight on the second order critical speed of the oblique tail drive shaft

3结论

本文分析了影响尾传动轴临界转速的直升机空间运动分量，通过几种典型的直升机机动飞行动作，获得了空间运动分量对尾传动轴临界转速的影响规律与特征，可得到如下结论：

(1) 影响尾传动轴临界转速的主要因素为直升机的转动角速度分量，角加速度运动分量影响很小，直升机的平动运动分量无影响。

(2) 偏航角速度仅对尾水平轴的反进动第一阶临界转速有较大影响，对正进动第一阶临界转速以及正、反进动第二阶临界转速影响均很小，且偏航角速度与尾水平轴临界转速近似呈抛物线关系。

(3) 偏航角速度对尾斜轴的临界转速影响较大，二者之间近似呈线性关系且为左右对称图形，随着尾斜轴倾斜角的增大，对称轴向左偏移，偏航角速度的影响幅度增大；第二阶临界值转速时的对称轴约为第一阶临界转速时的16倍。

(4) 俯仰角速度对尾传动轴临界转速的影响与偏航角速度相同。

(5) 横滚角速度与尾传动轴临界转速间近似呈线性关系，随尾斜轴倾斜角的增大，横滚角速度的影响幅度变小，对称轴向右偏移。

[ 1 ] Lopez C A, Wells V L. Dynamics and stability of an autorotating rotor/wing unmanned aircraft[J]. Journal of Guidance, Control, and Dynamics, 2004,27(2):258-270.

[ 2 ] Ananthan S, Leishman J G. Rotor wake aerodynamics in large amplitude maneuvering flight[J]. Journal of the American Helicopter Society, 2006, 51(3): 225-243.

[ 3 ] 祝长生, 陈拥军. 机动飞行时航空发动机转子系统的振动特性[J]. 航空学报, 2006, 27(5): 825-841.

ZHU Chang-sheng, CHEN Yong-jun. Vibration characteristics of aeroengine’s rotor system during maneuvering flight[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(5): 825-841.

[ 4 ] 祝长生, 陈拥军. 机动飞行时发动机转子系统动力学统一模型[J]. 航空动力学报, 2009, 24(2): 371-377.

ZHU Chang-sheng, CHEN Yong-jun. General dynamic model of aeroengine’s rotor system during maneuvering flight[J]. Journal of Aerospace Power, 2009, 24(2): 371-377.

[ 5 ] 林富生, 孟光. 飞行器机动飞行时发动机转子等变速运动的动力学特性研究[J]. 航空学报,2002,23(4):356-359.

LIN Fu-sheng, MENG Guang. Dynamics of a maneuvering rotor in constant acceleration and deceleration[J]. Acta Aeronautica et Ast Ronautica Sinica,2002,23(4):356-359.

[ 6 ] Lin Fu-sheng, Meng Guang. Study on the dynamics of a rotor in a maneuvering aircraft[J]. Journal of Vibration and Acoustics, 2003, 125(2): 324-327.

[ 7 ] 林富生, 孟光, E·韩.飞行器内裂纹转子系统的非线性动力学特性研究[J]. 应用数学和力学, 2004, 25(10): 1042-1052.

LIN Fu-sheng, MENG Guang, Eric Hahn. Nonlinear dynamics of a cracked rotor in a maneuvering aircraft[J].Applied Mathematics and Mechanics,2004,25(10):1042-1052.

[ 8 ] 林富生, 孟光. 飞行器内SFD-转子系统的动力学特性研究[J]. 振动工程学报, 2004, 17(4): 403-407.

LIN Fu-sheng, MENG Guang. Study on the dynamic characteristics of SFD-rotor system in aircrafts[J]. Journal of Vibration Engineering, 2004, 17(4): 403-407.

[ 9 ] 林富生, 孟光. 飞行器内碰摩转子模型的光滑处理及非线性研究[J]. 振动工程学报, 2004, 17(2): 184-188.

LIN Fu-sheng, MENG Guang. Study on the nonlinear characteristics of a maneuvering rotor system with smoothly treated step impact-rubbing forces[J]. Journal of Vibration Engineering, 2004, 17(2): 184-188.

[10] 徐敏, 廖明夫, 刘启洲. 机动飞行条件下双盘悬臂转子的振动特性[J]. 航空动力学报, 2002, 17(1): 105-109.

XU Min, LIAO Ming-fu, LIU Qi-zhou. The vibration performance of the double-disk cantilever rotor in flight mission[J]. Journal of Aerospace Power,2002,17(1):105-109.

[11] 徐敏, 廖明夫. 机动飞行条件下带挤压油膜阻尼器的Jeffcott 转子的振动特性[J]. 航空动力学报, 2003, 18(3): 394-401.

XU Min, LIAO Ming-fu. The vibration performance of the Jeffcott rotor system with SFD in maneuver flight[J]. Journal of Aerospace Power, 2003, 18(3): 394-401.

[12] 顾致平, 于渊博. 飞机水平盘旋下弹性支承转子的特性研究[J]. 西安工业大学学报, 2008, 28(6): 589-593.

GU Zhi-ping, YU Yuan-bo. Investigation of rotor characteristics with elastic support inaircraft of horizontal circling[J]. Journal of Xi’an Technological University, 2008, 28(6): 589-593.

[13] 杨永锋, 任兴民, 秦卫阳. 俯冲拉起下裂纹转子的非线性[J]. 振动与冲击, 2007, 26(4): 21-24.

YANG Yong-feng, REN Xing-min, QIN Wei-yang. Nonlinear response analysis of a cracked jeffcott rotor in action of dive-hike[J]. Journal of Vibration and Shock, 2007, 26(4): 21-24.

[14] 杨永锋, 任兴民, 秦卫阳. 水平盘旋下裂纹转子的非线性响应[J]. 航空动力学报, 2007, 22(6): 1007-1012.

YANG Yong-feng, REN Xing-min, QIN Wei-yang. Study of nonlinear response of cracked Jeffcott rotor in hovering state[J]. Journal of Aerospace Power,2007,22(6):1007-1012.

[15] 许兆棠. 多支点传动轴动力学的研究[D]. 南京：南京航空航天大学, 2006.

[16] 倪德, 朱如鹏, 靳广虎, 等. 机动飞行时直升机尾传动轴的横向振动建模与特性[J]. 振动与冲击, 2014, 33(7): 215-220.

NI De, ZHU Ru-peng, JIN Guang-hu, et al. Modeling and characteristics of bending vibration for helicopter tail drive shaft during maneuver flight[J]. Journal of Vibration and Shock, 2014, 33(7): 215-220.

Influence of a helicopter’s maneuvering flight on critical speed of its tail drive shaft

LU Feng-xia1, ZHU Ru-peng1, NI De2

(1. College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;2. China Aviation Powerplant Research Institute, Aviation Industry Corporation of China, Zhuzhou 412002, China)

All translational motion components of a helicopter and position parameters of its tail drive shaft do not affect critical speeds of its tail drive shaft, and only rotating motion components of the helicopter affect critical speeds of its tail drive shaft. The influences of rotating motion components of a helicopter on critical speeds of its tail drive shaft were analyzed. The results showed that the yaw angular velocity versus the critical speed of the horizontal drive shaft reveals a relation of parabola, while the yaw angular velocity versus the critical speed of the oblique tail drive shaft is a linear relation and the relation curve is symmetrical; the symmetry axis offsets to the left with increase in the inclination angle of the oblique tail drive shaft; the influence of the pitching angular velocity on critical speeds of the tail drive shaft is the same as that of the yaw angular velocity; the relations’ between the rolling angular velocity and critical speeds of the horizontal drive shaft and the oblique tail drive shaft are a linear relation, and the symmetry axis offsets to the right with increase in the inclination angle of the oblique tail drive shaft; the angular velocity corresponding to the symmetric axis of the second-order critical speed curve of the drive shaft is about 16 times of the first-order critical speed.

helicopter; tail drive shaft; maneuvering flight; bending vibration; critical speed

10.13465/j.cnki.jvs.2016.11.017

国家自然科学基金(51375226)；国家自然科学基金(51475226)

2015-01-16修改稿收到日期：2015-06-04

陆凤霞 女，博士生, 副教授,硕士生导师，1972年4月生

朱如鹏 男，博士，教授,博士生导师，1959年9月生

TH113.2；TH113.1

A