EMD马氏距离与SOM神经网络在故障诊断中的应用研究

姚海妮，王　珍，邱立鹏，陈建国，杨　铎

（大连大学 机械工程学院，辽宁 大连 116622）



EMD马氏距离与SOM神经网络在故障诊断中的应用研究

姚海妮，王珍，邱立鹏，陈建国，杨铎

（大连大学 机械工程学院，辽宁 大连 116622）

摘要：为实现对微弱动态响应的准确辨识及故障状态的早期诊断，提出EMD马氏距离与SOM神经网络的故障诊断方法，该方法首先对原始振动信号进行粒子滤波，提高信噪比，然后对其进行EMD分解，并对分解后的各模式分量进行分析，获得相关特征值组成特征向量，并求原始信号特征向量，为了选取能代表信号特征的模式分量，求各模式分量与原信号特征向量的马氏距离，将最优模式分量输入训练好的SOM神经网络，对故障分类，以轴承诊断为应用实例结果表明该方法切实有效。

关键词：振动与波；粒子滤波；EMD；马氏距离；SOM神经网络；故障诊断

故障诊断主要研究如何对系统中出现的故障进行检测、分离和辨识。目前，基于模糊理论的诊断方法、专家系统故障诊断方法、小波分析法以及一些常规故障诊断方法的应用具有一定的局限性。文献[1]提出EMD能量熵支持向量机故障诊断方法，由于背景噪声对信号的干扰和支持向量机核函数构造及惩罚因子设置的准确率问题，该方法并不很理想。EMD方法能够将信号分解成一些能够反映出信号的特征尺度的基本模式分量，具有很强的自适应性；马氏距离是计算两个未知样本集相似度的方法，利用它可以选取与原信号相关性大的分量，从而剔除无关分量，提高诊断效率；SOM神经网络是一种结构简单，自适应分类能力比较强的自组织特征映射网络，经PSO优化的SOM神经网络可以高效的对故障分类；将EMD马氏距离和神经网络结合可以充分发挥各自优势，加快训练速度，辨别故障类型、缩小故障范围，并对故障准确的定位。

EMD马氏距离与神经网络的诊断方法，其自学与数据处理能力强，适合处理复杂机械设备的轴承故障、齿轮故障、转子等故障诊断问题。

1　基本原理

1.1 EMD方法原理

EMD分解就是将信号分解为多个能表征模糊频带和顺时频率双重信息的IMF分量。固有模式分量两零点间没有其他叠加波。故原信号经EMD分解后，可表示成为固有模式函数，rn(t)为趋势项，因此EMD分解完全由信号自身的变化决定，是一种自适应信号分解方法。

1.2马氏距离方法原理

马氏距离是通过计算数据样本集之间的协方差距离有效度量两个未知样本集相似度，样本y和样本集 m×n矩阵x之间的马氏距离定义为为样本向量的维数，n为样本的数量，为矩阵x的重心，定义为cx为矩阵x的协方差矩阵，定义为

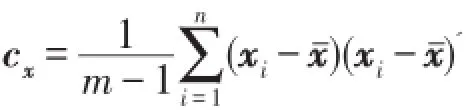
马氏距离越小表明两个样本之间的相似度越大，它不受量纲的影响，而且马氏距离能考虑到各种特性之间的联系，可以排除变量之间相关性的干扰。

1.3 SOM神经网络原理

SOM网络用于对输入变量进行区域分类，可以研究输入变量的分布特性和拓扑结构。基本原理：SOM神经网络是一种无监督聚类算法，任意维输入模式在它的作用下形成一维或者二维平面阵列，然后被映射成一维或二维离散图形，最后在竞争层输出结果，并且输入模式的特征结构维持不变。输入层用于接收输入模式，映射层用于显示输出模式，映射层中的神经元和输入层神经元实现全连接，其内部的神经元则相互连接，共同完成模式聚类功能。

2　方法实现

样本信号与待测信号来自型号为6205-2RS JEM SKF，深沟球轴承，转速为1 722 r/min，采样频率为12 kHz，分析点数为2 048。为了提高信号的信噪比，先利用粒子滤波法滤除背景噪声，然后对其进行EMD分解并对分解后的各模式分量进行分析，获得相关特征值组成特征向量。并求未分解的原始信号的特征向量，求各IMF特征向量与原始信号特征向量的马氏距离，找到与原始信号马氏距离小的那些IMF分量，作为待诊信号。输入训练好的并经PSO算法优化的SOM神经网络中，对故障分类并输出诊断结果，方法实现如图1。

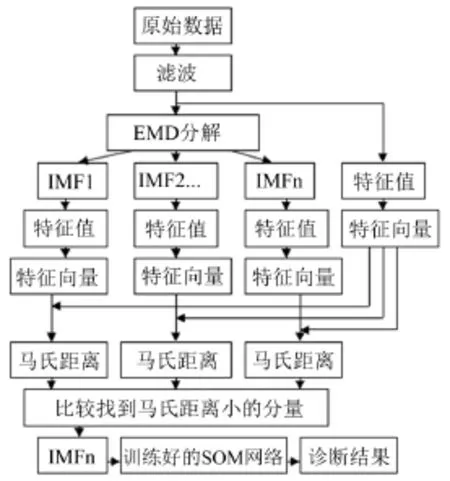
图1　EMD马氏距离神经网络方法实现

3　应用实例

3.1滤波

为提高信噪比，将原始信号采用粒子滤波法滤除背景噪声，滤波前后的曲线如图2所示。

3.2 EMD分解

将滤波后的原始信号进行分析得时域、频域曲线如图3所示。对EMD分解后的IMF分量进行分析，提取各自的特征值，将各特征值组成特征向量，作为计算马氏距离的输入量，EMD分解曲线如图4所示。

3.3马氏距离归一化处理

图2　滤波前信号图(a)、滤波后信号曲线图(b)

以时域、频域特征向量为参数计算各个分量与原始信号的马氏距离，马氏距离较大时，表明两信号相似性小，故剔除与原始信号马氏距离大的虚假分量，保留最能代表信号特征的分量作为待诊信号。为了用图形更直观表示，对马氏距离进行归一化处理，结果如图5所示。

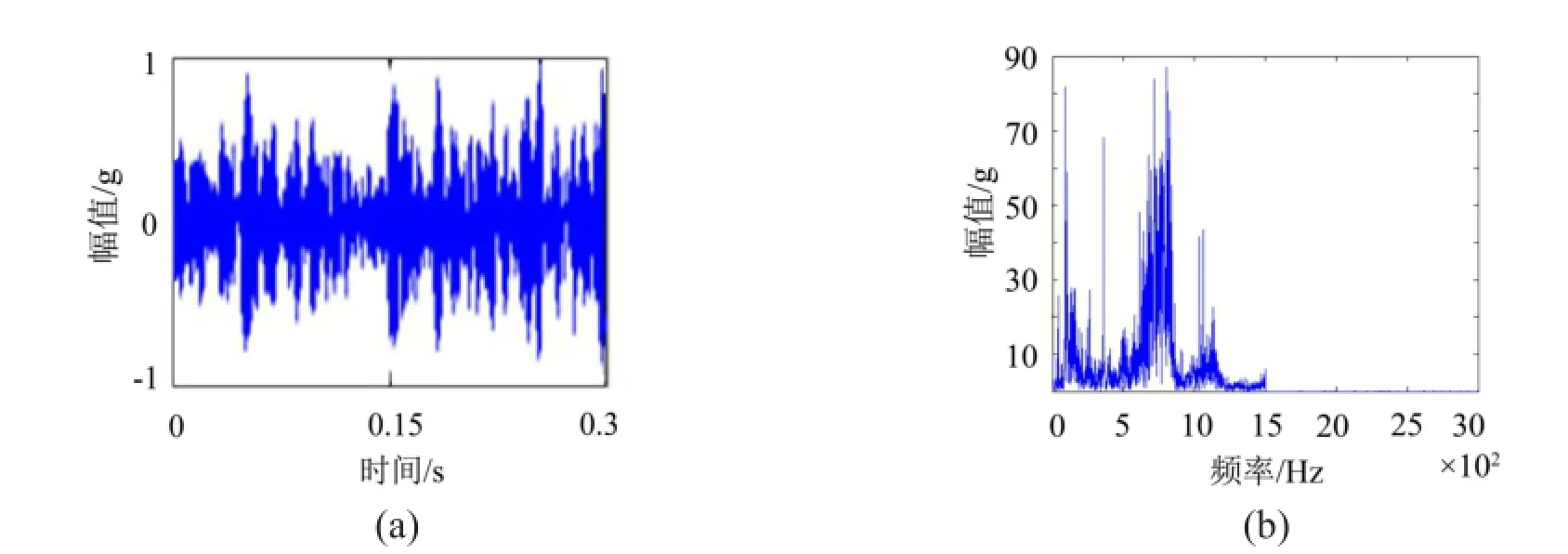
图3　原信号时域图(a)、频域曲线图(b)

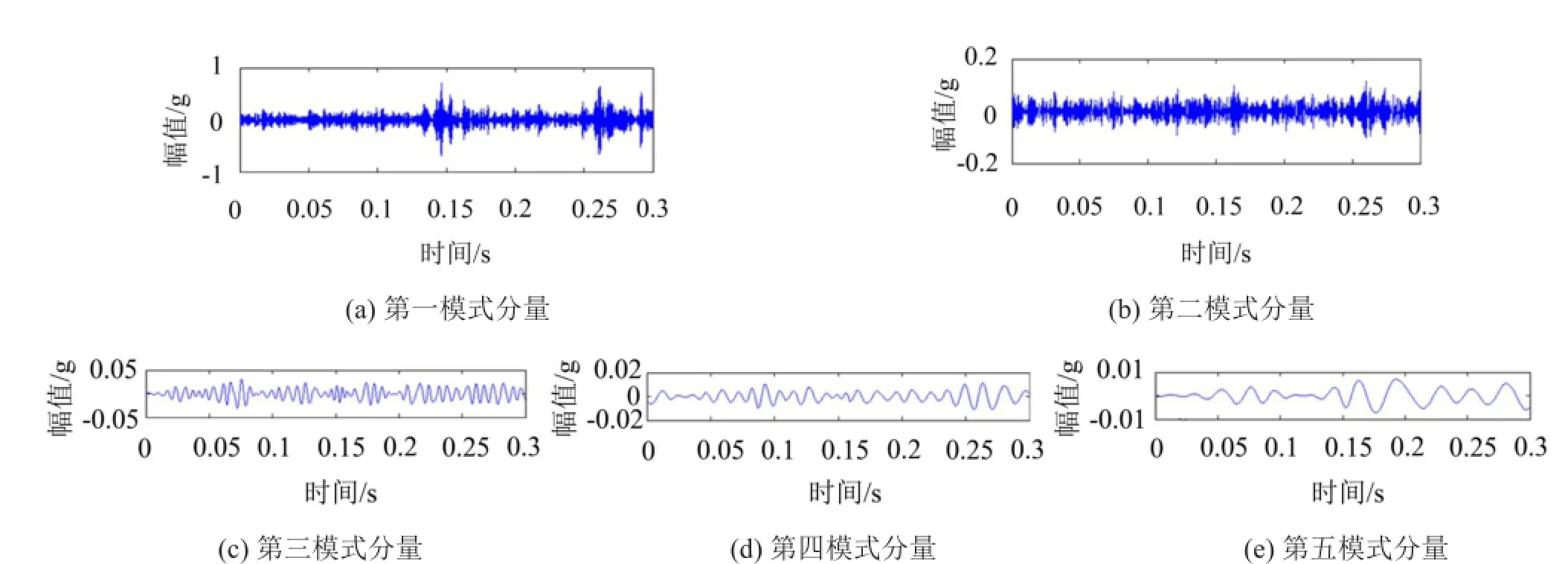
图4　EMD分解曲线

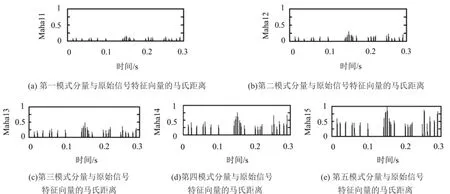
图5　各IMF分量与原始信号特征向量的马氏距离

3.4 SOM神经网络训练

首先将去噪后的典型故障样本EMD分解，将与原信号特征向量马氏距离小的IMF分量输入SOM神经网络进行学习。SOM神经网络模型建立流程如图6。

图6　SOM神经网络模型建立的流程图

选择峰值指数、波形指数、裕度指数和峭度等4种无量纲参数组成表征滚动轴承运行状态的特征向量，并作为SOM神经网络的输入参数，根据样本故障类型及特征参数，综合确定SOM网络的输入由40个神经元组成。创建网络的竞争层为5×8的结构。已获取的该轴承归一化处理的故障数据典型训练样本见表1。根据SOM网络的自组织特征映射功能，将所有这些典型故障样本输入到SOM神经网络中去训练，反复调整权值，训练完成后在输出层的映射结果用矩阵表示，SOM网络聚类矩阵图见图7。

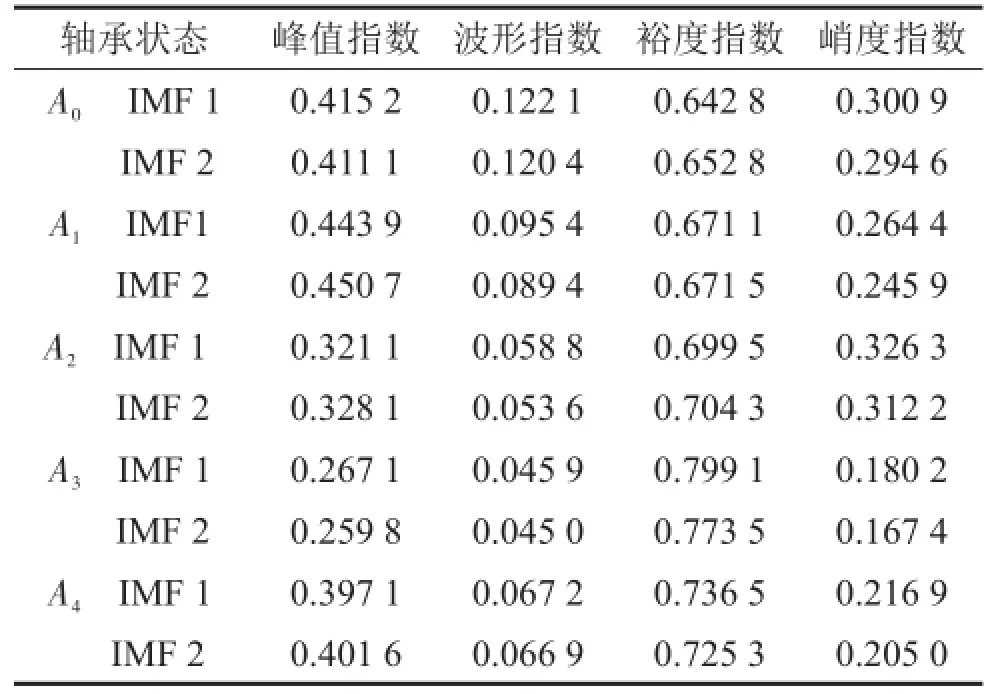
表1　四种故障特征值的学习样本表

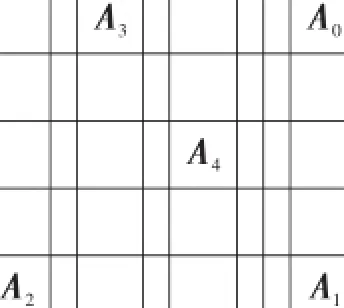
图7　训练后SOM网络聚类矩阵图

选择典型故障样本的1组IMF分量检测训练好的网络可靠性，选取数据为IMF=[0.447 2、0.090 1、 0.667 5、0.221 2]，输出结果为A1，即激发了SOM网络的A1神经元，属于外圈故障，诊断准确。

3.5故障分类及诊断结果

通过计算各IMF分量与原始信号特征向量的马氏距离剔除干扰信号，得到5组待测信号，分别记作m1、m2、m3、m4、m5，为滚动体故障、外圈故障、内圈故障、滚动体故障、正常。用PSO算法优化SOM神经网络，PSO算法的参数设为：c1=c2=1.6，ω随迭代次数线性地从0.9减小为0.3。迭代次数为190次。将待诊分量输入到经PSO优化好的SOM神经中，输出结果如图8所示。

图8　网络诊断故障矩阵图

由图8可以看出，经PSO优化的SOM神经网络聚类效果明显，m1被很好的分类到第2类故障模式，即滚动体故障，m2被分类到第1类故障为外圈故障，m3被分类到第4类故障，即内圈故障，m4被分类到第3类故障为保持架故障。m5为正常。所有的样本均可被分类为两种模式，即正常状态和故障状态，所有数据均被成功分类，最后检验SOM神经网络百分误差大小

Yci、Yi为计算值和实测值，为实测值的平均值，n为样本数。以训练次数为横坐标，百分误差为纵坐标，结果如图9所示。

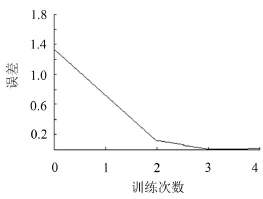
图9　误差与训练次数的关系

图9中显示训练到4次(1次=100步)时，误差趋于0，即当训练到大于400步的时候，误差已经较小，已无需继续训练。

4结　语

EMD马氏距离神经网络的故障诊断方法首先利用EMD对测量数据分解成具有不同特征尺度的分量，然后计算各分量与原始信号的马氏距离，剔除马氏距离大的干扰分量，简化输入变量，缩小SOM神经网络的搜索空间，提高了故障诊断精度。利用典型故障样本训练SOM神经网络，再将含有故障特征的IMF分量输入到训练好的SOM神经网络中，应用实例表明该方法能高效精确的进行故障分类并且具有良好的诊断精度和较强的适应能力。此外，该方法还可用于其他机械设备的故障诊断中。

参考文献：

[1]张超，陈建军，郭迅.基于EMD能量熵和支持向量机的齿轮故障诊断方法[J].振动与冲击，2010，29(10)：216-220.

[2]张清华，邵龙秋，李红芳，等.基于无量纲指标的旋转机械并发故障诊断技术[J].华中科技大学学报(自然科学版)，2009，8(37)：156-159.

[3]马继昌，司景萍，牛嘉骅，等.基于自适应模糊神经网络的发动机故障诊断[J].噪声与振动控制，2015，35(2)：165-169.

[4]王珍，郭方，江亲瑜.EMD的Lab VIEW实现及其在滚动轴承故障诊断中的应用[J].噪声与振动控制，2009，29 (4)：54-57.

[5]万书亭，佟海侠，董炳辉.基于最小二乘支持向量机的滚动轴承故障诊断[J].振动、测试与诊断，2010，30（2）：149-152.

[6]李辉，郑海起，唐力伟.基于改进双树复小波变换的轴承多故障诊断[J].振动、测试与诊断，2013，33(1)：53-59.

[7]Eftekharnejad B,Carrasco M R,Charnley B,et al.The application of spectral kurtosis on acoustic emission and vibrationsfromadefectivebearing[J].Mechaniacl Systems and Signal Processing,2011,25(6);266-284.

辽宁省教育厅一般项目(L2012446)

究方向：故障诊断。

E-mail:1403201470@qq.com

研究方向：故障诊断与振动噪声控制。

中图分类号：TH133.3；TH165+.3

文献标识码：A

DOI编码：10.3969/j.issn.1006-1335.2016.01.030

文章编号：1006-1355(2016)01-0138-04+162

收稿日期：2015-06-30

基金项目：国家自然科学基金(51405153)；

作者简介：姚海妮(1989-)，女，山东烟台市人，硕士生，主要研

通讯作者：王珍(1971-)，男，江苏丰县人，博士后，教授，主要

Application of EMD Mahalano-bis Distance and SOM Neural Network in Fault Diagnosis

YAO Hai-ni,WANGZhen,QIU Li-peng,CHEN Jian-guo,YANGDuo

(College of Mechanical Engineering,Dalian University,Dalian 116622,Liaoning China)

Abstract:To achieve accuracy identification of weak dynamic response and early fault diagnosis,a fault diagnosis method based on EMD Mahalano-Bis distance and SOM neural network was proposed.First of all,to improve the signal-tonoise ratio,particle filtering was conducted to the original signals of vibration.Then,the signals were decomposed by the EMD.Each intrinsic mode function was analyzed to obtain the eigenvectors which include their corresponding eigenvalues. And the eigenvectors of the original signals were found.In order to select the intrinsic mode function which can represent the signal characteristics,the Mahalano-Bis distance between the intrinsic mode functions and the eigenvectors of the original signals was calculated.The best intrinsic mode function was chosen and input to the well-trained self-organizing feature map(SOM)neural network.Finally,the faults were classified.The application examples of bearing fault diagnosis show the effectiveness of this method.

Key words:vibration and wave;particle filter;empirical mode decomposition(EMD);Mahalano-bis distance method; self-organizing feature map(SOM)network;fault diagnosis