基于灰色关联度的深切口椭圆柔性铰链稳健性优化设计*

伍建军，黄裕林，谢周伟，吴小明

( 江西理工大学 机电工程学院，江西 赣州　341000)



基于灰色关联度的深切口椭圆柔性铰链稳健性优化设计*

伍建军，黄裕林，谢周伟，吴小明

( 江西理工大学 机电工程学院，江西 赣州341000)

摘要：针对深切口椭圆柔性铰链设计结构参数存在不稳定的问题，建立了深切口椭圆柔性铰链的柔度运动模型，基于该模型提出了一种基于灰色关联度的稳健设计新方法。该方法是通过描述深切口椭圆柔性铰链柔度的一个关联度序列，分析铰链的柔度线性关系，利用灰色关联度评估铰链的柔度的关联程度，然后根据方差分析表中的方差波动百分比对每个因子的进行排序，得到一个关联度最大的稳健性因子水平组合。结果表明该方法可以为柔性铰链在可靠性稳健设计方面提供一种新的解决途径。

关键词：深切口椭圆柔性铰链；灰色关联度；稳健设计

0引言

柔性铰链是一种无机械摩擦、无间隙、运动灵敏度高和稳定性好的机构。随着微机电系统技术的迅速发展，而被广泛地应用于精密定位、微电子工程和生物工程等领域[1-2]。但由于柔性铰链受到结构参数可控因子和噪声因子的影响，使其机构的性能产生波动，极大的影响了铰链柔度的精度。故为提高柔性铰链的柔度精度如何寻找出一个最优可控因子水平组合使铰链柔度对噪声因子具有良好的抗干扰性，已成为柔顺机构的研究热点。

国内外学者对柔顺铰链主要是研究功能性拓扑优化，而针对功能的抗干扰能力、稳健性优化设计方面相关文献较少。文献[3]提出了一种平面两自由度全柔顺微运动并联机构的拓扑优化设计方法，该方法首先分析了平面两自由度全柔顺并联机构的微运动学，然后在此基础上建立了该机构的拓扑优化模型，并利用OC算法对所建立的模型进行求解，最后运用有限元软件对所建立的三维模型进行仿真，结果表明该方法的有效性；文献[4] 针对传统方法在拓扑优化中会出现局部应变集中的缺陷，提出了一种基于整体有效应变的柔顺机构多目标拓扑优化方法，该方法能够减少基于传统优化方法的结构中的局部大应变，从而有效提升柔顺机构的可靠性；文献[5]提出了柔顺机构多目标拓扑优化方法，该方法以应变能最小化和互应变能最大化为目标，以结构体积为约束，采用标准化方法定义多目标拓扑优化的目标函数，消除不同性质目标函数在数量级上的差异。上述研究主要是对柔性铰链进行拓扑优化，并没有考虑铰链柔度精度稳健优化设计的问题，但在实际应用中柔度的精度是必须被考虑的。

为此，本文以深切椭圆柔性铰链为研究对象，针对该机构设计中结构参数存在柔度不稳定的问题，建立了深切口椭圆柔性铰链的柔度运动模型，基于该模型提出了一种基于灰色关联度的稳健设计方法来破解微纳柔性铰链设计不稳定的难题，最终得到稳健性设计方案，为柔性机构的稳健设计提供了一定的借鉴和依据。

1深切口椭圆柔性铰链柔度运动模型

深切口椭圆柔性铰链见图1。a、b分别为椭圆切口的长轴半径与短轴半径，柔性铰链的高度、宽度和最小切割厚度分别为h、w、t。

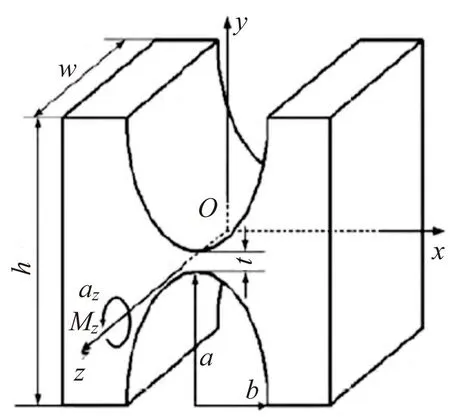
图1　深切口椭圆柔性铰链

由于深切口椭圆柔性铰链运动的输入轴是Z轴，且绕Z轴旋转的角位移是该机构运动精度和性能的关键因素，故仅考虑对该机构在受旋转力矩Mz引起的Z轴旋转的角位移进行分析[6-8]。经查阅参考相关文献，本文在对柔性铰链施加旋转力矩Mz作用下，其柔度计算公式为[9]：

(1)

式中：E—弹性模量，单位为GPa；w(mm)—铰链宽度；t(mm)—铰链厚度；a(mm)—铰链长轴半径；

在工程实践中，深切椭圆柔性铰链由于受到不确定性因素的影响，难以得到一个稳定性较好的优化水平组合。故如何采用科学合理的方法来确定水平组合一直是柔顺机构稳健设计的难题之一。针对这一问题，拟采用灰色关联度进行更加精确的稳健优化。

2基于灰色关联度分析法稳健设计模型的建立

灰色关联度分析法是根据序列的几何形状相似程度来判断序列之间是否紧密联系[10]。若果几何形状的波动趋势接近，甚至相同，则表明相应序列之间具有较强的关联性；反之有较弱的关联性。灰色关联度定义如下：

γ(R0(k),Xi(k))=

(2)

(3)

式中：i=1,2,…,m；k=1,2,…,n；ξ—分辨系数，一般取ξ=0.5。R0=(R0(1),R0(2),…,R0(n))为参考序列，Xi=(Xi(1),Xi(2),…,Xi(n))为比较序列。

γ(R0(k),Xi(k))是R0与Xi第k个数据对应的关联系数，γ(R0,Xi)是R0与Xi的关联度。

为此构建基于灰色关联度稳健设计模型具体步骤如下所示：

(1)规范化处理。根据原始的试验数据，针对不同类型的质量特性，采用不同的规范化进行处理，其过程如下：

①望小特性:

(4)

②望目特性:

(5)

③望大特性:

(6)

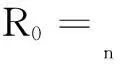
(3)计算X*与R0的差矩阵T的元素。

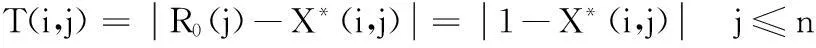
(7)

并求出差矩阵T的元素中的最大值M以及最小值m。

(4)根据公式(2)计算出关联系数矩阵R。

(5)根据公式(3)计算出关联度序列r，其值为γ状态下的加权平均值，而后将r填入正交表中进行方差分析。对方差分析表中各因素的百分比进行排序，然后根据因子水平J1,J2,…,Js(s为因子水平数)的最大值，得到稳健性因子水平组合。

有了上述灰色关联度稳健设计模型，柔顺结构的稳健优化设计就可以科学测度并进行优化了。接下来以实例进行说明。

3实例

考虑如图 1 所示深切口椭圆柔性铰链结构，弹性模量E=71GPa，铰链宽度w∈[0.5，1.5]mm，切口长轴半径a∈[1，3]mm，最小切割厚度t∈[0.3，0.5]mm。对于误差因子，选定w的误差为±4%、a的误差为±4%、t的误差为±4%。需得到柔性铰链几何尺寸，使得柔性铰链在受旋转力矩Mz引起的Z轴旋转是稳健的，绕Z轴转动的柔度最大化。

按照微动平台柔性的实际工程背景，选取3个具有代表性的a、t、w可控因子，取值水平可控因子水平配置见表铰链1。

表1　可控因子水平配置　(单位：mm)

在确定柔性铰链结构的可控因子水平配置后，选用L9正交表作为可控因子表。用综合误差法，对内表中的每行可控因子选最不利状况下各进行1次试验，其试验数据见表2。

表2　试验数据

续表

参数值(mm)柔度值(10-3μm/N)atwC1C2关联度20.41.51.3101.6650.371420.50.52.2452.8540.429730.31.53.3034.2000.522530.40.55.3247.1330.939530.511.3791.7530.3752

根据灰色关联度稳健设计模型可以得到如下结果：

1)规范化处理。由于该柔度为望大特性，所以根据公式(6)对C1和C2试验数据进行规范化得：

2)选取参考序列R0。因为规范化后的数据为望大特性，且输出为两个，所以取R0=(1,1)为参考序列。

3)计算X*与R0的差矩阵T的元素。由公式(7)可得差矩阵T：

由差矩阵T得元素中的最大值M=1.0000以及最小值m=0.0000。

4)由公式(2)计算出关联系数矩阵R：

5)假设C1和C2的权重相同，据公式(3)可以得到每组试验组合的关联度序列r:

将其关联度序列填入表2，通过Minitab进行方差分析，结果见表3。

表3　方差分析表

由表3可得，各因子波动比例排序次序为铰链宽度w>最小切割厚度t>切口长轴半径a。w的波动百分比较t与a百分比之和还大，故可知w为显著因子，t和a为次要因子。由J1，J2，J3中的最大值可以得到各因子的稳健水平组合为a3t1w1。

4稳健设计结果分析

为验证该方法的有效性，根据所得深切口椭圆柔性铰链最佳设计方案，计算分析柔度在显著影响因子w的最佳取值水平区域的精度，若柔度变化波动小，则表明结果稳健，反之不稳健。因w取值已达到临界最小值，故令w因子取值均比最优取值分别增大1%、2%、3%、4%，此时，柔度变化结果如表4 所示(↑表示增大，↓表示减小)。

表4　柔度与因子变化表　(单位：%)

由表4精度分析可以看出w因子在误差允许范围内变化时，柔度变化波动小于5%，深切口椭圆柔性铰链柔度在显著因子w的最佳设计区域具有较高的精度，表明该方法是有效的。

同时为进一步验证该方法的稳健性，将深切口椭圆柔性铰链最佳设计方案a3t1w1，在最不利状况下各进行1次试验，柔度值分别为7.07×10-3μm/N、9.00×10-3μm/N，并根据柔度的质量特性计算出信噪比[11]，同时与文献[12]方法进行比较，见表5。由表5可知，文献[12]方法得到的水平组合为a3t2w1，而本文方法水平组合为a3t1w1，本文方法的信噪比相比文献[12]增加了2.3dB，相当于柔度精度的稳健性提高了约15%，表明该方法可以有效地解决微机构设计中存在柔度不稳定的问题，为微机构领域可靠性稳健设计提供理论依据。

表5　结果对比分析表　(单位：dB)

5结论

针对该柔性铰链设计中结构参数不稳定的问题，以深切口椭圆柔性铰链为研究对象，建立深切口椭圆柔性铰链的柔度运动模型，基于该模型提出了一种基于灰色关联度的稳健设计方法，通过一个描述深切口椭圆柔性铰链的柔度的关联度序列，分析铰链的柔度线性关系，利用灰色关联度评估铰链的柔度的关联程度，并根据方差分析表中的方差波动百分比对每个因子的进行排序，得到一个关联度最大的稳健性因子水平组合。采用所提方法进行了精度分析，同时将所提方法与文献方法进行了对比分析，结果说明所提方法可以有效地解决微机构设计中存在不稳定的问题，为满足微纳柔性铰链高、精、尖的可靠性与精度方面严苛要求的优化设计方案的甄选提供了一种新的解决途径，有较大的推广实用价值。

[参考文献]

[1]ZHANGYan-jun.Performanceanalysisof2Djiggleplatformbasedonansys[J].MachineTool&Hydraulics,2013,41(9):154-162.

[2]WANGKai-bo,XUYing,SHAOMeng,etal.Stabilityanalysisoftwotypesoftypicalflexurehingeguidedmechanism[J].NanotechnologyandPrecisionEngineering, 2014,12(2):97-106.

[3] 朱大昌,宋马军,李雅琼.平面两自由度全柔顺微运动并联机构的拓扑优化设计[J].机械设计,2015,32(10):15-18.

[4] 孙楷,薄瑞峰,路建鹏,等.基于整体应变的柔顺机构多目标拓扑优化设计[J].工程设计学报,2015,22(6):575-580.

[5] 倪昀,占金青,朱大昌.基于混合元胞自动机的柔顺机构多目标拓扑优化方法[J].中国机械工程,2012,23(7):860-863.

[6]QINYD,BINJANS,ZHANGDW,etal.Compliancemodelingandanalysisofstaticallyindeterminatesymmetricflexurestructures[J].PrecisionEngineering,2013,37(2):415-424.

[7] 赵磊,巩岩,赵阳.光刻投影物镜中的透镜X-Y柔性微动调整机构[J].光学精密工程,2013,21(6):1425-1433.

[8]WENDYFF,MOISESRL,OLEGSE,etal.Combinedapplicationofpowerspectrumcentroidandsupportvectormachinesformeasurementimprovementinopticalscanningsystems[J].SignalProcessing,2014,98(5):37-51.

[9] 陈贵敏,韩琪.深切口椭圆柔性铰链[J].光学精密工程,2009,17(3):570-575.

[10] 刘思峰，党耀国，方志耕，等. 灰色系统理论及其应用[M]. 北京：科学出版社，2010.

[11] 刘国兴，任世彬.田口方法与稳健性设计[J].电工电气，2010(10):53-57.

[12] 陈文彬，李淑娟，陈文革，等.基于RSM的Al2O3陶瓷膏体配方优化[J].材料科学与工艺，2015，23(2)：13-18.

(编辑李秀敏)

文章编号：1001-2265(2016)07-0011-04

DOI:10.13462/j.cnki.mmtamt.2016.07.004

收稿日期：2015-12-20；修回日期：2016-01-19

*基金项目：国家自然科学基金(51365015)；省科技厅科技项目资助(20142BBE50058)

作者简介：伍建军(1974—)，男，四川南充人，江西理工大学副教授，博士，研究方向为工业工程与机械、质量与可靠性，(E-mail)1129728208@qq.com。

中图分类号：TH16；TG506

文献标识码：A

Robust Optimal Design of Deep-notch Elliptical Flexure Hinge Based on Grey Correlation Degree

WU Jian-jun,HUANG Yu-lin,XIE Zhou-wei,WU Xiao-ming

(School of Mechanical and Electrical Engineering, Jiangxi University of Science and Technology,Ganzhou Jiangxi 341000, China)

Abstract：In view of deep-notch elliptical flexure hinge design that exists the problem of unstable,the establishment of deep notch elliptical flexure hinge motion model compliance,on the basis of the model, a new method of robust design based on grey correlation degree is proposed.This method is through a correlation sequence describing the deep notch elliptical flexure hinges,analysis of hinge flexibility of linear relationship,using grey correlation evaluation hinges the correlation degree of flexibility,then according to the variance fluctuation percentage of variance analysis table for sorting to each factor,a correlation of the maximum level of robustness factor is obtained.The results show that the method can provide a new solution for the reliability robust design of the flexible hinge.

Key words：deep-notch elliptical flexure hinge;grey correlation degree;robust design