伴有参与性介质的开口系统传热研究

夏　宇,仇性启,惠媛媛

(中国石油大学(华东) 化学工程学院,山东 青岛 266580)



伴有参与性介质的开口系统传热研究

夏宇,仇性启,惠媛媛

(中国石油大学(华东) 化学工程学院,山东 青岛 266580)

摘要:基于耗散极值原理,综合考虑高温烟气和高温固体壁面间的辐射对流耦合传热过程,推导出适用于伴有参与性介质的等温漫射灰体开口系统传热分析的平衡方程,并验证该方程的正确性,拓展了理论应用范围.将该方程应用于现代燃烧单元结构分析,通过Matlab软件编程,理论计算得到再辐射壁面开口宽度、燃烧筒到烟气出口垂直距离、炉灶开口宽度等参数对热效率、锅底和燃烧筒传热量、再辐射壁面温度的影响规律,指出炉灶开口宽度是影响现代燃烧单元传热性能的关键结构参数.

关键词：耗散；等温漫射；传热；现代燃烧单元

1模型建立与方程推导

对于伴有参与性介质的等温漫射灰体开口系统(本文统称为“系统” )中任一表面k ,能量守恒方程可以表示为

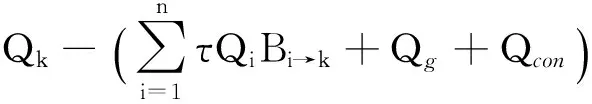
(1)

式中：Qnet-k为表面k的净传热量；τ为表面辐射热能通过烟气时的衰减系数[17]；Qi为表面i 发射的热能；Bi→k为吸收系数,表示由表面i发射而被表面k吸收的热能所占份额；Qg为烟气对表面k的辐射传热量；Qcon为采用牛顿冷却定律计算烟气与壁面间的对流传热量.等式右边第二项表示由表面i发射而被气体吸收后透射到表面k的能量.

式(1)为系统能量平衡方程.可以看出方程形式与一般能量守恒方程一致[17].规定系统表面发射能量为正,吸收能量为负.当表面k为凹表面时,表面发射能量会被自身部分吸收；当表面k为凸表面时,发射能量不会被自身吸收.

对于Qg的理论表达式,一般情况下,若腔内气体充分混合,可假定等温[17],认为气体吸收系数a为常数.由气体透射率表达式τ(l)=exp(-al)和吸收率表达式α(l)=1-τ(l)=1-exp(-al),根据灰体发射率与吸收率相等,可得发射率ε(l)=1-exp(-al).气体发射而被表面k 接收的能量可以表示为

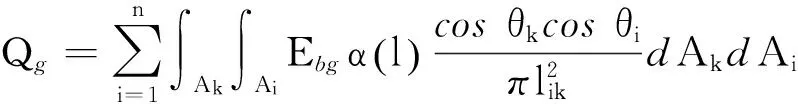
(2)

式中：各参数含义如图1所示，Ak为表面k的面积,Ai为表面i的面积,Ebg为高温烟气的黑体辐射能量,α(l)为烟气发射率,lik为两面积元连线长度,θi、θk分别为两面积元法线与lik的夹角.

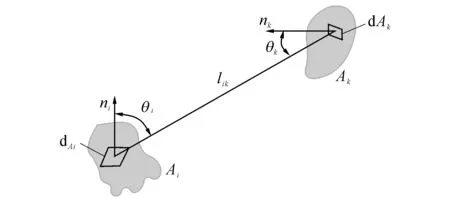
图1　传热分析示意图Fig.1　Schematic of heat transfer analysis

考虑角系数定义式[18-19]：

(3)

可将式(2)改写为

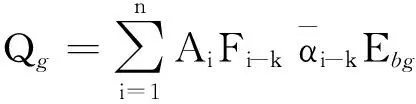
(4)

式中

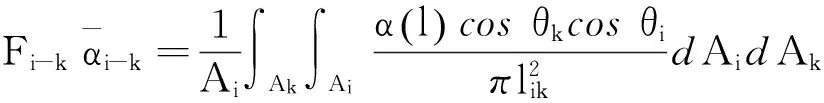
(5)

由此可将式(1)改写为

(6)

式(6)两端同时乘以表面k 的热势,则有

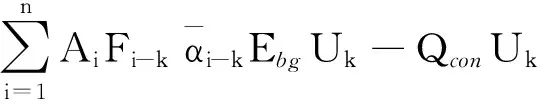
(7)

将Qk=εkAkUk代入式(7),可得

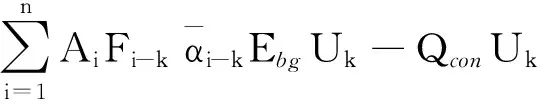
(8)

令

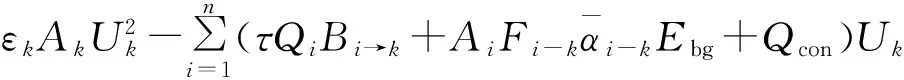
(9)

则有

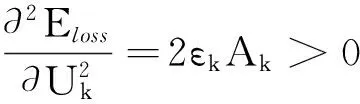
(10)

2算例与讨论

廉洁文化是社会主义先进文化的重要组成部分，是社会主义政治文明和精神文明的重要内容。在城乡社区开展廉洁文化建设，教育引导社区居（村）民提升思想政治素质、道德素质和法治意识，有利于营造风清气正的社区环境。

现代燃烧单元三维结构如图2所示,二维断面包括直线型、圆弧形、抛物线型三种结构,分别如图3(a)、(b)和图4所示,由燃烧筒外壁面1、锅底2、排气通道3、再辐射壁面4和连接圆弧5组成.图4中,固定抛物线上端点(A和A′ 点)和下端点(B和B′ 点),在燃烧筒轴线上任取一点C,即可得到不同结构抛物线型辐射阱,进而改变壁面间角系数分布,影响热效率等性能.现代燃烧单元工作时,高温火焰喷射进入燃烧筒并对其加热,烟气通过燃烧筒壁面开孔进入辐射阱,与燃烧筒壁面、再辐射壁面共同以辐射对流耦合方式将热量传递给受热体,并最终由排气通道流出.燃烧筒半径r =0.05m,连接圆弧段距燃烧筒高度h1=0.01m,排气通道高度h=0.02m.考虑现场实地条件,环境海拔1 905m,沸水温度T = 366K.假设锅底温度为沸水温度,烟气和燃烧筒壁面分别采用试验值1 500K和1 400K.

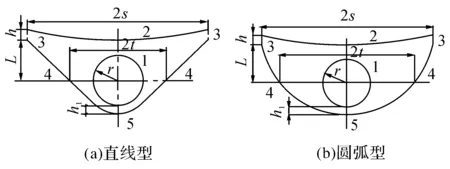
图3　辐射阱结构示意图Fig.3　Structural schematic of radiant well

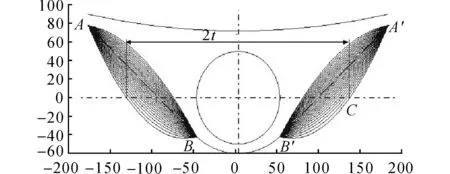
图4　抛物线型辐射阱结构示意图Fig.4　Structural schematic of parabolic radiant well

理论计算时,保持r、h和h1为定值,分析再辐射壁面开口宽度2t 、燃烧筒到烟气出口垂直距离L 和炉灶开口宽度2S 对现代燃烧单元热效率、传热量等性能的影响,计算过程采用Matlab编程实现.

3结果分析

3.1t对辐射阱热能利用的影响

由于结构关于轴线对称,现取其中一半进行分析.当L = 0.08m,S = 0.18m时,不同t下的辐射阱传热性能如图5所示.

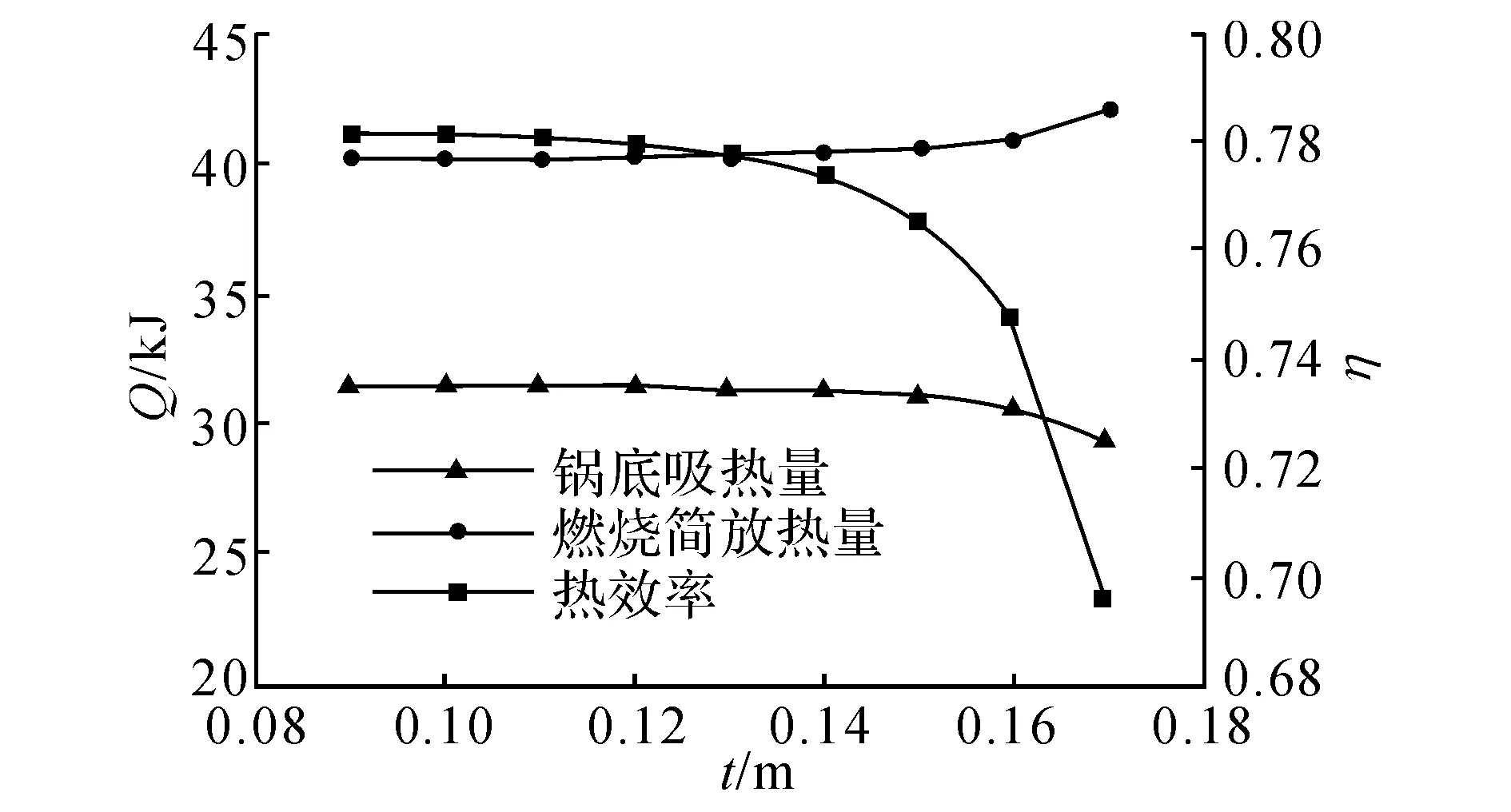
图5　不同t下的辐射阱传热性能Fig.5　Heat transfer performance of radiant well in different values of t

由图5可知,热效率和锅底吸热量均随 t 的增大而减小；C点越靠近燃烧筒,再辐射壁面所围空间越紧凑,当A′ 、B′ 、C三点共线,即再辐射壁面为直线型时,热效率最高；燃烧筒放热量随t 的增大而增大；t 越大,曲线变化越显著.

这是因为随 t 的增大,锅底有效辐射密度逐渐减小(此处以发射能量为正,吸收能量为负,下同).分析锅底净传热量可知,在其他结构参数不变的前提下,锅底吸热量随有效辐射密度的减小而减小；随 t 的增大,燃烧筒有效辐射密度逐渐减小.分析燃烧筒净传热量可知,在其他结构参数不变的前提下,燃烧筒放热量随有效辐射密度的减小而增大.

综上所述,随 t 的增大,锅底吸热量减小,燃烧筒放热量增大,因而热效率下降.该规律可由吸收系数分析求得：随 t 的增大,燃烧筒对锅底的吸收系数减小,导致可用能减少,热效率下降.

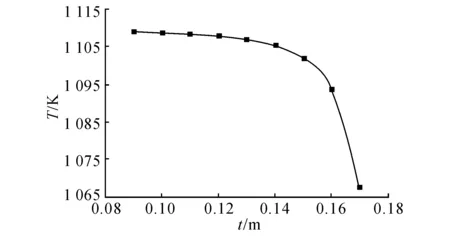
图6　不同t下的再辐射壁面温度Fig.6　Reradiation surface temperature in different values of t

3.2L对辐射阱热能利用的影响

当S=0.18m,t=0.09m时,不同L下的辐射阱传热性能如图7所示.

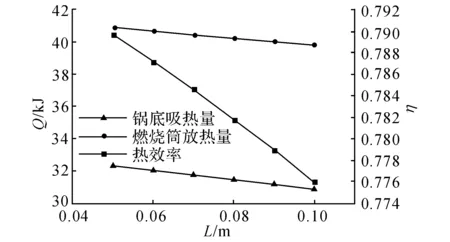
图7　不同L下的辐射阱传热性能Fig.7　Heat transfer performance of radiant well in different values of L

由图7可知,曲线均随L的增大而减小,且近似呈线性关系.这是因为随着L的增大,锅底有效辐射密度逐渐减小.分析锅底净传热量可知,锅底吸热量随有效辐射密度的减小而减小；随着L的增大,燃烧筒有效辐射密度逐渐增大.分析燃烧筒净传热量可知,燃烧筒放热量随有效辐射密度的增大而减小.

由图7还可以看出,锅底吸热量较燃烧筒放热量的变化更显著,因而热效率下降.该规律可由吸收系数分析求得：随L的增大,燃烧筒对锅底的吸收系数减小,导致可用能减少,热效率下降.

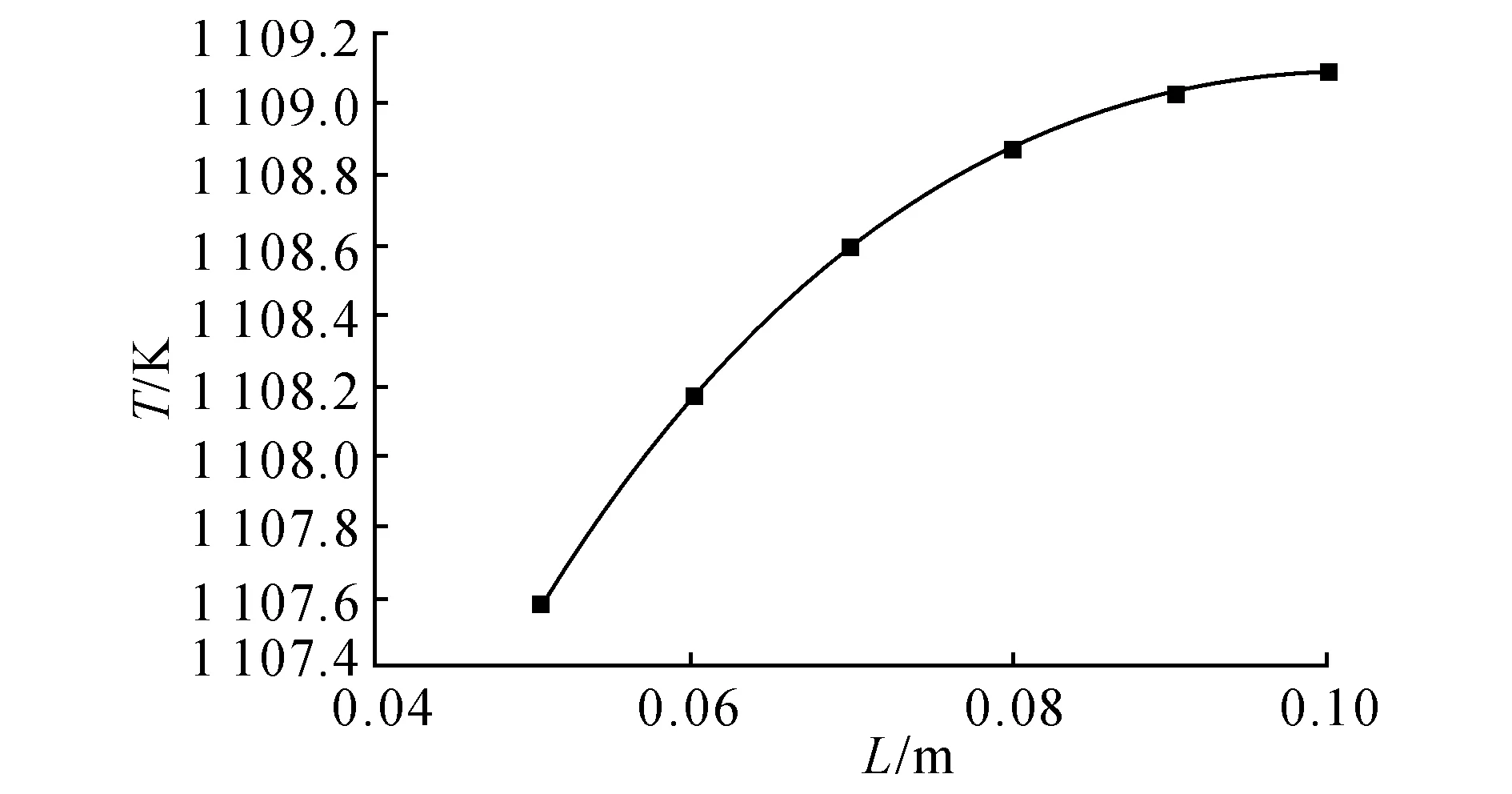
图8　不同L下的再辐射壁面温度Fig.8　Reradiation surface temperature in different values of L

3.3S对辐射阱热能利用的影响

由于结构关于轴线对称,现取其中一半进行分析.当L=0.08m,t=0.09m时,不同S下的辐射阱传热性能如图9所示.

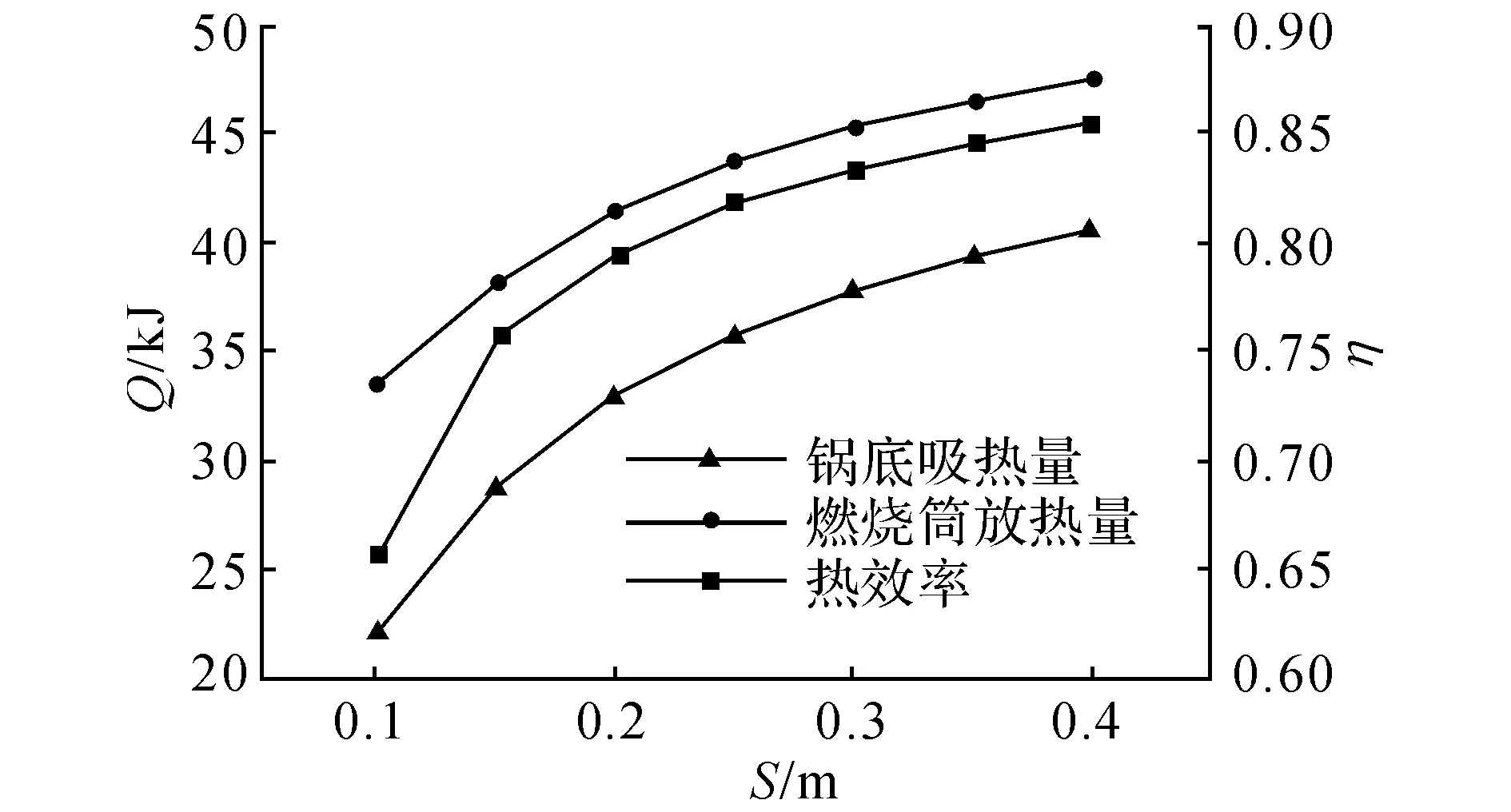
图9　不同S下的辐射阱传热性能Fig.9　Heat transfer performance of radiant well in different values of S

由图9可知,曲线随S的增大而增大；S越大,曲线变化越平缓.这是因为随S的增大,锅底有效辐射密度逐渐增大.分析锅底净传热量可知,锅底吸热量随有效辐射密度的增大而增大；随S的增大,燃烧筒有效辐射密度逐渐减小.分析燃烧筒净传热量可知,燃烧筒放热量随有效辐射密度的减小而增大.

由图9还可以看出,锅底吸热量较燃烧筒放热量的变化更显著,因而热效率上升.该规律可由吸收系数分析求得：随S的增大,燃烧筒对锅底的吸收系数增大,导致可用能增加,热效率上升.

对比图7、9可知,热效率随S的变化更显著,因此选取合理的S是结构优化和保证热效率的首要因素.

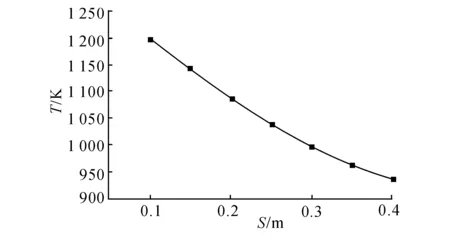
图10　不同S下的再辐射壁面温度Fig.10　Reradiation surface temperature in different values of S

4结论

(2)现代燃烧单元热效率随再辐射壁面开口宽度、燃烧筒到烟气出口垂直距离的增大而减小,随炉灶开口宽度的增大而增大；再辐射壁面温度随再辐射壁面开口宽度、炉灶开口宽度的增大而减小,随燃烧筒到烟气出口垂直距离的增大而增大.

(3)炉灶开口宽度为现代燃烧单元的关键结构参数,热效率随炉灶开口宽度的变化最显著.

参考文献(References)：

WANGSong-ping,CHENQing-lin,ZHANGBing-jian.Entransytransferequationanditsapplication[J].ScienceBulletin,2009,54(15)：2247-2251．

CHENGXue-tao,XUXiang-hua,LIANGXin-gang.Radiativeentransyfluxinenclosureswithnon-isothermalornon-grey,opaque,diffusesurfacesanditsapplication[J].ScienceChina,2011,41(10)：1359-1368．

CHENGXue-tao,LIANGXin-gang.Entransytheoryanditsapplicationintheprocessofheat-workconversion[J].ActaPhysicaSinica,2014,63(19)：190501．

[4]ONSAGERL.ReciprocalrelationinirreversibleprocessⅡ[J].PhysicalReview,1931,38:2265-2279．

[5]ONSAGERL,MACHLUPS.Fluctuationsandirreversibleprocesses[J].PhysicalReview,1953,91(6)：1505-1512．

[6]PRIGOGINEI.Introductiontothermodynamicsofirreversibleprocesses[M].3rded.NewYork：IntersciencePublisher,1967．

[7]冯长根.热学新理论及其应用[M].北京：中国科学技术出版社,2010．

CHENLin-gen.Entransytheoryanditsapplicatingprogress[J].ScienceBulletin,2012,57(30)：2815-2835．

[9]李志信,过增元.对流传热优化的场协同理论[M].北京：科学出版社,2010．

GUOJiang-feng,CHENGLin,XUMing-tian.Entransydissipationnumberanditsapplication[J].ScienceBulletin,2009,54(19)：2998-3002．

DINGKai-qiang,TIANMao-cheng,LENGXue-li.Optimizationforflowfieldofoutsidetubebasedonentransyextremeprinciple[J].JournalofEngineeringThermophysics,2015,36(2)：419-422．

GUOZeng-yuan,LIANGXin-gang,ZHUHong-ye.Entransy：aphysicalquantitydescribingheattransferability[J].ProgressinNaturalScience,2006,16(10)：1288-1296．

[13]GUOZeng-yuan,ZHUHong-ye,LIANGXin-gang.Entransy:aphysicalquantitydescribingheattransferability[J].InternationalJournalofHeatandMassTransfer,2007,50(13-14)：2545-2556．

[14]过增元,程新广,夏再忠.最小热量传递势容耗散原理及其在导热优化中的应用[J].科学通报,2003,48(1)：22-25．

GUOZeng-yuan,CHENGXin-guang,XIAZai-zhong.Leastdissipationprincipleofheattransportpotentialcapacityanditsapplicationinheatconductionoptimization[J].ScienceBulletin,2003,48(1)：22-25．

[15]程新广,李志信,过增元.基于最小热量传递势容耗散原理的导热优化[J].工程热物理学报,2003,24(1)：94-96．

CHENGXin-guang,LIZhi-xin,GUOZeng-yuan.Heatconductionoptimizationbasedonleastdissipationprincipleofheattransportpotentialcapacity[J].JournalofEngineeringThermophysics,2003,24(1)：94-96．

[16]CHENGXue-tao,LIANGXin-gang.Entransyfluxofthermalradiationanditsapplicationtoenclosureswithopaquesurfaces[J].HeatMassTransfer,2011,54:269-278．

[17]卞伯绘.辐射换热的分析与计算[M].北京：清华大学出版社,1988．

[18]SIEGELR,HOWELLJR.Thermalradiationheattransfer[M].2nded.WashingtonDC:HemisphereandMcGraw-Hill,1981．

[19]INCROPERAFR,DEWITTDP,BERGMANTL,etal.Fundamentalsofheatandmasstransfer[M].6thed.NewYork:Wiley,2007．

收稿日期：2015-04-10.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：中国石油大学(华东)研究生创新工程资助项目(YCX2015034).

作者简介：夏宇(1989-)，男，硕士生，从事炉灶节能优化研究．ORCID：0000-0002-6603-679X．E-mail：dkpylxy@163.com 通信联系人：仇性启，男，教授，博导．ORCID：0000-0002-5763-1968．E-mail：apvshi@upc.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.07.020

中图分类号：TK 11

文献标志码：A

文章编号：1008-973X(2016)07-1367-06

Heattransferinopeningsystemwithparticipatingmediums

XIAYu,QIUXing-qi,HUIYuan-yuan

(College of Chemical Engineering, China University of Petroleum, Qingdao 266580, China)

Abstract:The entransy balance equation on isothermal diffused gray body opening system with participating mediums was obtained based on the extremum entransy dissipation principle (EEDP) and coupled heat transfer of radiation and convection between high temperature gas and solid surface. The validity of the equation was proved and the application field of entransy theory was expanded. For the structural analysis of modern burning unit, some parameters’ (reradiation surface opening width, vertical distance between burning tube and gas outlet and stove opening width) influencing laws on thermal efficiency, heat transfer quantity of pan and burning tube and reradiation surface temperature were obtained by theoretical calculation with application of the equation through the software Matlab. The stove opening width was the key structural parameter of affecting heat transfer performance of modern burning unit．

Key words:entransy dissipation；isothermal diffusion；heat transfer；modern burning unit