通过层次分析法分析大学生毕业后去向问题
2016-08-04杨之光
杨之光
(东北财经大学 管理科学与工程学院,辽宁 大连 116023)
通过层次分析法分析大学生毕业后去向问题
杨之光
(东北财经大学 管理科学与工程学院,辽宁 大连 116023)
层次分析法(AHP)是运筹学下的一个分支方法,是一种将与决策相关的各个因素逐一分解成目标、准则、方案等各个层次,并在此基础之上进行定性定量分析的一种方法。这种方法主要对解决一些定性问题有参考价值。本文从大学生角度出发,首先列举出大学生面临的毕业选择及其利弊,通过假设一名学生对各项影响因素看法的权重,再通过层次分析法得出各种选择的权重对比来辅助大学生进行选择,有重要参考意义。
层次分析法;大学生;毕业;判断性指标
1 我国大学本科毕业生就业现状
随着我国大学本科毕业生人数的急剧增长和本科教育整体水平的下降,使就业问题成为了一个日益困扰着我国大学生的重要问题,而伴随着社会的进一步发展,如今大学生的毕业选择也比以前有所增加,比如:出国继续深造或创业。那么对于现在大学生来说,如何选择一条适合自己的道路成为了摆在面前的关键问题。
2 基本假设
笔者假设,在以下的模型是从以一个大学生的主观角度来进行分析设定的。在本例中所有各列的准则因素均符合层次分析法的基本要求,模型分析各个因素较为全面,各项因素的权重是从一名大学生的角度而设计的。而且笔者假定一个人选择了读研或是出国,那在他完成学业之后还是会选择就业和创业两种方式。但是由于他在就业或创业的时间上始终比同龄人有所欠缺,在部分因素上存在劣势。
3 问题分析
在对当下大学生的选择有了初步了解,并进行概括之后,可以假设有4项选择:考研、出国、就业和创业。运用层次分析法将各项因素进行量化对比分析,用两个模型分别陈述其优劣来说明这一点,最后用权重之比来判断那个选择是对于这位大学生来讲是最好的。层次分析结构模型分为3个部分,分别是目标层、准则层和方案层。模型一般都由三层组成,有些模型的准则因素过多导致了决策层会被分为不止一层。处在同一层的元素彼此对上层元素有影响,同时又对下层元素起到了支配的作用。笔者从最顶层出发,通过两两比较,用描述判断矩阵的方法来描述这一名大学生对不同选择差异的权重,通过对问题较为准确的分析,得出元素相互两两比较的次序。通过合理的设定和权重的分析,各个矩阵间往往都是符合一致性假设的。最后通过计算得出4项选择之间优劣两项的权重情况,再通过对每种选择的优劣之比确定出对这位大学生最合理的选择方案。
4 建立层次分析模型比较权重
在大学毕业出路的选择上,可以大致分为考研、出国、工作和就业4个方向,只需设定这4种目标即可。在Yaahp软件中首先画出这4项备选方案。接下来进一步分析,将4条道路的益处分为能力提升、经济利益的增加和知识水平提高3个部分。再一次细分为8个有利因素如图1所示。
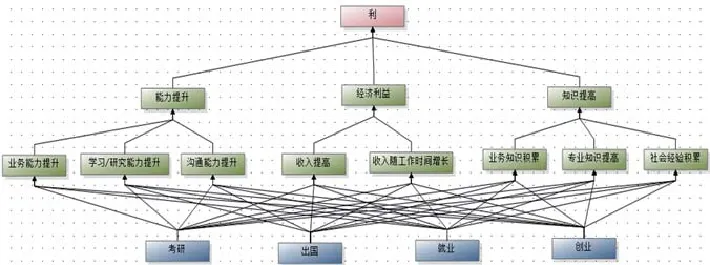
图1 大学生各项选择与各自优势关系图
笔者分别用1、3、5、7、9来表示不同的重要性特征,1表示比较的双方同等重要,3表示较重要,5表示重要,7表示很重要,9表示绝对重要。2、4、6、8分别表示位于每两个标度的中间值。
将各种选择可能产生的优势大致归结为3类,分别是能力提升、经济效益、知识提高,然后分析出成对对比矩阵,见表1。
另一方面,大学生无论作出哪样的选择,相比其他选择不仅会有优势,也会有劣势。通过对这些弊端进行了一系列的分析,最终确认了主要的4个方面的问题。
将各种选择可能产生的各项弊端大致归结为4类,分别是专业知识的缺乏、时间流失、成本增加和事业的风险,然后分析出成对对比矩阵。
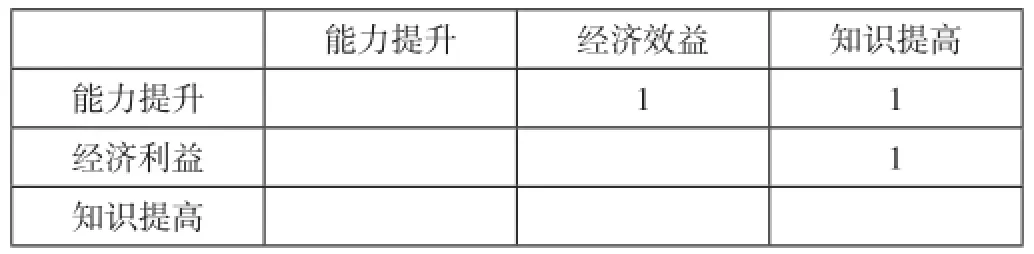
表1 决策目标“利”(A1)的重要性比较(其他权重对比暂略)
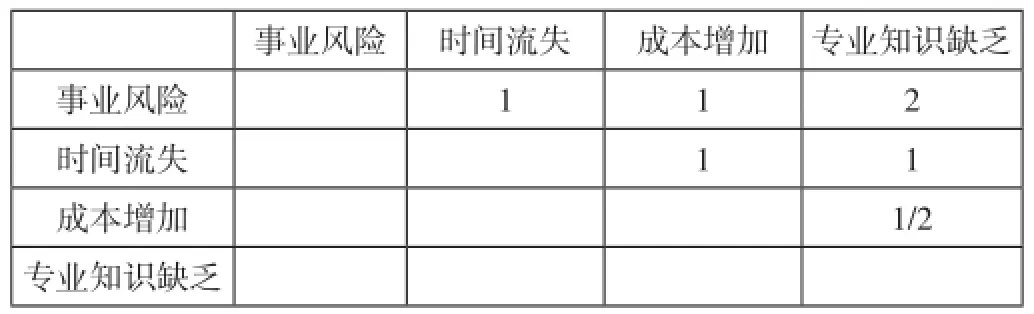
表2 决策目标“弊”(A1)的重要性比较
决策目标“专业知识缺乏”(B1)的重要性比较,决策目标“时间流失”(B2)的重要性比较和决策目标“成本增加”(B3)的重要性比较图省略。
选择创业、就业、出国、考研所面临的事业风险的大小,见表3。
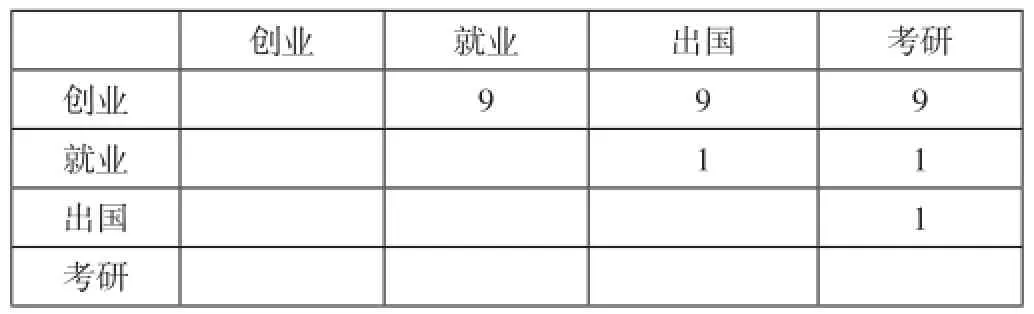
表3 决策目标“事业风险”(B4)的重要性比较
在此之后对上述各项的两两判断矩阵进行一致性检验,一致性检验往往由3部分构成:①计算一致性指标CI;②查找相应的一致性随机性指标RI;③计算一致性比例CR。在得出这些关系之后,可以使用MATLAB和Yaahp等软件进行运算。
5 结果与分析
通过对Yaahp层次分析法软件的使用,可以得出每一项的特征值和最终方案的权重比较情况,结果由表4所示。显而易见,可以得出结论,就这名大学生的个人偏好来说,选择大学毕业之后继续出国深造是一个最优的选择。
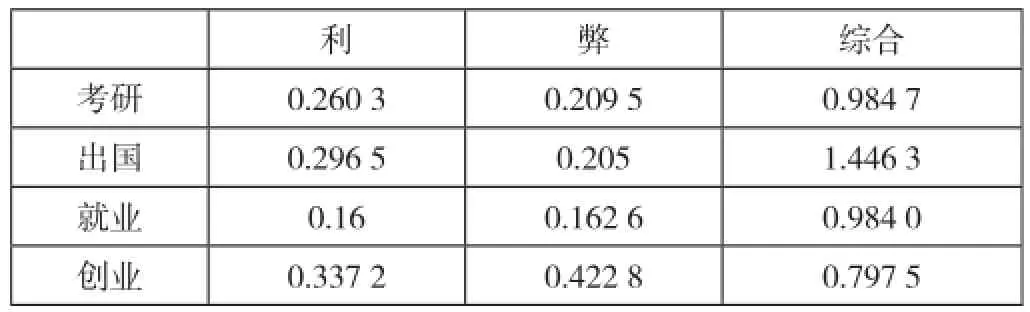
表4 四种选择结果对比
6 模型推广及评价
(1)本文从一个大学生的角度出发,对其选择角度进行分析,充分考虑概括了他所面临各种选择的利弊,具有推广性。
(2)本文使用了层次分析的方法,通过对一个定性问题引入定量模型, 从正反两个方面分别进行分析,比单一框图显得更加丰富,结果的可信度也大大提高。
(3)本文的实用性比较强,也可以按照每个人不同情况来调整权重从而得出不同的结果,因人而异。
主要参考文献
[1]王莲芬,许树柏.层次分析法引论[M].北京:中国人民大学出版社,1990.
[2]高瑞.大学生毕业去向选择的数学模型[J].中国科技信息,2010(19).
10.3969/j.issn.1673 - 0194.2016.10.159
G647.38
A
1673-0194(2016)10-0230-02
2016-04-08
