考虑构件重要性的导管架平台强度储备提升

吴庆金, 杨飏

(大连理工大学 船舶工程学院，辽宁 大连 116024)



考虑构件重要性的导管架平台强度储备提升

吴庆金, 杨飏

(大连理工大学 船舶工程学院，辽宁 大连 116024)

摘要：导管架平台空间造型复杂，杆件和节点数量繁多，局部冗余度虽然高但总体分布不均匀。同时，平台质量大多集中于上部结构，局部构件的破坏可能导致结构在重力载荷作用下发生连续性倒塌。本文在导管架平台常遇的冰工况载荷作用下，对移除各个构件后的缺陷结构进行推覆分析，得到各构件重要性指标，依此判断每个构件的重要性；分析不同首失效构件导致的结构薄弱路径，从而确定结构的最薄弱路径和路径起始构件位置；进而，在保证总用钢量不变的条件下，调整构件截面设计，实现结构薄弱环节的调控。研究表明：通过构件重要性分析的方法，可以较有效地确定结构薄弱路径；通过调整薄弱路径首个构件的方法，可以实现薄弱路径的调整，结构的极限承载力提高10%以上，极限变形降低10%左右。

关键词：导管架平台；推覆分析；构件重要性指标；塑性发展路径；薄弱环节

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160127.1137.024.html

导管架式海洋平台是近海油气资源开发的主要工程结构物，其所处海洋环境非常恶劣，除正常的工作载荷和环境载荷作用，还时常遭受船舶碰撞、爆炸和火灾等事故的威胁，局部构件破坏的情况时有发生。当导管架平台局部杆件破坏时，会导致结构极限承载力降低，并有可能导致结构整体失效，造成大量的人员伤亡和经济损失，为了降低海洋平台结构整体倒塌事故发生的可能性，要求海洋平台结构应具有较高的强度储备[1]。目前针对导管架平台结构强度储备的研究主要通过静力推覆[2]或增量动力分析[3]实现。导管架平台是高冗余度结构，各构件在结构中的重要性程度有差异，对导管架平台结构进行构件重要性分析，可以明确结构体系中不同构件的作用，反映结构中局部杆件失效对结构极限承载力和失效路径的影响，加深设计者对结构体系的认识，并指导考虑鲁棒性的结构设计[4]。

对于导管架海洋平台结构构件，一般定性的认为导管腿和桩为1类构件，与导管腿或桩连接的水平横撑为2类构件，竖向斜撑为3类构件。定性的分类方法不能明确各类构件对结构的影响程度，需要对构件重要性进行定量分析，并深入探讨各构件在结构中的作用。目前，对结构进行构件重要性评价的方法主要为对比移除构件前后结构性能指标的变化，而结构的性能指标有结构刚度、强度、冗余度、变形能和可靠性等。Pandy等[5]将移除构件后结构响应变化定义为敏感性，敏感性指标高的构件是结构中的重要构件。Nafda[6]以移除构件前后结构刚度矩阵行列式比值作为构件重要性指标；Gharaibeh等[7]将构件重要性指标定义为该构件对结构整体可靠性的影响。目前对结构加强一般通过层间位移角判断薄弱层，对薄弱层梁柱进行加强实现对失效路径的控制[8]，而通过构件重要性分析，可以对局部重要构件进行调整，实现有针对性的加强设计。

本文将建筑结构中常用的构件重要性分析方法应用于导管架平台结构，在分析过程中记录结构的响应信息和杆件塑性状态信息，并分析移除构件对整体结构和剩余杆件的影响。在构件重要性指标的基础上对导管架平台结构进行加强设计，结构的塑性发展路径得到有效调整，结构极限承载能力得到较好提升。

1构件重要性分析的基本理论

1.1构件重要性评价方法

构件重要性系数是衡量构件重要性程度的指标，它不仅取决于结构系统本身的力学性能，也取决于作用载荷情况，还与结构性能的评价指标相关[9]。表1中总结了当前构件重要性指标的主要分析方法及其含义，并对各类指标的优缺点进行评价。

表1　构件重要性指标

注：K为完好结构刚度指标,Ki为移除i构件结构刚度指标,SRj为构件最大应力比,U为完好结构变形能,Ui为移除第i根构件结构的变形能,λo为完好结构极限承载力,λi为移除i构件结构极限承载力,βo为完好结构可靠性指标,βi为移除i构件的可靠性指标,ki为各分项影响权重,Yi为分项因素。

1.2构件重要性评价指标的选择

综合分析各类构件重要性指标，基于刚度的构件重要性指标未考虑载荷作用，基于强度和变形能的指标无法确定结构极限承载下的性能，基于可靠性的指标需要对诸多因素进行假定，缺乏统一的说服力，基于结构承载力的构件重要性指标虽然计算量大，但是可以考虑材料非线性的影响并且可以反映结构的极限承载能力，本文以承载力指标作为构件重要性指标。

目前常以结构损伤前后承载力变化作为结构冗余度的测度，则构件失效对结构冗余度的敏感性即构件重要性系数，Curley等[10]给出结构冗余度参数的计算公式：

(1)

式中：R表示结构冗余度指标，λ0为完好结构极限承载力，λ*为结构构件受损后的结构极限承载力。

完好结构和损伤结构极限承载力可以通过强度储备比(RSR)和剩余强度比(DSR)直观的表现，其中RSR指标和DSR指标的计算公式为

(2)

(3)

式中λd为结构设计承载力。引入RSR和DSR指标后，极限承载力指标的构件重要性系数可以表示为

(4)

2导管架平台构件重要性分析

2.1结构模型建立

针对图1所示的导管架平台结构进行构件重要性分析。导管架平台为四腿桩基式结构，结构水平两方向对称，斜撑对角型布置。导管架桩腿截面直径1.2 m，壁厚0.05 m；横撑构件截面直径0.78 m，壁厚0.038 m；斜撑构件截面直径0.51 m，壁厚0.025 4 m。平台设计水深33.8 m，平台总重量为1 465×103kg，其中上部甲板重量为784×103kg，支撑结构总重量为682×103kg。对结构进行平面展开并对杆件予以编号如图2所示。

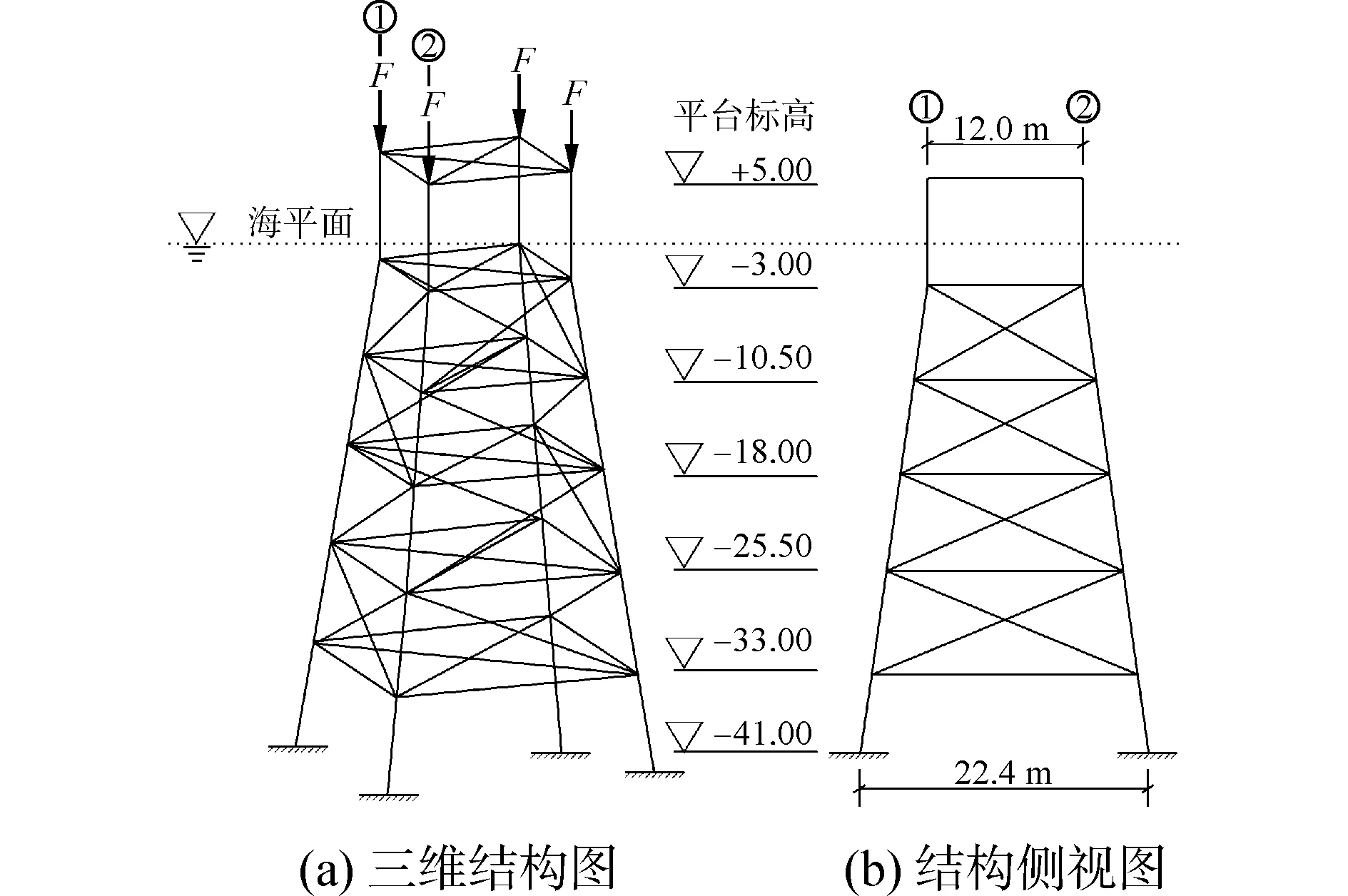
图1　平台结构模型Fig.1　Model of platform structure

采用ANSYS软件建立有限元模型。由于主要研究对象是下部导管架结构，建模时将上部甲板结构略去，上部甲板结构以如图1中4个集中力F的形式施加在导管架端帽处的节点上。对泥面以上的构件采用PIPE288单元模拟，可以考虑海流作用；泥面以下的桩腿采用BEAM188单元模拟，可以考虑结构剪切变形的影响。平台桩土相互作用简化为等效桩方法，将导管架平台约束条件模拟为刚性固定端，刚性固定端位于设计泥面垂直以下6倍桩直径处。平台选用Q235钢材，材料屈服强度为235 MPa，杨氏模量为210 GPa，泊松比为0.3，密度为7 850 kg/m3。

图2　平台侧面展开图及杆件编号Fig.2　Flank figure of platform and number of members

2.2载荷工况选取

为了得到导管架平台结构的强度储备指标，本文对结构进行推覆分析。对结构进行推覆分析的结果在很大程度上与所选择的侧向载荷分布模式相关，常见的分布形式有：顶点集中力形式、均匀分布形式、基本振型分布形式和多振型分布形式等。考虑到导管架平台结构安全影响主要来自于外部环境且水面处环境载荷较大的特点，本文选取载荷类型为冰工况，冰厚、风速和水面流速均采用极值Ⅰ型分布，各类载荷的分布参数[1]如表2所示，不同重现期下的冰厚、风速和水面流速可以通过下式求得：

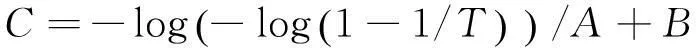
(5)

式中：A和B为各类载荷极值Ⅰ型分布的分布参数，T为重现期，C为冰厚、风速或者水面流速。

在浅海区，流速随水深的变化规律可以表示为

(6)

式中：us为水面流速,d为水深,z为自海底以上高度。

表2　环境载荷要素分布

根据式(5)得到不同重现期下的风速、冰厚和水面流速。然后，根据浅海固定平台规范[11]中给出的计算方法得到相应的风载荷、冰载荷和不同水深条件下的海流载荷。将风载荷以水平作用集中力的形式施加于导管架端帽处的四个节点；在考虑遮蔽效应的前提下，将冰载荷以水平作用力的形式施加于水面处的结构节点；将海流载荷以水平分布力的方式施加于水面以下结构构件上。

导管架海洋平台所受载荷方向随机性比较大，为降低载荷方向对构件重要性指标的影响，考虑载荷方向如图3所示。由于结构水平两方向对称，对称构件的重要性程度一致，只需对图3中ab面和cd面内构件进行移除分析，当移除ab面内外围横撑、斜撑和主导管构件时，考虑载荷方向为0°、45°、90°、135°和180°；当移除cd面内横撑构件时，考虑载荷方向为45°、90°、135°、180°和225°。

图3　载荷作用方向Fig.3　The direction of loading

2.3构件重要性分析流程

4) 4台推进器变压器，容量为5 300 kVA/2 650 kVA/2 650 kVA,电压变比11 kV/0.71 kV/0.71 kV。

基于推覆分析得到结构极限承载力的构件重要性分析流程如图4所示，分析步骤为：

1)计算50年一遇载荷工况，对导管架平台结构进行分析，并以该工况作用下的结构基底剪力作为结构设计承载力。

图4　构件重要性分析流程Fig.4　Flow diagram of component importance analysis

2)以重现期逐渐增长的方式增加载荷并对导管架平台结构进行分析，记录每一载荷工况下的基底剪力与顶点位移信息。

3)逐渐增加载荷直到计算程序不收敛时刚度矩阵奇异，则认为结构达到极限承载状态。

4)得到完好结构在45°和90°方向的RSR指标和移除构件后结构在图3载荷工况下的DSR指标，以各方向下求得的构件重要性系数最大值作为该移除构件的重要性指标。

2.4导管架平台构件重要性指标

完好结构在45°和90°载荷方向下设计基底剪力为7.92×103kN和4.76×103kN, 结构在45°和90°方向极限状态对应的基底剪力为2.08×104kN 和1.76×104kN，则完好结构在45°和90°方向的RSR指标分别为2.622和3.690。根据API RP 2A规范，合理设计的导管架平台储备强度系数约在1.8～2.4，可以看出，该导管架海洋平台结构设计储备强度较高。

表3　构件重要性指标

3移除构件影响分析

为研究不同类型构件对剩余结构的影响，分别取移除3号腿柱、移除36号外围横撑、移除57号内部横撑和移除73号斜撑结构与完好结构进行对比分析。在90°方向冰工况载荷作用下，完好结构和移除构件后剩余结构的基底剪力与顶点位移如图5所示。横撑构件的重要性指标较小，对应的基底剪力与顶点位移基本没有变化。完好结构弹性阶段斜率为1.10×105kN/m，移除73号斜撑后结构弹性阶段的斜率为8.2×104kN/m，结构刚度降低25.5%；移除3号腿柱后剩余结构弹性阶段的斜率为6.3×104kN/m，结构刚度降低42.7%。

进一步分析移除73号斜撑构件后结构传力路径的改变情况。在移除73号斜撑结构达到极限状态载荷条件下，对比完好结构与移除构件后剩余结构的应变能变化如图6所示。将移除73号斜撑后变形能变化比较大的杆件用粗线表示在结构侧面展开图中，如图7所示。从图中可以看出73号斜撑构件移除导致应力重分布到相邻层与载荷平行立片的横撑和斜撑构件上。

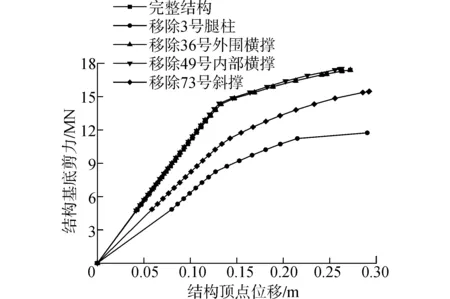
图5　结构基底剪力与顶点位移关系曲线Fig.5　Base shear-roof displacement curves of structure

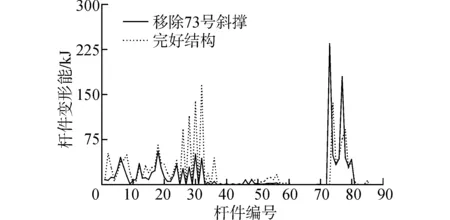
图6　构件变形能Fig.6　Strain energy of members

图7　传力路径变化Fig.7　Change of force transfer path

4基于构件重要性的结构塑性发展路径调整

通过对海洋平台结构进行推覆分析，可以得到在相应载荷工况下的塑性发展路径，而结构的极限承载力是由塑性发展路径上构件的承载能力决定的。构件重要性指标可以反映各构件对结构承载性能的敏感性，在构件重要性的基础上可以对结构进行针对性的加强设计。

4.1结构塑性发展路径

记录各杆件截面的塑性状态，在杆件截面上取32个栅点并记录其应变状态。当栅点处出现塑性应变时，认为杆件在该处进入塑性，栅点位置如图8所示。

导管架平台在90°方向冰工况载荷推覆分析时的塑性发展路径如图9所示，可以看出，当基底剪力达到12×103kN时73和77号斜撑构件出现塑性，其后，最底部的桩腿构件进入塑性，当基底剪力达到18×103kN时，26、28、30、32、54、56、74和76号杆件也出现塑性。而结构的塑性发展路径代表结构的薄弱环节。

图8　杆件截面Fig.8　Cross section of member

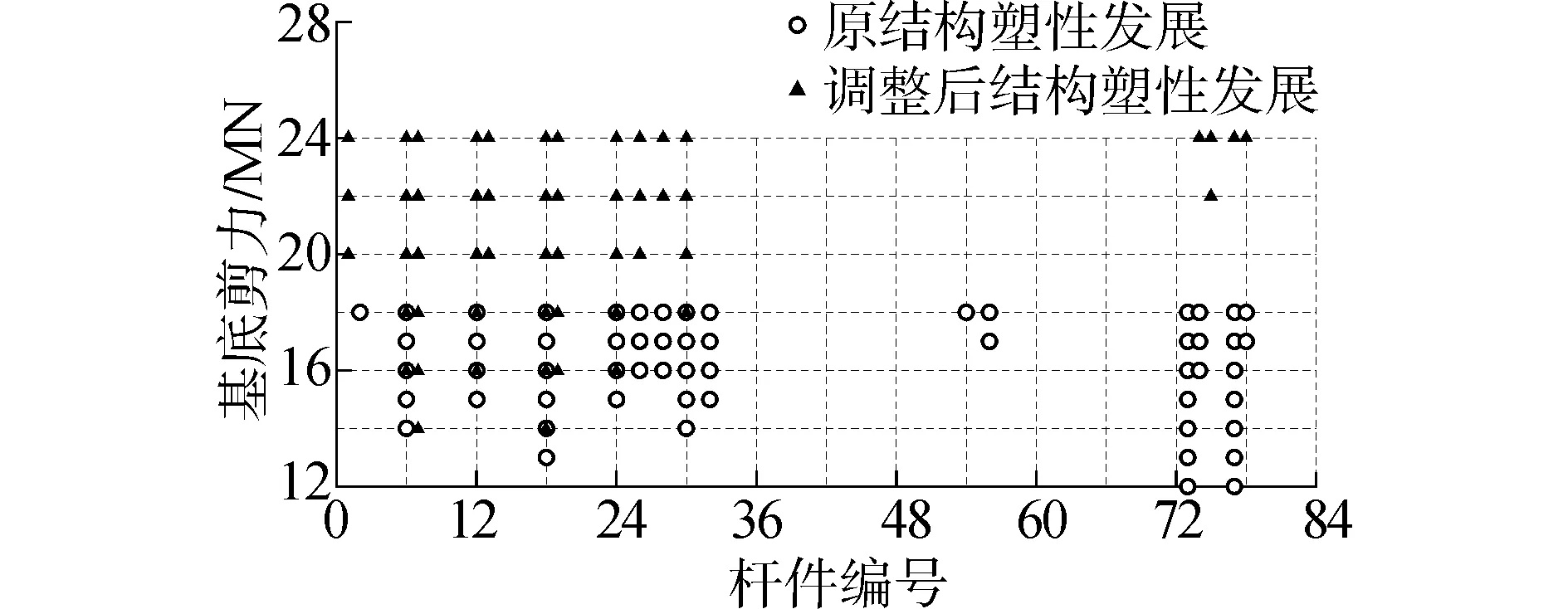
图9　结构塑性发展过程Fig.9　Plastic development of structure

4.2构件截面调整

73号斜撑构件所在层的斜撑重要性程度较高，且该层斜撑在冰工况下首先进入塑性，因此选择该层斜撑构件截面进行调整。在导管架结构总用钢量不变的前提下对73号斜撑构件所在层的所有斜撑构件进行加强，将原始壁厚由2.54 cm增加为2.7 cm，对重要性程度不高的第一层外围横撑构件进行削弱，壁厚由原来的3.8 cm降低为3.74 cm。

对调整后结构进行冰工况下的推覆分析，载荷方向分别为45°和90°。90°方向下的塑性发展过程如图9所示。从结果可以看出，结构中首个进入塑性的构件位置发生变化，当基底剪力达到14×103kN时，6号和18号腿柱开始进入塑性；当基底剪力达到16×103kN时12和24号腿柱开始进入塑性；其后，26号和30号外围横撑出现塑性；当基底剪力达到24×103kN时，74、77和78号斜撑构件出现塑性。为进一步分析结构构件进入塑性程度，以栅点处不同程度进入塑性杆件占总杆件数的比值作为杆件塑性率，原结构与调整后结构杆件塑性率如图10所示。可以看出，对于调整后结构，在极限状态下1/4截面进入塑性的杆件率增大2.3%，全截面进入塑性的杆件率降低2.3%。调整后能更好地发挥构件的承载能力，而全截面进入塑性的杆件比率降低可保证结构具备更好的极限储备。

调整后结构在45°和90°方向的RSR指标分别为2.949和4.731，分别比原结构提高12.5%和28.2%。调整结构相比原结构在45°和90°方向极限变形分别降低8.1%和15.5%，调整后结构基底剪力与顶点位移曲线如图11所示，原结构在45°和90°方向弹性阶段的斜率为1.10×105kN/m，调整后结构在45°和90°方向弹性阶段的斜率为1.43×105kN/m，调整后结构整体刚度提高30.0%左右。在原结构达到极限状态载荷条件下，对比调整后结构的层间位移，73号斜撑所在层的层间位移明显降低，90°方向结构顶点位移降为原来的一半左右，45°方向结构顶点位移降低19.9%，如图12所示。

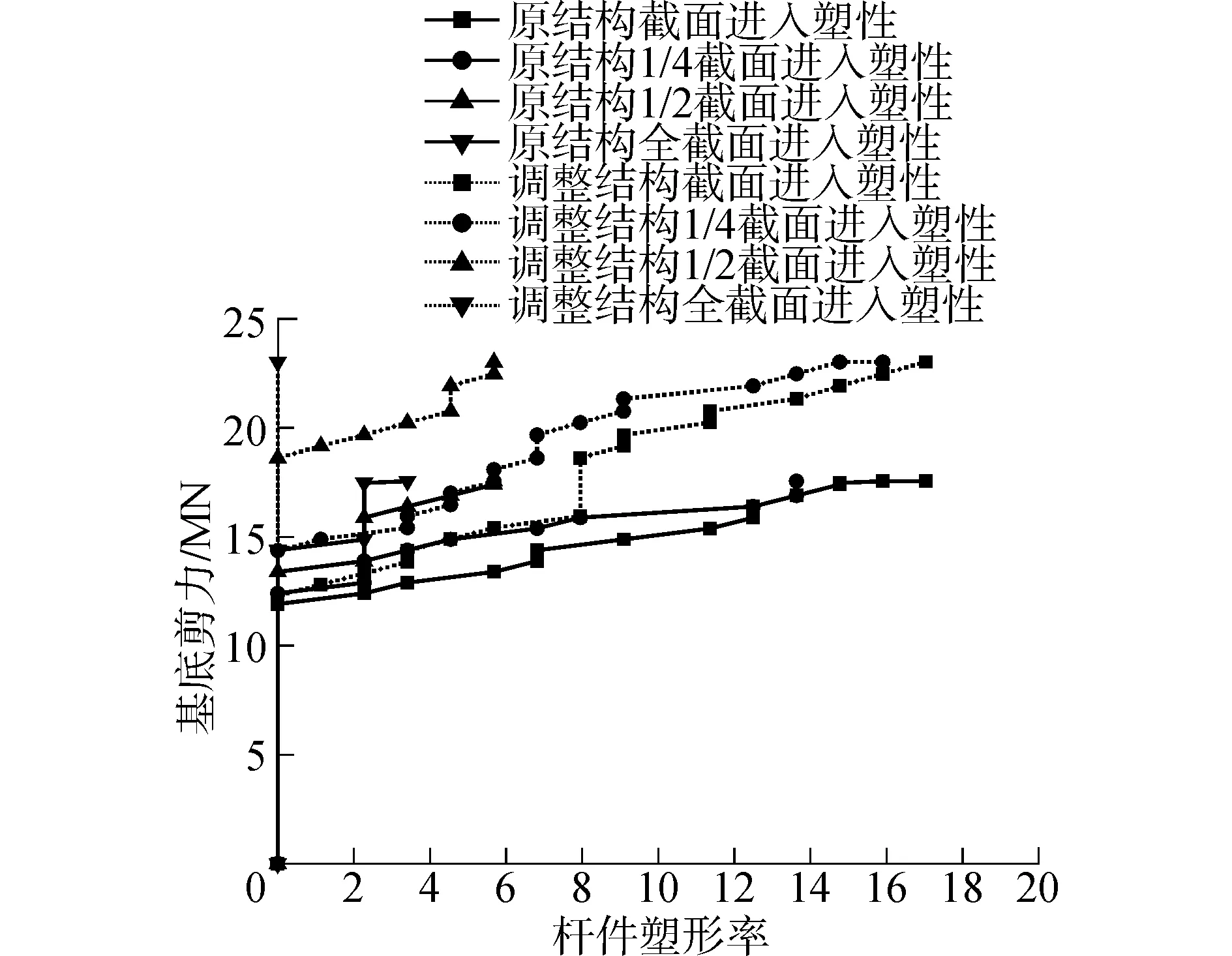
图10　杆件塑性率Fig.10　 plasticity ratio of member

图11　调整后结构基底剪力与顶点位移Fig.11　Base shear-roof displacement curves of adjusted structure

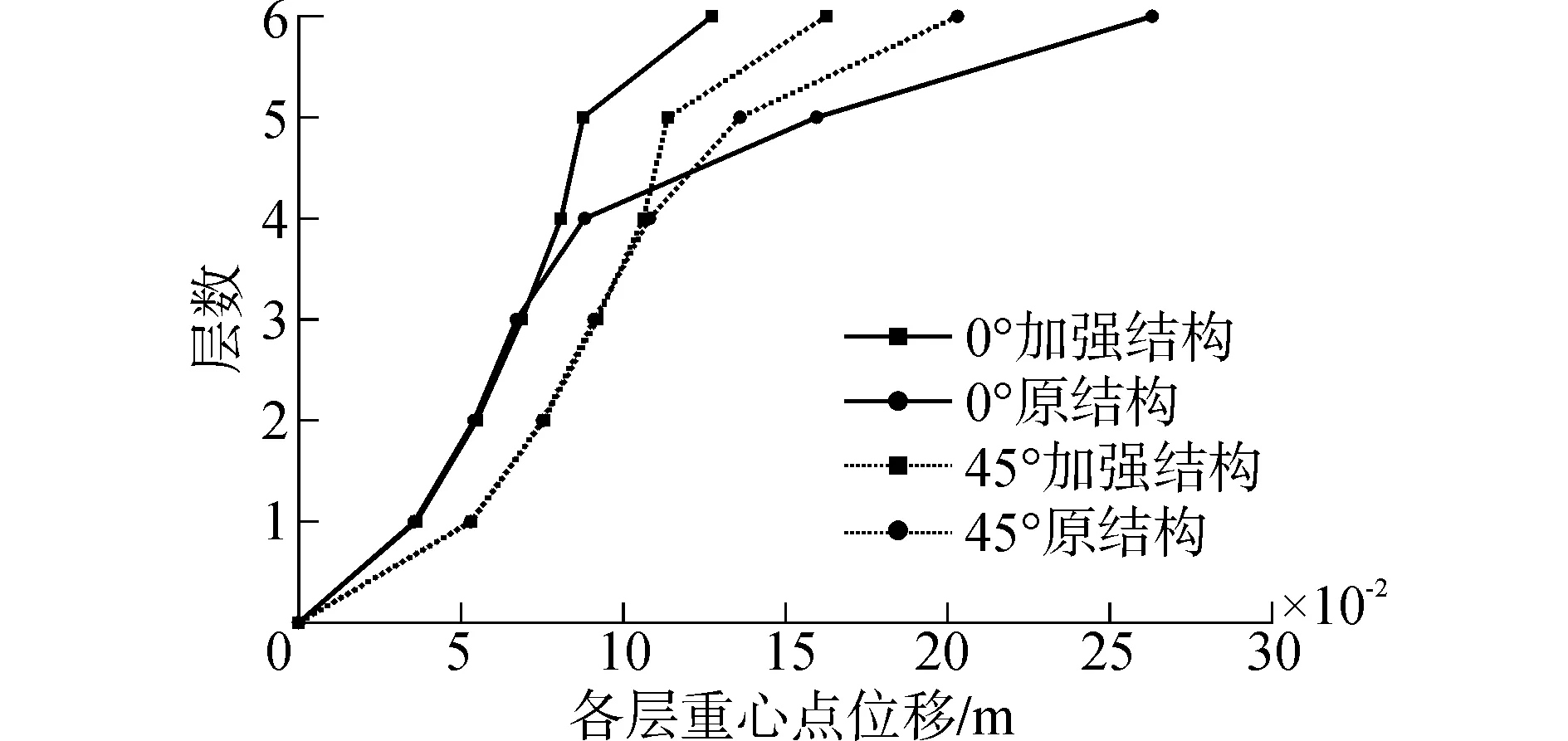
图12　结构层间位移Fig.12　Inter-story displacement

5结论

1)对于导管架平台结构，可以以移除构件前后结构冗余度的变化率作为构件重要性指标，而结构冗余度可以通过静力非线性推覆分析的方法实现，且应考虑载荷方向的影响。

2)以移除构件前后结构冗余度的变化率作为构件重要性指标，可以反映构件对结构极限承载能力的影响，依此可以判断每个构件的重要性程度并反映结构的薄弱环节；通过对比移除构件前后剩余构件变形能的变化可以反映移除构件对剩余杆件的影响。

3)在构件重要性分析的基础上，人为调整结构的塑性发展路径首杆件，可以有针对性的实现薄弱路径的调整，从而提高结构的极限承载能力，减小极限变形，充分发挥构件的承载能力。

参考文献：

[1]徐彻, 杨飏. 海上固定式平台结构安全储备研究综述[J]. 海洋工程, 2014, 32(1): 117-124.

XU Che, YANG Yang. Safety reserve of fixed offshore platform structures: a review[J]. The ocean engineering, 2014, 32(1): 117-124.

[2]BAI Yong, KIM Y, YAN Huibin, et al. Reassessment of the jacket structure due to uniform corrosion damage[J]. Ships and offshore structures, 2016, 11(1): 105-112.

[3]ASGARIAN B, RAZIEI A. Comparison of incremental dynamic and pushover analysis of jacket type offshore platforms[C]//ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering， 2007: 575-582.

[4]蔡建国, 王蜂岚, 冯健, 等. 连续倒塌分析中结构重要构件的研究现状[J]. 工业建筑, 2011, 41(10): 85-89.

CAI Jianguo, WANG Fenglan, FENG Jian, et al. Review of the key element for progressive collapse of structures[J]. Industrial construction, 2011, 41(10): 85-89.

[5]PANDEY P C, BARAI S V. Structural sensitivity as a measure of redundancy[J]. Journal of structural engineering, 1997, 123(3): 360-364.

[6]NAFDAY A M. System safety performance metrics for skeletal structures[J]. Journal of structural engineering, 2008, 134(3): 499-504.

[7]GHARAIBEH E S, MCCARTNEY J S, FRANGOPOL D M. Reliability-based importance assessment of structural members[J]. Computational fluid and solid mechanics, 2001, 1: 198-200.

[8]孙爱伏, 欧进萍, 侯爽. 高层钢框架结构的薄弱层加强与最弱失效模式控制[J]. 地震工程与工程振动, 2011, 30(6): 49-55.

SUN Aifu, OU Jinping, HOU Shuang. Weak story strengthening and weakest failure mode control of tall steel frame buildings[J]. Journal of earthquake engineering and engineering vibration, 2011, 30(6): 49-55.

[9]叶列平, 林旭川, 曲哲, 等. 基于广义结构刚度的构件重要性评价方法[J]. 建筑科学与工程学报, 2010, 27(1): 1-6, 20.

YE Lieping, LIN Xuchuan, QU Zhe, et al. Evaluating method of element importance of structural system based on generalized structural stiffness[J]. Journal of architecture and civil engineering, 2010, 27(1): 1-6, 20.

[10]FRANGOPOL D M, CURLEY J P. Effects of damage and redundancy on structural reliability[J]. Journal of structural engineering, 1987, 113(7): 1533-1549.

收稿日期：2014-11-28.

基金项目：国家自然科学基金项目(50908036)；辽宁省自然科学基金项目(201202040).

作者简介：吴庆金(1990-) 男，硕士研究生； 通信作者：杨飏, E-mail: yyang@dlut.edu.cn.

doi:10.11990/jheu.201411083

中图分类号：P751

文献标志码：A

文章编号：1006-7043(2016)04-0514-06

Improving strength reserve of a jacket platform considering component importance

WU Qingjin, YANG Yang

(Department of Naval Architecture, Dalian University of Technology, Dalian 116024, China)

Abstract：Space configuration of a jacket offshore platform is complex with numerous of members and joints. The partial redundancy of structure is high, but the overall distribution is uneven. Meanwhile, the mass of the structure is mostly concentrated in the upper deck structure. Damage to local members progressively leads to the collapse of the entire structure under the influence of gravity. We performed nonlinear pushover analysis on the defect structure after removing each member by using the conventional encountered ice condition as an environmental factor. The importance of each member is evaluated by the obtained component importance index; weak paths caused by different first-to-fail members were analyzed to determine the weakest path in the structure and the location of the starting member in said path. Then, the weak path of the structure was regulated by adjusting the cross sections of a few members on the basis of the component importance index under the condition of constant total steel mass. The main achievements are as follows: effective identification of structural weak paths by component importance analysis, regulation of the weak path by adjusting the starting member in the path, and 10% increase in the ultimate bearing capacity of the structure accompanied by a 10% decrease in the ultimate deformation.

Keywords：jacket platform; pushover analysis; component importance index; plastic development path; weak section

网络出版日期：2016-01-27.

杨飏(1975-) 女，副教授，硕士生导师.