大数据背景下我国上证50ETF期权定价研究
2016-08-03周玉琴朱福敏
周玉琴 朱福敏
(1.西南财经大学,四川成都 611130;2.深圳大学,广东 深圳518060)
大数据背景下我国上证50ETF期权定价研究
周玉琴1朱福敏2
(1.西南财经大学,四川成都 611130;2.深圳大学,广东 深圳518060)
为分析我国上证50ETF期权标资产价格隐含分布特点,在标的资产价格分别服从IHS分布、Weibull分布和对数正态分布假设基础上,对其定价及预测,并运用数据挖掘中机器学习方法修正以上参数模型误差(参考模型方法),进一步与机器学习期权定价中的直接方法和层叠方法比较。实证结果表明,参考模型方法优于其他两种方法,较之支持向量机、神经网络和Boosting算法,随机森林算法可有效预测欧式看涨期权价格,但针对不同价值区间和到期日,标的资产价格隐含分布特点不一致。
IHS分布;随机森林;参考模型方法;价值区间
一、引言
上证50ETF期权上市标志我国金融市场迎来首只场内期权产品,为投资者开展风险管理提供有力工具,准确计算价格并预测未来价格有助于投资者有效决策。此外,大数据时代背景下,如何运用数据挖掘提高期权价格预测精度对风险管理至关重要。Black和Scholes[1]在假设标的资产价格服从对数正态分布基础上推导出欧式期权定价公式,并广泛应用,但因无法解释波动率微笑而受到诸多质疑。为解决此问题,学者改变对数正态分布假定以对期权定价,如McDonald等[2]推导GB2 (Generalized Beta of the Second Kind)分布下的期权定价公式,Mauler等[3]在其他研究基础上,进一步比较各分布下期权定价误差,实证结果表明IHS(Inverse Hyperbolic Sine)分布下的期权定价公式最优,并且其参数校准时间成本小于其他参数超过两个的分布,因此本文选择标的资产价格服从IHS分布假定下的期权定价公式对上证50ETF看涨期权定价,并比较两个参数的Weibull[4]和对数正态分布,探讨上市初期上证50ETF期权标的资产价格隐含分布,有利于市场情绪测量以及相关前瞻信息传播[5]。
期权价格受诸多因素影响,包括标的资产价格、执行价格、资产价格波动率、利率、到期时间、投资者对市场态度和市场趋势等[6]。但基于以上因素以及无套利假设参数期权定价方法依赖于标的资产价格及其波动率[7],并对价格过程严格假定,这些假设与现实不符导致定价系统性误差和套利误差[8]。因此,参数期权定价准确率取决于能否准确反映潜在资产价格过程[9],然而参数定价公式很难反映波动率的时变性与价格随机性特征,对此,数据挖掘中机器学习方法作为非参和半参方法应用于期权定价中。
为降低期权定价误差,提高预测精度,Hutchison[10]首先将神经网络算法引入欧式期权定价模型中,Liang等[6]在前人研究基础上将机器学习下的期权定价方法总结为直接方法(direct method)、参考模型方法(model-reference method)和层叠方法(cascade method),并结合二叉树模型、有限差分模型和蒙特卡洛模拟探讨层叠方法。此外,诸多文献[11-13]分别讨论直接方法和参考模型方法,结果表明神经网络算法和支持向量机算法下的期权定价优于BS模型,Park等[14]进一步研究表明,较之Heston模型和Merton模型,支持向量机算法下的期权定价误差更小。
然而,现有文献仅单独讨论其中一种方法,并通过改进算法提高期权定价及预测精度,但何种方法在期权定价中表现更优以及如何体现三种方法优劣,尚无深入探讨。此外,机器学习包含诸多算法[15],相对其他算法(随机森林、Boosting),支持向量机算法和神经网络算法下的期权定价是否更优?本文基于标的资产价格分别服从IHS分布、Weibull分布和对数正态分布假设,探讨上证50ETF看涨期权标的资产价格隐含分布特点,并结合机器学习方法对其定价及预测,首次运用随机森林算法修正参数期权定价误差,并实证比较三种方法下的期权定价预测精度。
二、理论模型
(一)隐含分布特点
自BS模型提出以来,关于资产价格服从对数正态分布的假设不断改进,如Mauler等[3]、Savickas[4]分别推导出标的资产价格服从IHS分布和Weibull分布的期权定价公式。在风险中性概率测度假设下,状态价格密度函数和期权价格间具有极简单关系(式1),其中C为看涨期权的价格,r为无风险利率,T为距离到期日时间,K为期权执行价格,S为期权合约标的资产价格,f(s)为风险中性概率测度下的标的资产价格密度函数。
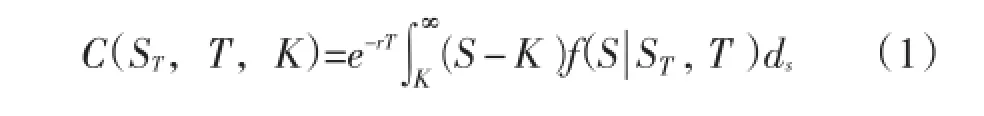
Johnson[16]首先提出IHS分布,IHS随机变量YIHS可表示为式(2),其中sinh为双曲正旋函数,Z为标准随机正态变量,a、b、λ和k分别是与YIHS均值、方差、偏度和峰度相关参数。定义XIHS=S/ST,假设XIHS服从IHS分布,将XIHS带入式(1)中,则欧式看涨期权定价公式为式(3),其中φ-1()为式(2)中的逆函数,Φ()为标准正态分布的累计分布函数。为使得期权价格服从风险中性假设,式(3)中参数需满足约束条件式(4)。

对数正态(LN)分布和Weibull分布假定下的看涨期权定价公式为式(5)[2],其中ψ()表达式分别为式(6)和式(7),CDFLN()为对数正态分布累计分布函数,式(8)中的F[]为合流超几何分布(confluent hypergeometric distribution)。将各分布下的期权定价模型作为参考模型方法和层叠方法中的参数模型,并运用非线性最小二乘方法对式(9)(PK为期权市场价格,CKθ为模型估计价格)校准,进而分析期权标的资产价格隐含分布特点。

(二)机器学习方法
机器学习方法可以从样本数据中找出某种规律[17],广泛应用于对统计数据的回归与分析中,虽在医学、生物信息学、农学等众多领域广泛应用[18-19],但在期权定价中,只应用了支持向量机和神经网络,在此基础上引入随机森林和Boosting算法予以比较。
1.支持向量机。支持向量机(SVM)以增强幻化能力为目标,是Vapnik[20]等于1995年建立的新机器学习算法,采用结构风险最小化(SRM)准则,通过满足Mercer条件的核函数把输入空间数据转换到高维Hilbert空间。给定数据集为L={(Xi,Yi),i=1,2,…,n},其中n为样本总数,式(10)为线性回归函数,其中φ(x)为非线性函数,w和b为函数向量回归参数。支持向量机回归模型(ε-SVM)通过“ε不敏感”误差度量,即损失函数,使回归函数尽量平滑,同时使输入样本对应目标值和求出的输入样本输出值差不超过ε。则SVM优化问题表示为式(11),其中松弛因子ξ和ξ*为引入参量,表示样本超过精度ε程度,取值采用ε不灵敏函数,C是控制超出误差样本惩罚程度的惩罚系数。
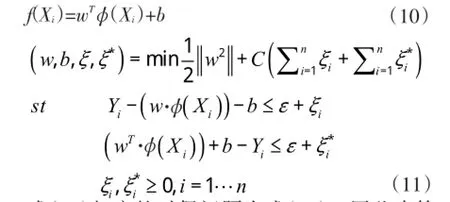
式(11)相应的对偶问题为式(12),因此决策函数为式(13),其中K()为核函数,采用核函数径向基核函数(RBF)(式14)作为SVM定价模型核函数。

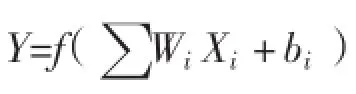

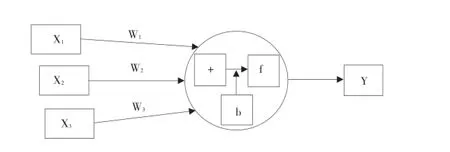
图1 人工神经元模型


图2 随机森林算法

(三)期权定价
学者将机器学习方法(如神经网络和支持向量机)引入期权定价中,由于其假设条件较少,可用未知函数估计,能够较好描述期权价格影响因素与期权价格间非线性关系,预测精度较之传统参数模型(如BS模型)颇为理想。机器学习下的期权定价框架主要包括三种:直接方法(见图3)、层叠方法(见图4)和参考模型方法(见图5)[6],其中直接方法仅运用机器学习方法对期权定价,未结合参数模型[26],而层叠方法和参考模型方法充分结合传统参数模型和机器学习方法优点,即在传统参数模型基础上借助机器学习方法进一步提高期权定价和预测精度[27-28]。

图3直接方法

图4层叠方法
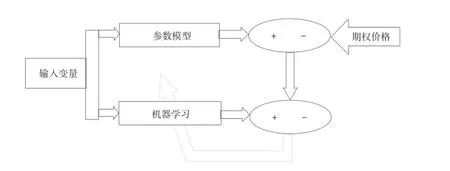
图5 参考模型方法
从三个分布下的期权定价公式可知,影响期权价格因素包括无风险利率、期权执行价格、到期时间、波动率和标的资产价格。Bakshi[29]和Gradojevic[30]建议将期权按价值区间和到期时间分类,因此本文将看涨期权按价值区间(标的资产价格(S)/期权执行价格(K))分为三类,分别为价内期权(ITM;S/K≥1.03)、平价期权(ATM;S/K∈(0.97,1.03))和价外期权(OTM;S/K<1.03);按到期日(T)也分为三类,分别为短期到期期权(T≤60天)、中期到期期权(T∈(60,180)天)和长期到期期权(T≥180天)。因此,在运用机器学习方法时,直接方法输入变量为钱性值(或标的资产价格和执行价格)、波动率、到期时间、无风险利率,目标变量为期权价格;层叠方法输入变量为三个分布下的期权定价结果,目标变量为期权价格;参考模型方法的输入变量与直接方法一致,但目标变量为各分布下的期权定价误差(即期权价格与各分布下的定价结果之差)。
(四)模型评价指标
为比较各模型间期权定价误差及预测精度,通过均方根误差RMSE(Root Mean Square Error)(式18)、平均绝对误差MAE(Mean Absolute Error)(式19)和均方根相对误差RMSRE(Root Mean Square Relative Error)(式20)统计指标评估定价结果和真实价格间误差,其中,N为样本数量,Cmrkk为实际期权价格,Cmodk为模型估计期权价格。


三、数据与实证分析
(一)数据预处理
数据集选取2015年2月至2015年9月交易中的上证50ETF看涨期权,包含31个执行价合约。为稳定定价,剔除距到期日时间少于一周以及期权价格小于0.05的期权合约[26],剩余看涨期权样本3933个,并随机抽取80%(3164)样本作为机器学习训练集,剩余20%(787)为预测集。本文将期权合约买卖平均价作为期权市场价格,上证50ETF前日收盘价作为标的资产当日价格,对应期限的shibor利率作为无风险利率,分别采用标的资产收益率历史波动率(式21)和GJR-GARCH条件波动率(式22和式23)作为波动率参数(见图6),所有数据来源于彭博数据库。从图6可知,上证50ETF收益率历史波动率波动幅度明显小于GARCH条件波动率,运用在机器学习下的期权定价误差进行比较。从样本期间内期权价格描述统计(见表1)可知,我国目前交易中平价期权较少,多属于价内期权;短期期权较少,多属于中期期权,并且价内期权价格均值和波动率均明显高于价外期权和平价期权,短期期权价格均值和波动率明显低于中期期权和长期期权。

图6 上证50ETF收益率波动率时序
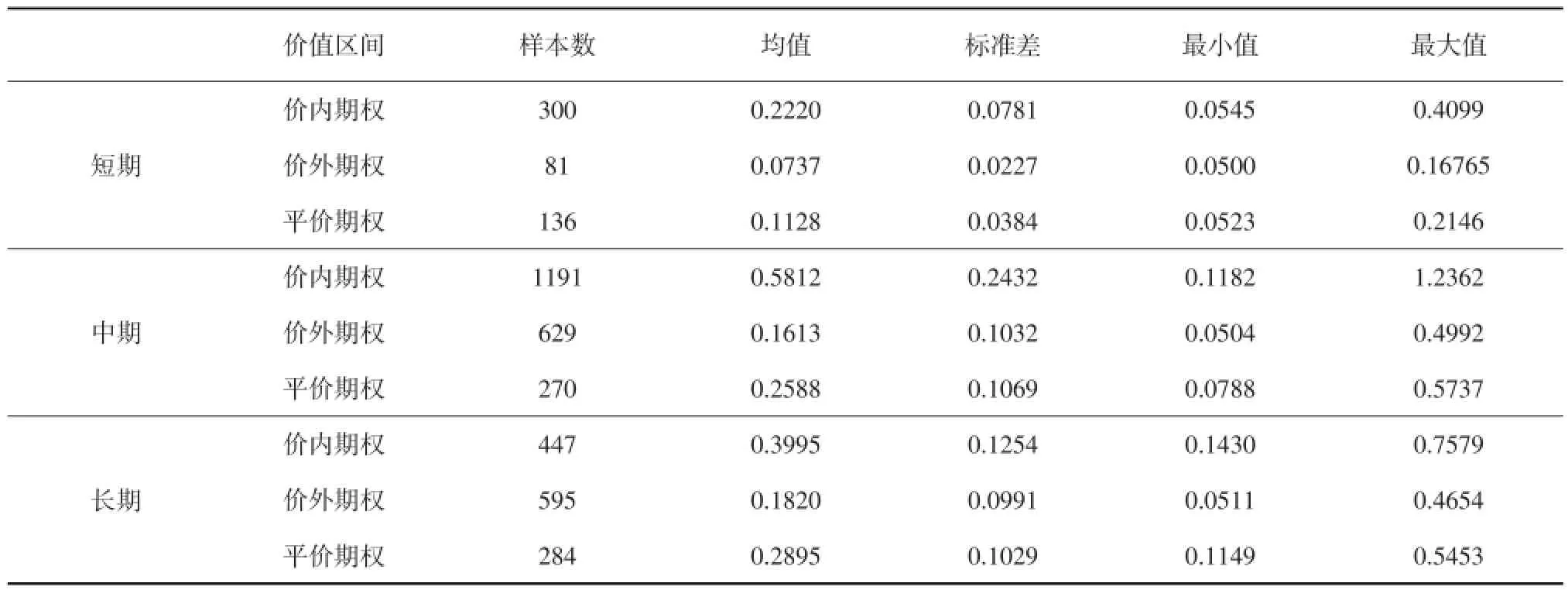
表1 期权价格描述统计
(二)隐含分布特点
为探讨初上市上证50ETF期权隐含分布特点,通过训练集数据校准得IHS分布(a=0.976,b= 0.004,λ=-0.876,k=0.341)、Weibull分布(α= 7.8699,β=1.0930)和LN分布(u=0.380,σ=0.248)的隐含参数,并以此对预测集数据期权定价(见表2),结果表明对数正态分布下的期权定价公式更适合价内期权和平价期权定价,而对于价外期权,IHS分布最优,由于上证50ETF期权初步发展,这与Mauler[3]、Savickas[4]研究结果不符。相较而言,对数正态分布和Weibull分布对价内期权定价误差小于对其他期权定价误差。从不同到期日期权定价预测精度看(见图7),短期期权更适合在IHS分布下定价,而中期期权和长期期权在LN分布下定价预测精度最高,因此在对期权定价时,应针对不同价值区间、不同到期日采取不同定价模型。总体观之,IHS分布下各价值区间期权定价误差差距较小,相对稳定,而Weibull和LN分布对OTM期权定价误差均较大,说明价值区间对Weibull和LN期权定价误差影响较大,但从RMSRE指标可以看出,三个分布下的期权定价效果不佳,需进一步改善,引入机器学习方法修正三个分布下的期权定价误差。
(三)参考模型方法
分别运用随机森林、Boosting、神经网络(隐含层神经元个数为5,迭代次数为200)和支持向量机算法修正上述三种分布下的期权定价误差,即运用参考模型方法对看涨期权定价。根据随机森林修正下不同输入变量的期权定价误差(见表3)可知,运用价值区间变量代替标的资产价格和执行价两个变量作为输入变量的定价误差普遍更小,而不同波动率之间的定价误差较接近。总体而言,随机森林修正后的期权定价误差大幅降低,与其他研究[6]结果一致,但其中经随机森林算法修正后Weibull分布下的期权定价RMSRE降低最多,表明对价外期权而言,Weibull分布优于其他分布,LN分布下的价内期权和平价期权定价误差依然相对较小,而经随机森林算法修正后的IHS分布的RMSRE降低幅度明显低于其他两个分布,说明最优参数期权定价模型经过随机森林修正后期权定价预测精度未必最佳。
由于投资者更关注预测集定价误差,仅给出不同到期日预测集在不同输入变量下的期权定价误差(见图8),结果表明,虽然不同到期日下的期权定价误差均降低,但三个分布下的短期期权定价预测精度较差,经随机森林算法修正后对数正态分布下的短期期权定价预测精度较高,而对于中长期期权,经随机森林修正后Weibull分布下的期权定价误差最小。
分别运用随机森林、支持向量机、神经网络和Boosting算法修正三个分布下的期权定价误差,其中输入变量集与模型5一致。结果表明(见表4和图9),神经网络算法并未达到修正效果,定价误差较大,随机森林修正效果最优,定价误差最小,但对预测集中短期期权定价预测精度需进一步提高,而对中长期期权定价误差较小,其中经机器学习修正后Weibull分布下的期权定价预测结果优于其他两个分布。

表2 各分布下不同价值区间期权定价误差

图7不同到期日分布预测集期权定价误差(MAE和RMSRE)
(四)直接方法和层叠方法
通过随机森林、支持向量机、神经网络和Boosting算法分别对输入变量集直接学习进而对期权定价(直接方法),结果表明(见表5),总体而言,随机森林算法修正下的期权定价预测结果最好,而Boosting算法下的期权定价误差最大;机器学习算法修正下的价内期权定价误差小于平价期权小于价外期权,长期期权定价预测结果优于中期期权优于短期期权;从输入变量集看,对于不同算法,最优输入变量集不一致,未将波动率纳入输入变量集的模型9和模型10定价误差与其他模型较接近,这也是机器学习算法下的期权定价较之参数模型的优越性之一。较之参数模型而言(见表2),随机森林算法和支持向量机算法下的直接期权定价误差小于三个分布下的期权定价误差,但较于参考模型方法,直接方法期权定价误差较大。
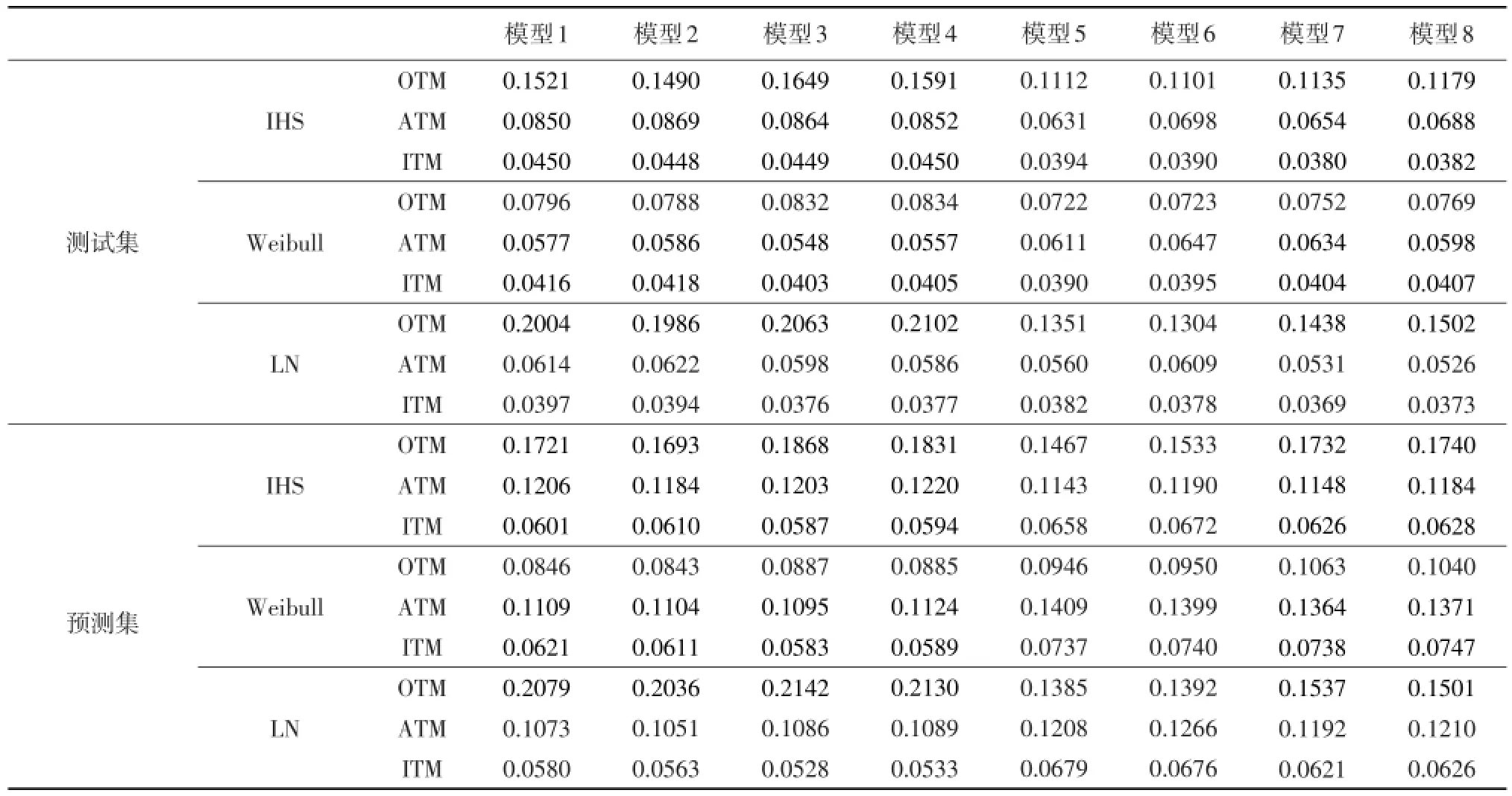
表3 随机森林修正下的不同价值区间期权定价误差(RMSRE)
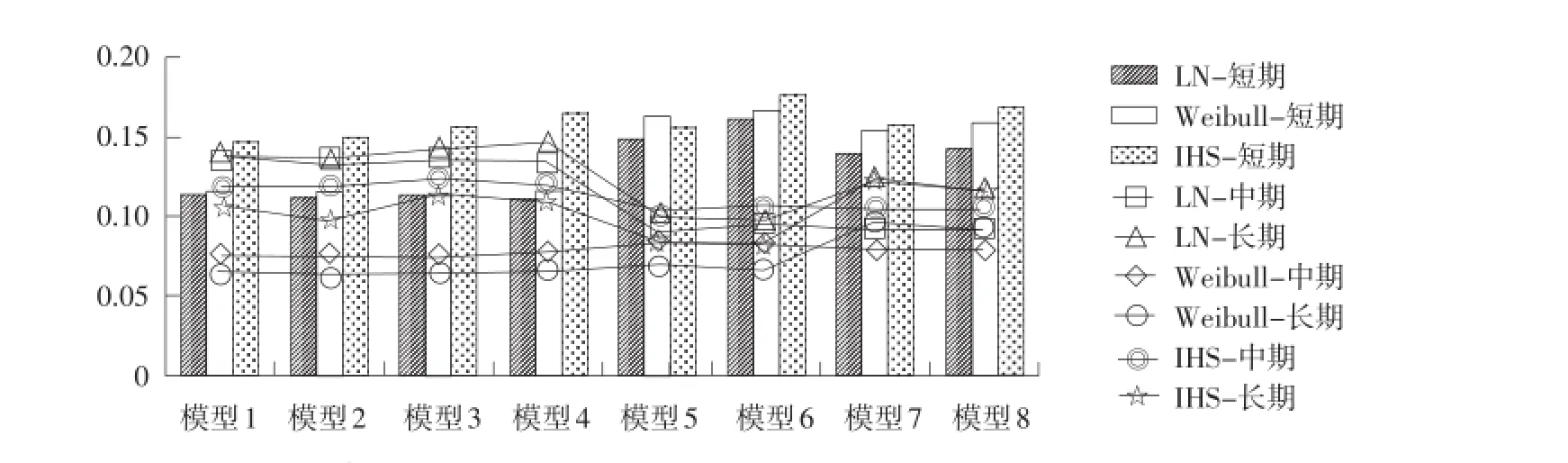
图8 随机森林修正下预测集不同到期日期权定价误差(RMSRE)

表4 机器学习修正下的不同到期日期权定价误差(RMSRE)(模型5)
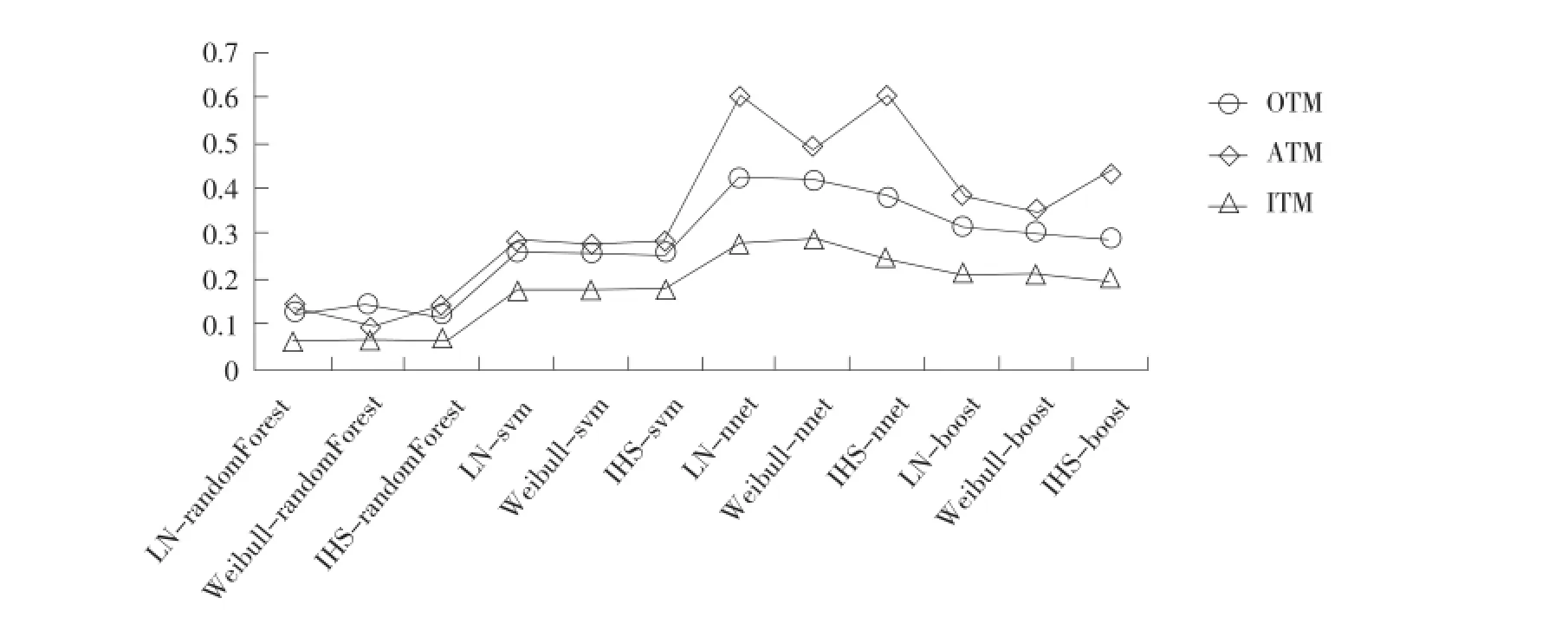
图9 机器学习修正下预测集不同价值区间期权定价误差(RMSRE)
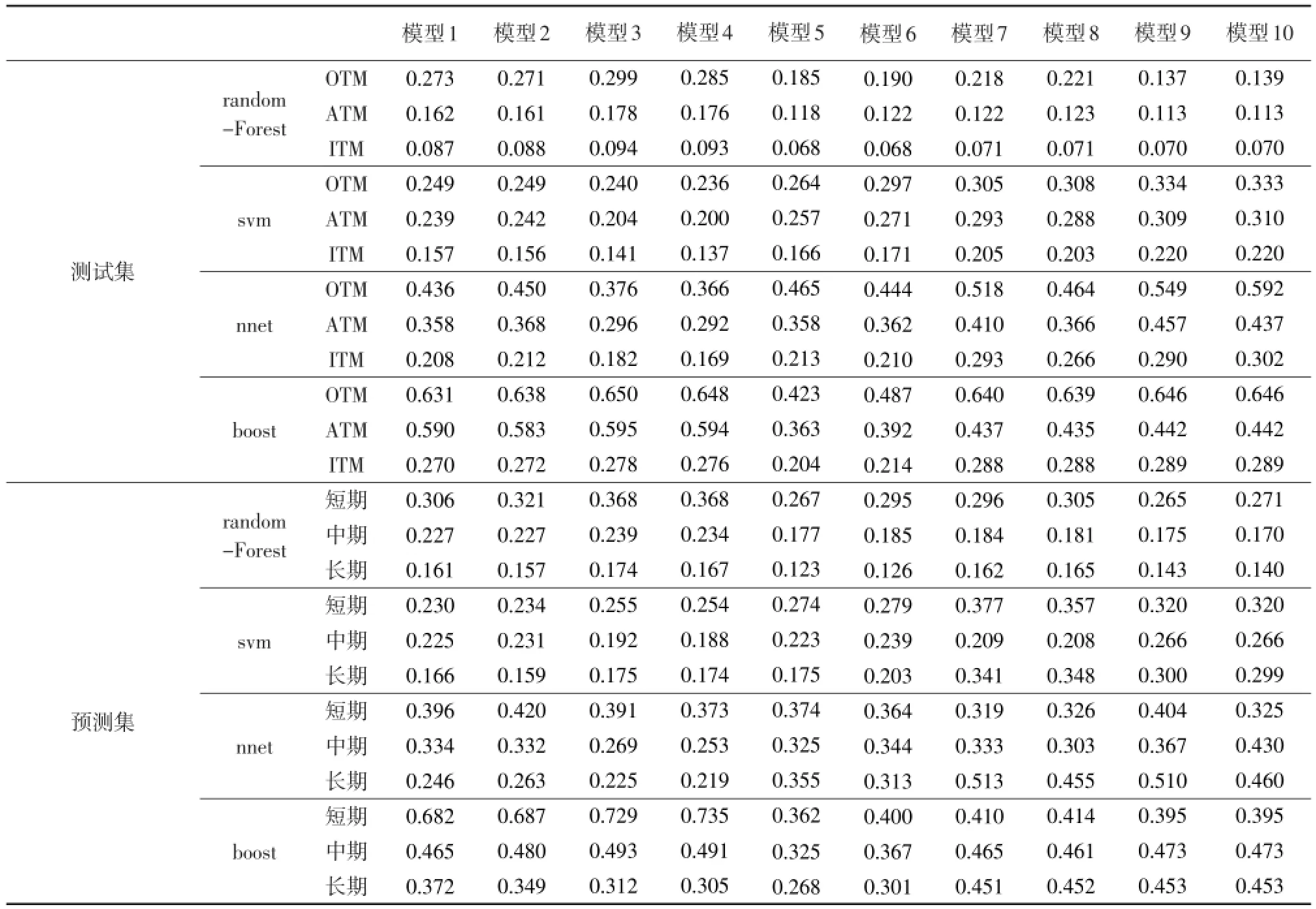
表5直接方法期权定价误差(RMSRE)
通过将三个分布的定价结果作为输入变量开展机器学习对期权定价(层叠方法),结果表明(见表6),较之直接方法和参考模型方法,层叠方法定价误差较大,其中测试集中随机森林算法下的定价误差较小,而预测集中,支持向量机算法下的期权定价预测结果较优,Boosting算法下的期权定价误差极大,尤其对短期期权而言。分别选取各模型中最优者对比,结果表明(见图10),参考模型方法与市场价格最接近,参数模型和层叠方法均高估了价内期权价格,而直接方法低估了价内期权价格。
(五)稳健性检验
为检验期权定价预测结果稳定性,随机抽取40%(1573)和60%(2360)样本作为训练集,剩余样本为预测集,本文仅对参考模型方法加以探讨,结果表明(见表7),减少训练集样本数量并未明显增加期权定价误差,虽然各分布下的期权定价预测结果依然不佳,然而对数正态分布对平价期权和中长期期权,Weibull分布对价内期权以及IHS分布对短期期权的定价误差相对较小,说明参数校准模型对数据样本依赖性不强。不同样本数量训练集下的参考模型方法期权定价结果表明(见表8),训练集占比越高,期权定价误差越小,但相较于参数模型而言,即使仅有40%样本作为训练集的参考模型方法也优于参数模型。
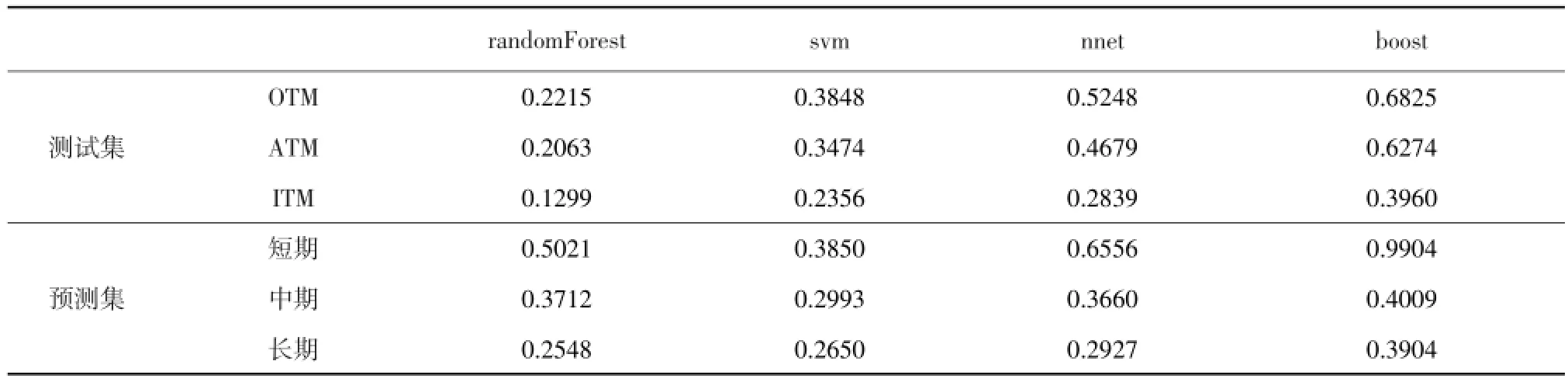
表6层叠方法期权定价误差(RMSRE)

图10 训练集价内期权部分定价结果
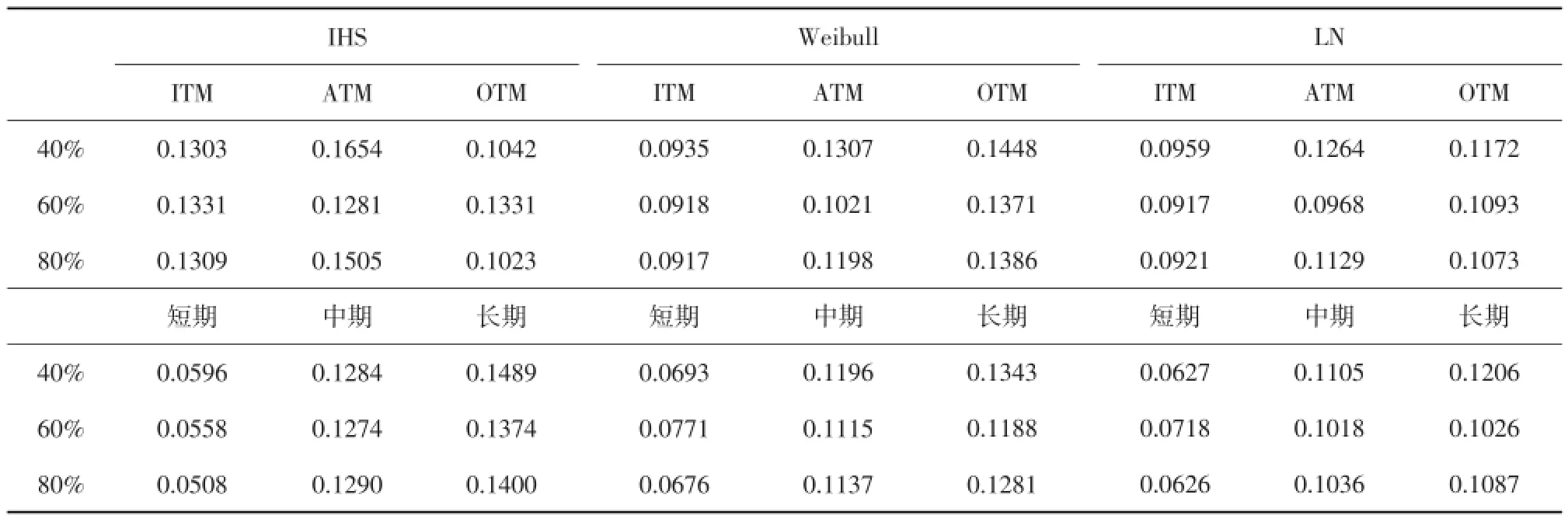
表7 参数模型预测集期权定价误差(RMSE)
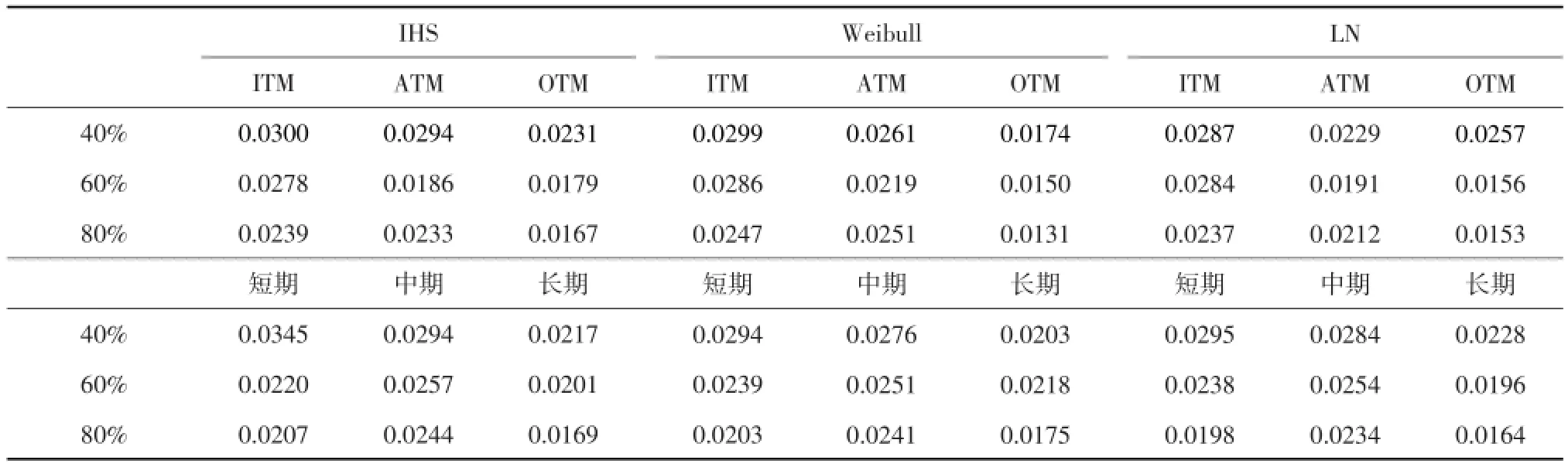
表8 随机森林修正下的预测集期权定价误差(RMSE)(模型5)
四、结论
通过分析我国上证50ETF看涨期权隐含分布特点,比较机器学习算法下的直接方法、参考模型方法和层叠方法对看涨期权定价误差,并对训练集样本展开稳健性检验,结果表明参考模型方法优于直接方法与层叠方法。具体而言,在隐含分布方面,价内期权、价外期权及中长期期权在对数正态分布下的定价预测精度最高,而价外期权和短期期权更适合在IHS分布假定下定价;就机器学习方法而言,相较于支持向量机、神经网络和Boosting算法,随机森林修正下的参考模型方法预测精度最高,其中随机森林修正后Weibull分布下的价外期权和中长期期权定价误差最小,LN分布下的价内期权、平价期权和短期期权定价预测结果最优。由此可知,不同价值区间和不同到期日期权需采用不同模型定价,但均可运用机器学习方法修正误差,有利于提高期权定价预测精度。虽然参考模型方法下的期权定价误差较小,但对短期期权定价预测精度较低,后续将改进随机森林算法,结合其他参数模型进一步提高期权定价预测精度。
[1]Black F,Scholes M.The Pricing of Options and Corporate Liabilities[J].The Journal of Political Economy,1973(3).
[2]McDonald J B,Bookstaber R M.Option Pricing for Generalized Distributions[J].Communications in Statistics-theory and Methods,1991(12).
[3]Mauler D J,McDonald J B.Option Pricing and Distribution Characteristics[J].Computational Economics,2015(4).
[4]Savickas R.A Simple Option-Pricing Formula[J].Financial Review,2002(2).
[5] Bahra B.Implied Risk-neutral Probability Density Functions from Option Prices∶Theory and Application[R].London∶Bank of England Working Paper,1997.
[6]Liang X,Zhang H,Xiao J,et al.Improving Option Price Forecasts withNeuralNetworksandSupportVectorRegressions[J]. Neurocomputing,2009(13).
[7]Bates D S.Empirical Option Pricing∶A Retrospection[J].Journal of Econometrics,2003(1).
[8]Cont R,Da Fonseca J.Dynamics of Implied Volatility Surfaces[J]. Quantitative Finance,2002(1).
[9]Jozef B,Baruníková M.Neural Networks as Semiparametric Option Pricing Tool[J].Bulletin of the Czech Econometric Society,2011(18).
[10]Hutchinson J M,Lo A W,Poggio T.A Nonparametric Approach to Pricing and Hedging Derivative Securities via Learning Networks [J].The Journal of Finance,1994(3).
[11]Garcia R,Gencay R.Pricing and Hedging Derivative Securities with Neural Networks and a Homogeneity Hint[J].Journal of Econometrics,2000(1).
[12]Spreckelsen C,Mettenheim H J,Breitner M H.Real-time Pricing and Hedging of Options on Currency Futures with Artificial Neural Networks[J].Journal of Forecasting,2014(6).
[13]张鸿彦,林辉.应用混合神经网络和遗传算法的期权价格预测模型[J].管理工程学报,2009(1).
[14]Park H,Kim N,Lee J.Parametric Models and Non-parametric Machine Learning Models for Predicting Option Prices∶Empirical Comparison Study over KOSPI 200 Index Options[J].Expert Systems with Applications,2014(11).
[15]Kew W,Mitchell J B O.Greedy and Linear Ensembles of Machine Learning Methods Outperform Single Approaches for QSPR Regression Problems[J].Molecular Informatics,2015(9).
[16]Johnson N L.Systems of Frequency Curves Generated by Methods of Translation[J].Biometrika,1949(1).
[17]Berenji H R.Computational Intelligence and Soft Computing for Space Applications[J].IEEE Aerospace and Electronic Systems Magazine,1996(8).
[18]冯颖,周晓剑.基于机器学习的寿险精算生命表函数估计[J].系统工程,2014(10).
[19]Fantazzini D,Figini S.Random Survival Forests Models for SME Credit Risk Measurement[J].Methodology and Computing in Applied Probability,2009(1).
[20]Vapnik V N.The Nature of Statistical Learning Theory[M].New York∶Springer-verlag,1995.
[21] Brian D.Ripley.Pattern Recognition and Neural Networks[M]. New York∶Cambridge University Press,1996.
[22]Breiman L.Random Forests[J].Machine Learning,2001(1).
[23] Rodriguezgaliano V F,Chicarivas M.Evaluation of Different Machine Learning Methods for Land Cover Mapping of a Mediterranean Area Using Multi-seasonal Landsat Images and Digital Terrain Models[J].International Journal of Digital Earth,2014(6).
[24]Valiant L G.A Theory of the Learnable[J].Communications of the ACM,1984(11).
[25] Friedman J H.Greedy Function Approximation∶A Gradient Boosting Machine[J].Annals of statistics,2001(5).
[26] Amilon H.A Neural Network versus Black-scholes∶A Comparison of Pricing and Hedging Performances[J].Journal of Forecasting,2001(4).
[27] Lajbcygier P R,Connor J T.Improved Option Pricing Using Artificial Neural Networks and Bootstrap Methods[J].International Journal of Neural Systems,1997(4).
[28]王平,王垣苏,黄运成.支持向量回归方法的跳跃扩散汇率期权定价[J].管理工程学报,2011(1).
[29]Bakshi G,Cao C,Chen Z.Empirical Performance of Alternative Option Pricing Models[J].The Journal of Finance,1997(5).
[30]Gradojevic N,Gençay R,Kukolj D.Option Pricing with Modular Neural Networks[J].IEEE Transactions on Neural Networks,2009(4).
F224
A
1672-3805(2016)03-0020-12
2016-04-23
国家自然科学基金项目“基于商品价格联动视角的多商品期货定价研究:中国市场的实证”(71471119);教育部社科研究基金规划项目“网络舆论、市场效应与金融稳定机制创新”(12JJD790026);中国金融发展与金融安全协同创新中心基金项目“基于经济结构协调的金融危机预警研究”(JRXT201601)
周玉琴(1990-),女,西南财经大学金融智能与金融工程四川省重点实验室博士研究生,研究方向为金融风险管理、金融工程。
