改进的特征值灵敏度在结构损伤识别中的应用*

邱飞力，　张立民，　张卫华

(西南交通大学牵引动力国家重点实验室　成都，610031)



改进的特征值灵敏度在结构损伤识别中的应用*

邱飞力，张立民，张卫华

(西南交通大学牵引动力国家重点实验室成都，610031)

摘要传统的特征值灵敏度分析中忽略了振型变化的影响，导致特征值灵敏度难以准确地识别出结构损伤。为提高特征值灵敏度的准确性，利用未损伤结构的振型线性表示损伤情况下结构振型的变化，进而改进了特征值灵敏度的理论分析方法。在不同的损伤工况下，计算数值模型改进前后的特征值灵敏度，验证表明改进后的特征值灵敏度具有更高的精度。以孔洞直径和位置均未知的实际结构为研究对象，利用改进后灵敏度方法准确识别了结构损伤的位置和程度，与结构的孔洞直径和位置实测值相吻合，表明了改进后灵敏度方法具有准确实用性，从而弥补了传统特征值灵敏度法在结构损伤识别中的缺陷。

关键词改进的灵敏度; 特征值灵敏度； 损伤识别； 振型改变

引言

在建筑、机械等结构中往往存在损伤，损伤将影响结构的正常工作甚至导致完全失效[1]。目前在结构损伤识别方面已有大量的研究和应用[2]，多依据结构的模态测试结果，其目标量可分为以下三类：振动时域数据、频域数据和模态参数[3]。由于模态频率测试简单，因此基于模态频率的损伤方法应用较为广泛[4]。然而，结构损伤引起模态频率的变化细微，测试误差、环境因素变化均会导致模态频率变化。当测试及环境因素引起的误差大于等于结构损伤引起的模态频率变化时，其损伤信息将被误差所掩盖而无法识别[5]。

为改善模态频率的不足，引入模态振型变化量。对于结构的局部损伤，模态振型的变化较模态频率更为灵敏[6]。但结构损伤对低阶模态振型不灵敏[7]，且测点数目限制了模态振型测试的准确性[8]。结构的模态特征值与模态频率一样测试简单，却对结构损伤更为灵敏，研究表明结构特征值是一种比较好的动力目标[9]。基于参数灵敏度矩阵的损伤识别方法，通过线性方程组表征模态特征值的改变，却忽略了振型形态的变化[10]，导致灵敏度分析存在误差，进而影响结构损伤识别的准确性[4]。Lee等[11]对结构模态振型改变量测试方法进行了研究。Bicanic等[12]提出应用结构的振型向量表示其变化量，利用损伤结构的模态频率、刚度矩阵扰动和模态振型自身的改变量来表达模态振型的灵敏度参与因子，但该方法方程包含的未知数过多。

为此，笔者提出一种更简洁的方法，将损伤结构振型变化表示为未损伤结构振型的线性组合，使得灵敏度矩阵中包含模态振型的改变，且无需知晓损伤结构的振型，不增加测试工作量，其未知数仅为结构的刚度参数，数目较少。

1灵敏度方法

1.1特征值改变量对比

未损伤结构的模态频率为fi，系统的特征值为λi，则有

(1)

结构损伤引起的频率改变率为bi<0，损伤后模态频率为

(2)

将式(2)代入式(1)可得

(3)

系统的特征值相对改变量，如式(4)所示

(4)

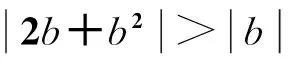
1.2传统特征值灵敏度

系统的模态特征方程可以表示为

(5)

其中：Kn×n和Mn×n分别为结构的刚度矩阵和质量矩阵，n为结构的自由度数；λi为系统的第i个特征值；φi为系统的第i阶模态振型。

结构损伤对结构刚度矩阵的改变量用ΔK表示，并假设损伤不影响结构的质量矩阵。结构的特征值和特征向量改变量分别表示为Δλi和Δφi，其特征方程为

(6)

(7)

忽略结构损伤对模态振型向量的影响，即令式(8)成立

(8)

则式(7)可以改写为如下形式[13-14]

(9)

舍弃的方程(8)部分，将影响灵敏度矩阵的精度，进而导致结构损伤识别不准确。

1.3改进的特征值灵敏度

为解决灵敏度方法的不足，获取更准确的特征值灵敏度，引入模态振型变化。对特征方程(5)两边同时求导并移项得

(10)

其中：dφi为i阶模态振型的改变。

依据结构模态振型的正交性，模态振型的改变可以用结构振型向量的线性组合表示如下

(11)

其中：aij表示第j阶模态对第i阶模态振型改变的贡献率。

(12)

其中：dK和dM分别为结构刚度矩阵和质量矩阵的改变。

(13)

将方程(11)代入方程(13)，化简可得

(14)

假设结构损伤对质量的改变可忽略，损伤引起各阶振型的改变量为

(15)

式(15)中

(16)

aii=0表明第i阶振型对第i阶振型的变化量参与因子为零。式(7)特征值的改变量可以表示为

改进后的特征值灵敏度计算式如(19)所示

(19)

1.4优化求解

根据结构损伤前后的特征值残差和特征值灵敏度矩阵S建立目标函数，如式(20)所示

(20)

目标函数(20)可以通过信赖域方法求解，设pk为第k次迭代点，J=J(pk)，gk=▽J(pk)。Bk是Hessen矩阵▽2J(pk)的第k次近似，则第k次迭代步的信赖域子问题表达式[15]为

(21)

2特征值灵敏度

2.1灵敏度精度

为研究改进后的特征灵敏度精度，建立两端约束的矩形截面梁。弹性模量为206 GPa，密度为7 800 kg/m3。单元尺寸为0.03 m，截面积为2.2×10-4m2，截面高为46 mm，惯性矩为3.8×10-8m4，有限元模型见图1。

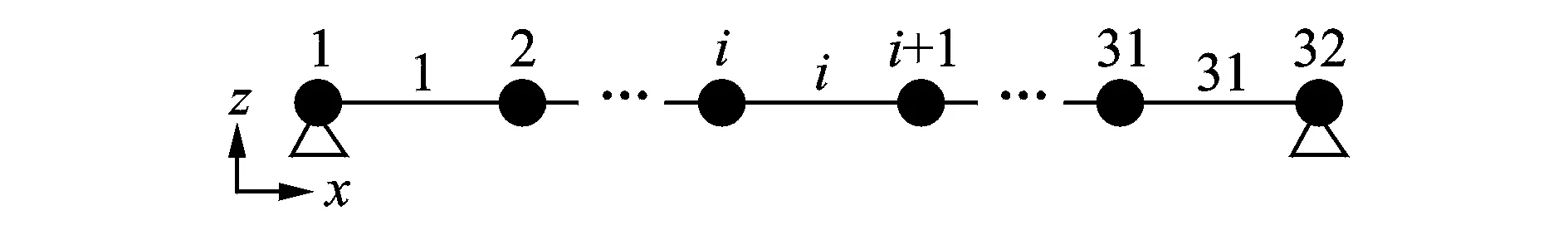
图1　数值有限元模型Fig.1　The numerical FEA model

采用降低模量的方式模拟单元刚度的损伤，数值计算工况如表1所示。

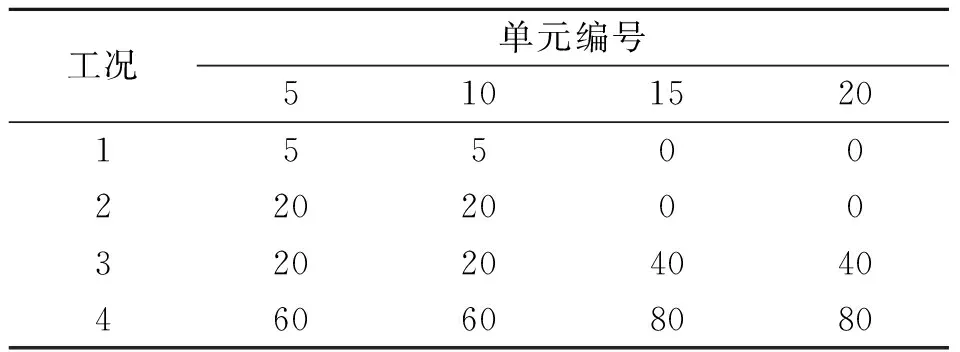
表1　各工况单元模量损伤百分比

为量化改进后的特征灵敏度精度，引入特征值相对误差，如式(22)所示

(22)

绘制结构前7阶特征值灵敏度误差，如图2所示。

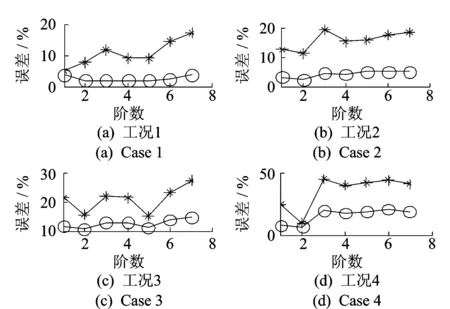
带*标记和小圆圈o标记的曲线分别为传统特征值灵敏度和改进后的特征值灵敏度误差图2　各工况下特征值灵敏度误差曲线Fig.2　The sensitive error curves of eigen values

结合表1和图2，改进后的特征灵敏度方法比传统的特征灵敏度方法更为准确。对比工况1～3，增大刚度损伤程度和增加新的损伤位置，都将增加传统特征灵敏度方法的误差。从工况4可知，结构的刚度损伤程度严重(60%或80%)时，传统灵敏度方法计算的部分阶特征值误差极大(近50%)。

2.2特征值改变量

某矩形长铁片两端约束，其结构上存在3个直径和位置均未知的孔洞，其几何形状如图3所示。

图3结构几何形状图
Fig.3The geometry of the structure

结构的几何参数值如表2。

表2　结构几何参数表

Tab.2　The geometric parameters of the structure　　m

参数长度x宽度y厚度z数值0.9300.0480.004

为消除传感器对结构附加质量的影响，在结构中部布置1个加速度传感器，利用冲击力锤进行模态测试，0～500 Hz内的垂向频响函数如图4所示。

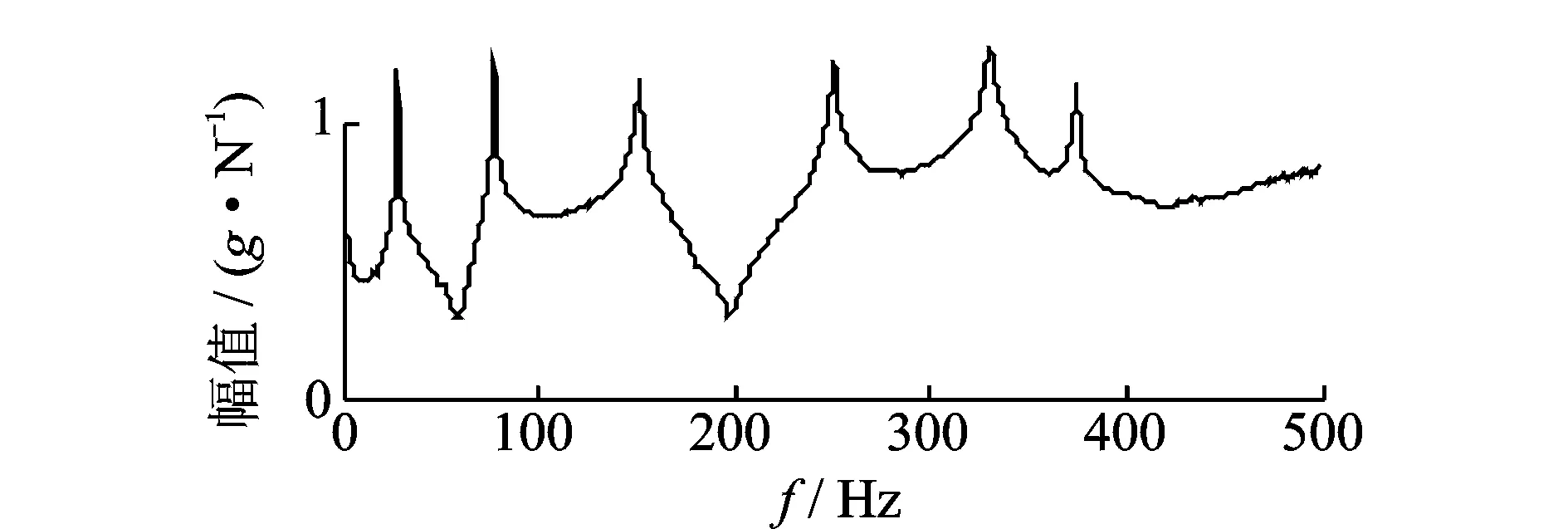
图4　结构综合频响函数Fig.4　The multi frequency function of structure

采用31个大小相等的shell63单元建立有限元模型，有限元模型单元划分如图5所示。

图5有限元网格模型
Fig.5The finite element mesh model

在ANASYS中对模型结构施加两端固定约束，对0～500 Hz内仿真和测试的频率如表3所示。

由表3可知，结构的特征值对结构的局部损伤比模态频率更为灵敏。

表3　模态参数对比表

Tab.3　The comparison of modal parameters

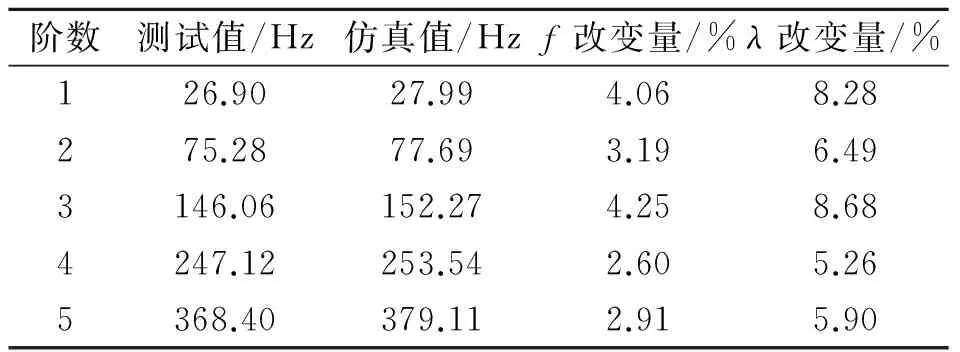
阶数测试值/Hz仿真值/Hzf改变量/%λ改变量/%126.9027.994.068.28275.2877.693.196.493146.06152.274.258.684247.12253.542.605.265368.40379.112.915.90

f，λ分别表示模态频率和模态特征值

2.3特征值灵敏度

以各单元的等效模量损失表示结构的损伤。结合式(19)，对单元模量参数Ei进行特征值灵敏度分析。各Ei对前5阶特征值的灵敏度如图6所示。

图6　各单元模量的特征值灵敏度Fig.6　The eigen value sensitivities of elements modulus

由图6知，单元模量对各阶特征值的灵敏度成起伏趋势，而1～5阶特征值分别对应着结构的前五阶垂向弯曲振型。这表明振型变形最大位置对应的单元模量对该阶模态特征值灵敏度最高。

3损伤识别

利用信赖域方法求解式(20)，目标函数收敛过程如图7所示。从图7可知，目标函数经过10次迭代趋于稳定收敛，识别的各单元模量损伤量用百分比表示如图8所示。

图7　目标迭代收敛图Fig.7　The converge of objective iterations

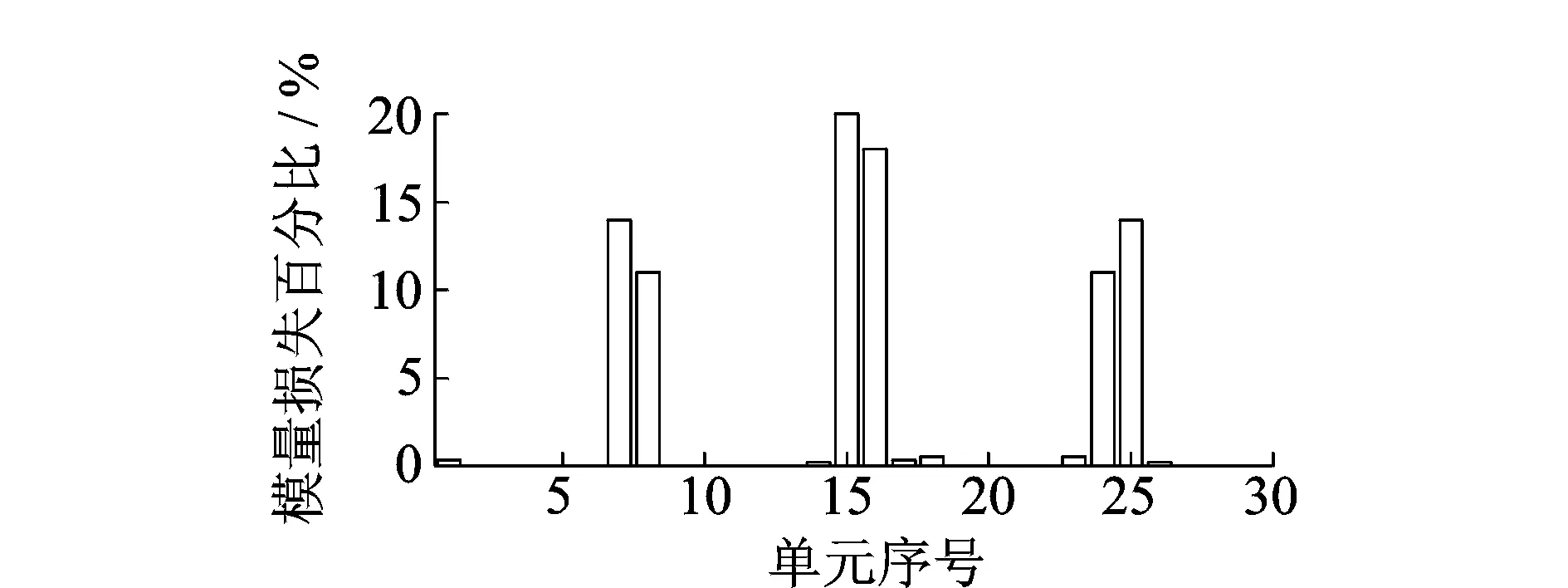
图8　单元等效模量相对损失量Fig.8　The relative damage of element equal modulus

从图8可知，改进灵敏度方法识别的结构损伤位置位于第7和8个单元，15和16单元，24和25单元处。从表2和图5可计算出损伤位置位于x=21.0 cm，x=45.0 cm，x=72.0 cm附近。

为验证改进后灵敏度损伤识别位置的精度，对该结构孔洞位置进行测量，如图9所示。

图9　结构孔洞测量照片Fig.9　The measured of structure holes

从图9可知，结构实际损伤位置与改进灵敏度方法识别的损伤位置相吻合。

利用游标卡尺测量孔洞内径Φ，其结果见表4。

表4　孔洞内径测量结果

Tab.4　The measured results of inner diameters

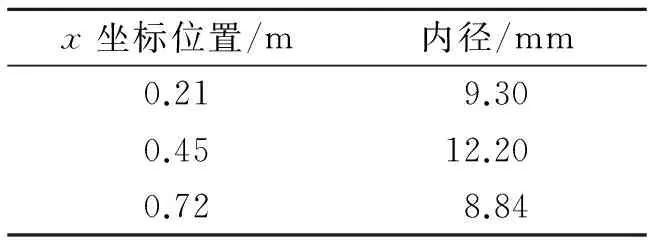
x坐标位置/m内径/mm0.219.300.4512.200.728.84

带有孔洞结构等效模量的实际损伤量[17]可以用式(23)进行计算

(23)

其中：c1为孔洞的体积比率；a=(1+γ)/3(1-γ)，γ为泊松比。

损伤识别值和真实值对比如图10所示。分析图10，传统灵敏度方法结构损伤程度识别的误差较大，且损伤程度越严重其准确性越低。改进的灵敏度方法与实际值比较误差不大于2%，解决了传统灵敏度方法的缺陷。

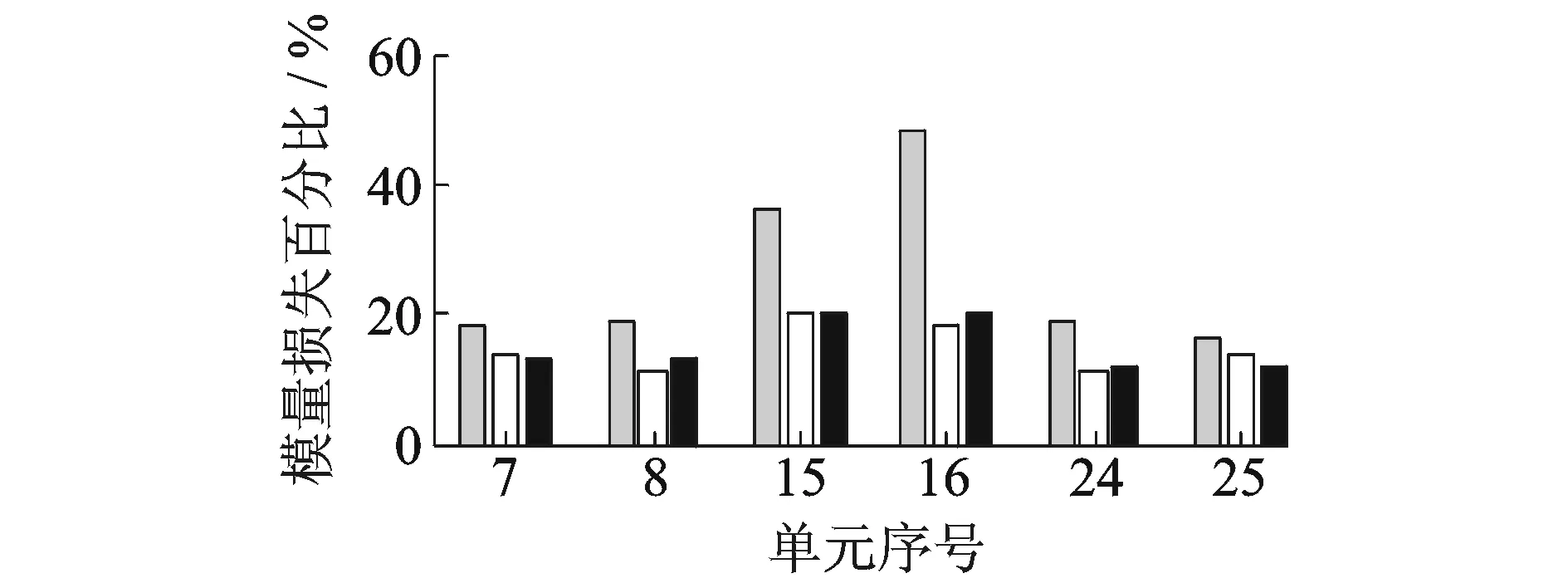
图10　损伤识别值与实际损伤值对比图Fig.10　The comporison of the exact and identified values图中灰色、白色和黑色柱形填充分别为传统方法、改进后方法的损伤识别量和结构真实损伤量。

4结论

1) 在结构损伤相同时，从理论上验证了模态特征值比模态频率对损伤更灵敏，更适合作为损伤识别的目标量。

2) 利用未损伤结构的振型表示损伤前后振型的变化，推导了改进的特征值灵敏度计算方法。通过数值算例验证表明：在不同的损伤工况下，改进的灵敏度方法均比传统灵敏度方法的精度高。

3) 应用改进的灵敏度方法对实际结构进行损伤识别，识别的损伤位置与实际位置相吻合；识别的损伤程度与实际值之差不大于2%，其准确性远高于传统灵敏度方法识别结果，进而解决了传统灵敏度方法损伤识别不准确的缺陷。改进后的方法经过10次迭代收敛，具有实用高效性。

参考文献

[1]Li Jing, Li Zhengguang, Zhong Huixiang, et al. Damage detection using generalized flexibility and changes in natural frequencies[J]. AIAA Journal,2012,50(5):1072-1077.

[2]Chang F K, Mueller I, Lonkar K. Integrated passive active interactive diagnostic technique based on efficient inverse methods for condition monitoring and damage detection for an integrated vehicle health management[R].Califoria: Stanford University, 2008:12-17.

[3]韩红飞,周邵萍,郝占峰，等.基于应变模态差的管道损伤识别仿真[J].振动、测试与诊断,2013,33(S1): 210-213.

Han Hongfei, Zhou Shaoping, Hao Zhanfeng, et al. Study on identif ication of pipe damage based on strain modal difference [J]. Journal of Vibration, Measurement & Diagnosis,2013,33(S1): 210-213. (in Chinese)

[4]Esfandiari A, Bakhtiari-Nejad F, Rahai A. Theoretical and experimental structural damage diagnosis method using natural frequencies through an improved sensitivity equation[J]. International Journal of Mechanical Sciences, 2013,70(5):79-89.

[5]孙晓燕,郑津洋,Huston R D,等.损伤识别在车用储氢容器模态试验中的应用[J].振动、测试与诊断,2014,34(3):379-384.

Sun Xiaoyan, Zheng Jinyang, Huston D R, et al. Experiment modal analysis and damage detetion for automobile hydrogen on-board storage tank [J].Journal of Vibration, Measurement & Diagnosis, 2014, 34(3): 379-384. (in Chinese)

[6]Yia W J, Zhoua Y, Kunnath S, et al. Identification of localized frame parameters using higher natural modes[J]. Engineering Structure, 2008,30(11):3082-3094.

[7]张锋.基于模态的简支梁损伤识别[D].长沙:湖南科技大学,2012.

[8]Sanayei M, McClain J A S, Wadia-Fascetti S, et al. Parameter estimation incorporating modal data and boundary conditions [J]. Journal of Structural Engineering-ASCE,1999, 125(9):1048-1055.

[9]冉志红,屈俊童,和飞.桥梁结构损伤诊断的模式识别理论及其工程应用[M].北京:科学出版社,2011:31-42.

[10]郝占峰.基于曲率模态和优化算法的管道损伤识别研究[D].上海:华东理工大学,2014.

[11]Lee J S, Choi Y, Cho H N. Modeling and detection of damage using smeared crack model [J]. Engineering Structure,2004, 26(2): 267-278.

[12]Bicanic N, Chen H P. Damage identification in framed structures using natural frequencies [J]. International Journal for Numerical Methods in Engineering,1997,40(23): 4451-4468.

[13]朱茂桃,陈亚洲.基于灵敏度方法的车门模态优化[J]. 重庆交通大学学报：自然科学版, 2014, 33(1): 139-144.

Zhu Maotao,Chen Yazhou. Modal optimization of car door based on sensitivity method [J]. Journal of Chongqin Jiaotong University: Natural Science,2014,33(1): 139-144. (in Chinese)

[14]杨英,赵光耀,孟凡亮.某轿车白车身结构灵敏度分析及设计优化[J].东北大学学报,2008,29(8):1159-1163.

Yang Ying,Zhao Guangyao, Meng Fanliang. Structure sensitivity analysis and optimized design of a certain white bodywork [J].Journal of Northeastern University, 2008,29(8):1159-1163. (in Chinese)

[15]Bijaya J S, Ren W X. Damage detection by finite element model updating using modal flexibility residual [J]. Journal of Sound and Vibration, 2006,290:369-387.

[16]马昌凤.最优化方法及其matlab程序设计[M].北京:科学出版社,2010:83-93.

[17]周金将,余绍锋. 等效模量法计算冷弯薄壁开孔槽钢柱屈曲应力[J].科研开发,2010,25(2):27-31.

Zhou Jinjiang,Yu Shaofeng. Equivalent calculation of buckling stress for cold-formed thin-wall perforated column [J]. Stell Construction, 2010,25(2):27-31. (in Chinese)

E-mail: qfl_43@163.com

doi:10.16450/j.cnki.issn.1004-6801.2016.02.009

收稿日期：2015-01-09；修回日期：2015-03-16

中图分类号TH113.1

第一作者简介：邱飞力，男，1987年2月生，博士生。主要研究方向为有限元模型修正。曾发表《基于响应面方法的支架结构模型修正研究》(《噪声与振动控制》2014年第34卷第3期)等论文。

*国家自然科学基金资助项目(U1234208)