顾左右而言他——谈函数问题的间接求解

◇　河北　郝建业



顾左右而言他
——谈函数问题的间接求解

◇河北郝建业

直接思维是我们看到一类问题时,最直观的思考方式,也是最易想到的方式.数学解题中的通法训练,也是对同学们直接思维的培养．但在某些问题的解答中如果直接求解会遇到很多障碍,甚至陷入死胡同．此时如果转换思维间接思考,常可峰回路转、柳暗花明．本文以函数问题为例谈间接法解题的功效．

1　间接判断，避繁求简

Af(x)的图象关于(π,0)中心对称;

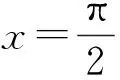
Cf(x)为非奇非偶函数

对于B:若y=f(x)的图象关于直线x=π/2对称,则f(π-x)=f(x).f(π-x)=cos(π-x)·sin 2(π-x)=cosxsin 2x=f(x),故B正确．

对于C:因为cosx为偶函数,sin 2x为奇函数,所以f(x)为奇函数．故C错误．

正确答案为A、B．

2　整体代换，设而不求

图1

Aa>0,b<0,c>0,d>0;

Ba>0,b<0,c<0,d>0;

Ca<0,b<0,c<0,d>0;

Da>0,b>0,c>0,d<0

3　由局部代整体，柳暗花明

ln(a+x2-x2)=lna=0,解得a=1.

4　借助图象，峰回路转

图2　　　　　　　图3　　　　　　　　图4

总之,在相关的问题的求解中要本着“多想少算”的原则,正面求解较为复杂或不易实现时,可转换求解思路,间接寻找解题方向,即可化难为易．

河北丰润车轴山中学)