快递行业配送网点布局规划研究
2016-08-02彭姗姗王丹丹陆克斌罗海星
彭姗姗,王丹丹,陆克斌,罗海星
快递行业配送网点布局规划研究
彭姗姗1,王丹丹1,陆克斌1,罗海星2
(1.安徽新华学院商学院,安徽合肥230088;2.合肥工业大学建筑设计研究院,合肥230009)
在分析快递行业配送网点的布局规划问题的基础上,首先根据最大覆盖模型的思想建立了配送网点布局的覆盖模型,模型以所覆盖的需求最大为目标函数。然后,根据所建立的模型设计了分支定解法进行求解。最后,给出了一个简单的算例来验证了模型和算法的有效性,并进行了简单的总结。
快递;网点布局;最大覆盖模型
0 引言
随着经济及电子商务的飞速发展,快递行业也成为商品流通的主要通道。与此同时,快递业务也成为物流的主要业务领域。在快递业务中,由于快递的时效性,如何确定配送网点以更好、更快地为客户服务已成为一个值得深入研究的现实问题。国内外不少学者就该问题展开了研究,Burwell等[1]认为快递企业网点也存在其商圈,商圈区域以网点为中心,根据网点周边的企业及居民分布,沿着一定的方向和距离向外扩展,但由于快递存在时效性,商圈区域是有限度的。Wilson[2]认为快递业务中也存在着集聚效益,在集聚区有着大量而稳定的快递市场,则必定在此建立快递企业网点。刘海涛[3]定性地分析快递企业网点布局规划问题,并以某公司北京城区快递网点的空间布局为例,总结了网点数量与层级空间分布的最佳形式和一般规律。
Church等[4]提出了最大覆盖模型,并将其应用于应急设施选址问题。该模型不要求所有的应急地点都被覆盖,而是建立特定数目的应急中心,以覆盖尽可能多的人口[5]。快递业配送网点的布局也可以采用最大覆盖模型的思想,在满足特定约束的条件下建立尽可能少的配送网点来覆盖尽可能多的需求点的需求。本文就是基于这样的思想而展开研究的。
1 问题分析
快递企业在建立配送网点时,为了扩展业务及提高服务能力,应以使所建立的网点能满足尽可能多的客户的需求为目标。同时快递公司本身也要从本身的建设成本出发,不能建立无限量多的配送网点,这样将增加自身的固定资产投入,所以快递企业将限制最大的建设投资,从而限制配送网点的建设数目。网点建设好了,每个网点的服务能力是有限的,这就约束了网点的服务量。在快递业中,存在时效性的限制[6],例如,某些快递公司对客户承诺1 h内上门取件等,因此每个网点都有其最大服务半径。只有在配送网点最大服务半径范围内的客户,该配送网点才能为其服务。
为了简化实际问题,在建立模型前做如下假设:
(1)只考虑配送网点的建设费用,不考虑配送网点的可变费用,如人工费用、办公费用、存储费用等。
(2)不考虑区域内交通因素的影响,超过最大服务半径则达不到快件时效性的要求。
(3)假设各个网点之间有业务往来,且能互相服务。
2 配送网点布局的覆盖模型
所谓覆盖模型,就是确定一组服务设施来满足这些需求点的需求,为了达到成本最小,须用最小数量的设施去覆盖尽可能多的需求。在快递业中,由于快件时效性的限制,每个网点都有其最大服务半径,即只能覆盖在最大服务半径内的需求点。模型以所覆盖的需求最大为目标函数,满足建设投资、服务能力、服务范围等约束。
设有M个需求点,从这M个点中决策选择几个点作为配送网点,可建立如下数学模型:
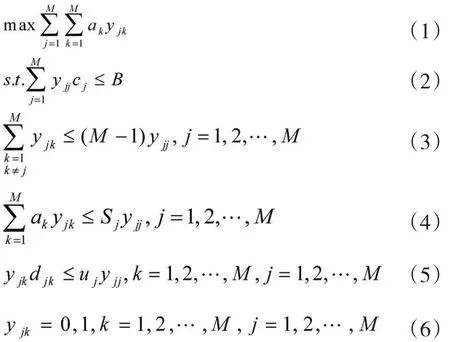
模型中各符号所代表的意义如下:
决策变量:yjj为0~1变量,表示是否在需求点j建立配送网点(1—建,0—不建),若在需求点j建立配送网点则表示其需求被其自身所覆盖。yjk为0-1变量(k≠j),表示需求点j(必须是配送网点)是否覆盖需求点k。
常量:ak为需求点的需求量。cj为在需求点j建立配送网点的建设费用。B为最大总投资。Sj为若需求点j是配送网点时的服务能力。djk为需求点j与需求点k间的距离。uj为若需求点j是配送网点时的最大服务半径。
模型中,式(1)为目标函数,即使总的覆盖的客户需求量最大化。式(2)为约束总的建设成本部超过总投资。式(3)保证了只有被选为配送网点的需求地,才能为其它的需求地服务。式(4)为每个被选为配送网点的需求地的服务能力约束。式(5)为每个被选为配送网点的需求地的最大服务半径约束。式(6)为0-1约束。
3 算法设计
该模型是一个典型的混合整数规划模型,可用分支定界法来进行求解[7]。对于极大化问题,如果在求解前能获得一个较佳(较大)的上界,则可在求解过程中减少分枝数和迭代次数,从而提高求解的效率。结合所建立的模型,可设计如下计算步骤:
Step 1:设定R,令r=1。
Step 2:根据约束条件(2)得出一组新的配送网点组合(求出(yjj)r)。
Step 3:根据Step 2的结果,求解除去约束条件(2)的模型。由于为线性规划,可直接采用Lingo编程[8]进行求解。得到(yjk)r和目标函数值fr,令r=r+1。
Step 4:若r Step 5:以f为下界采用分支定界法求解模型。 Step 6:输出最优解和目标函数值。 某快递公司在某一城区有3个需求地,各需求地之间的距离如表1所示。各需求地的需求量和服务能力如表2所示。 表1 各需求地之间的距离Tab.1Distance between each plot km 各网点的建设费用:需求地1为500元,需求地2为560元,需求地3为540元,最大总投资为700。各网点的最大服务半径:需求地1为200元,需求地2为250元,需求地2为210元。 表2 各需求地的需求量和服务能力Tab.2Demand and service capability each plot 包次 结合所设计的分支定界法,采用lingo编程求解得到最优解为y11=1,y12=1,最优目标函数值为28 842。即在需求地1建立配送网点,该配送网点覆盖需求地1和需求地2的需求。 从计算结果来看,它符合模型中的所有约束条件。该算例是一个非常简单的算法,通过穷举可行解可以看出,所得到的解确实是最优解。这就说明,所设计的分支定界法能够有效地求解所建立的模型。 快递行业配送网点的布局规划是决定快递行业运作成本、服务质量的重要因素。给出可行、优化的配送网点的布局规划方案显得尤为重要。本文通过简单分析快递行业配送网点布局规划问题,提出了依据最大覆盖模型来解决该问题的思想,并建立了相应的以所覆盖的需求最大为目标函数,以最大建设投资、服务能力、服务范围等为约束的数学模型。接着,针对所建立的混合整数规划模型,设计了相应的分支定界法来求解。从给出的一个简单的算例来看,所设计的分支定界法能够有效地求解所建立的模型。该模型和算法具有较高的实用价值,能为快递公司的配送网点的布局规划提供一定的理论依据。 [1]BURWELL,T.H.MCKNEW,M.A.JARVIS.J.P.An Application of a Spatially Distributed Queuing Model to an Ambulance System[J].Socio—Economic Planning Sciences,1992(26):289-300. [2]WILSON.A.G.Geography and the Environment Systems Analytical Methods[M].London:University of California Press,1981. 77-89. [3]CHURCH,R.REVELLE.C.The Maximal Covering Location Problem[J].Papers of the Regional Science Association,1974, 32, 101-118. [4]刘海涛.快递企业城市网点布局与优化研究[D].北京:北京交通大学,2007.21-31. [5]殷代君.广义最大覆盖模型在应急设施选址中的应用研究[D].济南:山东大学,2007.8-12. [6]张兰.快递企业网点布局研究[D].长沙:中南大学,2008.3-10. [7]赵晓煜,汪定伟.供应链中二级分销网络优化设计的模糊机会约束规划模型[J].2002,2(19):249-253. [8]姜启源.优化建模与LINDO/LINGO软件[M].北京:清华大学出版社,2005,44-67. Study on Net Point Layout of Express Delivery Industry PENG Shan-shan1,WANG Dan-dan1,LU Ke-bin1,LUO Hai-xing2 On the basis of the analysis of net point layout of express delivery industry problems,this paper establishes a covering model of net point layout based on the idea of maximal covering model.This model maximizes the covered demand,then,design related branch and bound method to solve it,finally,uses the numerical example to analyze the effectiveness of the model and the algorithm,and a brief summary is given. express;net point layout;maximal covering model F259.23 A 1673-1891(2016)01-0086-03 10.16104/j.issn.1673-1891.2016.01.023 2015-10-10 安徽省高校振兴计划重大项目(2013zytz080);安徽新华学院教育教学研究项目(2015jy019);安徽新华学院专业综合改革试点项目(2015zyzhx02);中国物流学会项目(2013CSLKT141);安徽新华学院重点学科资助项目(ZDFCX 201104)。 彭姗姗(1988—),女,助教,硕士,研究方向:运输与物流。4 算例


5 结语
(1.Business School,Anhui Xinhua University,Hefei,230088,China; 2.Architectural Design Institute,Hefei University of Technology,Hefei,230089,China)
