特解法求解无界弦的受迫振动方程

许湘

特解法求解无界弦的受迫振动方程

许湘

（西华师范大学理论物理研究所，四川南充637009）

一维无界的波动方程，当不考虑外力时典，可通过达朗贝尔公式直接求解。当考虑外力时，不能直接运用达朗贝尔公式求解，但是可以通过叠加原理将方程齐次化，进而求解。特解法能将无界弦的受迫振动方程转化成无界弦的自由振动方程，进而可通过达朗贝尔公式，快速得到结果。

波动方程；泊松公式；达朗贝尔公式

0 引言

有限域在求解泊松方程中有广泛的应用，但是在无界域波动方程，却很少应用。无界弦的受迫振动方程往往采用傅里叶变换法和泊松公式求解，但对于一些简单的问题可以有更简单的方法，特解法就是其中一种。本文通过应用特解法将无界弦的受迫振动方程转化成无界弦的自由振动方程，进而可通过达朗贝尔公式，快速得到结果。

1 无界弦的受迫振动方程求解

对于无界弦的受迫振动方程，这是问题归结于考虑非齐次方程的定界问题

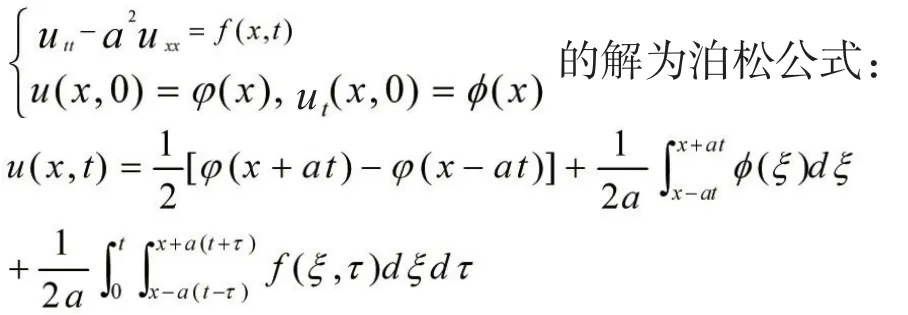
此方法虽然直接，但是需要计算二重积分，有点麻烦。在有些情况下，无界弦的受迫振动方程可以利用特解法和达朗贝尔公式来求解。

由特解法求解受迫振动方程的方法及步骤:(1)观察泛定方程寻求特解.(2)利用叠加原理将非齐次波动方程转化为齐次波动方程.(3)利用达朗贝尔方程得到结果。

2 通过实例说明

例1求解波方程初始

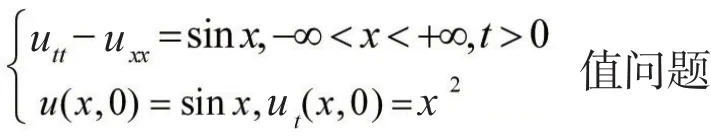
观察泛定方程右边只是x的函数，所以可设w= w(x)，并且满足

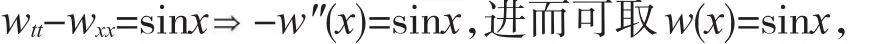
令u（x，t）=v（x，t）+w(x)=v（x，t）+sinx，则v（x，t）满足

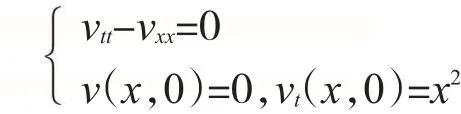
由达朗贝尔公式得

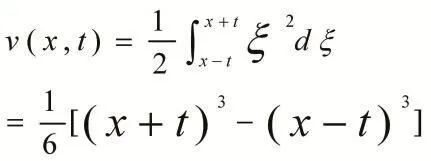
因此原问题的解为：

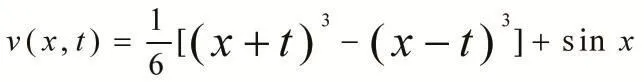
此方法比积分变换法，快速，简洁。例2求解波方程初始值问题

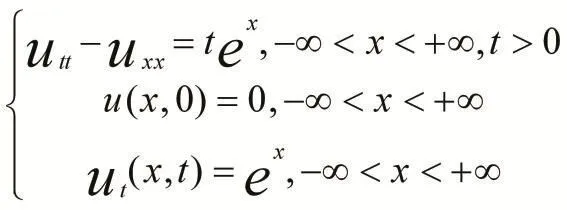
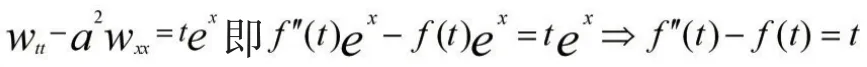
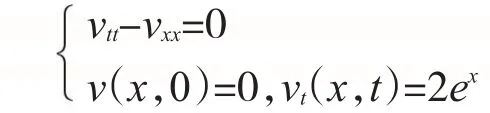
由达朗贝尔公式得：

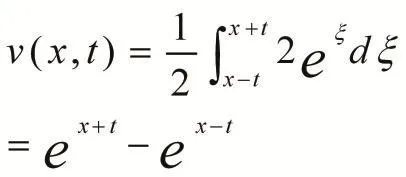
因此原问题的解为：

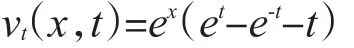
3 结论

本文应用了特解法在受迫振动中的应用，其基本思想是观察泛定方程的类型，寻找合适的特解，再运用叠加原理分解成自由振动方程，进而快速求解。这种方法快速容易掌握，是一种好的方法。

[1]梁昆淼.数学物理方法[M].4版，北京：高等教育出版社，2010．

[2]戴嘉尊，张鲁明.数学物理方程[M].2版.南京：东南大学出版社，2014．

[3]上海交通大学数学系.数学物理方法试题分析与解答[M].上海：上海交通大学出版社，2013.

The Special Solution of Infinite String of Forced Vibration Equation

XU Xiang
(Institute of Theoretical Physics,China West Normal University,Nanchong,Sichuan 637009 China)

A one-dimensional wave equation with unbounded,when not considering the external force,can be directly solved by D'Alembert formula,When considering the external force,D'Alembert formula can not be used directly,but it can be solved by the superposition principle,and then solved.the special solution of the infinite string of forced vibration equation is transformed into the free vibration equation of infinite string,and then by the Darren Bell formula,fast results.

wave equation;Poisson formula;D'Alembert formula

O175.24;O323

A

1673-1891（2016）01-0021-02

10.16104/j.issn.1673-1891.2016.01.006

2015-10-28

西华师范大学科研启动基金（08B057）。

许湘（1981—），男，四川泸州人，讲师，研究方向：理论物理与固体力学。