改进正则项的图像盲恢复方法

贾彤彤,张晓乐,石玉英

(华北电力大学数理学院，北京102206)



改进正则项的图像盲恢复方法

贾彤彤,张晓乐,石玉英

(华北电力大学数理学院，北京102206)

摘要：图像恢复是一个反卷积过程，这一过程通常是病态的，其中的盲恢复是一个最常见也最具挑战性的问题。由于盲恢复过程中缺乏点扩散函数的相关先验信息，使得这个过程变得更为复杂。为了保证在得到光滑图像的同时也可以很好地保持图像的边缘信息，本文提出了一个改进的全变分正则项的盲恢复模型，并结合分裂Bregman算法对模型进行了求解。数值计算中采用了快速傅里叶变换和shrinkage公式来降低计算复杂度。数值实验分别对模糊图、含有噪声和高斯模糊的灰度图进行了处理，得到了满意的结果。

关键词：盲恢复；点扩散函数； 分裂Bregman算法；快速傅里叶变换

1引言

通常情况下，在获取、传输、显示图像的过程中，许多因素会导致图像质量的下降，造成图像的模糊或是含有噪音。图像恢复的目的就是从退化图像的相关信息中得到尽可能接近原始图像的数据，从而恢复图像的本来面目，它在科学的各个领域都发挥着非常重要的作用[1-3]。

在图像处理中，原始图像与观测图像之间的关系可以表达如下：

g=Au+n，

这里g代表退化图像，n是噪声。A是模糊算子(也称为点扩散函数(PSF))，且A=h*u，h是紧凑的卷积核(如：高斯卷积核)，*表示卷积。

一般来说，由于模糊的过程很难得到，这使得PSF很难确定。因此我们只能在缺乏PSF的先验信息的情况下，从观测到的图像g中提取一些有用的信息来得到恢复图像u，这一过程就称为图像盲恢复。它的优点是在没有任何图像退化的先验知识的情况下也可以实现图像恢复过程。

反卷积过程中的病态特性，是反问题本身固有的一种特征。病态问题在图像处理中意味着即使真实图像中存在某些微小扰动，也可能造成逆变换中不可忽视的影响，严重影响研究的准确性。通常在解决病态问题时，并不要求获得该问题的精确解，而是寻求具有物理意义的近似解，并且希望该近似解从计算角度而言是充分稳定的。

解决病态性最一般的方法就是在目标函数的基础上添加正则项，从而保证解在物理意义上是合理的，并且连续地依赖于数据。You等[4]考虑在目标函数的基础上对于图像和模糊核都添加H1正则项，然而，由于H1项的各向同性性质却不能很好地保持边缘信息。之后，Chan等[5]提出利用全变分正则项‖▽u‖1和‖h‖1来代替H1项并得到一个最小化模型。2012年，Li等[6]应用文献[7]中的方法解决了下面的盲恢复问题：

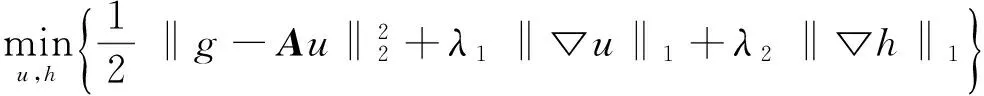
(1)

其中，λ1>0，λ2>0。

基于全变分(TV)正则项的图像去噪方法已经有了很多的研究。Rudin，等[8]提出的Rudin-Osher-Fatemi(ROF)模型是图像恢复中的一个非常经典的模型。ROF模型最重要的一个性质就是可以很好地保持图像的边缘信息，但由于‖▽u‖1项，可能会产生“阶梯效应”。为了弥补这一缺陷，2013年，Cai等[9]在Muford-Shah模型[10]的基础上提出了如下模型解决了非凸问题所带来的复杂性：

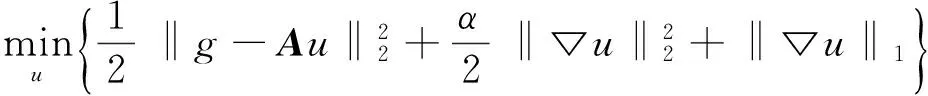
(2)

其中，α>0是平衡保真项与TV项的参数。

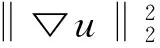
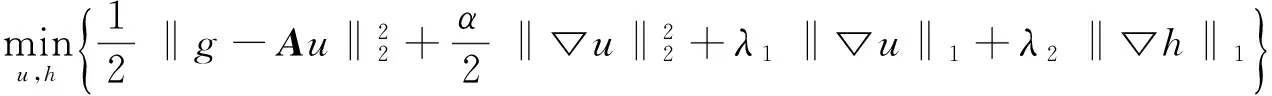
(3)

如此一来，模型(3)可以保证在得到清晰的恢复图像的同时也可以很好地保持图像的边缘信息。

由于TV函数的非线性及不可导性，所以很难计算。随着学者们多年的研究，已经有很多方法可以解决这类问题，例如不动点迭代[3,11]、对偶方法[2]、梯度下降法[12]、交替迭代法[13]和分裂Bregman算法[7]等。由于分裂Bregman迭代具有显著的稳定性和快速的收敛性，因此被广泛地应用于图像恢复中。本文，我们的模型(3)同样用分裂Bregman方法来解决。

2图像盲恢复数值实验

一般来说，对于一个特定的目标函数，用Bregman迭代的收敛速度很快，尤其是对于含有L1正则项的优化问题。而分裂Bregman算法可以把优化问题中的L1和L2范数分离开来变成几个子问题的形式，进而便于计算。故这一部分主要应用分裂Bregman方法来解决模型(3)。由于计算过程中的数据较大，因此用到了快速傅里叶变换(FFT)和shrinkage公式来降低算法的复杂度，从而缩短了计算时间。为了解决模型(3)中的两个L1正则项，我们参考文献[4]，引入辅助变量c=(cx,cy)，d=(dx,dy)，并做如下替换：

cx=▽xh，cy=▽yh，dx=▽xu，dy=▽yu，

则我们可以得到与模型(3)等价的约束优化问题：

(4)

s.t.cx=xh,cy=yh,dx=xu,dy=yu。

添加二次罚函数，将上述约束问题转为非约束问题，得到算法的第k+1步为：

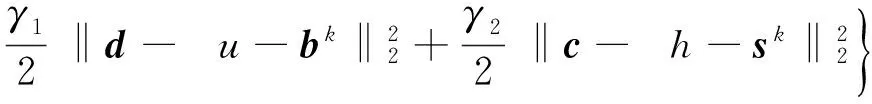
(5)

其中，参数γ1>0，γ2>0，且

bk+1=bk+uk+1-dk+1，

sk+1=sk+hk+1-ck+1。

(6)

问题(5)～(6)的解可以通过一个给定的初始值u0，应用交替迭代技术计算如下序列

h1,u1,h2,u2, …,hk,uk,hk+1,uk+1, …，

然后求解下列4个子问题得到。

(1)h子问题：对于固定的uk, ck, sk，得

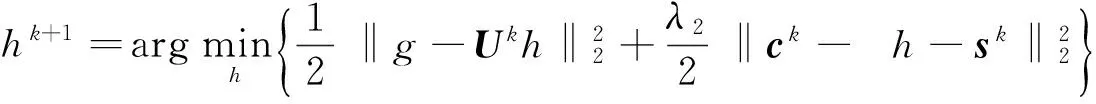
(7)

其中U是由图像u形成的块循环矩阵[6]。

这里以在周期边界条件下为例，介绍块循环矩阵U的形成过程。设u为3×3阶矩阵，即

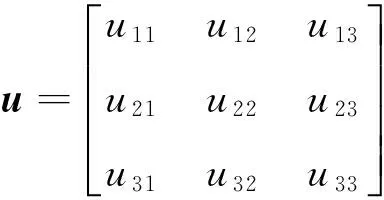
那么通过构造块循环矩阵得到的U为

类似U矩阵的形式就叫做BCCB(block circulant with circulant blocks)矩阵，它可以有效地进行谱分解，加快计算速度。

根据一阶最优化条件，得到(7)的欧拉-拉格朗日方程

[(Uk)TUk-γ2Δ]hk+1=(Uk)Tg+γ2▽T(ck-sk)，

(8)

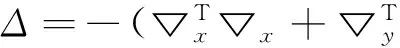
因为我们的算法是在周期性边界条件下进行的，并且U通常是一个很大的循环矩阵，所以可以用快速傅里叶变换[5](FFT)来降低算法的复杂度。即

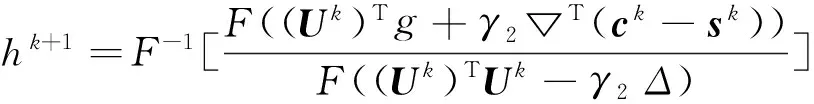
(9)

其中，F表示快速傅里叶变换。

(2)u子问题：对于固定的hk+1, dk, bk，有

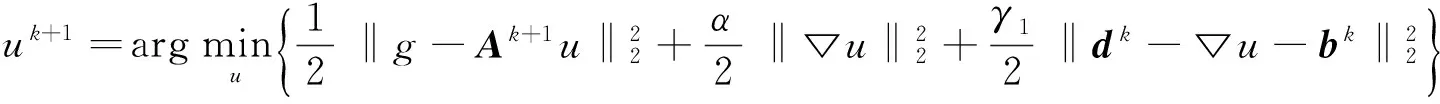
(10)

与h子问题相似，我们需要解决

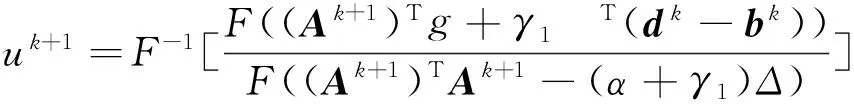
(11)

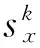
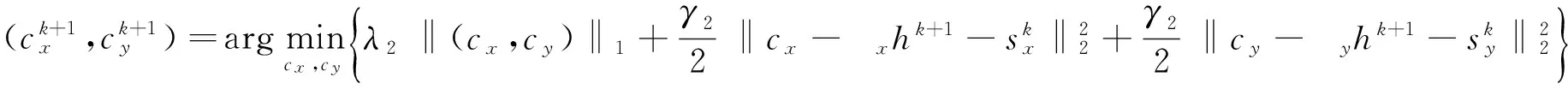
(12)

应用shrinkage公式(见[7])，上述子问题(12)的显式解为

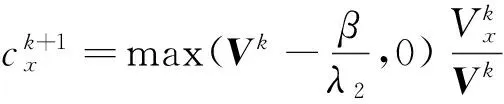
(13)

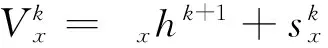
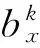
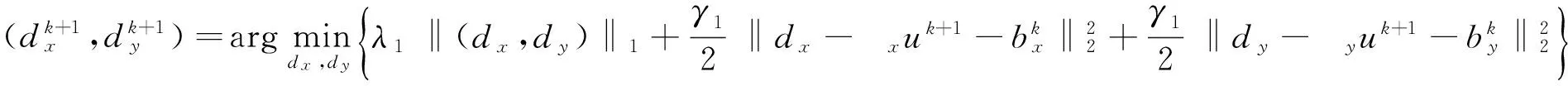
(14)

子问题(14)的显式解为

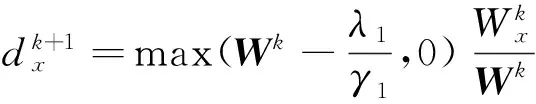
(15)

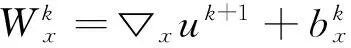
由此，我们可以看出每个子问题都可以通过快速傅里叶变换或显式解进行求解。于是我们得出如下算法：

ⅰ.初始化：令c0=s0=0, d0=b0=0,u0=g。

ⅱ.对于k=0, 1, …, 有

a:由迭代格式(9)得hk+1，

b:由迭代格式(11)得uk+1，

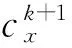
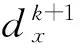
ⅲ.满足终止条件则停止。

因为这个过程始于初始值u0，所以h子问题和u子问题的位置不能改变。

之所以说分裂Bregman算法具有较快的收敛速度及较好的稳定性[7]，第一是由于一般来说γ越大，则对模型的约束作用越大，对噪声的抑制作用越强，而分裂Bregman算法对数值很大的γ也能够适应。第二是由于算法的计算速度是依赖于算法中使用的Bregman迭代。考虑一个更特殊的形式，如果令λ2→∞，添加的二次罚函数会起到很大的作用，其中任意一个微小的变量都将对计算结果起到不可忽视的作用，(8)式就变为一个具有病态性的问题，这时使用普通的算法(如高斯-赛德尔方法)将会失效，但分裂Bregman方法仍然适用。因此说分裂Bregman方法具有较好的稳定性。

3数值实验

为了使得结果更令人信服，本节分别对模糊图像、含有噪声和模糊的图像进行了处理，并将模型(3)与模型(1)的恢复效果进行了比较。

下述所有实验中，设误差Δ为内循环迭代停止条件。当Δ<10-4时，外循环达到50次时，计算迭代停止。误差Δ定义如下：

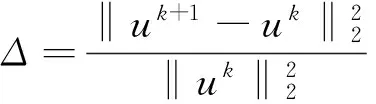
度量恢复后的图像是否为最接近原始图像的状态有许多种方法。既可以从主观上通过视觉来进行观察，也可以从客观上用一定的评价指标来度量，如信噪比、相似度和平均绝对误差增益等。但最好的方式是客观评价与主观评价达到一致，且容易计算。

本文采用的客观评价为改善信噪比，其计算公式为[14]：

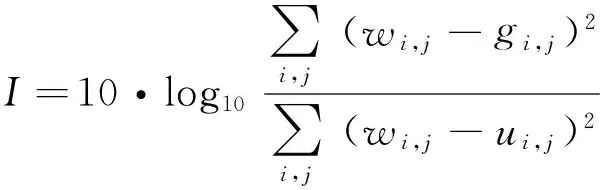
式中，I为改善信噪比(ISNR)；wi,j,gi,j,ui,j分别表示原始图像、观测图像和复原图像的像素值。一般来说，改善信噪比的值越大，恢复图像就越接近于原图像。

本文所有实验均添加两种模糊，分别是像素尺寸为10×10，方差σ2=1的高斯模糊(GB)，和像素尺寸为10×10，方差σ2=1的Moffat模糊(MB)，并对图1中的两幅原始图像进行了处理。

图1　原始图像Fig.1　The original image

3.1模糊图像的复原

对于高斯模糊，模型(1)与模型(3)选取相同的参数λ1=1×10-5,λ2=1×10-2,γ1=1×10-4,γ2=70，另外在模型(3)中选取α=1×10-5。对于Moffat模糊，选取相同的参数λ1=1×10-5,λ2=0.2,γ1=2×10-4,γ2=60，模型(3)中选取α=5×10-8。

图2的第一列给出了退化图像，第二列给出了应用模型(1)的恢复图像及其改善信噪比值，第三列给出了应用模型(3)的恢复图像及其改善信噪比值。

图2的结果表明两个模型都可以得到较满意的恢复图像。尽管从视觉上看模型(3)比模型(1)的优越之处不是很明显，但从改进信噪比的值的大小来看，模型(3)能够得到比模型(1)较大的改善信噪比值。说明相对模型(1)，模型(3)是一个改进。

3.2含有模糊和噪音的图像复原

在电力系统应用中，由于图像采集设备本身的缺陷和周围环境的影响，采集到的图像中难免会含有模糊和噪声，这对设备的检测、识别和研究等都带来严重的影响，并且会降低处理结果的正确性。因此，对采集到的电力设备图片进行预处理，尽可能恢复图片原始的状态是很有必要的。[15]

我们对绝缘子图片分别添加与上节相同的两种模糊，并在此基础上添加噪声强度为1%的高斯噪音。这里的两种模糊参数均设定为λ1=1×10-5, λ2=0.2, γ1=2×10-4, γ2=60，且在模型(3)中选取α=5×10-5。图3给出了绝缘子图片分别用两种模型得到的恢复结果。从图中的结果我们可以看出，经过模型(1)和模型(3)的处理后，绝缘子柱子上的螺纹可以更清晰地显现出来，且图像最底端的字母也可以看得更清楚了。比较两个模型的恢复后的改善信噪比，模型(3)可得到比模型(1)更大的改善信噪比值，恢复效果更好。

图3　含有模糊和高斯噪音图像的复原结果Fig.3　Restoration of blurry and Gaussian noise contaminated image

4结语

本文我们首先介绍了图像反卷积的病态性，并引出了基于ROF模型的改进正则项的盲恢复模型。接着运用具有较快收敛速度和较好稳定性的分裂Bregman算法对模型进行了求解，并且运用FFT和shrinkage公式加快了计算速度。最后，仿真实验分别对不同类型的模糊图像，含有噪音和模糊的绝缘子图像进行了测试，并用改进信噪比对恢复结果进行了客观评价。又通过与模型(1)的比较，证实了模型(3)比模型(1)更优越。综上所述，我们所提出的模型能够在PSF缺乏先验知识的前提下得到很好的恢复图像。

参考文献：

[1]LIU J J, SHI Y Y, ZHU Y G. A fast and robust algorithm for image restoration with periodic boundary conditions [J].Journal of Computational Analysis and Applications, 2014, 17(3): 524-538.

[2]CHAN T F, GOLUB G H, MULET P. A nonlinear primal-dual method for total variation-based image restoration [J].SIAM journal on scientific computing, 1999, 20(6): 1964-1977.

[3]SHI Y Y, CHANG Q S. Efficient algorithm for isotropic and anisotropic total variation deblurring and denoising [J].Journal of Applied Mathematics, 2013, 2013,Aticle ID 797239.

[4]YOU Y L, KAVEH M. A regularization approach to joint blur identification and image restoration [J].Image Processing, IEEE Transactions on, 1996, 5(3): 416-428.

[5]CHAN T F, WONG C K. Total variation blind deconvolution [J].Image Processing, IEEE Transactions on, 1998, 7(3): 370-375.

[6]LI W H,Li Q L, GONG W G,et al.Total variation blind deconvolution employing split Bregman iteration [J].Journal of Visual Communication and Image Representation, 2012, 23(3): 409-417.

[7]GOLDSTEIN T, OSHER S. The split Bregman method for L1-regularized problems[J].SIAM Journal on Imaging Sciences, 2009, 2(2): 323-343.

[8]RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms[J].Physica D: Nonlinear Phenomena, 1992, 60(1): 259-268.

[9]CAI X H,CHAN R, ZENG T Y. A two-stage image segmentation method using a convex variant of the Mumford-Shah model and thresholding[J].SIAM Journal on Imaging Sciences, 2013, 6(1): 368-390.

[10]MUMFORD，SHAH D. Optimal approximations by piecewise smooth functions and associated variational problems[J].Communications on Pure and Applied Mathematics,1989,42(05):577-685.

[11]MARQUINA A, OSHER S. Explicit algorithms for a new time dependent model based on level set motion for nonlinear deblurring and noise removal[J].SIAM Journal on Scientific Computing, 2000, 22(2): 387-405.

[12]HE L, MARQUINA A, OSHER S. Blind deconvolution using TV regularization andBregman iteration[J].International Journal of Imaging Systems and Technology, 2005, 5:74-83.

[13]WAND Y L, YANG J F, YIN W T,et al.A new alternating minimization algorithm for total variation image reconstruction [J].SIAM Journal on Imaging Sciences, 2008, 1(3): 248-272.

[14]刘晶晶．基于Split Bregman方法的图像盲恢复研究[D].北京：华北电力大学，2013.

[15]方金.基于偏微分方程的电力设备红外图像增强和分割方法研究[D].吉林：东北电力大学，2014.

DOI:10.3976/j.issn.1002-4026.2016.03.020

收稿日期：2015-12-24

基金项目：国家自然科学基金(11271126)；中央高校基本科研业务费专项资金资助(2014ZZD10)

作者简介：贾彤彤(1990-)，女，硕士研究生，研究方向为图像处理。Email:jttncepu@163.com

中图分类号：TP391

文献标识码：A

文章编号：1002-4026(2016)03-0115-08

Image blind deconvolution approach with modified regularization term

JIA Tong-tong, ZHANG Xiao-le, SHI Yu-ying

(Department of Mathematics and Physics, North China Electric Power University, Beijing 102206, China)

Abstract∶Image restoration is a deconvolution process, which is usually morbid. Blind deconvolution is one of the most common and challenging problems. Without priori knowledge on point spread function, the process is therefore more complex. To preserve the edge information of an image as well as its smoothness, we present a blind deconvolution model with a modified total variation regularization term. We also solve the model with split Bregman iteration algorithm. Fast Fourier transform and shrinkage formula are applied in numerical calculation to reduce its computational complexity. We apply the model to the processing for a blurry image and a greyscale image with noise and Gaussian blur in numerical experiment, and then obtain satisfactory results.

Key words∶ blind deconvolution; point spread function; split Bregman algorithm; fast Fourier transform