航班计划的优化设计研究
2016-08-01程望斌冯彩英罗百通向灿群湖南理工学院信息与通信工程学院湖南岳阳414006
程望斌,冯彩英,曾 毅,罗百通,向灿群(湖南理工学院 信息与通信工程学院,湖南 岳阳 414006)
航班计划的优化设计研究
程望斌,冯彩英,曾 毅,罗百通,向灿群
(湖南理工学院 信息与通信工程学院,湖南 岳阳 414006)
以航空公司的正常营运和最大收益为目标,结合统计数据和目标要求,建立航班计划动态规划模型,采用贪婪算法对其进行求解,得到航空公司的航班计划、飞机数量的规划,从而为航空公司编制和优化航班计划提供一定的理论依据和方法支持. 以某航空公司特定机型的航班计划数据进行实证,验证了该模型和算法的可行性.
航班计划; 动态规划; 贪婪算法; 优化设计
引言
航班计划(Schedule)是航空公司一切生产活动的基础和核心,其它任何生产计划都是围绕航班计划来制定,并为航班计划的顺利实施提供保障[1]. 航班计划是航空公司运输生产计划的具体实施计划,它规定了飞行的航线、航段、机型、航班号、班次和班期、起降时刻等. 航空公司运行指挥中心每个月的月末都会对本月各航线、机型的收益情况进行市场分析,然后结合本公司现有的生产资源情况编排下一个月的航班计划,在航班计划制定之后需送给机务部门进行飞机排班作业,机务部门在制定飞机排班计划时主要考虑满足飞机维修的需要,飞机排班计划完成以后形成可执行的航班计划,该计划需下发到飞行总队具体执飞. 一个合理的航班计划应该既有助于航班的安全运行,又能提高飞机的利用率,还可以有效地降低运营及维护成本,提高公司的经济效益[2]. 本文将某航空公司根据市场要求安排的航班时刻汇总的所有可以选择的候选航班,作为优化决策的备选方案. 航班计划时刻优化决策即从候选航班中选择最佳方案,使飞机数目最少,航空公司利益最大化.
1 问题提出与分析
国内某个以客运为主的航空公司运行指挥中心每个月的月末都会对本月各航线、机型的收益情况进行市场分析,然后结合本公司现有的生产资源情况编排下一个月的航班计划,在航班计划制定之后需送给机务部门进行飞机排班作业,机务部门在制定飞机排班计划时主要考虑满足飞机维修的需要,飞机排班计划完成以后形成可执行的航班计划,该计划需下发到飞行总队具体执飞.
已知该公司有两种类型的飞机,A320飞机和E190飞机. 其中A320飞机2架,E190飞机4架. 维修基地设在西安和天津. 由于航线资源是航空公司的稀缺资源,所以制定航班计划时一般不会取消,也不会随意拆分带有经停航点的航线. 在航班计划制定时,若本公司飞机数量无法满足现有航线需要,可向专业的飞机租赁公司申请租赁; 反之,若在满足现有航线需要的前提下,本公司尚有一定数量的剩余飞机,则可作为备用飞机在航线发生延误及飞机出现临时故障时使用,或者直接出租给其它航空公司以便获取额外利润. 已知该公司某月各航线单日运行成本及收入明细,并假定每个航线每日只安排一个班次的飞机,各航线的航班时刻可以根据需要变动,同时假定现有飞行航线和航空公司的营销能力是稳定的. 为此航空公司需制定一份下个月的航班计划,使航空公司的收益最大化.
2 飞机排班计划的数学模型建立
飞机排班是航班计划的一项控制性工作,排班质量不仅决定着运输生产能否安全、正点的运行,而且还关系到飞机维护计划能否顺利执行[3]. 飞机排班工作中必须遵守以下基本要求: 飞机排班应与制定的航班计划相符; 每条航线应当且仅安排一架飞机执行任务; 每架飞机在同一时段最多只能执行一条航线的任务; 飞机的使用要求均衡; 在航班计划正常营运的情况下,所需飞机数目最少,使航空公司获取最大化的收益.
要满足上述要求,关键是做到: (1)根据紧凑衔接的原则将航班节编组,然后对航班节组指派飞机; (2)允许对标准过站时间GT进行压缩,但不得低于最低过站时间即GTmin; (3)重要航班应优先保障; (4)应尽量减少由于过站时间压缩而引起的航班延误. 为此建立如下飞机排班数学模型:
航班节集合定义为J={Ji,j=1,…,n },n表示航班节总数,所有可用于执行航班任务的飞机集合为F=|k=1,…,m},m表示某机型的飞机数量,机场的集合定义为D={Di |i=1,2,…,d },d表示所有可到达的机场总数,某飞机的起点与前一个航班任务的降落点为同一地点的匹配函数为

式(1)中,在枢纽机场的起飞时间为rt,在枢纽机场的过站时间为GT,某飞机在航班节中包含的起降次数为jC,飞行时间为jt,完备时间为jtf,航班节的时间要求jta,飞行成本为C,飞机收入为L,飞机与航班节的匹配函数定义
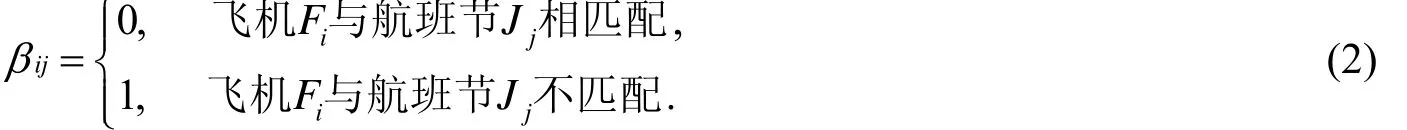
飞机任务是否执行定义为

完成所有的航班任务所用的飞机数量为


根据排班原则“飞机型号与所分配的航班节相匹配”,即

根据排班原则“同一架飞机的相邻两个航班应符合过站时间衔接”,即

根据排班原则“同一架飞机的相邻两个航班应符合航班地点衔接”,即

根据排班原则“一架飞机的总的飞行时间与过站时间之和不大于标准工作间”,
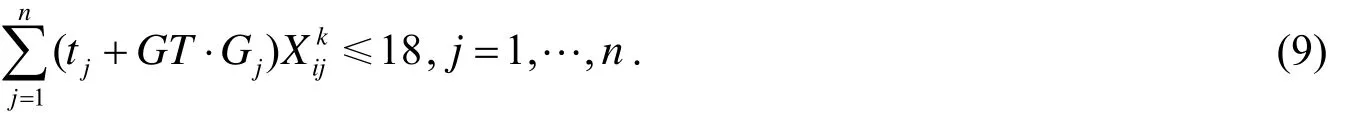
根据飞机排班原则“一架飞机执行的飞行任务必须满足航班节的时间要求”,

根据排班原则“所有航班节有且只有一架飞机执行”,因此,对于任意航班节i,有且只有一个是否执行任务的变量Xikj为“值1”,即

根据排班原则“一架飞机同一时间段最多只能执行一个航班节任务”,因此飞机k在执行完航班节i之后,最多只能执行一个后续航班节j,即对于给定的飞机k与航班节i,飞机任务是否执行变量最多只有一个为“值1”,即

同理飞机k在执行航班节j之前,最多只能执行一个航班节i,即对于给定的飞机k与航班节j,飞机任务是否执行变量Xikj最多只有一个为“值1”,即:

根据排班原则“全部飞行任务执行完毕后,双枢纽机场的飞机数量与执行任务飞机数量一致”即
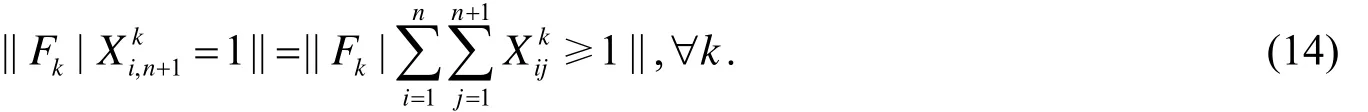
综合(5)~(14)即可得到飞机对航班节分配问题的数学模型:
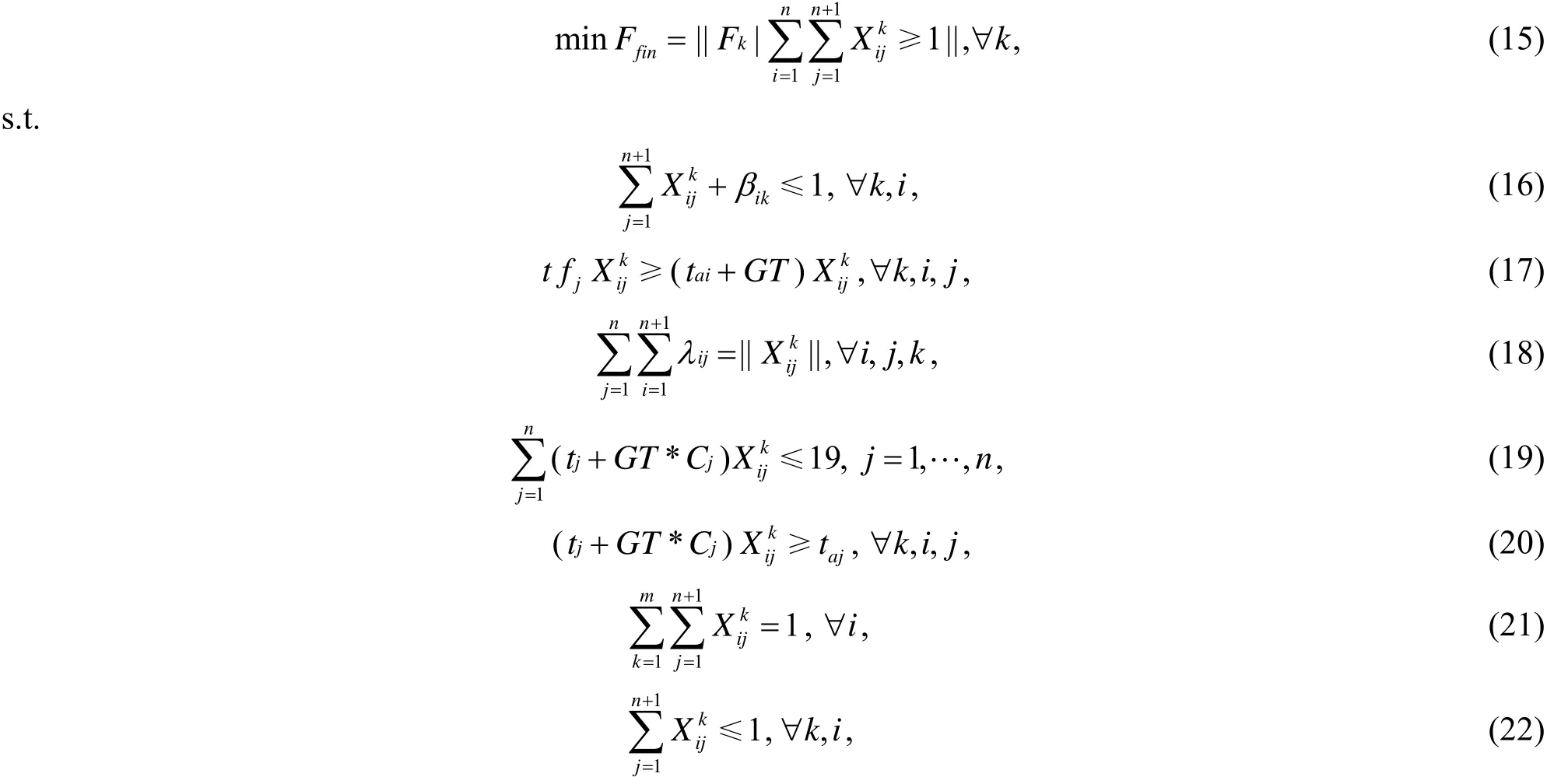
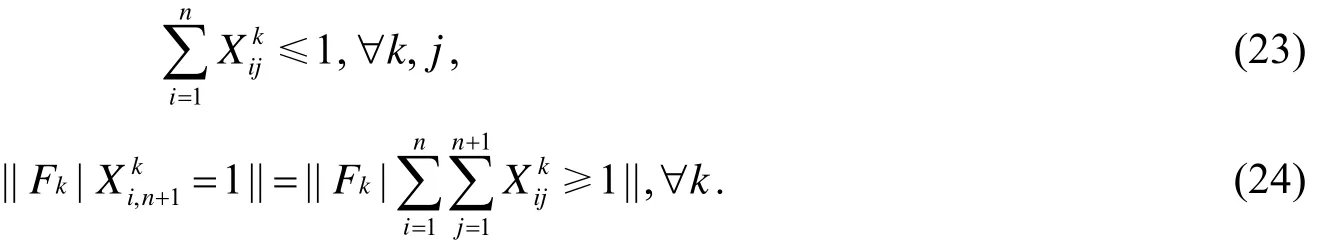
其中公式(15)为目标函数,公式(16)至公式(24)为约束条件[4].
3 航班计划的编排
航空公司在制定计划时的一项基本内容就是飞机排班,飞机排班是指: 飞机调度员根据市场部下达的航班计划,机务部提供的飞机维修计划,每架飞机的技术状况以及飞机调度指令,为每个航班指定一架具体执行的飞机.
3.1 飞机排班的算法设计
我们建立的飞机排班的数学模型是一个动态规划问题[5],且含有多个约束条件. 目前解决该类问题的算法有很多,如随机模拟算法,遗传算法等. 由于文中涉及的机型仅为两种,航班节仅有26个,因此可考虑用遍历的方法寻找最优解. 同时,本文还使用贪婪算法[6]对问题进行了求解,并在此基础上进行算法的改进,使其尽可能的满足飞机使用均衡.
(1) 扫描法寻找最优解
扫描的基本思想就在于能够遍历所有解,记录产生的最优解,直到有新的最优解替代它. 算法基本流程如下:
Step1 递归实现二路归并排序实现所有解的遍历;
Step2 比较每一个解下面目标函数值与所设最小值,如果小于所设最小值则完成最小值的替代,并记录此解;
Step3 遍历以后输出最小值和此最小值下的解.
用此算法得到过站时间设为20~50min,每个枢纽点需要的不同飞机最小数量见表1.
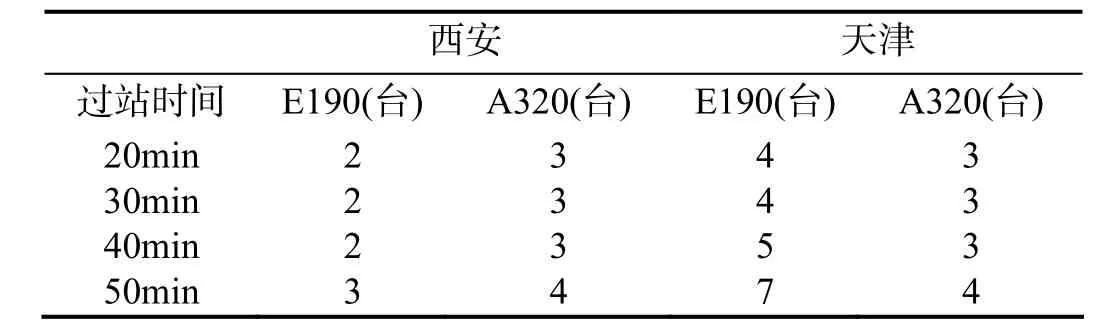
表1 飞机排班情况
(2) 贪婪算法寻找最优解
贪婪算法是指在对问题求解时,总是做出在当前看来是最好的选择. 也就是说,不从整体最优上加以考虑,它所做出的是在某种意义上的局部最优解,但它可以大大提高运算速度,加快收敛,应用于更大数量的航班节指派飞机场合.
针对我们所建立的飞机排班模型,具体均衡贪婪算法的实现如下:
Step1 对所有航班节以其完成的时间长短进行从大到小的排序;
Step2 将航班节绑定在可以绑定的飞机上,如有多台飞机可完成绑定,则优先绑定目前工作时间短的飞机,并标识;
Step3 如果没有可绑定的飞机,则指派一架新的飞机来绑定该航班节,并标识;
Step4 完成所有航班节的绑定,并将结果输出.
通过实验得到的均衡贪婪算法实验结果和扫描法结果一致,验证了该算法的可行性.
3.2 航班计划的实现
采用均衡贪婪算法可以得到飞机排班指派表如表2所示.
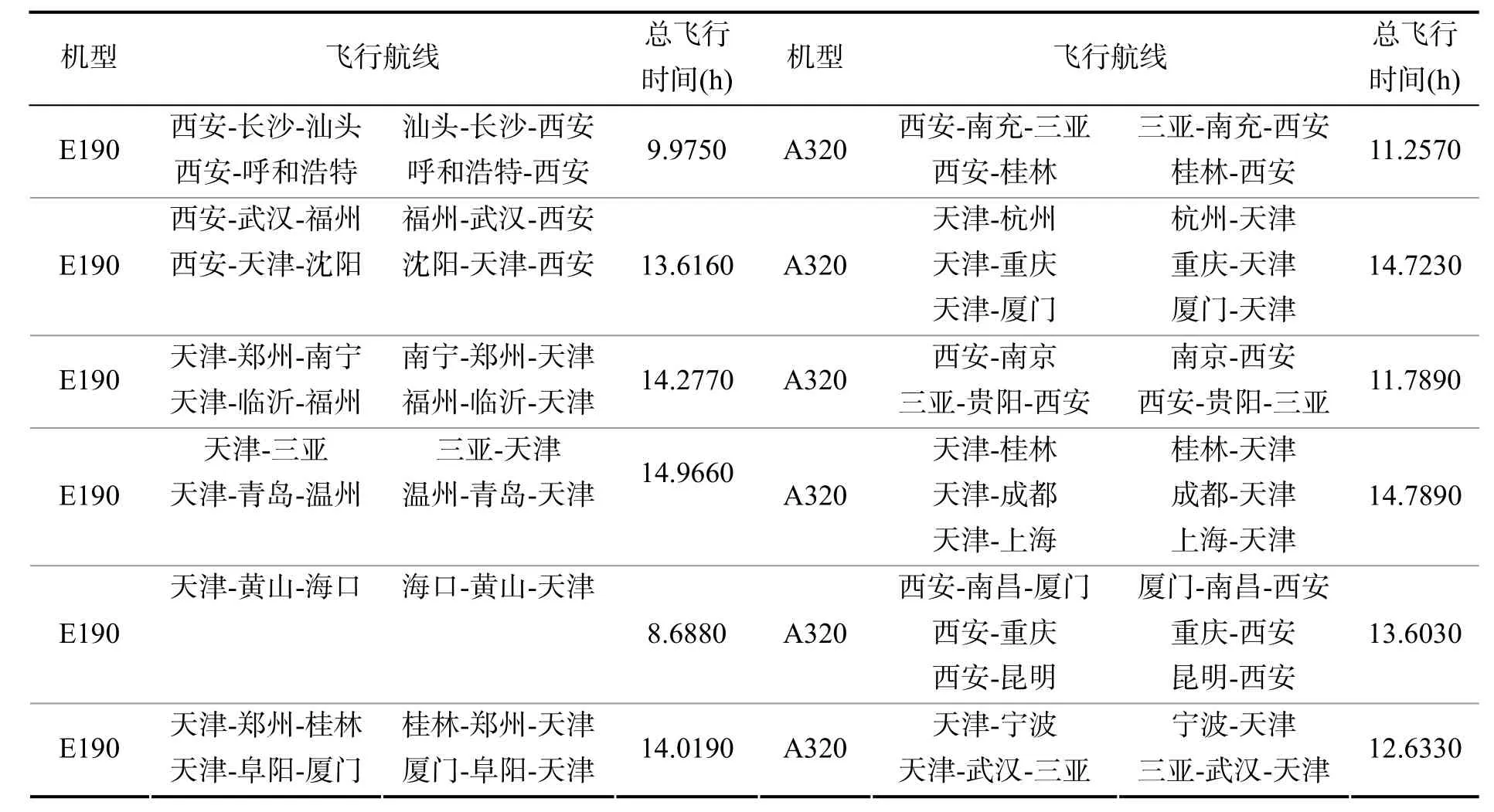
表2 飞机执行表(A320机型过站时间为40min,E190过站时间30min)
同时本文还对A320过站时间为30min进行了仿真,得到的结果和过站时间为40min一样,而A320过站时间为50min则需要增加飞机数量,因此设置A320过站时间为40min. 同时也对E190过站时间分别为40min、50min进行了仿真,得到过站时间为40min时E190需要增加一架飞机,50 min则需要更多,因此设置E190过站时间为30 min,可以达到效益最大化.
根据算法给出的航班串组成及各航线往返耗时能给出航班的具体排班及起降时间表. 各航班的起飞时间确定主要考虑如下四个因素:
(1) 最早航班的起飞时间和最晚航班的降落时间在合理范围;
(2) 只有一个航班的航班串,起飞时间尽量和给出的数据相吻合;
(3) 航班串中有多个组成时,先后顺序的确定也尽量保持一致,在无法都保证的情况下优先考虑收益多的航班;
(4) 起飞时间和降落时间错开,尽量避免同一基地机场存在多架飞机同时起飞或同时降落的情况.
各航班排班结果如表3所示.
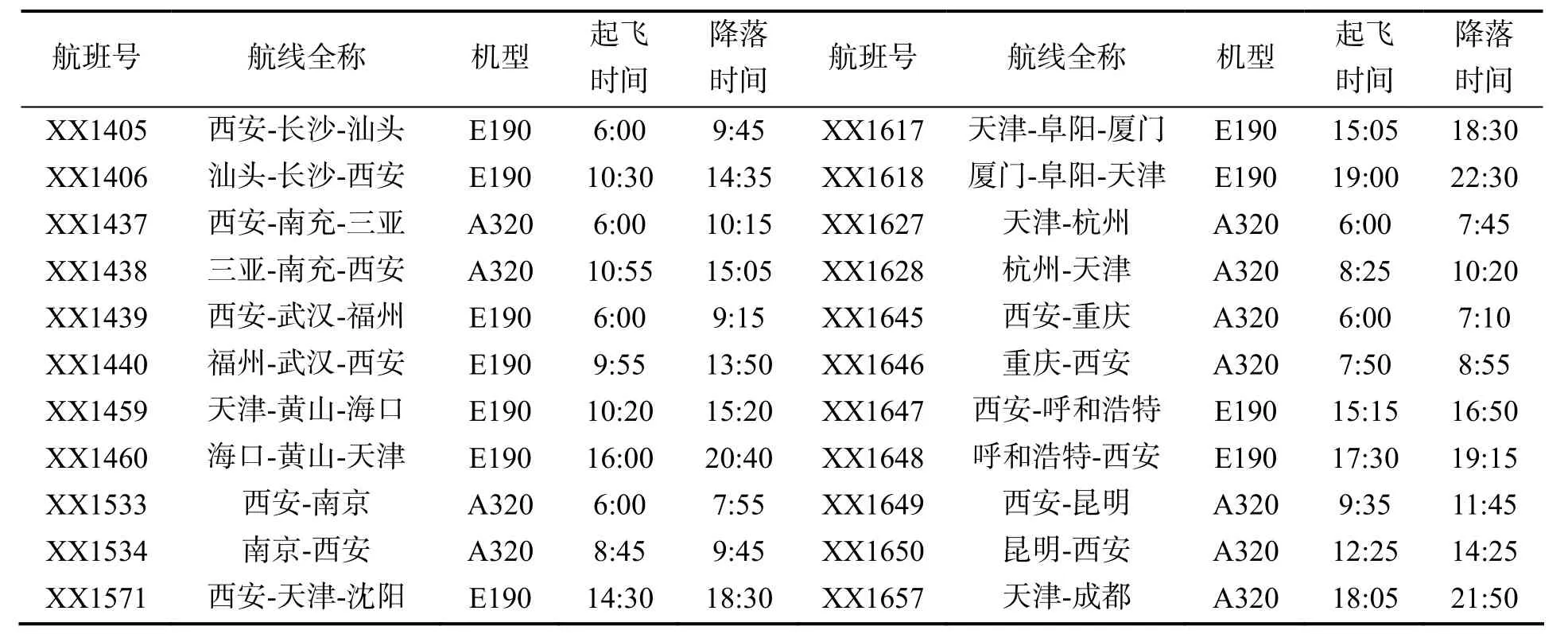
表3 各航班排班结果
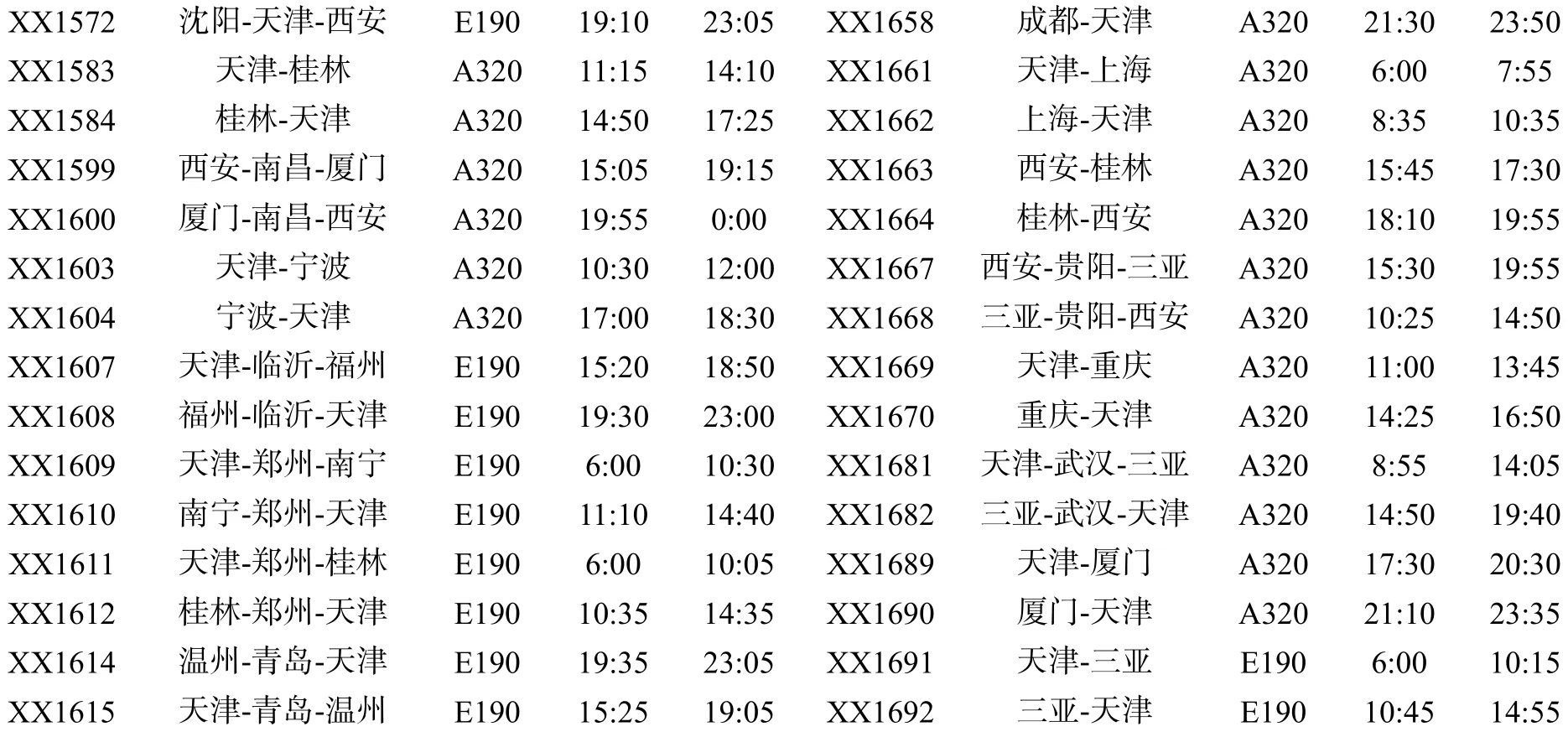
XX1572 E190 19:1023:05XX1658成都-天津 A320 21:30 23:50 XX1583 天津-桂林 A320 11:1514:10XX1661天津-上海 A320 6:00 7:55 XX1584 桂林-天津 A320 14:5017:25XX1662上海-天津 A320 8:35 10:35 XX1599 西安-南昌-厦门 A320 15:0519:15XX1663西安-桂林 A320 15:45 17:30 XX1600 厦门-南昌-西安 A320 19:550:00 XX1664桂林-西安 A320 18:10 19:55 XX1603 天津-宁波 A320 10:3012:00XX1667西安-贵阳-三亚A320 15:30 19:55 XX1604 宁波-天津 A320 17:0018:30XX1668三亚-贵阳-西安A320 10:25 14:50 XX1607 天津-临沂-福州 E190 15:2018:50XX1669天津-重庆 A320 11:00 13:45 XX1608 福州-临沂-天津 E190 19:3023:00XX1670重庆-天津 A320 14:25 16:50 XX1609 天津-郑州-南宁 E190 6:00 10:30XX1681天津-武汉-三亚A320 8:55 14:05 XX1610 南宁-郑州-天津 E190 11:1014:40XX1682三亚-武汉-天津A320 14:50 19:40 XX1611 天津-郑州-桂林 E190 6:00 10:05XX1689天津-厦门 A320 17:30 20:30 XX1612 桂林-郑州-天津 E190 10:3514:35XX1690厦门-天津 A320 21:10 23:35 XX1614 温州-青岛-天津 E190 19:3523:05XX1691天津-三亚 E190 6:00 10:15 XX1615 天津-青岛-温州 E190 15:2519:05XX1692三亚-天津 E190 10:45 14:55
由表3可知,飞机降落时间均未超过凌晨一点,符合机场实际情况. 同一基地中所有航班的起飞和降落时间均不同,很好地错开了时间,避免了机场拥塞,满足了以上四个主要因素的要求,所以表3的排班接近最优且实际可行.
4 结语
本文设计的航班计划,虽然是在固定模式下制定的,有一定的局限性,但其中建立的模型和采用的分析方法对我国航班计划的制定具有一定的借鉴作用. 由于时间和知识水平的关系,还有不少因素需要考虑,有不少环节需要优化设计,因此模型的设计和航班计划的优化还有待进一步完善[7].
[1]张海峰,胡明华. 航空公司短期航班计划编排模型及算法[J[. 南京航空航天大学学报,2015,47(4): 553~558
[2]罗 俊,阎 煜. 短期航班调整的利润分析[J[. 知识经济,2012(6):138~139
[3]刘 山,秦易达.飞机排班模型的分层优化方法[J[. 计算机仿真,2014,31(2): 111~115
[4]谭 娜,李耀华. 基于改进遗传算法的机组指派优化方法研究[J[. 控制工程,2015,22(4): 674~678
[5]张伯生,刘 飞. 实现航班计划优化的动态规划模型[J[. 上海工程技术大学学报,2004,18(2): 135~141
[6]晏 杰. 基于改进的贪婪算法在0/1背包问题中的研究与应用[J[. 廊坊师范学院学报(自然科学版),2011,11(5): 27-30
[7]高 伟,张腾飞. 随机模拟法在仿真航班计划生成中的应用[J[. 科技创新导报,2014,(2): 89~91
Research on Optimization Design of Flight Plan
CHENG Wang-bin,FENG Cai-ying,ZENG Yi,LUO Bai-tong,XIANG Can-qun
(College of Information and Communication Engineering,Hunan Institute of Science and Technology,Hunan Yueyang 414006)
Taking normal operation of the airline and the maximum profit as the goal,combining with the statistical data and the goals and objectives,flight schedule dynamic programming model was established. The greedy algorithm was used to plane the airline's flight plan and the number of aircraft. So as to provide theoretical basis and method support for airline coding system and the optimization of flight plan. The feasibility of the model and algorithm was verified by the data of flight plan of a certain airline.
flight planning,dynamic programming,greedy algorithm,optimization design
F560
A
1672-5298(2016)02-0038-05
2016-03-18
程望斌(1979- ),男,湖北咸宁人,硕士,湖南理工学院信息与通信工程学院副教授. 主要研究方向: 光电子技术、学科竞赛
