深基坑双排桩结构受力变形机理及其计算模型研究

薛光桥

(1.中铁第四勘察设计院集团有限公司，武汉　430063；2.水下隧道技术湖北省工程实验室，武汉　430063)



深基坑双排桩结构受力变形机理及其计算模型研究

薛光桥1，2

(1.中铁第四勘察设计院集团有限公司，武汉430063；2.水下隧道技术湖北省工程实验室，武汉430063)

摘要：近年来，为了适应国内城市地下工程建设蓬勃发展带来的地下工程密集化、复杂化等方面的需要，深基坑开挖时双排桩围护结构因具有侧向刚度大、控制变形能力强、施工快速等特点在各种大型深基坑工程中得到了较为广泛的推广和应用。但实际设计过程中，由于该结构的变形机理与计算模型尚未有统一的理论，其设计方法比较杂乱，存在一定程度的保守设计。依托南京梅子洲青奥城地下空间工程及其现场监测数据，采用有限元计算模型对近年来在地下工程中逐渐得到推广使用的双排桩围护结构的变形机理、土压力分布规律等进行探讨和研究；在此基础上，结合与目前广为应用的理正双排桩模型和新规范双排桩模型的对比分析，研究并提出更吻合实际的、精确反映结构变形和力学特性的双排桩围护结构的修正设计计算模型，该模型架构清晰，准确性高，贴近实际工程设计，可以大力推广应用于双排桩结构的计算分析。

关键词：深基坑，双排桩，变形机理，计算模型，有限元法

1概述

近年来，为了适应国内城市地下工程建设蓬勃发展带来的地下工程密集化、复杂化等方面的需要，深基坑开挖时双排桩围护结构因具有侧向刚度大、控制变形能力强、施工快速等特点在各种大型深基坑工程中得到了较为广泛的推广和应用[1-2]。

国内从20世纪90年代初即开始对双排桩围护结构进行了初步的探索，随后大量的研究人员结合模型试验、工程实测理论推导等对双排桩结构的设计理论、土压力分配方法、计算模型、工程应用等进行了研究，例如，张弘、林栋[3-4]等人考虑连梁与前、后排桩的铰接情况，近似地将桩间土体视为受侧向约束的无限长弹性土体，且横向应变为零，应用经验系数调整前、后排桩所受的侧向土压力；何颐华[5]根据双排桩前、后排桩之间的滑动土体占桩后滑动土体总量的体积比例来确定前、后排桩所受侧向压力；熊巨华[6]首次在文献中提出对于前、后排距小于4倍桩径的双排桩支护结构，给出等效抗弯刚度的计算方法；郑刚[7]等人提出将双排桩之间的土视为薄压缩层，并以水平向弹簧模拟，可以考虑两排桩之间的土层分布变化、压缩性、桩间土加固等对双排桩相互作用的影响，避免对前、后排桩土压力做出人为的分配。此外，还有弹性地基梁模型[8]、破裂面假设模型[9-10]和土拱理论模型[11-12]等。

上述研究成果对双排桩围护结构的理论完善和工程应用起到了较大的促进作用，但是这些现有的不同计算模型和方法即使在相同计算参数的情形下，对同一工程项目得到的计算结果仍有较大的差异，不同的计算模型对双排桩结构的变形和受力机理也存在诸多的解释，给工程设计和工程建设带来了诸多困惑与困难。

以南京梅子洲基坑工程为背景依托，结合监测数据和有限元模型探讨了双排桩结构的变形和受力机理，在较广泛应用的理正双排桩模型和新规范双排桩模型的基础上，研究并提出了更吻合实际的、适用于双排桩围护结构的修正设计计算模型，以更好地服务于工程实际。

图1　双排桩纵向剖面(单位：mm)

2工程概况

南京梅子洲基坑工程周围建筑物众多，为严格控制变形，部分区域采用双排桩围护结构。如图1所示，前桩长17.5 m，后桩长13 m，前、后排间距13 m。钢筋混凝土冠梁尺寸为1.4 m×1.0 m，钢筋混凝土连梁尺寸为0.8 m×1.0 m，前排桩后采用三轴搅拌桩止水帷幕。基坑悬臂开挖7.9 m，开挖前基坑降水至开挖面以下1 m处。

桩体结构主要涉及4层土，分别为杂填土①、淤泥质粉质黏土②、粉砂③以及粉细砂④。场地内地表以下10～13 m均为淤泥质粉质黏土，局部厚度达23 m。该地层以下以粉细砂为主，深度达50 m，之后进入强、中风化的泥岩地层。

3双排桩变形机理和结构受力研究

3.1有限元模型

基于连续介质理论的有限元法是目前解决工程领域数值计算最流行的计算方法[13-14]，在合理选择计算参数和本构模型的前提下，有限元法得到的计算结果具有很好的研究和参考价值。本文采用PLAXIS有限元软件，建立二维有限元模型，其中前桩和后桩按照抗弯刚度等效为地连墙，连梁等效为连板。有限元模型尺寸为100 m×50 m，左右边界水平位移约束，底边水平、竖直双向位移约束。

土体本构模型选用Harding-Soil(HS)模型，相较于Mohr-Coulomb模型，HS模型采用双曲线应力-应变关系，同时刚度模量不断变化的特性适用于具有典型卸载特色的基坑开挖过程。

结合该计算断面的现场监测位移数据，通过反演分析获得了表1所示的较合理的有限元地层计算参数。利用表1参数得到的有限元计算结果可以对双排桩结构的计算参数作进一步分析研究。

表1　土体参数计算值

3.2变形机理

为分析不同间距下双排桩的受力变形机理，分别计算前、后排桩间距为2、4、6 m和8 m的有限元模型，计算得出的前桩变形如表2所示。可知，双排桩整体侧向位移较小，控制变形能力强。桩间距为2～6 m时，桩顶位移即为桩身最大位移；桩间距为8 m时，最大位移位于桩顶以下，连梁的锚拉作用较为明显。综上，双排桩间距小时，整体性明显；桩间距大时，锚拉性明显。

表2　前桩位移值

双排桩结构主要受到桩身侧向土压力作用，通过有限元模型中的接触单元可计算出桩身侧向土压力值，为双排桩荷载结构模型的土压力荷载取值提供参考依据。

由于开挖面以上土压力对结构变形影响大，本文土压力研究主要针对开挖面以上桩体部分。前排桩有限元土压力计算值如表3所示。后排桩侧向土压力计算值如表4所示。

表3　前排桩外侧侧向土压力　kPa

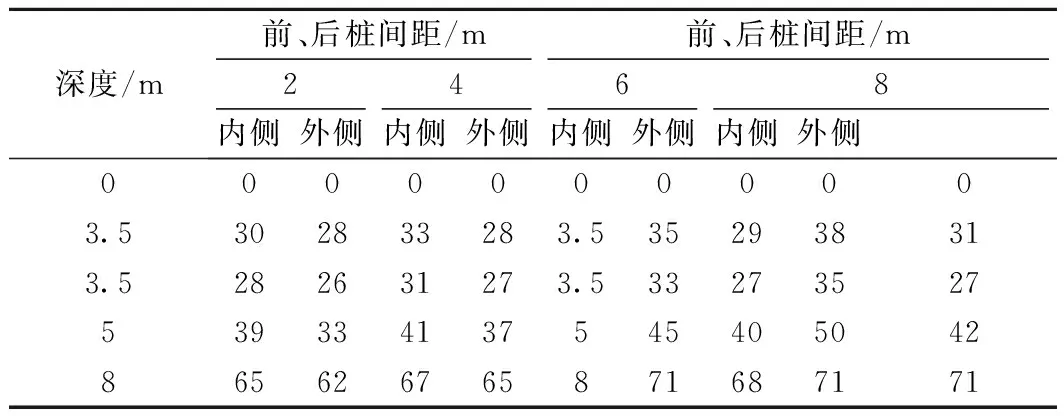
表4　后排桩侧向土压力　kPa

由表3可以看出，不同桩间距下前排桩侧向土压力值相差较小，说明前、后桩间距对前桩土压力影响很小。桩身上部位移大，土压力偏向主动土压力；桩身中下部位移小，土压力偏向静止土压力。侧向土压力总体处于主动和静止土压力之间。

由表4可以看出，桩身上部位移大，土压力偏于主动，桩身中下部位移小，土压力偏于静止。内侧与外侧侧向土压力值相差不大，总体内侧值略大。表明后排桩通过桩间土体将侧向土压力传递给前排桩。

4与常用双排桩计算模型的对比分析研究

4.1理正模型

该模型根据土体积比例系数法[5，15]理论进行分析，即前排桩土压力按开挖面确定，后排桩土压力按等效开挖面确定。该方法在理正软件中得到了实现和推广应用，如图2所示，此处暂将其称为理正模型。

图2　理正模型

理正模型表明前、后排桩共同承担土压力，并通过土压力分配系数进行分配。开挖面和等效开挖面以下采用接地弹簧模拟土体抗力，其中：

前桩土压力

(1)

后桩土压力

(2)

(3)

(4)

式中，ea为作用于桩身土压力，kPa。

水平地基基床系数

(5)

式中m——水平基床系数比例系数，kN/ m4；

z——计算点距开挖面距离，m。

4.2新规范模型

图3　新规范模型

《建筑基坑技术规程》(JGJ120—2012)中对双排桩结构建议采用如图3所示的平面刚架模型计算[1]。

后排桩外侧作用主动土压力；

前排桩嵌固段土反力

(6)

前、后排桩的桩间土体对桩侧压力

(7)

(8)

式中ps0——初始土反力强度，kPa；

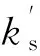
Δv——前、后桩相对位移，减小为正值，增大为零，mm；

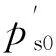
Sy——双排桩排距，m；

d——桩径，m。

4.3计算结果对比分析

本次研究分别令前、后排桩间距为2、4、6 m和8 m，理正模型、新规范模型和有限元模型的计算结果见图4～图6。

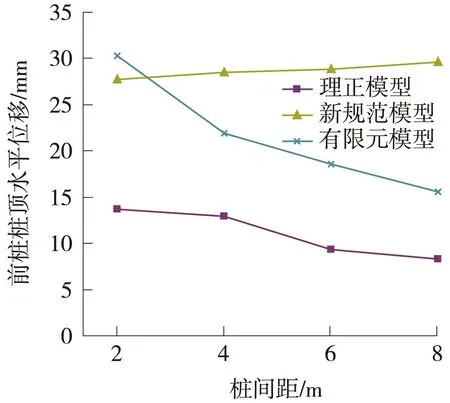
图4　前排桩桩顶水平位移

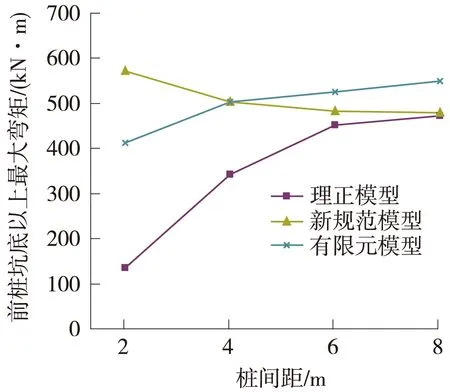
图5　前排桩坑底以上最大弯矩

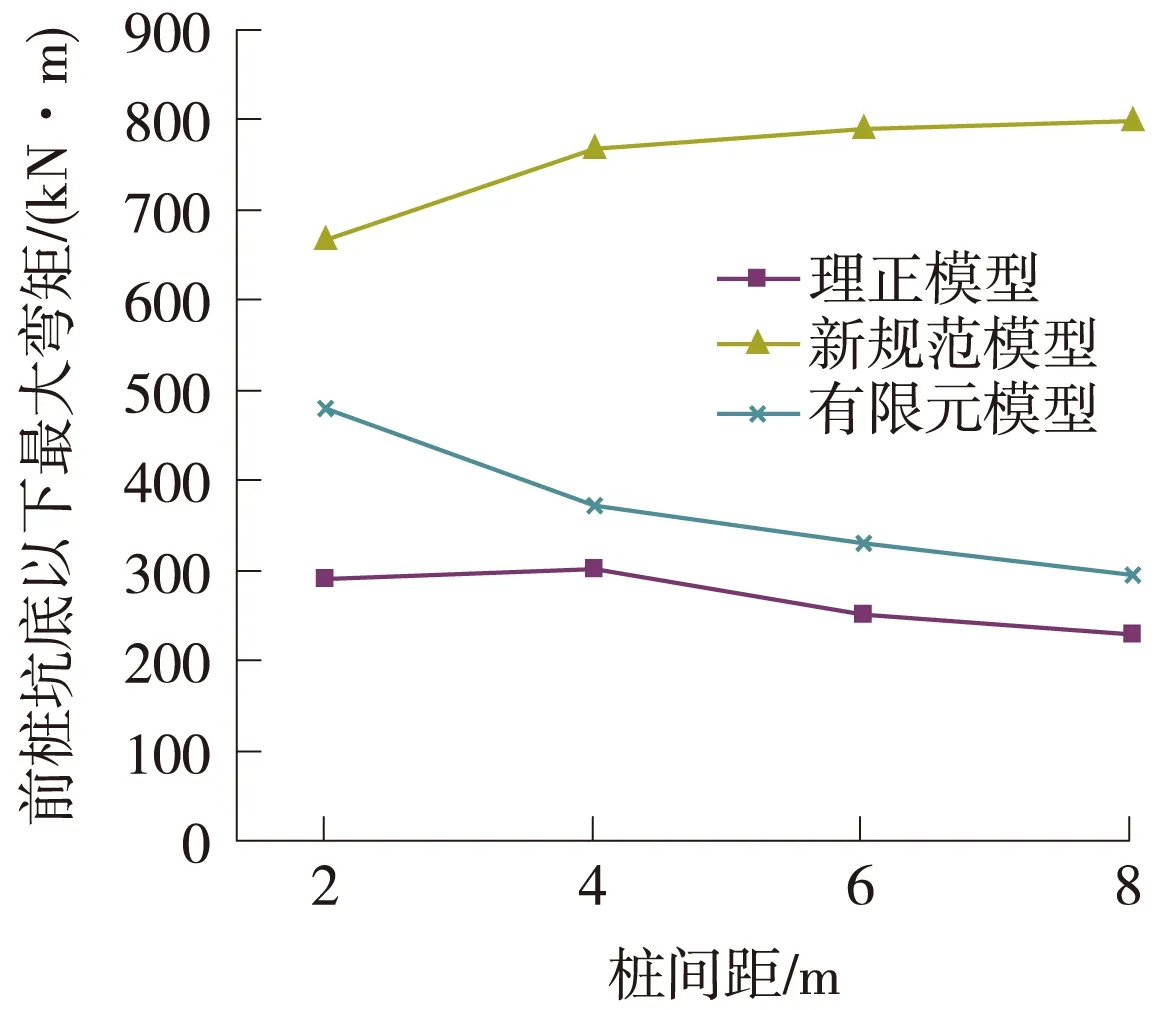
图6　前排桩坑底以下最大弯矩

图4表明，理正模型与有限元模型的位移计算结果变化规律一致，但理正结果整体偏小。新规范模型中位移随桩间距增大而增大，与实际不太符合。

图5、图6表明理正模型计算的结构内力与有限元模型计算结果变化趋势一致，但桩间距为2～4 m时偏差较大。新规范模型内力计算结果与有限元相差较大。

综上，从变形机理和结构受力的角度而言，理正模型与基于监测数据的有限元模型计算结果比较接近，可针对理正模型进行修正。

5修正的双排桩设计计算模型

5.1土压力修正

通过有限元模型计算可知(表3、表4)，前桩承担所有主动土压力，后桩内侧土压力较外侧大。双排桩荷载结构模型中可将土压力全部作用于前桩，后桩不作用土压力荷载，本次研究据此结论对土压力进行修正。

5.2嵌固段弹簧刚度修正

基坑围护结构嵌固段水平地基基床系数K常采用“m”法计算。其中最为常见的两种刚度取值是三角形分布与梯形分布。

三角形

(9)

梯形

(10)

沿海地区土质较软，根据多个工程实际经验，梯形分布临界深度约5 m左右。

以桩间距4 m的双排桩为例，计算上述两种刚度取值模式下的结构变形和内力，如表5所示。

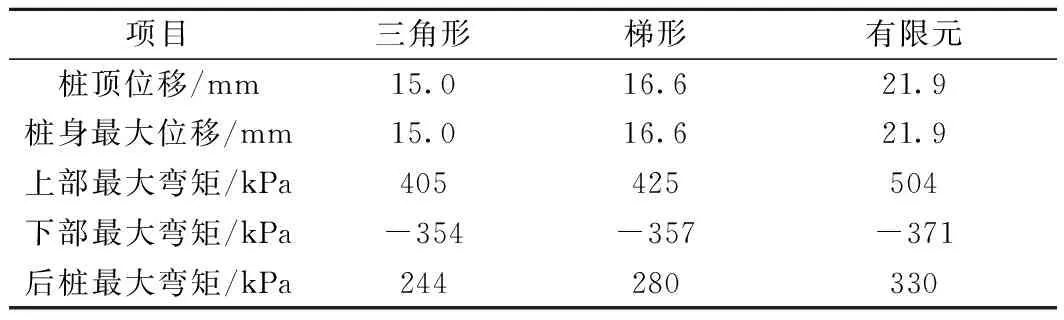
表5　桩间距4 m时计算值

由表5可知，从变形和内力的角度而言，梯形弹簧刚度取值法与有限元模型计算结果更加吻合；三角形取值法会使得嵌固段土体刚度较大，结构变形较小。

5.3后桩内侧弹簧刚度折减修正

理正模型采用的接地弹簧边界与新规范模型采用的桩间连接弹簧是两种模型间最本质的区别。前面的计算结果表明采用接地弹簧更符合结构变形和受力特性，但桩间土体本质上是有限空间土体，采用接地弹簧边界模拟对后排桩的限制作用会造成土抗力过大，与实际不符。可针对不同前、后排桩间距双排桩模型，计算出合理的后排桩内侧弹簧刚度折减系数ω。

经过多次计算，合理的后排桩弹簧刚度折减系数ω如表6所示。

表6　不同桩间距的ω

5.4双排桩修正模型

结合前述研究，基于理正计算模型，本文对土压力、嵌固段弹簧刚度取值以及后桩内侧弹簧刚度折减等进行了修正，提出了相应的更符合实际的“双排桩修正模型”。

双排桩修正模型、理正模型、有限元模型的计算值对比如图7～图9所示。结果表明，双排桩修正模型的计算结果从变形规律和数值大小方面相比于理正模型，更加吻合基于监测值的有限元模型，适用于普通间距的双排桩围护结构。

图7　前排桩桩顶水平位移

图8　前排桩坑底以上最大弯矩

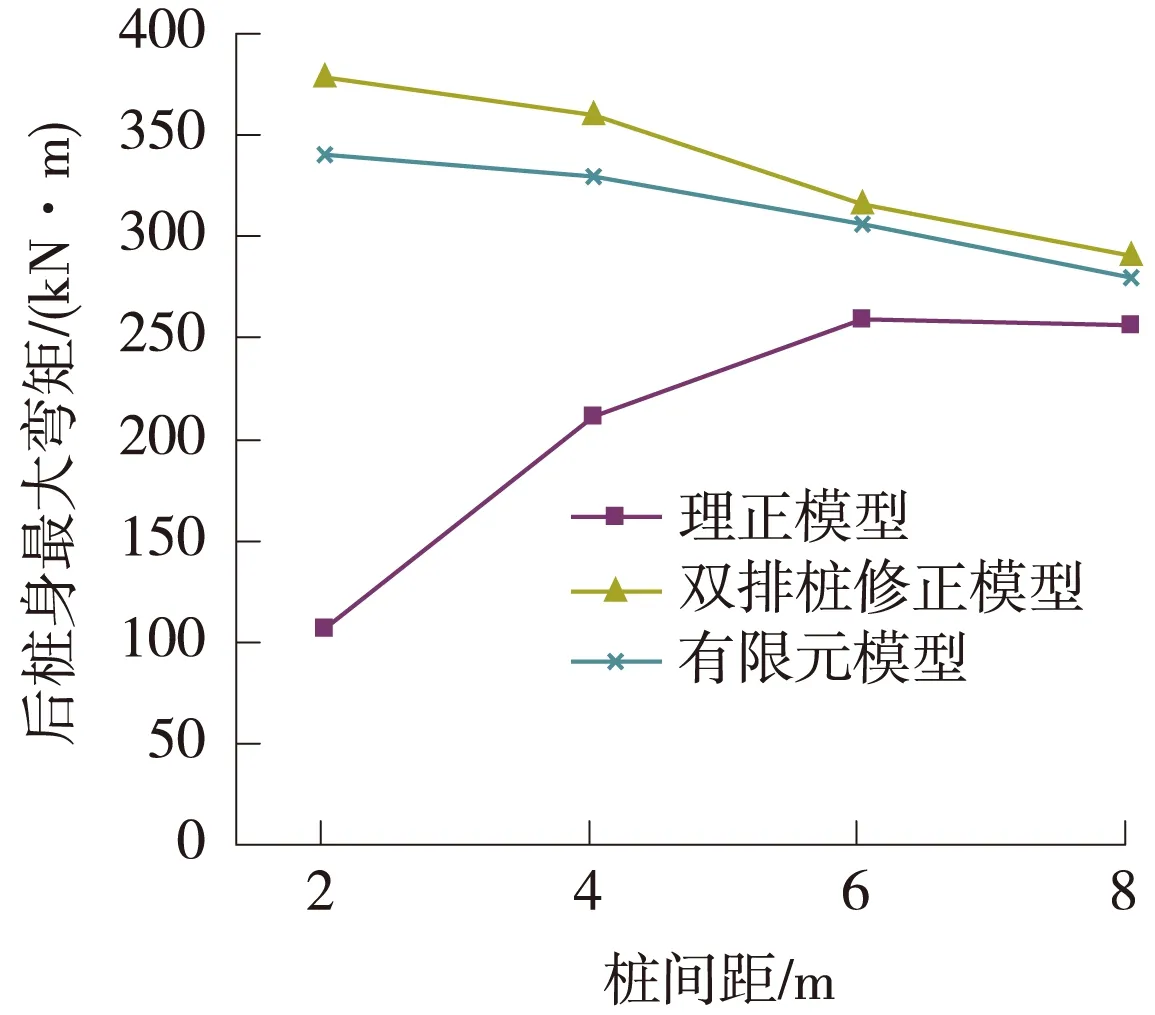
图9　后排桩桩身最大弯矩

6结论

本文首先结合监测数据，通过有限元模型计算对双排桩结构受力和变形机理进行研究；在此基础上，结合理正模型、新规范模型和有限元模型的对比分析研究，提出了新的双排桩修正计算模型。主要得出以下结论。

(1)有限元模型计算结果表明：双排桩控制变形能力强。桩间距较小时，体现整体性；桩间距较大时，体现锚拉性。前桩外侧土压力整体介于主动土压力和静止土压力之间；后桩内侧土压力较外侧稍大。

(2)理正模型、新规范模型和有限元模型计算结果表明：理正模型的变形和内力变化趋势和有限元较为接近，新规范模型部分规律不符合有限元模型，可针对理正模型进行修正。

(3)将理正模型中土压力进行修正，即前桩开挖面以上外侧承担全部主动土压力，开挖面以下为矩形土压力荷载；后桩外侧不承担土压力。通过计算表明，修正土压力符合双排桩受力变形特性。

(4)嵌固段弹簧刚度采用“m”法计算时，梯形分布比三角形分布的计算结果更符合双排桩结构特性。

(5)后桩内侧弹簧采取刚度折减时，可使计算结果更为准确。一般前、后桩间距为2～8 m时，折减系数为0.2～0.5。

(6)双排桩修正模型能够较好地反映结构变形和力学特性，模型简单，易于实际工程设计应用。

参考文献：

[1]中华人民共和国住房和城乡建设部.JGJ120—2012建筑基坑支护技术规程[S].北京：中国建筑工业出版社，2012.

[2]张勉，薛光桥，蔡永昌.拉锚式双排桩荷载结构模型计算研究[C]∥中国建筑业协会深基础施工分会，中国土木工程学会土力学及岩土工程分会桩基础学术委员会，中国工程机械学会桩工机械分会.第五届全国深基础工程发展论坛会议论文集，2015:41-46.

[3]张弘.深基坑开挖中双排支护结构的应用与探讨[J].地基处理，1993，4(3):42-47.

[4]林栋.用双排灌注桩作深基坑围护结构的尝试[J].建筑施工，1994(4):18-19.

[5]何颐华，杨斌，金宝森，等.双排护坡桩试验与计算的研究[J].建筑结构学报，1996(2):58-66.

[6]熊巨华.一类双排桩支护结构的简化计算方法[J].勘察科学技术，1999(2):32-34.

[7]郑刚，李欣，刘畅，等.考虑桩土相互作用的双排桩分析[J].建筑结构学报，2004(1):99-106.

[8]刘钊.双排支护桩结构的分析及试验研究[J].岩土工程学报，1992(5):76-80.

[9]程知言，裘慰伦，张可能，等.双排桩支护结构设计计算方法探讨[J].地质与勘探，2001(2):88-90，93.

[10]戴智敏，阳凯凯.深基坑双排桩支护结构体系受力分析与计算[J].信阳师范学院学报：自然科学版，2002(3):348-352.

[11]蔡海兵，黄以春，李阳.基于随机介质理论的土体融沉预测及其参数敏感性分析[J].铁道标准设计，2015(8):107-111.

[12]侯新宇，刘松玉，童立元.主、被动土压区加固对地铁深基坑变形影响的数值分析[J].铁道标准设计，2012(4):94-97.

[13]焦苍，范鹏，徐成家.深基坑支护结构变形预测研究与应用[J].铁道标准设计，2005(1):81-84.

[14]孙毅，戴李春，齐俊，等.深浅式异形基坑开挖工法比选与地表沉降特点研究[J].铁道标准设计，2015(9):125-129.

[15]旷庆华.同深基坑开挖引起紧邻地铁车站变形特性研究[J].铁道标准设计，2015(5):130-132.

收稿日期：2015-11-11； 修回日期：2016-01-04

作者简介：薛光桥(1979—)，男，高级工程师，2005年毕业于武汉理工大学结构工程系，工学硕士，E-mail：21987532@qq.com。

文章编号：1004-2954(2016)07-0116-05

中图分类号：U452

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2016.07.027

Research on Mechanism and Computation Model of Deep Foundation Pit Double-row Pile Structure

XUE Guang-qiao1，2

(1.China Railway Siyuan Survey and Design Group Co.， Ltd.， Wuhan 430000， China;2.Hubei Provincial Engineering Laboratory for Underwater Tunnel， Wuhan 430000， China)

Abstract：In recent years， the double-row piles structure is widely promoted and applied in deep foundation pit to meet the needs of intensive and complicated underground projects due to its high lateral stiffness， less deformation and quick construction and the vigorous development of urban underground engineering construction. However， in practical design， there is no unified design method and there exists a certain degree of conservative due to the lack of standard theory to match the structure deformation mechanism with calculation models. With Nanjing Meizizhou Qingao city underground space engineering program and field monitoring data， the deformation mechanism and soil pressure distribution law of double-row pile retaining structure are studied， which is gradually promoted and used in underground engineering field in recent years with finite element computation model. On the basis of this， a practical and reasonable corrected computation model of double-row pile retaining structure is recommended after the comparison and analysis of the widely used Lizheng and Xinguifang double-row pile models. This model structure is featured by clearness， high accuracy， and practical application in engineering design. The model can be easily applied in computation and analysis of double-row pile structure．

Key words：Deep foundation pit; Double-row pile; Deformation mechanism; Computation model; Finite element method