有限元极限平衡法在黄土边坡稳定性分析中的应用探讨

王　月，叶朝良

(石家庄铁道大学土木工程学院，石家庄　050043)



有限元极限平衡法在黄土边坡稳定性分析中的应用探讨

王月，叶朝良

(石家庄铁道大学土木工程学院，石家庄050043)

摘要：对目前边坡稳定分析中的极限平衡和有限元两类方法进行分析阐述，在此基础上，结合黄土边坡工程算例，利用geostudio软件将有限元与极限平衡法相结合进行黄土边坡稳定性分析，并对其计算结果进行比较。算例分析结果表明：极限平衡法在求解过程中作出各种假定来解决超静定问题；有限元法克服了极限平衡法的不足，考虑土体的本构关系，但不能确定可能破裂面，对边坡失稳破坏的判断没有一个定量的标准，将有限元法和极限平衡法相结合，取长补短，既能反映边坡的稳定和变形之间的关系，准确描绘出破坏面的特征，又能得到更精准可靠的安全系数；有限元极限平衡法可自动搜索出坡肩带有垂直裂缝的组合滑动面，比极限平衡法搜索出的单一圆弧滑动面更贴近实际情况，提高了边坡稳定性分析的合理性，为类似边坡稳定性分析方法提供参考。

关键词：黄土边坡；极限平衡法；有限元；稳定性分析；裂缝

黄土是地球上分布广泛且性质特殊的一种沉积物，其结构疏松，具有垂直节理。近年来，随着黄土地区的工程建设规模不断扩大，经常会遇到黄土边坡的防护和治理等问题。黄土边坡在失稳之前，常常在坡顶出现张拉裂缝，其失稳破坏情况比一般边坡更加复杂，因此，找出一种适用于黄土边坡的边坡稳定性分析方法是十分必要的。

目前，边坡稳定性计算方法主要有极限平衡法和有限元法， 但各自在应用中存在一些问题。极限平衡法可以满足力和力矩的平衡，摩尔-库仑破坏准则和应力边界条件，其方法简单，概念清楚，因此在工程中被广泛应用。但其未考虑土体本身的应力-应变关系和实际的工作状态，所得的安全系数只是假定滑裂面上的平均安全度，求出的条间力和滑条底部反力并不是真实数值，没有考虑边坡失稳的破坏机理。有限单元法是目前在边坡稳定评价中应用最广泛的数值方法。但是，这类数值方法没有给出一个明确的稳定性安全系数以及可能的破坏面，限制了其在工程中的应用。

近年来许多学者尝试将两种方法相结合并取得了一定的成果，曾亚武，田伟明[1]将有限元分析计算的应力结果通过应力张量变换的方法，求得滑动面上的应力分布，然后通过积分或求和的方法来求解对应滑面稳定性安全系数。杨辉[2]在有限元法分析应力的基础上将稳定性分析问题转化为带有约束条件的数学规划问题，可以描述为：设定安全系数Fs为目标函数，利用有限数目的坐标节点(xi，yi)将曲线v离散，在已知应力场内，给定一组坐标点的x坐标，变化寻找相应的y坐标，使其所确定的曲线v对应的安全系数为最小。巩留杰[3]根据模型同一高度塑性应变特点寻找滑裂面，输出滑裂面上节点主应力σx、σy、τxy，然后计算滑裂面上总的正应力、切应力，进而计算安全系数，本文所采用的有限元极限平衡法通过限元法分析计算岩土体内较为真实的应力分布，采用插值方法得到已给定滑动面上的应力值，然后结合极限平衡法的概念得出边坡的稳定性安全系数，结合黄土边坡的具体实例进行分析，对不同方法的优缺点进行了分析研究。

1常用边坡稳定性分析方法

1.1极限平衡法

极限平衡法假设土条为刚体，依据纯粹的静力学原理，即力的平衡方程和力矩的平衡以及摩尔-库仑强度准则来判断边坡的稳定性。极限平衡法不涉及应变和位移，没有考虑位移的兼容性，因而不可能获得真实的应力分布，这一缺点造成的该方法的局限性。

极限平衡条分法采用了简化假定的方法，减少了未知量的数目，表1总结了常用的几种极限平衡条分法的条间力假定及主要特征。极限平衡法的详细内容见文献[4]。

表1　典型极限平衡法的条间力假设及主要特征

1.2有限元法

有限元法将土体离散化成有限个通过节点相互联系的单元，按照弹塑性理论，得出土体的应力应变关系，可以解决各种加荷历史和地质条件复杂的边坡问题。近年来国内外很多学者运用有限元法对边坡进行稳定性分析[5-12]，发现尽管该方法有其自身的优越性但也存在一定的弊端。该方法常常把塑性区的贯通作为判别边坡失稳的判据，但很多工程实例证明塑性区出现贯通边坡并不一定失稳。而有限元强度折减法通常把计算不收敛作为边坡失稳的判据，这种情况下迭代方法和收敛容差的选取对计算结果产生了很大的影响。有限元法对边坡失稳并没有一个明确的判断标准，是塑性区的贯通还是计算不收敛，将有限元法和极限平衡法相结合，以安全系数作为边坡失稳的判据，很好地弥补了有限元法的缺点。

1.3有限元极限平衡法

边坡失稳从根本上说是由于各种因素引起了坡体内部应力和强度的变化，所以边坡的稳定性与其应力状态密切相关。本文采用的有限元极限平衡法通过有限元计算输出模型区域内真实应力场分布，采用插值方法得到假定滑动面上的应力值，依据下述公式计算沿滑动面的安全系数，进而在真实的应力场中得到确定的最危险滑动面，不需要对条间作用力做任何假定，通过有限元法计算出应力场，不存在迭代和收敛问题，易于工程中的推广和应用。以传统的极限平衡法为基础使该方法更具有说服力，极限平衡法虽然并不精确，但其具有悠久的历史，经过了多年的使用和观察校准，这种可信度是一种完全新的方法所不能提供的。

有限元极限平衡法依据 Mohr-Coulomb 强度准则确定土体中任意一点的土体抗剪强度，滑动面安全系数Fs定义为沿滑动面土体抗剪强度与实际剪应力的比值

通过弹塑性有限元分析，计算出对于每个单元高斯积分点的σx、σy、τxy，进而利用差值函数求出各土条中点的σx、σy、τxy，用摩尔圆来计算土条底部的正应力和剪切力，按照上述公式计算Fs值，重复上述处理直到第n个土条。

2工程应用

2.1工程概况

选取位于陇西地区的天然黄土边坡为例，考虑不同分析方法，对其进行边坡稳定性评价。工程所在地区属于中温带半干旱大陆性气候，干旱少雨，黄土边坡坡高20 m，坡面倾角56.4°，坡面平整，土质均匀，为砂质黄土，可将该斜坡简化为如下计算模型：土体采用莫尔-库仑理想弹塑性模型，模型底部采用刚性边界，材料参数：容重γ=18.5 kN/m3，弹性模量E=45 MPa，v=0. 3，黏聚力c=16.0 kPa，内摩擦角27°，该边坡为老黄土单一结构边坡，分析过程不考虑地下水的影响。

2.2计算结果对比分析

采用geostudio程序，通过有限元SIGMA/W模块，计算出应力状态，将结果导入边坡SLOPE/W模块，计算得出滑坡的潜在滑动面及安全系数，实现有限元法和极限平衡法的结合。

2.2.1最危险滑裂面形状

有限元的计算模型如图1所示，限定模型两侧的水平位移和模型底部两个方向的位移，采用四边形和三角形单元划分网格，该有限元模型共划分301个单元，包含337个节点。

为了便于分析边坡坡顶处的变形情况，分别提取坡顶处(截面aa)、19 m处(截面bb)、18 m处(截面cc)、17 m处(截面dd)、16 m处(截面ee)截面上各点的水平方向应力值、应变值和各截面处的剪应力值，见图2～图4。由图2可以看出，坡顶处和19 m处截面水平向应力的变化趋势明显区别于其他三截面处，应力值先逐渐增大，在水平位置为18 m附近，水平应力值达到峰值，而后又迅速减小。由此可推断，在水平位置为18 m左右的坡肩附近有可能产生裂缝，而18 m处截面的水平应力虽然也在水平位置18 m附近达到峰值，但其曲线较为平缓，应力值没有发生较大的变化。17、16 m截面处水平应力曲线并没有较为明显的峰值出现，由此可见，裂缝的开展在边坡坡顶截面(aa)和18 m处截面(cc)之间，即坡肩裂缝的深度在2 m之内。

图2　各截面水平应力分布情况

图3　各截面水平应变分布情况

图4　各截面的剪应力分布情况

图3中坡顶截面和19 m截面处的水平向应变在水平位置18 m附近出现峰值，说明该位置处的土体发生了较大的拉伸变形，进而可推断水平位置18 m附近是坡顶裂缝最可能出现的地带。同时从图中可以发现18、17、16 m截面处的应变曲线较为平缓，并没有明显的峰值出现，且全部为负值，说明坡顶竖向裂缝的开展不会到达18 m截面处，与前面的论证相符。

各截面的剪应力分布如图4所示，从该图中可以得到如下两个推断：(1)所取5个截面的剪应力均在18 m附近发生正负的改变，剪应力的方向发生变化，其位置与边坡上部的最大拉应力区一致。说明边坡在该区域内易发生剪切破坏；(2)坡顶截面处和19 m截面处的剪应力曲线与x轴的交点基本上是重合的，即坡顶截面和19 m截面处的剪应力是在同一水平位置达到零值，发生方向的改变，据此可以推断，至少在距离坡顶1 m内，断裂是垂直开展的。这与前面的分析一致，说明了该边坡的破坏会在坡肩处形成垂直裂缝，且裂缝的水平位置在18 m附近，而裂缝的竖向开展范围在坡顶截面(aa)与18 m处截面(cc)之间。

利用geostudio软件分别用有限元极限平衡法和传统的极限平衡法(Morgenstern-Price法、Bishop法、Ordinary条分法和Bishop)对该边坡进行稳定性分析，发现用有限元极限平衡法得到的滑裂面在坡肩的地方呈垂直划裂状，其滑面为垂直裂隙面与圆弧面组合形成的滑裂面，如图5所示，裂缝的水平坐标为18.1，且裂缝的开展范围在坡顶截面(aa)与18 m处截面(cc)之间，与之前的推断相符。而4种极限平衡法所找到的最危险滑动面的形状和位置基本一致，呈简单圆弧状。

图5　滑动面形状对比

极限平衡法假设土条为刚体，用分析刚体的办法来分析土体，且对条间力的作用做了各种假设，其计算出的滑动面上的应力状态显然是不真实的。因此在某些情况下极限平衡法得出的最危险滑动面的位置有所偏差，而有限元法极限平衡法将土坡当成变形体，搜索出的滑动面形状更接近真实状态。基于有限元的边坡稳定性分析方法考虑了土体的本构关系以及变形对应力的影响，基于土体内真实的应力状态搜索最危险滑裂面，得到的滑裂面在坡肩呈垂直滑裂状态，坡肩裂缝的形成减少了划弧的长度，裂缝不断加深与圆弧滑动面相交，形成由圆弧面和垂直裂隙面共同组成的滑动面。裂缝的形成是一个需要从地质和力学的角度综合考虑的复杂问题，极限平衡法只是简单地将土条视为刚体，通过静力学平衡方程求解，只得到简单的圆弧状的滑裂面，而无法得到坡肩部分由张拉破坏产生的直立的裂缝，显然与实际情况存在出入。

常规的极限平衡法不能得到真实的滑裂面形状，针对这种情况，部分学者对常规的极限平衡法进行修正，得到了考虑裂缝的极限平衡法，该方法认为，若在受力分析中出现了拉应力则认为是裂缝，进而搜索最危险的裂缝，在最危险裂缝处与圆弧滑裂面相交。该方法存在如下两个问题：(1)在搜索滑裂面之前，是否考虑裂缝需要人为的分析并进行选择，而在有限元极限平衡法中，不需要分析是否考虑裂缝，基于土体内真实应力状态的分析搜索最危险滑裂面，这是一个自动化的过程，所判定的最危险滑裂面的形状位置真实可靠；(2)极限平衡法本身对条间力引入了各种假定，求出的条间力和滑条底部反力并不是真实数值，由土条的受力出现拉应力来判断裂缝位置，是不准确的。由常规极限平衡法、考虑裂缝的极限平衡法和有限元极限平衡法这3种方法得到的滑裂面的形状位置如图6所示。从该图可以看出，考虑裂缝的极限平衡法搜索出的滑动面为垂直裂缝加圆弧形，其中圆弧段与未考虑裂缝的极限平衡法所搜索出的圆弧滑动面基本上是重合的。而采用有限元极限平衡法所得到的裂缝位置与采用考虑裂缝的极限平衡法时十分接近，说明采用有限元极限平衡法得到的裂缝位置是可靠的。

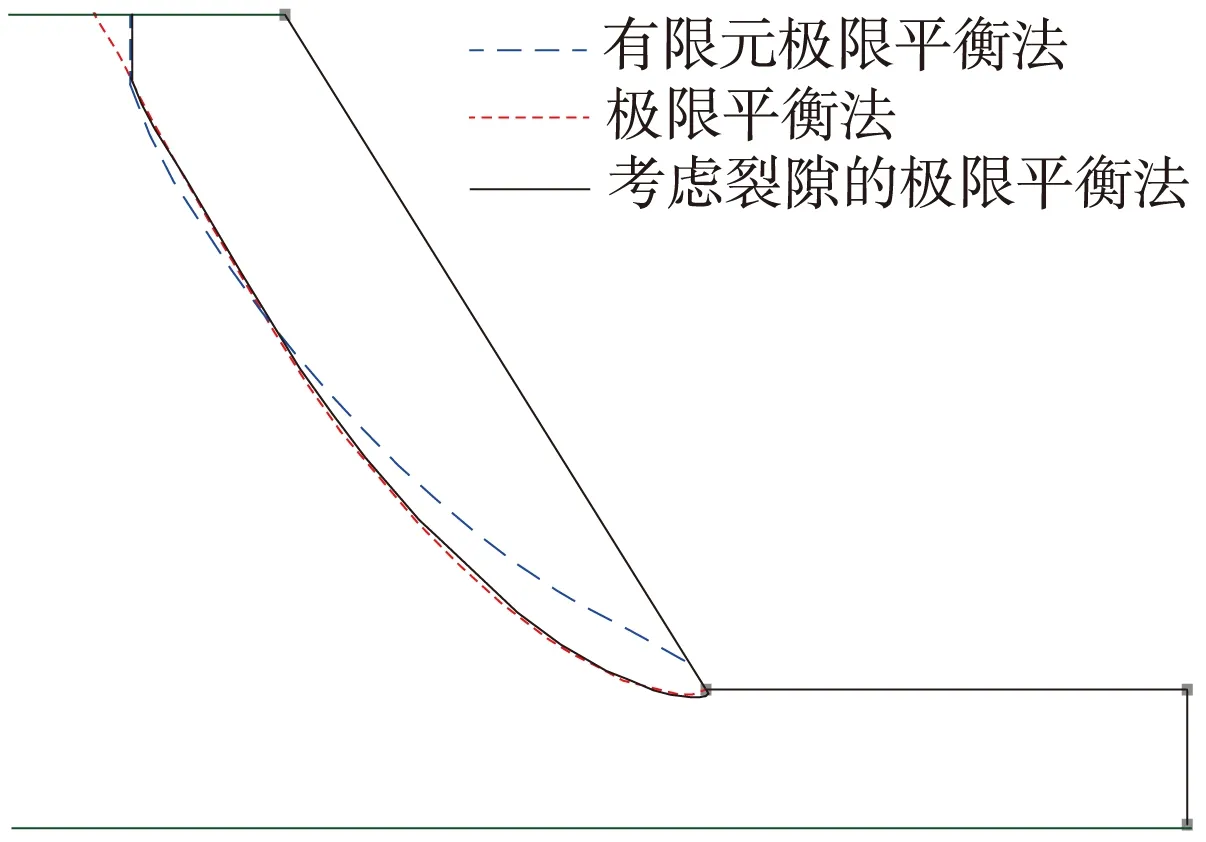
图6　不同方法的滑裂面位置对比

2.2.2稳定性安全系数

极限平衡方法之间的区别在于条块间相互作用力的大小和方向的假定不同，其中普通条分法假定条块间的作用力为零，因此计算误差较大。Morgenstern-Price法和Bishop法所得的结果比较相近，且相比于其他条分法结果更为准确。

Janbu法硬性规定了土条侧向力作用点的绝对位置，迭代过程不能灵活调整，当条块数量太多、条块宽度太小时，计算结果往往不收敛。普通条分法不考虑条块间作用力，引起了较大的误差 ， 使结果偏小。在实际工程中不建议采取这两种方法。

Morgenstern-Price法得到的边坡安全系数较大，收敛较好。其原因是它在静力平衡要求、滑裂面的形状以及多余未知数的迭代各方面均不做任何假定，能较好反映出最危险滑面各土条间相互作用力的情况，Morgenstern-Price法是计算任意形状滑动面安全系数最为严谨的一种条分法。

利用有限元应力结果计算得的安全系数为1.149，比各种条分法算得安全系数都有所提高，最大相差14%(普通条分法)，最小相差10%(Bishop法)，比考虑裂缝的极限平衡法最大相差17%，最小相差10%。在实际工程中，利用极限平衡法得到安全系数低于规范时，边坡往往还处于稳定状态，计算结果和实际情况存在偏差。安全系数产生差异的原因是沿滑裂面上应力的分布不同。图7为条间力为一恒定函数的Morgenstern-Price法、有限元法、考虑裂隙的极限平衡法得到的正应力分布对比图，由该图可以得出如下结论。(1)水平位置17～18 m处采用极限平衡法时滑动面上存在拉应力，而考虑裂隙的极限平衡法则认为在此段产生裂缝，进而搜索出最危险裂缝在水平位置18 m处，边坡由此开裂，此处正应力为零。而在18～30 m处，采用考虑裂隙的极限平衡法时滑动面上的正应力与采用极限平衡法是基本相同，故采用这两种方法搜索到的圆弧滑裂段的形状位置是相同的。(2)坡趾区有限元极限平衡法得到的正应力大于极限平衡法，在以有限元为基础的分析方法中很好地体现出了边坡坡趾的剪应力集中现象，而极限 平衡法中正应力源自于土条的重力，无法反映出应力集中现象。有限元极限平衡法考虑了土体的本构关系，以及变形对应力的影响，得到的滑动面形状和滑弧位置更贴和实际情况。

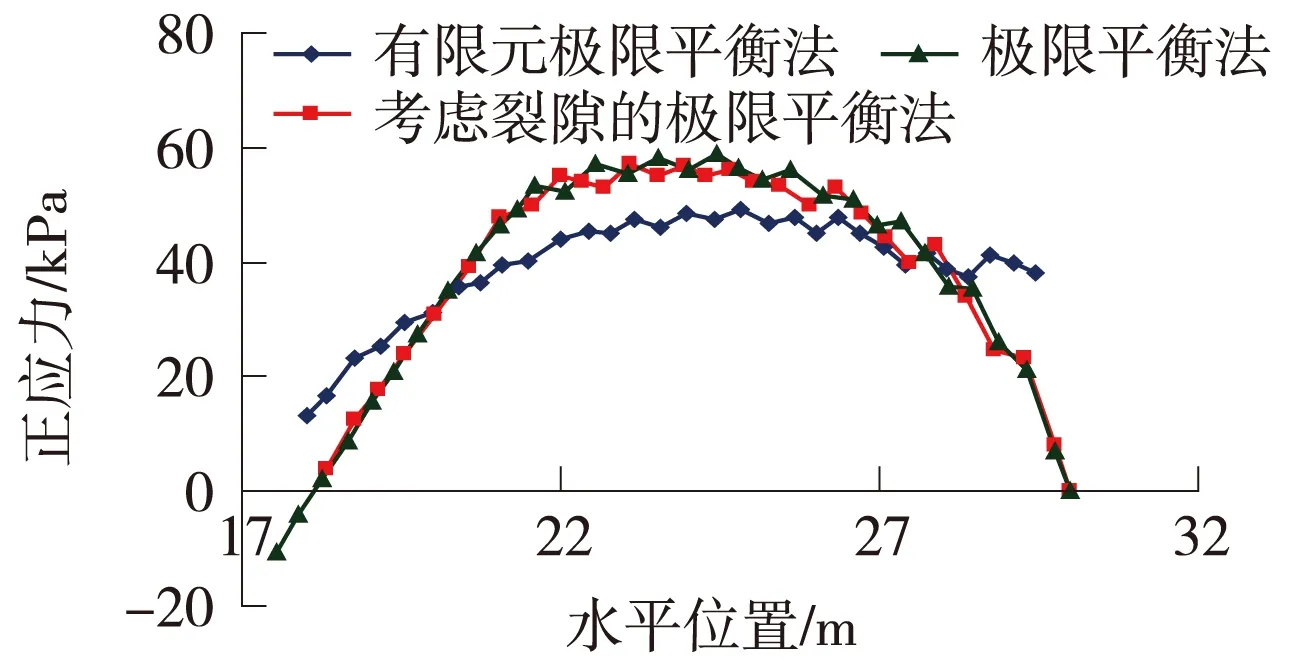
图7　滑裂面上的正应力分布

另外，从表2中可看出，采用Bishop法进行计算时，裂缝的存在对安全系数并无影响，而采用Janbu法时，裂缝的存在使安全系数降低了4.07%。进一步计算分析表明，采用Bishop法进行边坡稳定性计算时，裂缝对安全系数的影响是及其微小的，这显然与实际情况不相符，而采用Janbu法考虑裂缝时，安全系数降低的最为显著，故Bishop法不适用于黄土边坡的稳定性分析。

由图8可看出，边坡坡趾存在应力集中现象，剪应力沿潜在滑动面方向逐渐增大，尤其是坡脚部位剪应力较大，当其剪切应力超过了该点的抗剪强度，则该点产生剪切破坏，随着滑坡体滑动的逐步发展，潜在滑动面上发生应力重分配，破坏点逐步增多进而形成连续破坏面。垂直方向上的应力分布中值得注意的一点为，应力等值线的轮廓并不是一个恒定的厚度，如图9所示，应力为80 kPa的等值线在坡趾处发生突变，一部分轮廓厚度明显减小，这意味着垂直方向上的应力不仅受重力的影响，也受到剪切应力的影响。

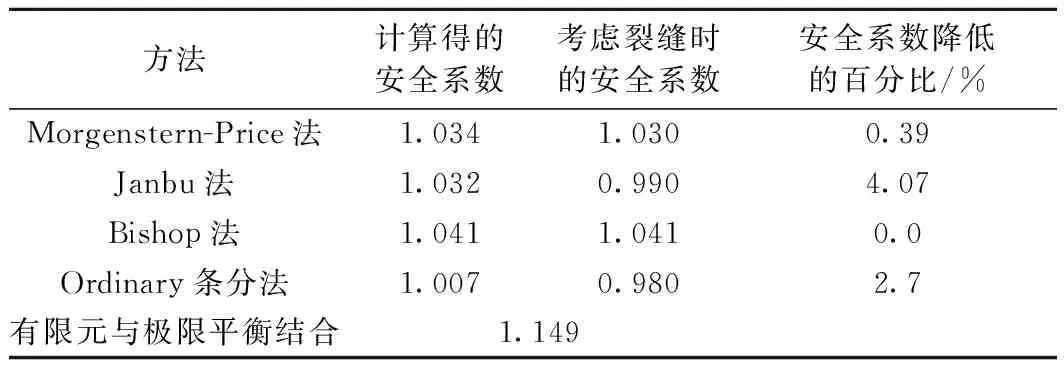
表2　安全系数计算结果

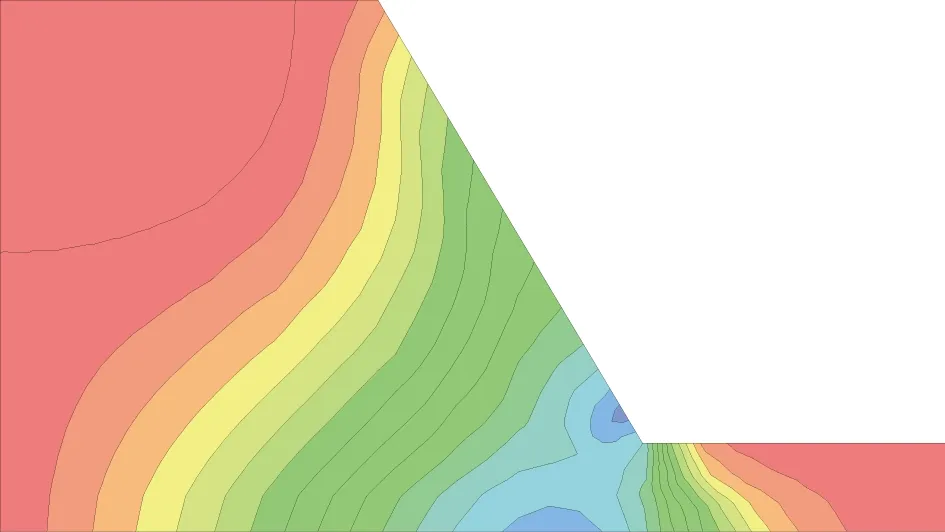
图8　剪应力分布

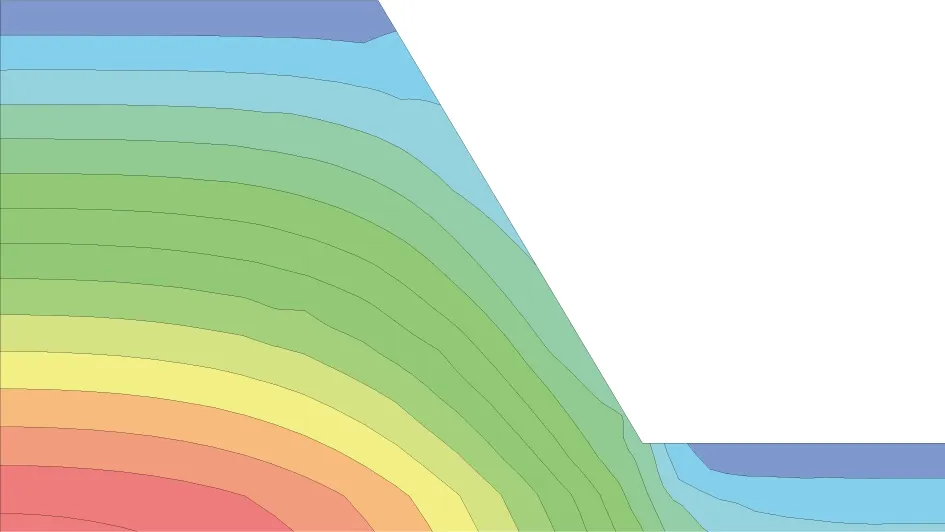
图9　垂直向应力分布

3结论与建议

通过对边坡稳定性分析方法的分析总结，并结合工程算例的计算分析，得到如下结论和建议。

(1)针对具有特殊破坏面形状的黄土边坡，建议有限元极限平衡法将更具可靠性。对于节理发育的黄土边坡，传统的极限平衡法无法真实地反映坡肩裂缝的形成，而有限元极限平衡法自动搜索出了由垂直裂隙面和圆弧面共同组成的最危险滑裂面，更贴近现实中黄土边坡滑动面的形状。

(2)有限元极限平衡法与考虑裂隙的极限平衡法所得到的裂缝位置十分接近，且其计算的安全系数提高了大约10%，说明采用有限元极限平衡法进行黄土边坡稳定性分析的合理性和精确性。

参考文献：

[1]曾亚武，田伟明.边坡稳定性分析的有限元法与极限平衡法的结合[J].岩石力学与工程学报，2005(S2):5355-5359.

[2]杨辉.边坡稳定分析的有限元极限平衡法原理及程序实现[D].北京：北京交通大学，2014.

[3]巩留杰.基于有限元计算的边坡稳定极限平衡法研究[D].长沙：湖南大学，2012.

[4]陈祖煜.土质边坡稳定分析：原理·方法·程序[M].北京：中国水利水电出版社，2003.

[5]孙聪，李春光，郑宏，等.同时考虑张拉及剪切破坏的边坡上限原理有限元法[J].岩石力学与工程学报，2015(S1):2783-2791.

[6]唐亚明，冯卫，李政国.黄土滑塌研究进展[J].地球科学进展，2015(1):26-36.

[7]汤连生，桑海涛，罗珍贵，等.土体抗拉张力学特性研究进展[J].地球科学进展，2015(3):297-309.

[8]迟世春，关立军.基于强度折减的拉格朗日差分方法分析土坡稳定性[J].岩土工程学报，2004(1):42-46.

[9]唐亚明.陕北黄土滑坡风险评价及监测预警技术方法研究[D].北京：中国地质大学，2012.

[10]段钊.黄土滑坡触发机理研究[D].西安：长安大学，2013.

[11]王振文.黄土深路堑边坡稳定性分析及边坡坡型的合理设计[J].铁道标准设计，2013(4):17-20.

[12]李守升.某黄土边坡滑塌机理分析及治理方案研究[J].铁道标准设计，2014(S1):70-72.

收稿日期：2015-10-13； 修回日期：2015-12-21

基金项目：国家自然基金项目(50978172)；铁道部科技研究开发计划项目(2010G018-B-4)

作者简介：王月(1991—)，女,硕士研究生，E-mail：1296739730@qq.com。

文章编号：1004-2954(2016)07-0038-05

中图分类号：U213.1+3

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2016.07.009

Application of Finite Element Limit Equilibrium Method in Stability Analysis of Loess Slope

WANG Yue， YE Chao-liang

(College of Civil Engineering， Shijiazhuang Tiedao University， Shijiazhuang 050043， China)

Abstract：The limit equilibrium and finite element methods for slope stability analysis are analyzed. On the basic of it， the limit equilibrium method based on the finite element stress field is analyzed by using GeoStudio software with reference to the engineering calculation of loess slope. The example analysis results show that the limit equilibrium method in solving process has made various assumptions to solve the statically indeterminate problem; the finite element method can overcome the deficiency of the limit equilibrium method in consideration of the constitutive relationship， but can not determine potential rupture surface. There is no quantitative criterion for judging the failure of slope. The combination of the finite element method with the limit equilibrium method can not only reflect the relationship between slope stability and deformation but also accurately depict the failure surface features with more accurate and reliable safety factor. The limit equilibrium method based on the finite element stress field can automatically search for the combined sliding surface with vertical cracks on the slope shoulder， which is much closer to the actual situation than the single arc sliding surface obtained with the limit equilibrium method. Thus the rationality of the slope stability analysis is improved to provide references for similar slope stability analysis．

Key words：Loess slope; Limit equilibrium method; Finite element method; Stability analysis; Cracks