步态能量图和KFDA的步态识别研究

王　竣，王修晖

(中国计量大学 信息工程学院，浙江 杭州 310018)



步态能量图和KFDA的步态识别研究

王竣，王修晖

(中国计量大学 信息工程学院，浙江 杭州 310018)

【摘要】为了有效地获取步态连续性的动态特征，快速准确地进行身份识别.特提出了一个基于步态能量图(Gait Energy Image,GEI)和核Fisher判别分析(Kernel-based Fisher Discrimination Analysis,KFDA)的分类识别算法.算法首先以步态能量图(GEI)按列向量作为输入，求得最优子空间Wopt和αopt.利用提取步态能量图(GEI)的步态信息向量计算在αopt上的投影，并计算其投影轨迹.在分类阶段，采用最近邻分类器(Nearest neighbor classifier).最终在中科院自动化研究所CASIA B步态数据库上进行实验，对比多项式、高斯径向基核函数和其他四种算法的结果显示，本文算法取得了较高的识别率.

【关键词】步态能量图；核Fisher判别分析；多项式核函数；高斯径向基核函数

近些年，随着计算机视觉领域和生物特征识别的发展，步态识别作为一种新的生物特征认证技术，受到了研究者们密切的关注.步态识别旨在通过人的走路姿势来进行身份识别，相比于其他生物特征(如指纹、掌纹、人脸等)，其优势在于可以远距离进行识别，具有非接触性、非侵犯性、不易被察觉、难于隐藏和伪装的特点，因此被广泛应用在门禁系统、医疗诊断、安全监控等领域.

步态识别由运动检测、特征提取和特征识别三个阶段所组成.步态特征提取方法对于识别结果会有一定程度的影响，通常分为两类:基于构建人体模型的方法和基于非模型的方法.基于构建人体模型的方法将人体按生理特征进行建模，如YOO[1]等构建的摆角模型、Cunado[2]等建立的钟摆模型、URTASUN[3]等建立的3D运动模型.采用构建人体模型的方法通常需要获取轮廓清晰的步态序列，缺点在于对步态序列的质量要求高，构建模型的时间复杂度高.而基于非模型的方法主要考虑人的运动情况，主要提取人体目标移动时的侧影图形状.如KALE[4]等将人体步态轮廓宽度作为步态特征，SARKAR[5]等提取了步态的侧影序列作为特征.

HAN[6]等人在2005年将步态能量图(GEI)应用到步态识别中，取得了较好的识别效果.步态能量图定义为一个步态序列周期内的平均侧影轮廓图像.由于步态能量图在计算过程中的随机噪声被抑制，因此步态能量图具有较强的鲁棒性，节省了存储空间和计算时间.近些年的研究中，基于核函数的Fisher判别分析(KFDA)方法已被广泛地应用到模式识别中.KFDA已在人脸识别领域取得了比其他方法(如PCA,FLD,KPCA)更好的识别效果,文献[7]通过对比GKFD(KFDA)和其他几种方法(PCA、FLD、PCA+KFDA)的误识率，实验结果表明KFDA方法的误识率是最低的.本文以步态能量图作为步态特征，采用基于核函数的Fisher判别分析(KFDA)方法进行分类，在识别阶段采用最近邻分类器.本文算法实验结果表明，利用步态能量图的列向量作为步态特征，并采用KFDA的分类方法取得了较高的识别率，并且对于衣着的遮挡具有鲁棒性.

1步态序列预处理和周期检测

在实际步态序列采集过程中，由于存在干扰因素的影响，所以在步态特征提取前需要对采集到的视频序列进行处理.

由于采集环境中的步态序列背景是相对不变的，因此可以对背景进行建模，建模后采用背景减除法对人体轮廓进行提取,通常用当前步态帧与建模后的背景帧相减，得到的差值再与与事先给定的阈值比较，大于阈值的帧作为人体轮廓，小于阈值的帧则为背景,相减后对图像进行二值化处理，得到初始的步态轮廓图.基于初始的步态轮廓图，利用形态学腐蚀和膨胀算法消除噪声和阴影，对像素点连通性进行分析，选择最大的像素连通域作为人体步态轮廓.

本文针对二值化得到的步态轮廓图进行归一化处理，降低计算的时间复杂度和多余的信息，因此将240×240的步态图像归一化为64×64.

由于本文主要对特征提取和分类进行研究，所以对于步态周期的选取采用常用的方法，即考虑侧影图像帧的宽度和高度比周期性的变化，在两次宽高比最大值出现时的时间差可以将其作为一个步态周期.

2步态能量图

获取有效的步态特征对于步态识别具有重要的意义，但由于步态特征隐藏在行走阶段，包括人行走的频率、脚踝变化、摆臂姿势等，仅从一幅步态帧提取特征并不能准确地体现步态之间的相关性，所以通常需要进行周期性的步态序列提取.而在实际处理过程中，提取周期性的步态序列帧会导致计算的复杂度过大，考虑到选取步态特征时既要考虑减少步态图像的样本数，又要尽可能多的保留步态的主要特征.步态能量图较好地解决了上述问题，最早由HAN[6]等人提出，它的主要思想是利用加权平均算法将一个步态周期的图像合成一张图像，这幅图像保留了原始步态轮廓的相位和步态频率信息.步态能量图反映了一个步态周期内的累积能量图，像素的亮度值反映了身体在此位置出现的频率(能量).

给定步态序列的侧影轮廓图像Bt(x,y)，步态能量图(Gait Energy Image,GEI)的定义如下:

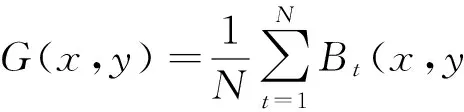
(1)

式(1)中，N表示一个步态周期的帧数；t代表帧数；x,y代表图像中二维平面坐标值；Bt(x,y)代表第t帧图像在点(x,y)的像素值.一个步态周期内90°视角下的步态能量图如图1.

图1　正常行走时不同视角下的步态能量图Figure 1　GEI of different views under normally walking

图2　一个人90°视角下三种状态下的步态能量图Figure 2　GEI of three conditions under the view of 90°

3核Fisher判别分析方法

3.1核函数定义

核函数方法定义为:通过非线性变换φ(x)，将随机矢量x映射到高维的特征空间F中.即:x→φ(x)∈F.核函数因其将线性方法推广到非线性方法，在实际应用中具有重要的意义.

3.2Fisher线性鉴别分析

线性鉴别分析算法主要基于Fisher准则.Fisher准则函数定义如下:

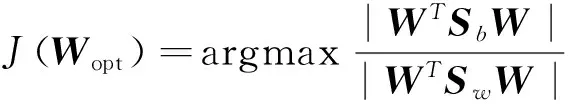
(2)

其中，Sb、Sw、St表示类间、类内离散度和总体样本的散度矩阵(协方差矩阵)，三者定义如下:

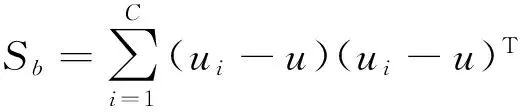
(3)

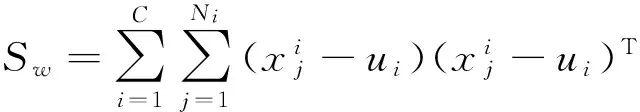
(4)

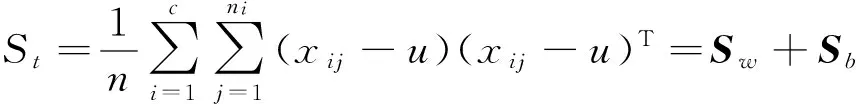
(5)

其中，C表示类别数，Ni是Ci类的样本数，u表示样本向量均值，ui是Ci类样本均值，xji是Ci类中的第j个样本.

Fisher线性鉴别分析算法的核心思想是求得最优的投影矩阵Wopt，目的是使在低维空间里类别相异的样本最大可能的分离，同类样本最大可能的聚集，以测试样本在矩阵Wopt上的投影作为鉴别特征，从而进行识别.

3.3基于核函数的Fisher判别法

假设有n个样本{x1,x2,…,xn}隶属于c类{X1,X2,…,Xc}中的一类.根据Fisher线性鉴别分析，非线性函数φ(x)将n个样本数据映射到特征空间F中，可以得到最优子空间Wopt.

=[w1,w2,…,wm].

(6)

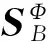
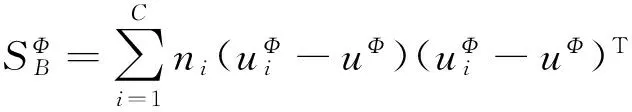
(7)

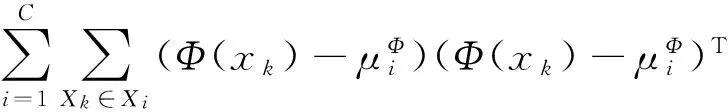
(8)

其中，

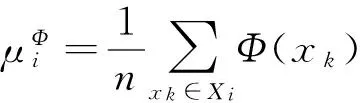
(9)

(10)

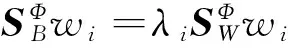
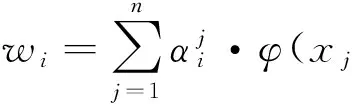
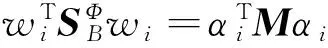
(11)

其中，

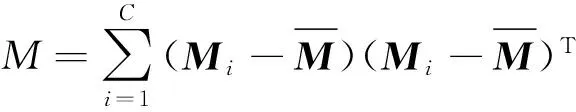
(12)

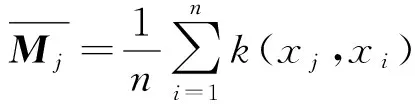
(13)

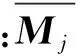
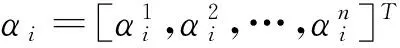
(14)

同样地，(6)式的分母可以改写为

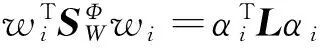
(15)

其中，

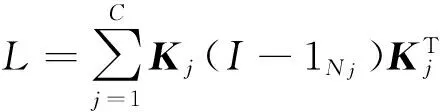
(16)

Kj为n×nj矩阵，并且，

(Kj)nm=k(xn,xm),xm∈Xj.

(17)

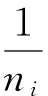
通过将(6)式的分子和分母化简，(6)式可以表示为

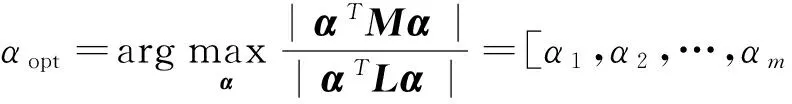
(18)

最优子空间Wopt为

Wopt=[w1,w2,…,wm]=

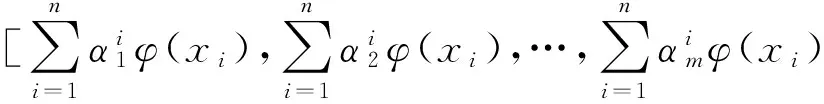
(19)

当给定非线性映射函数φ(x)，样本x在特征空间F上的映射结果为

φ(x)Wopt=

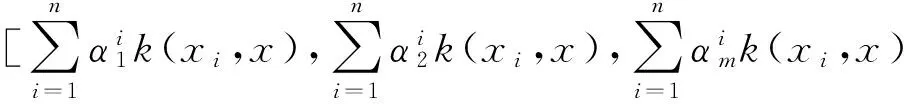
(20)

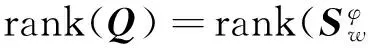
4基于GEI的核Fisher判别分析

假设有m个人，每个人对应于不同角度下的步态序列.本文算法提取每一个人的步态能量图(GEI)所包含的步态信息组成向量作为输入样本.

考虑到步态序列中的样本数为mi，i=1,2,…,q,样本集为{x1,1,x1,2,…,x1,n1,x2,1,…,x2,n2,…,xq,nq}，输入样本n=n1+n2+…+nq.

步态序列的训练和分类算法流程如下:

1) 计算K(x,y)：因为特征空间F的维数较高，为了在特征空间F上运用Fisher线性判别分析方法，通常使用内积核函数近似运算，即

K(x,y)=φ(x)·φ(y)

(21)

通过核函数，在特征空间F中，向量φ(x)和φ(y)的内积可以替换为x和y的内积.

2) 计算类间离散度矩阵Sb和类内离散度矩阵Sw.

3) 计算αopt.

4)将一个步态序列的步态能量图映射到最优特征空间Wopt,获得步态序列在Wopt上的轨迹.

5) 在训练阶段已求得Wopt，把GEI映射到Wopt中，得到训练特征Train Features(T1,T2,…,Tu).在测试阶段，把步态序列的步态能量图(GEI)映射到最优特征空间Wopt中，得到测试特征Test Features(t1,t2,…,tv).利用两者之间的欧式距离(Euclidean Distance)度量训练和测试序列的相似度，从而进行分类.对于训练集Tx(x=1,2,…,u)与测试集ty(y=1,2,…,v)之间的欧式距离定义为

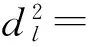
(22)

使dl最小值对应的第l类则为测试步态序列隶属的类，即它被分类到离它最近样本所属的类中.

6) 计算识别率.

5实验与结果分析

5.1步态数据库

为了验证本文算法的识别效果，采用中国科学院自动化研究所提供的CASIA Dataset B(多视角库)数据库上进行实验，实验环境为Matlab 2014a.

Dataset B数据库是一个拥有124个人、11个视角，(0°，18°，36°，…，180°)的步态数据库，有正常，穿大衣，携带包裹三种状态的步态序列.在同一个视角下有10个视频，其中包含6个正常步态序列(A)，两个携带包裹序列(B)和两个穿大衣序列(C).

5.2实验过程

步态检测和跟踪主要针对步态图像进行检测步态序列每个人的侧影图，依据侧影图进行轮廓的提取.本文主要研究的重点是特征提取和分类，因此，对于如何获得人体轮廓的过程不展开分析，采用CASIA数据库里面的人体侧影图提取特征和识别.由于步态能量图(GEI)是一个步态周期内侧影图平均得到的，也是时间归一化得到的累积能量图.我们把每一个人的步态能量图按列向量展开作为输入样本，在特征训练阶段，选取不同角度下的前一半序列作为测试样本，剩余样本进行测试.在计算完样本之后，采用核函数的Fisher判别分析方法对特征进行训练，得到αopt和最优特征空间Wopt.当得到αopt和Wopt之后，将样本向量在最优特征空间Wopt上投影,分别得到训练特征Train_Features和测试特征Test_Features.在分类识别阶段，将测试样本在特征空间上投影，计算测试序列和训练序列之间的欧式距离，将测试归为与它距离最小的训练样本所属的类.

5.3识别结果与分析

5.3.1实验结果

实验1数据库采用CASIA B库，该库中总共124人，在11个视角下(0°，18°,36°，…，180°)采集，选取正常状态下的步态序列在每一视角下的前3组图像作为训练集，剩余的3组图像作为测试集，其训练样本数为372，测试样本数为372,见表1和表2.

表1　实验1中不同核函数的识别率

表2　实验1中不同核函数的识别时间

实验2实验选取90°视角下的3组正常状态，1组背包状态和1组穿大衣状态下的步态能量图作为训练集，训练集样本数为620.测试集选取3组正常状态，1组背包状态和1组穿大衣状态，测试集样本数也为620.见表3.

表3实验2中不同核函数的识别率和识别所需时间

Table 3Identification rate of five algorithms in experiment 2

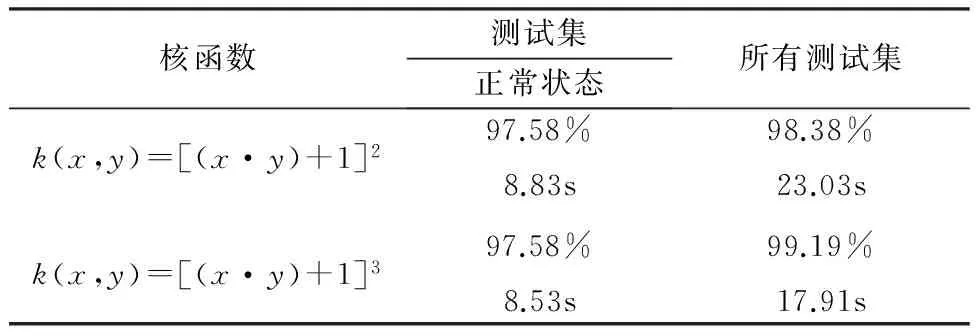
核函数测试集正常状态所有测试集k(x,y)=[(x·y)+1]297.58%8.83s98.38%23.03sk(x,y)=[(x·y)+1]397.58%8.53s99.19%17.91s

实验3数据库采用CASIA B库，该库中总共124人，在11个视角下(0°，18°，36°，…，180°)采集，实验选取正常状态下的步态序列在每一视角下的前3组图像作为训练集，剩余的3组图像作为测试集，其训练样本数为372，测试样本数为372.见表4.

5.3.2结果分析

在分类识别中引入正确分类率CCR(Correct Classification Rate)作为一种合理的评价指标.在测试集中，将测试样本Ti输入到训练集得到的k个分类器，Ci输出唯一的+1，其他输出-1，则成功地识别出Ci,正确分类率CCR定义为

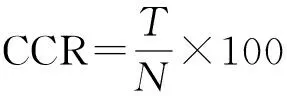
(24)

其中T表示正确识别的样本数，N表示总测试样本数.

表4　实验3中五种方法的识别率

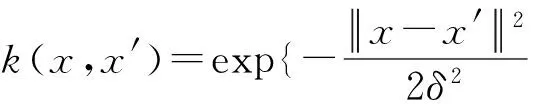
由于在实验1中对比了多项式核函数和高斯核函数的识别率，多项式核函数的识别率明显优于高斯核函数，所以在实验2中只对多项式核函数进行了识别率的验证.

在应用核Fisher判别法进行特征提取时，向量矩阵αk是由向量空间α的k个按递减顺序排列的特征值所对应的特征向量所组成.从表1可以看出，当选择多项式核函数时，由于CASIA中同一个人在正常状态下行走的步态序列有6组，即类别数为6.当降维至5时，选取5个按递减顺序特征值对应的特征向量，此时的识别率均在95%以上.考虑到本方法选取k-1个大于零按递减顺序对应的特征向量αopt=αk-1,α为n×n维，样本数n>>k-1，在用α计算样本x在特征空间F上的映射结果时，需要n2次乘法运算和n×(n-1)次加法运算，时间复杂度为O(n2)；而用αopt计算时，则只需要n×(k-1)次乘法运算和(n-1)×(k-1)次加法运算，时间复杂度为O(n)，节省了分类识别所需的时间.实验2在选取训练集考虑了正常行走、背包和穿大衣的情况，实验结果表明在选取多项式核函数进行识别时取得了较高的识别率.实验3对比了PCA(主成分分析法)，KPCA(核主成分分析法)，KSPP(核稀疏保留投影法)，PCA+SPP(主成分分析法和稀疏保留投影法)，KFDA(本文算法)五种方法的识别率.在本文实验中，高斯核函数在KPCA中为σ2=0.1，在KSPP中为σ2=0.02.从表1中看出，KPCA和PCA识别率相比，因为核函数参数设置唯一，导致在某些视角上提高了识别率，某些视角上降低了识别率.将主成分分析法和稀疏保留投影相结合，对于识别率较低的视角下取得了提升，主要因为稀疏保留投影方法计算得到的系数矩阵在保留最大稀疏度的同时也保留了原始数据的局部信息，使得特征具有更好的可分性.而通过基于KFDA的方法，最终的识别率在每一个视角上都有提升，说明本文算法对于不同数据具有很高的稳定性.

由此可见，基于核Fisher判别分析法的步态识别方法在小样本步态数据集上是一种可行的方法.

6结语

步态识别作为一种快速发展的生物特征识别技术，近年来受到广泛关注.本文主要在步态特征提取和识别进行了研究.并通过实验验证了KFDA应用到步态识别的可行性，比较了针对不同的核函数进行步态识别的效果，本文算法有很强的应用价值.由于本文仅测试了多项式核函数和高斯径向基核函数，并且步态数据库都是小样本，在接下来的研究中将考虑上述因素，期望获得更好的研究成果.

【参考文献】

[1]YOOJH,NIXONMS,HARRISCJ,etal.Extractinghumangaitsignaturesbybodysegmentproperties[C]∥Image Analysis and Interpretation.[s.l.]:IEEE,2002:35-39.

[2]CUNADO D, NIXON M S, CARTER J N,et al. Using gait as a biometric, via phase-weighted magnitude spectra[C]∥International Conference on Audio-& Video-Based Biometric Person Authentication.Berlin: Springer-Verlag,1997:93-102.

[3]LU H, PLATANIOTIS K N, VENETSANOPOULOS A N,et al. A full-body layered deformable model for automatic model-based gait recognition[J]. Eurasip Journal on Advances in Signal Processing,2008(1):1-13.

[4]URTASUN R, FUA P. 3D Tracking for gait characterization and recognition[C]∥IEEE International Conference on Automatic Face and Gesture Recognition.Seoul：IEEE,2004:17-22.

[5]SARKAR S, PHILLIPS P J, LIU Z, et al. The human ID gait challenge problem: data sets, performance, and analysis[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence,2005,27(2):162-77.

[6]JU H, BIR B. Individual recognition using gait energy image.[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence,2006,28(2):316-322.

[7]GAO Wengao, JIANG Kang, YU Zhenhua. et al. Human face recognition using generalizd kernel fisher discriminant and wavelet transform [C]∥2006 IEEE International Conference on Information Acquisition. Shandong: IEEE,2006:1258-1262.

[8]SCHÖLKOPF B, SMOLA A, MÜLLER K, et al. Nonlinear component analysis as a kernel eigen value problem[J]. Neural Computation,1998,10(5):1299-1319.

[9]HOFMANN M, GEIGER J, BACHMANN S, et al. The TUM gait from audio, image and depth (GAID) database: multimodal recognition of subjects and traits[J]. Journal of Visual Communication & Image Representation,2014,25(1):195-206.

[10]JENSSEN R. Mean vector component analysis for visualization and clustering of nonnegative data[J]. IEEE Transactions on Neural Networks & Learning Systems,2013,24(10):1553-1564.

[11]BEN X, MENG W, YAN R, et al. An improved biometrics technique based on metric learning approach[J]. Neurocomputing,2012,97(1):44-51.

【文章编号】1004-1540(2016)02-0216-07

DOI:10.3969/j.issn.1004-1540.2016.02.016

【收稿日期】2016-03-06《中国计量学院学报》网址：zgjl.cbpt.cnki.net

【基金项目】国家自然科学基金资助项目(No.61303146).

【作者简介】王竣(1991-),男,吉林省吉林人,硕士研究生,主要研究方向为计算机图形学和计算机视觉. E-mail:846411409@qq.com 通信联系人：王修晖,男,副教授.E-mail: wangxiuhui@cjlu.edu.cn

【中图分类号】TP301.6

【文献标志码】A

Gait recognition based on GEI and KFDA

WANG Jun, WANG Xiuhui

(College of Information Engineering, China Jiliang University, Hangzhou 310018, China)

Abstract:To effectively captures the dynamic features of the gait and accelerate the authentication and identification, a novel gait recognition algorithm was presented and a gait recognition algorithm based on GEI (gait energy image) and KFDA (kernel-based fisher discrimination analysis) was introduced. Firstly, the vector of the gait energy image(GEI) was used as the input to get the optimal subspace Woptand αopt. Then the extracted GEI vectors were used to compute the projection on αoptwith its projected path calculated. The nearest neighbor classifier was used for the classification.This method was evaluated on the CASIA B gait database.The comparison of the polynomial, the Gaussian kernel function and other four algorithms shows that the proposed method can obtain stable classification and performs satisfactory recognition results.

Key words:gait energy image; kernel-based fisher discrimination analysis; polynomial kernel function; gauss radial basis kernel function